基于Ludwieg管的高超声速边界层转捩实验

黄冉冉, 司马学昊, 成江逸, 赵家权, 吴 杰

(华中科技大学航空航天学院, 湖北武汉 430074)

引 言

高超声速边界层转捩是空气动力学中的一个重要难题, 虽然相关研究持续在开展, 但是目前仍没准确可信的高超声速边界层转捩预测方法, 以评估高超声速飞行器在设计阶段的气动力和气动热, 影响了超声速及高超声速飞行器的气动、 控制和热防护设计. 至今为止, 针对高超声速边界层转捩的研究已经开展了近60年, 由于影响转捩的因素繁多, 目前对于高超声速边界层转捩还处于认识的过程中, 存在着诸多需要深入研究与解决的问题, 如感受性问题、 高温真实气体效应对转捩影响、 旁路转捩、 横流转捩控制等[1-5]. 传统研究超声速及高超声速转捩现象的方式主要包括数值模拟、 飞行试验和地面实验. 由于在高速流动下的特殊流动情况, 比如真实气体效应、 高温非平衡气体效应等, 已有的数值计算模型并不适用[6-7]. 因此, 实验测量成为了研究超声速及高超声速边界层转捩预测的主要手段. 其中,飞行试验可真实地模拟飞行环境, 可以获得更为可靠的实验数据, 但是开展该类试验存在极大风险, 且成本极其昂贵; 相比之下, 地面实验由于其成本较低, 成为更易被接受的研究方法.

但是, 常规超声速及高超声速风洞设备建设成本高昂, 风洞的运行和操作也较为复杂, 实验测量所需的各类仪器昂贵, 以上因素提高了科研机构开展超声速及高超声速实验空气动力学基础研究的门槛. 针对这一问题, 德国Ludwieg于1955年提出了Ludwieg管风洞的设计方案[8]. 相比于常规超声速及高超声速风洞, Ludwieg管风洞的建设成本仅为同Reynolds数下常规高超声速风洞的1/3甚至1/4, 根据布伦瑞克工业大学Radespiel等的估算, 一座试验段口径为0.5 m的Ludwieg管高超声速风洞的建造成本约为1×106美元[9]; 由于动力方面仅需使用电力间歇式地运行真空泵和空气压缩机, 该风洞的运行操作仅需1名实验人员即可, 故风洞单趟试车成本约为数美元甚至更低; 此外, Ludwieg管风洞的运行时间主要由膨胀波在储气段的折返时间决定, 与常规高超声速风洞的总压下降运行相比, 该过程可产生定常的驻点压力和温度; 同时, 由于无需复杂的控制阀门, 总压损失小, 该风洞的试验段可模拟的Reynolds数相比常规的下吹式风洞更高.

得益于上述优点, Ludwieg管风洞近些年在欧洲和美国得到了极大的应用. 根据Cummings等2012年的统计, 全世界在使用的Ludwieg管风洞大概有18座[10]. 加上目前美国、 韩国以及我国正在建设中的数座Ludwieg管高超声速风洞, 预期未来5年Ludwieg管式高超声速风洞将超过25座. 可见, Ludwieg管风洞可以作为一种成熟的实验平台, 适合用于高超声速空气动力学实验研究.

为了开展高超声速边界层转捩相关的基础实验研究, 推进高超声速边界层转捩的深入研究, 设计并建造了一座Mach 6高超声速Ludwieg管风洞. 本文首先论述了Mach 6 Ludwieg管高超声速风洞的气动设计, 重点阐述了该高超声速风洞的启动过程与运行状态; 之后, 通过纹影和Pitot探头对该风洞的静态和动态流场进行了标定, 测量并分析了风洞的自由来流压力脉动值; 最后, 基于该高超声速Ludwieg管风洞开展了7°半张角尖锥标模的转捩实验研究, 对不稳定波的发展和传播特征进行了分析.

1 Mach 6 Ludwieg管风洞设计

1.1 Ludwieg管风洞运行原理

常规Ludwieg管风洞由长直储气段、 快开阀、 Laval喷管、 试验段、 扩张段和真空罐组成[11], 其运行原理见图 1. 风洞启动前, 储气段内充入高温高压空气, 喷管及下游的部分则通过真空泵抽成了真空, 风洞的高低压区通过快开阀门分开. 在开启快速控制阀门的瞬间, 由于高低压形成的压差作用, 会产生一系列的非定常膨胀波系以当地声速向储气段的上游行进(OA和OB),CD段分别表示该膨胀波系的波头和波尾; 膨胀波系到达储气段的尾端后会反射回来(AE和BF); 当反射回来的膨胀波系到达快开阀附近时一个稳定的风洞运行状态结束, 快开阀也随之关闭. 在膨胀波系向储气段演化的同时, 高压气体迅速向低压部分行进演化, 通过Laval喷管进行膨胀扩张, 形成风洞的启动激波; 启动激波向下游驱动, 在试验段内形成高超声速稳定来流.

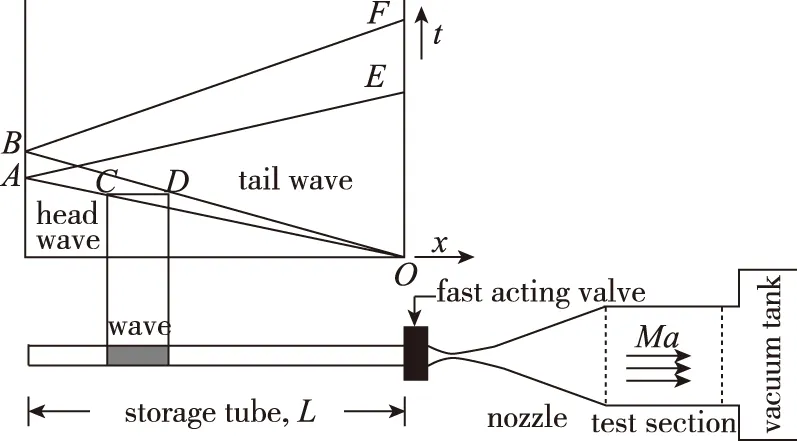
图1 Ludwieg式管风洞的运行原理图[11]Fig. 1 Mechanism of the Ludwieg tube tunnel[11]

1.2 Ludwieg管风洞设计

1.2.1 储气段设计

Ludwieg管风洞的有效运行时间可通过式(1)进行估算, 其中L表示管风洞长直储气段的长度,a为储气段内当地声速.

t=2L/a

(1)

为了开展高超声速边界层转捩等相关基础研究, 需要确保风洞有效运行时间达到100 ms以上. 受限于实验室的可用空间, 本风洞采用了储气弯管设计, 即3段直管通过2个U型管进行连接, 每段直管部分长6.5 m, U型管连接头的直径为0.4 m, 最终储气段的总长约为22 m, 可满足风洞100 ms以上的运行时间需求(储气段总温为443 K时对应104 ms, 总温为300 K时对应126 ms).

1.2.2 Laval喷管设计

Laval喷管是Ludwieg管风洞最重要的一个组成部分, 对整个风洞的流场质量起决定性作用. 典型的Laval喷管由收缩段、 喉道和扩张段组成, 本研究中收缩段采用3阶多项式生成; 喉道采用圆弧曲线以确保流动从亚声速流到超声速平缓过渡[12]; 扩张段采用Sivells特征线法(method of characteri-stic, MOC)生成[13], 中间存在一段线性段以抑制喷管壁面Görtler涡的发展. 综合考虑流场品质、 空间大小和制造成本等因素, 通过对收缩段和扩张段的长度进行优化, 以获得满足风洞整体设计要求的Laval喷管型线, 如图 2所示. 为了提高Ludwieg式管风洞的运行效率, 本风洞采用快开阀替代传统膜片, 并将快开阀安装在收缩段的上游, 以此隔开高压储气段和下游低压段.

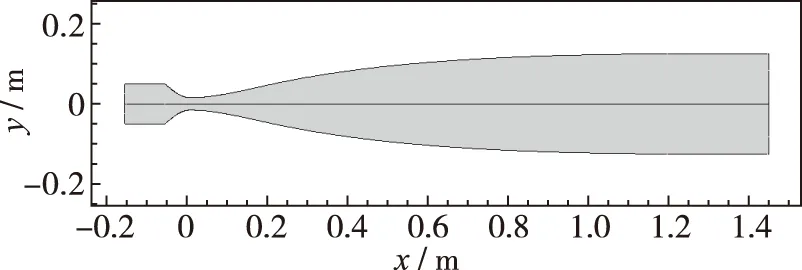
图2 华中科技大学Mach 6 Ludwieg管风洞Laval喷管型线Fig. 2 HUST Mach 6 Ludwieg tube(HLT) contour

1.3 风洞流场数值研究

1.3.1 数值方法

本文的数值计算为非定常模拟, 采用2阶有限体积求解器SU2[14-15], 其中湍流模型采用剪切应力输送(SST)模型[16-17], 对流项格式采用2阶迎风格式AUSM[18-19], 单步时间步长1×10-5s, 内迭代步数40步. 采用的计算网格如图 3所示, 为了考虑三维效应的影响和节省计算资源, 采用半模进行计算, 且全部采用结构化网格. 为了精确捕捉湍流边界层, 网格在壁面处进行加密,y+均取5; 储气段直线部分使用粗网格, 弯管部分采用相对致密网格, 以捕捉膨胀波特征, 整个模型网格总数为5.5×106个. 计算域边界条件定义如下: 风洞出口定义为压力出口[9]. 对称面采用对称边界, 壁面则采用绝热无滑移壁面边界条件.

图3 Ludwieg管半模网格Fig. 3 Half model grids of Ludwieg tube

对喷管流向和横向开展网格独立性验证. 横向的网格密度参考Wu等[20]的工作. 采用372×45, 442×55, 497×65, 502×75这4种不同的网格密度. 计算结果如图 4所示, 图中对4种不同网格密度下喷管出口切面的Mach数分布进行了比较. 可以看到当网格数为497×65时结果已不再明显变化, 网格密度满足计算需求.

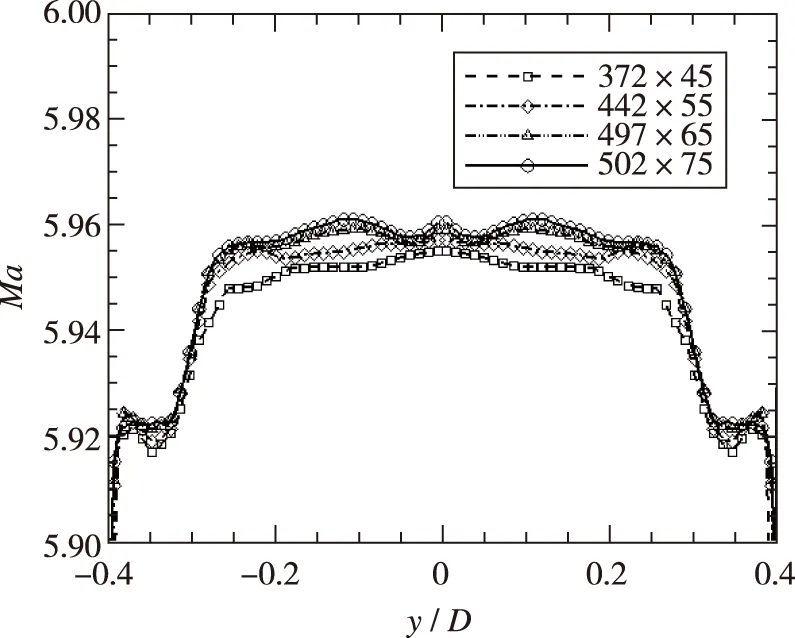
图4 网格独立性验证Fig. 4 Mesh independence verification

在进行数值研究之前根据已有文献对求解器进行验证, 以保证数值计算结果的可靠性. 本文以布伦瑞克Mach 6高超声速Ludwieg管风洞(hypersonic Ludwieg tube of Braunschweig， HLB)的喷管[9]为参考, 在相同网格密度和数值设置下, 使用SU2对HLB喷管进行了非定常数值模拟, 并将计算结果与文献中的数据进行了比较, 如图 5所示. SU2计算结果与Huang等[21]提供的DNS数据和DLR-TAU[9]程序计算的RANS结果符合得很好, 表明SU2对于高超声速Laval喷管的模拟结果是可靠的.

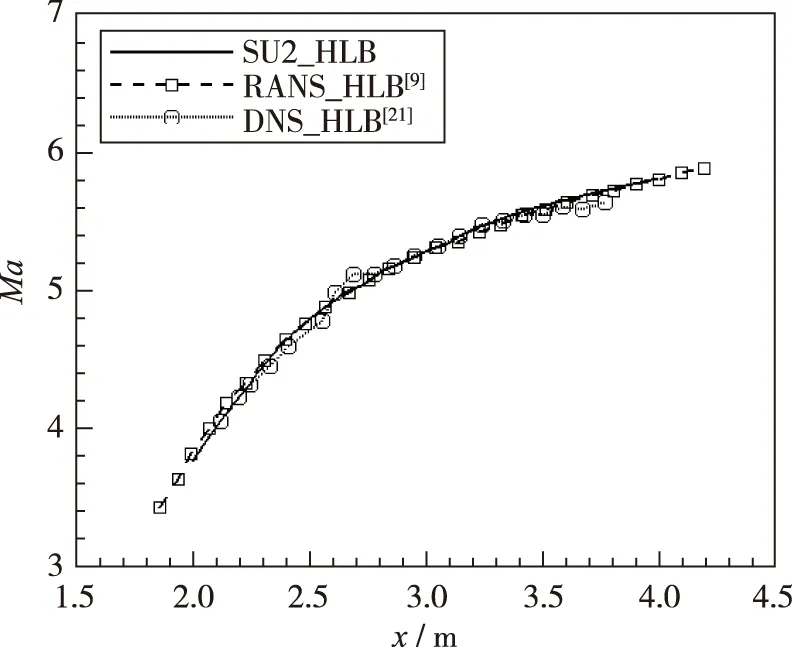
图5 不同数值求解器中心线Mach数的比较Fig. 5 Comparison of central line Mach number with different numerical solvers

1.3.2 风洞启动过程分析

对Ludwieg管风洞的启动过程进行了非定常模拟. 在快开阀与Laval喷管喉部的接触面上布置了一个数值膜片, 以初始化流场并进行时间瞬态模拟. 随着数值膜片的破裂, 风洞启动, 高压气流(P0=10 bar(1 MPa),T0=300 K)从储气段进入Laval喷管, 同时在喉道附近形成膨胀波. 如图 6所示, 在t=0.5 ms 时, 膨胀波以较高强度向上游传播, 高压气体向低压区驱动形成一道激波. 随着流动进一步发展到t=1.5 ms, 膨胀波通过快开阀, 而激波波头到达喷管出口. 到t=2 ms时, 激波消失在Laval喷管中, 膨胀波开始以恒定速度在储气段内传播, 此时试验段内已逐渐建立起稳定的高超声速流.

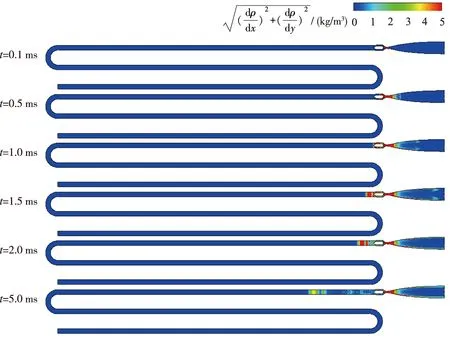
图6 Ludwieg管启动过程密度梯度云图Fig. 6 Density gradient contour for the starting process of Ludwieg tube

图 7给出了启动过程喷管出口处的Mach数分布, 可以看出Ludwieg管风洞在5 ms内便可建立起稳定的高超声速流动.

1.3.3 风洞运行流场分析

对稳定后的流场进行分析, 计算结果如图 8和图 9所示. 从Mach数分布结果可以看出, 加入快开阀后的喷管内依旧存在较大的试验匀流区, 其流向尺寸达0.5 m, 径向直径约占出口直径的70%, 且匀流区内的最大无量纲Mach数梯度仅为0.75%.

图 10为风洞运行过程中的密度梯度云图, 其中包含了膨胀波在储气段内传播的典型状态, 示色范围设为0～0.5， 以更好显示膨胀波的变化规律. 在t=22.3 ms时, 膨胀波刚好到达储气段弯曲处, 只有少部分靠近快开阀的气体跟随膨胀波开始流动. 之后膨胀波进一步向上游传播, 到t=29 ms时已完全通过U型管, 此时由于U型管的弯曲引起的流动不均匀性, 其内依旧留有较弱的密度梯度. 当膨胀波通过第2个U型管时, 可发现相同的密度梯度残留. 在t=61.1 ms之后不久, 膨胀波到达储气段末端并发生反射, 强度较刚开始传播时已明显减弱, 此时由于高压部分的气体流出, 储气段的流场整体呈现动态变化, 密度也因此变得不均匀.

同时监测风洞运行过程中储气段出口处压力的变化趋势(见图 11), 发现在Ludwieg管风洞运行期间储气段压力几乎维持恒定, 但是会随着风洞的运行有小幅下降, 在一个运行周期内其总压下降约为0.6%, 风洞的有效运行时间约为121 ms. 进一步放大恒压曲线可知, 在t=43 ms和83 ms时, 由于储气管的弯曲, 会引起小幅压力振荡, 但其最大无量纲压力梯度仅为0.04%, 该影响基本可忽略不计.

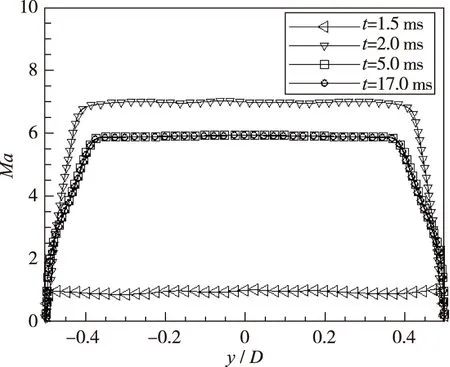
图7 Ludwieg管启动过程Mach数Fig. 7 Mach number for the starting process of Ludwieg tube

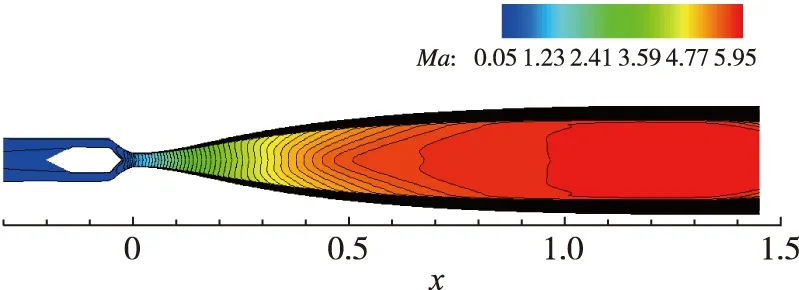
图8 喷管Mach数云图Fig. 8 Mach number contour of tunnel

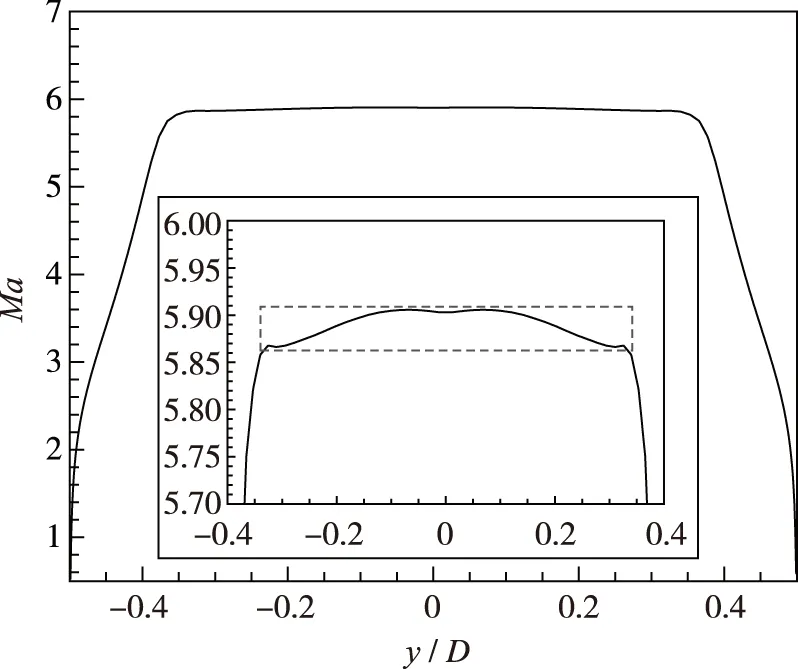
图9 喷管出口Mach数分布Fig. 9 Mach number slice across the test section

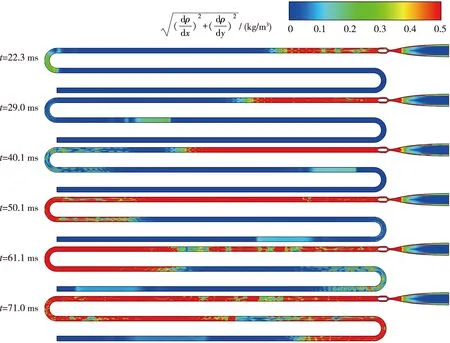
图10 Ludwieg管风洞运行过程密度梯度云图Fig. 10 Density gradient contour of HLT working process

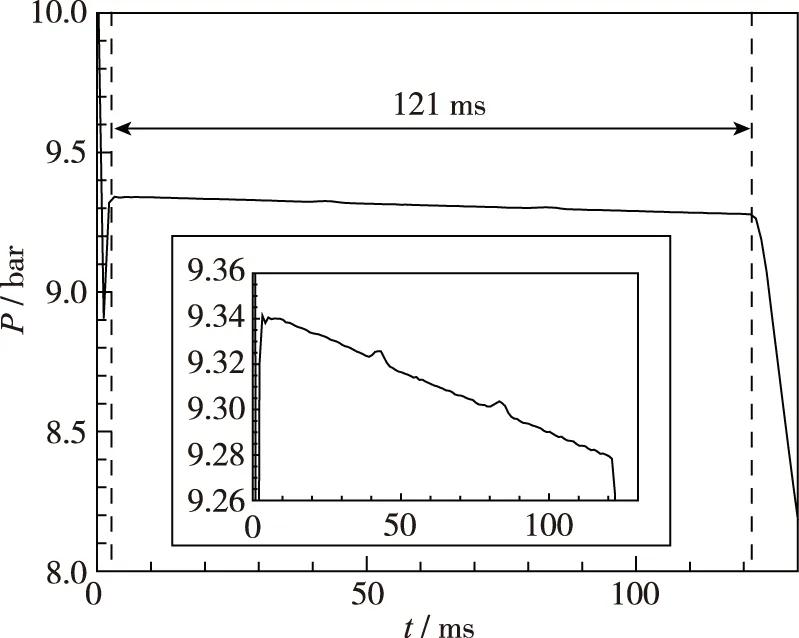
图11 风洞运行时储气段出口压力随时间变化曲线Fig. 11 Time trace of storage tube outlet pressure during running process

2 Ludwieg管风洞来流测量

华中科技大学Φ0.25 m Mach 6 Ludwieg管风洞于 2020 年完成搭建与调试, 如图 12所示. 该风洞由双弯储气段、 快开阀、 Laval喷管、 实验段、 扩散段以及真空罐组成, 占地面积约18 m2; 风洞突破主控快开阀技术, 可实现快开阀5 ms 内启闭; 运行间隔时间约为10 min, 每天可运行60车次以上.

2.1 测量方法

2.1.1 压力传感器

本文静态Pitot压力测量过程中采用的是Kulite传感器, 型号为XCQ-062系列快速动态压力传感器, 该传感器工作温度范围为-55～120℃, 传感器测量精度为0.02%(以传感器量程无量纲化的传感器底噪), 有效频率最高达240 kHz.

动态测量采用的是PCB132B38高频压电式传感器, 该传感器工作温度范围为-25～79℃, 压力测量分辨率为 7 Pa, 有效动态响应范围为 10～1 000 kHz.

所有传感器的输出信号由Spectrum A/D卡采集, 采集系统垂直分辨率16 bit, 采样频率3 MHz.

图12 华中科技大学Φ0.25 m Mach 6 Ludwieg管风洞Fig. 12 Mach 6 HUST-HLT

测压后的数据采用PSD功率谱密度进行分析. 1 s内的采样点共3×106个, 运用Welch方法, 选取Black-man窗函数. 窗大小为1 024点, 选取overlap为75%.

2.1.2 纹影系统

纹影系统采用灵敏度较高的锥形光纹影系统, 考虑到实验设备的尺寸以及实验场地的大小, 光路将采用反射式光路进行设计(见图 13). 纹影图像由IDT-NX系列高速相机拍摄, fps=1 000, 单幅图像的时间步长为1 ms.

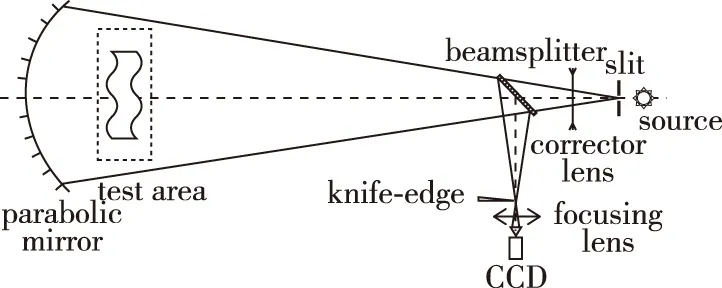
图13 纹影光路图Fig. 13 Schlieren optical path diagram

2.2 静态流场标定

首先, 通过在试验段的Pitot管上安装Kulite压力传感器测量来流总压以反映Ludwieg管风洞的有效运行时间. 图 14显示了来流总压为10 bar时试验段Pitot测量压力随时间的变化. 由图可知, 该Ludwieg管风洞的有效运行时间约为116 ms, 与CFD预测相吻合. 压力随时间的无量纲偏差小于0.1%, 表现出较高的流动质量, 因此在目前的设计中, 弯曲储气段的影响似乎可以忽略不计.

将Pitot管的纹影图像与相同流动条件下的CFD模拟结果进行了对比， 如图 15所示. 除数值模拟的激波由于数值耗散而在远离Pitot管头部时消失外, 所得弓形激波的形状与实验测得结果基本一致, 可认为该Ludwieg管试验段已实现了稳定的Mach 6高超声速来流.

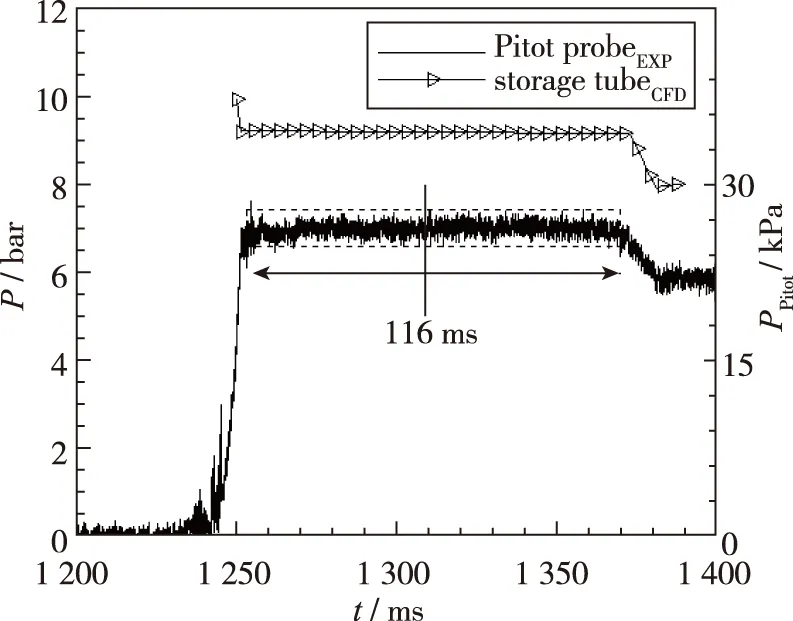
图14 储气段压力与试验段Pitot管压力随时间的变化Fig. 14 Time trace of storage tube and Pitot probe pressure in test section

图15 CFD与Pitot管探头激波结构实验比较Fig. 15 Shock structure comparison between CFD and experiments for Pitot probe

2.3 动态流场标定

沿Laval喷管壁面的高超声速湍流噪声辐射是高超声速风洞中主要扰动来源, 而只有少数研究进行了高超声速自由来流扰动的详细分析[22-23]. 如Laufer所述, 压力波动的测量有几种误差来源. 此外, 由于自由流扰动在穿过探针前的弓形激波时发生了转换, 从而导致了压力和熵波动的结合, 因此对驻点探针测量结果的解释变得复杂. 然而, 尽管存在困难, 直接从驻点探针获得的压力波动对于比较和表征不同设备的流动质量非常有价值.

通过从PCB传感器的信号中提取压力波动的RMS值可比较不同风洞之间的噪声水平. 图 16显示了布伦瑞克大学HLB风洞、 美国空军学院的HHK-6风洞和华中科技大学HUST风洞在同一位置Z=0 mm(风洞轴线处)的RMS数据比较. 这3座风洞中使用了相同的测量设备, 具有相同的传感器和信号调节器. 信号滤波范围5～100 kHz, 用压力波动除以传感器的平均滞止压力来归一化压力波动〈SPP〉=P′rms/P0.根据3座风洞中所得的数据, 波动强度均会随Re/l的增大呈下降趋势.

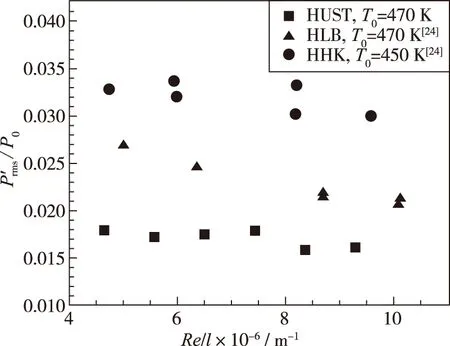
图16 HHK-6、 HLB和HUST风洞在5～100 kHz之间PCB传感器的归一化压力波动[24]Fig. 16 Normalized pressure fluctuations from PCB sensor from 5 kHz to 100 kHz in HHK-6, HLB and HUST

总体而言, HUST风洞的噪声低于HHK-6与HLB风洞里的噪声, 体现出该风洞的流场品质优秀.

图 17显示了PCB信号的功率谱密度曲线. 在Re/l= 5×106～10×106/m范围时, HUST的幅值均低于HHK-6与HLB的幅值, 进一步体现了本风洞来流扰动幅值较之其他两座Ludwieg管风洞要低, 适合开展高超声速边界层自然转捩基础研究.

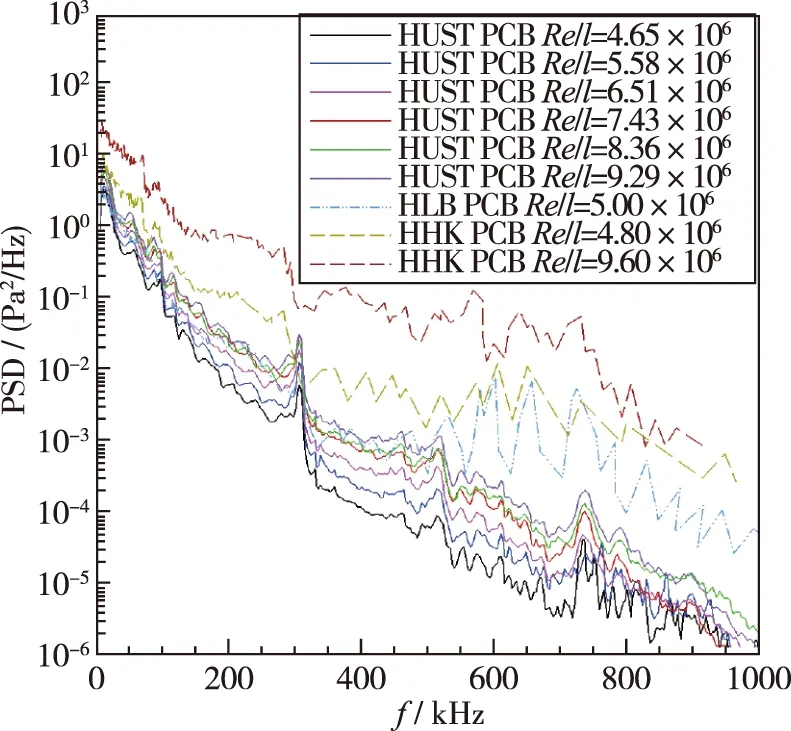
图17 从PCB得到的压力波动PSD[24]Fig. 17 PSD of pressure fluctuation obtained from PCB

3 7°半张角标准尖锥模型转捩实验

3.1 高超声速边界层转捩标准模型

高超声速边界层转捩实验模型为标准7°半张角尖锥模型, 模型前缘钝度为50 μm, 整体长度为0.4 m. 模型整体采用不锈钢材质加工而成, 分为4节, 不同节之间可以同轴旋转, 模型表面加工粗糙度Ra=3.2. 为了获取不稳定波沿着尖锥模型表面的增长特征, 将7枚高频PCB传感器采用齐平式安装方式布置在了尖锥模型上, 具体分布位置如图 18所示.

图18 尖锥模型及测点位置Fig. 18 Cone model and measuring point locations

3.2 高超声速边界层转捩实验

在保持风洞来流驻点温度不变的情况下, 通过调整风洞的驻点压力, 研究了不同来流单位Reynolds数条件下7°半张角尖锥模型表面的不稳定波特征. 当来流单位Reynolds数为Re/l=4.65×106/m时, 7枚PCB压力传感器均测得了不稳定波, 可知尖锥表面为层流边界层. 在x=182.6 mm处, 不稳定波的频率带宽为175～220 kHz, 但是幅值较低; 随着不稳定波沿流向发展, 边界层逐渐增厚, 不稳定波的频率呈降低趋势, 但是不稳定波的幅值持续增长. 根据第二模态不稳定波波长与边界层厚度的关系, 可以基本确定该不稳定波为第二模态不稳定波, 即Mack 波. 当自由来流Reynolds数增加到Re/l=5.58×106/m时, 第二模态不稳定波在x=182.6 mm处已经较为明显, 随着流动的发展, 不稳定波的幅值进一步增长, 但是当流动发展到尖锥模型尾端时(x=357 mm), 第二模态不稳定波的频谱特征逐渐消失, 但是其低频和高频部分(第二模态不稳定波频率以外区域)的幅值较高, 意味着边界层此时处于转捩过程, 如图 19(b)所示. 当来流Reynolds数进一步增大到Re/l=6.51×106/m时, 转捩位置由之前的x=357 mm前移到了x=337 mm. 随着来流Reynolds数的进一步增加, 尖锥模型表面转捩位置逐渐前移, 当来流Reynolds数到达Re/l=9.29×106/m时, 边界层转捩的位置前移到了x=207.4～232.2 mm之间, 如图 19(f)所示.

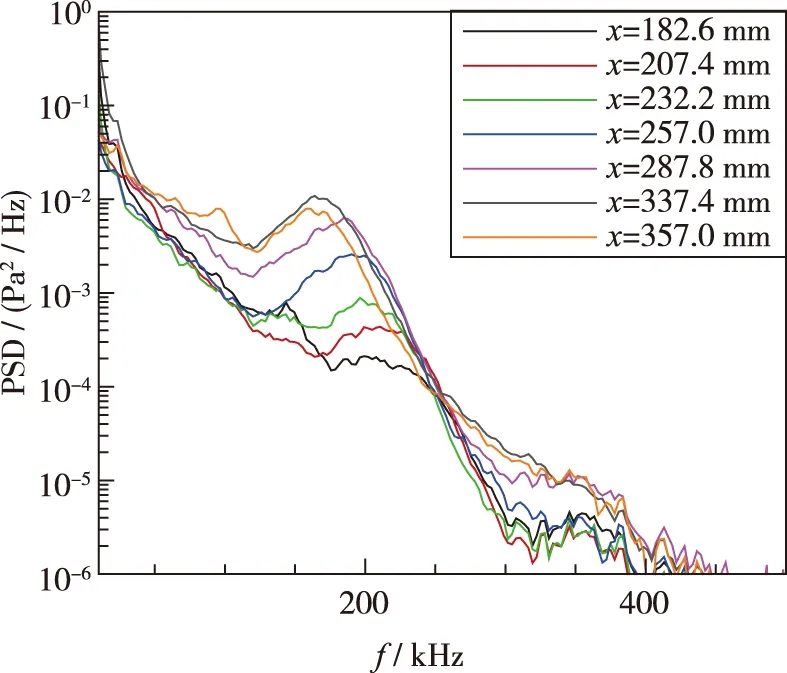
(a) Re/l=4.65×106/m

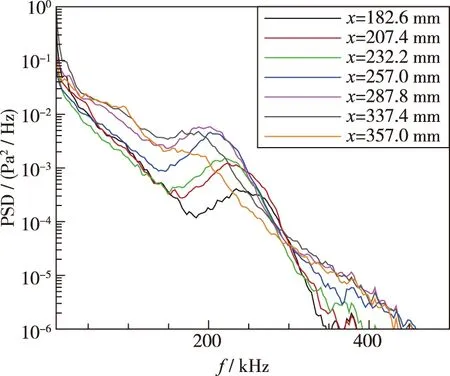
(b) Re/l=5.58×106/m

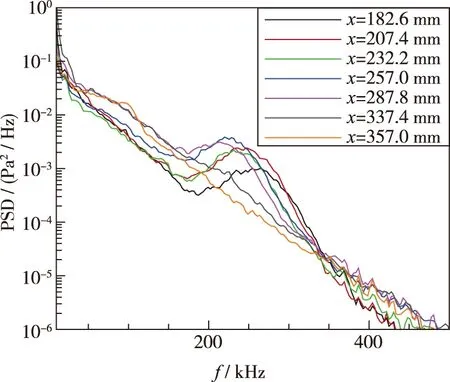
(c) Re/l=6.51×106/m

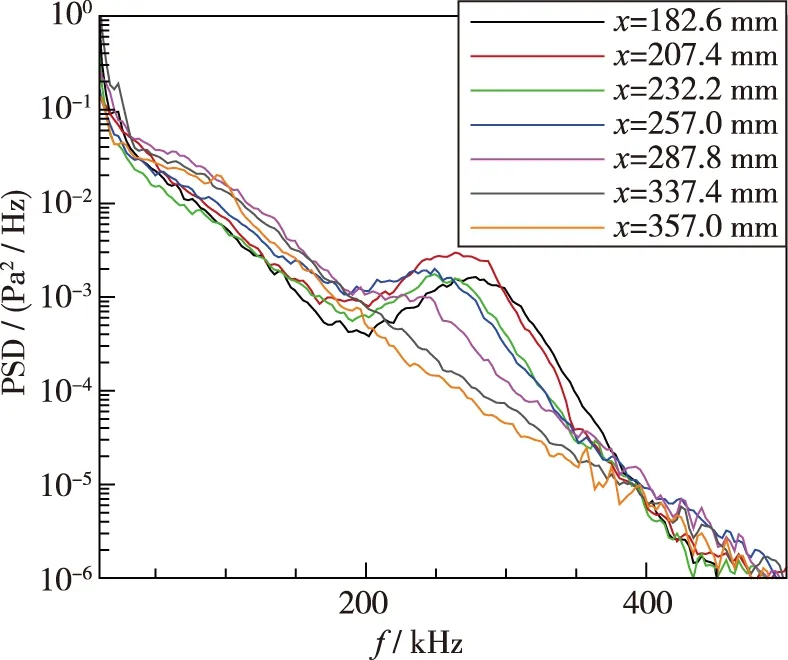
(d) Re/l=7.43×106/m

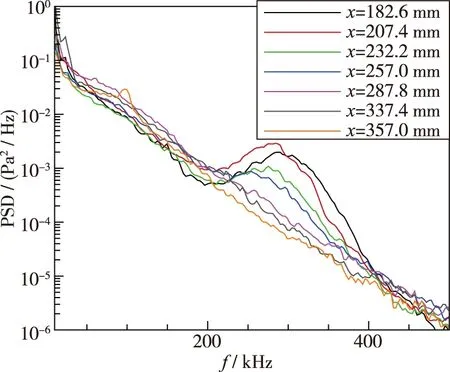
(e) Re/l=8.36×106/m

(f) Re/l=9.29×106/m

基于图 19(a)的频谱分析结果, 通过对Re/l=4.65×106/m时不同测点位置的原始压力信号进行120～250 kHz的带宽滤波, 得到结果如图 20(a)所示(最下端曲线对应的测点位于尖锥最前端), 发现前6个测前位置处均有较明显的第二模态波包, 波包随时间向下游传播, 且幅值逐渐变大.

基于图 19(f)的频谱分析结果, 通过对Re/l=9.29×106/m 时不同测点位置的原始压力信号进行230～400 kHz的带宽滤波, 得到结果如图 20(b)所示, 尖锥前缘的波包幅值沿来流方向逐渐减小并消失不见, 流动从3号测点位置开始转捩, 最终在6, 7号测点流动完全变为湍流.

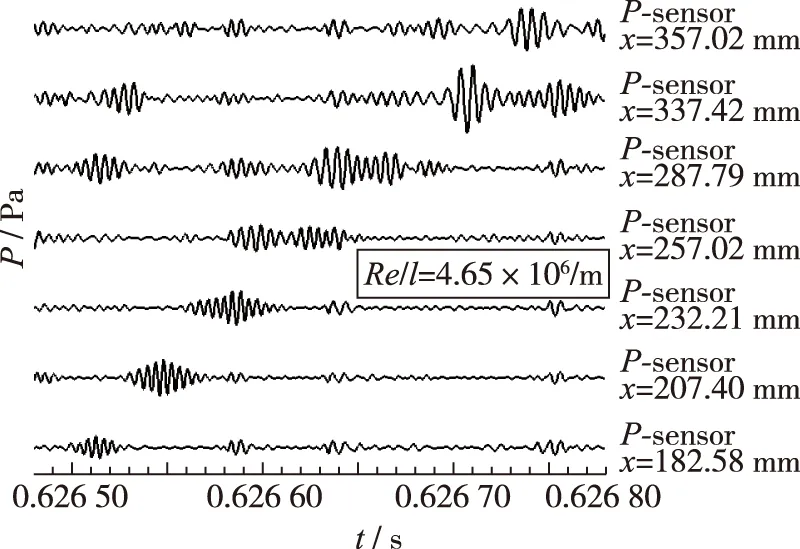
(a) Re/l=4.65×106/m

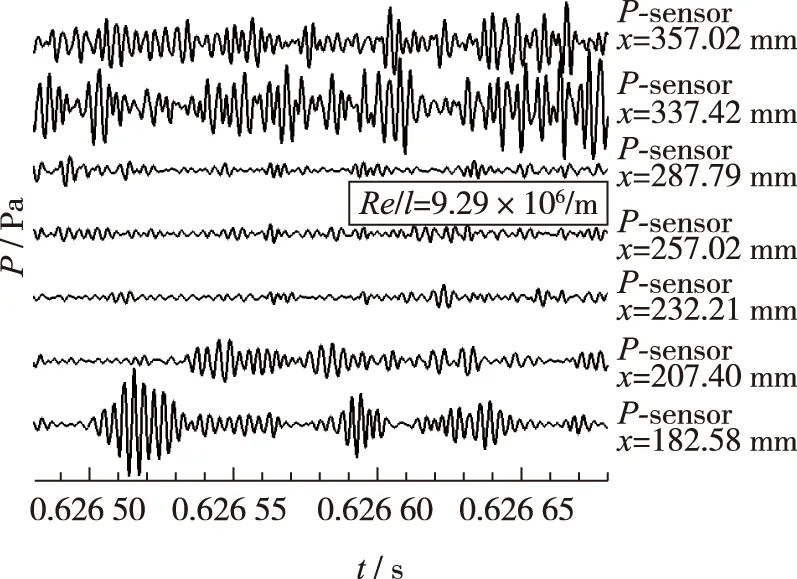
(b) Re/l=9.29×106/m

为获取第二模态波的相速度, 对不同测点的压力信号xn,yn(长度为N)进行互相关分析

图 21所示为Re/l=7.43×106/m情况下3, 4号压力信号的互相关曲线(测点相距25 mm), 此时两个测点之间的时间偏移量为32.333 μm, 计算得相速度约为773.2 m/s(87%的边界层外缘速度Ue), 与Stetson等曾提出的结论相一致[25].

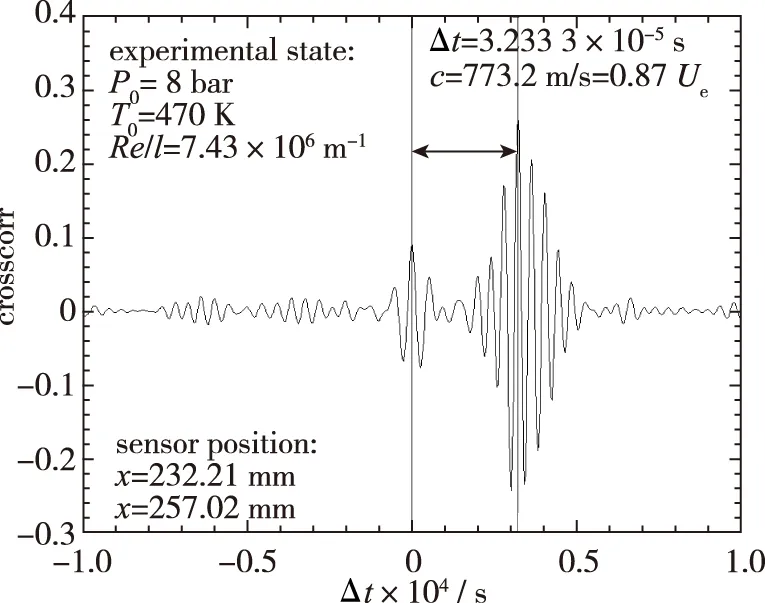
图21 压力信号互相关曲线Fig. 21 Cross-correlation of pressure signals

4 结论

华中科技大学Mach 6 Ludwieg管风洞的建成， 突破了毫秒级快开阀技术难题; 该风洞运行效率高、 成本低且操作简单; 可模拟单位Reynolds数范围5×106～3×107/m, 有效运行时间达100 ms以上; 风洞来流品质较好, 适合进行高超声速边界层转捩等基础研究.

(1)基于MOC方法设计优化了喷管型线, 并通过对试验段的平均流场参数分布, 确定了生成型线的质量, 获得流动均匀的试验菱形区, Mach数在试验段的相对偏差小于0.75%.

(2)对全风洞进行了非定常数值模拟, 重点研究了沿Laval喷管流动的启动过程与运行状态. 结果表明, 使用快开阀的喷管可在5 ms内建立起稳定的高超声速流动; 风洞运行期间膨胀波的强度随其传播过程而逐渐降低, 尽管弯曲储气段设计会引起压力振荡(小于0.04%), 但其对膨胀波的影响几乎可以忽略不计, Laval喷管的高超声速流动状态在运行过程中保持恒定.

(3)采用纹影和Pitot探头对流场品质进行了实验校测. 结果表明, 本风洞在冷温运行下的有效运行时间约为116 ms, 压力随时间的无量纲偏差仅不到0.1%; 在热温运行下的扰动幅值与HHK-6和HLB相比下降20%～50%, 显示了优秀的动态流场品质.

(4)进行了标准尖锥模型转捩实验, 获取了不稳定波沿尖锥模型表面的增长特征, 所测量的第二模态波相速度为773.2 m/s, 约为87%的边界层外缘速度, 与早期的测量结果相近.

综上所述, 本文阐述了高超声速Ludwieg管风洞的气动设计, 评估了风洞的流场品质, 验证了其进行高超声速边界层转捩实验的能力. Ludwieg管的建成对拟开展高超声速风洞基础实验研究的科研机构提供了经验. 后期, 本团队将进一步在高超声速Ludwieg管风洞自由来流扰动特性、 高超声速转捩预测与控制等方面开展相关研究.