高超声速飞行器复杂外形转捩预测

李 齐, 董 颖, 赵雅甜, 赵 瑞

(1. 北京空间飞行器总体设计部, 北京 100094; 2. 北京理工大学, 北京 100081; 3. 中南大学, 湖南长沙 410083)

引 言

在高超声速飞行器的飞行高度、 速度和Reyno-lds数范围内非常容易出现边界层转捩[1-2], 转捩后壁面摩阻和热流可增大数倍之多, 严重影响飞行器的气动性能和热防护系统[3-4], 造成壁面烧蚀严重、 颤振加剧、 姿态控制困难等后果[2]. 因此, 研究高超声速边界层转捩问题, 准确预测边界层的转捩起始位置, 对飞行器的气动设计和热防护设计至关重要.

近几十年来人们对边界层转捩预测开展了全面的探索和研究[5]. 当前, 面向高超声速复杂外形飞行器的边界层转捩预测手段, 主要包括实验研究、 基于稳定性理论的eN方法、 转捩准则以及模式理论. 实验研究具有直观性、 真实性的特点, 面向边界层转捩的实验研究主要包括飞行试验和风洞试验两大类. 其中具有代表性的飞行试验工作如: 美国的HyBoLT(Hypersonic Boundary Layer Transition)计划[6]、 法国的LEA项目[7]、 欧洲的EXPERT(European Experimental Reentry Testbed)项目[8]等. 2015年12月完成的MF-1飞行是我国高超声速模型飞行试验历史上首次以空气动力学基础研究为目的的飞行试验[9]. 飞行试验花费极其高昂, 试验的设计周期也较长. 为了复现高空飞行条件下边界层转捩过程, 实现转捩预测结果的天地一致性, 静音风洞应运而生. Yao等[10]在Ma=6静音风洞中对平板三角翼的边界层转捩情况进行了研究, 分析了攻角和Reynolds数对边界层转捩的影响, 结果表明, 侧线边界层的转捩比中线边界层的转捩早, 大攻角促进边界层的转捩. 随着Reynolds数增加, 边界层的转捩位置向上游移动. Lu等[11]在Ma=6高超声速低噪声风洞中对45°后掠平板边界层转捩过程进行了研究, 得到了边界层从层流到湍流的时空演变特征. 刘向宏等[12]总结了有关高超声速边界层转捩实验研究.

eN方法基于稳定性理论得到主要扰动的增长率, 通过经验参数N判断转捩, 其估算转捩位置和范围的技术水平取决于对所涉及的物理机理的了解程度[13]. 转捩准则是根据大量地面实验和飞行试验数据拟合得到的有效经验公式[14]. 历史上, 针对各类湍流问题突出的飞行器均发展了相应的转捩判据, 如Potter & Whitfield转捩判据(1962), Van Driest-Blumer转捩判据(1967), PANT转捩判据(1975), Boudreau转捩判据(1981),Reθ/Me判据(1997), BLT判据[14]等. 孔维萱等[15]提出“层流+转捩准则模型”来预测流向不稳定失稳诱导形成的边界层自然转捩, 周玲等[16]在此基础上增加了横流转捩准则判据.

转捩模式是计算复杂外形转捩的主要方法, 包括基于当地变量的γ-Reθt模式[17-18], 适用于高超声速边界层转捩预测的k-ω-γ转捩模式[19-20]等.γ-Reθt模式已在低速边界层转捩流动模拟中获得了成功应用, 近年来有学者开始将其拓展至高超声速边界层转捩模拟[3]. Krause等[21]考虑来流湍流度构造了Flength和Reθc关系式, 较好地模拟了Ma=8.3的双楔壁面压力分布. Zhao等[22-23]评估对比了3种经典转捩模式(γ-Reθ,k-ω-γ和kT-kL-ω转捩模式)在高超声速复杂外形转捩预测中的性能表现. Zhou等[24-26]对k-ω-γ转捩模式进行了改进. 由于改进的k-ω-γ转捩模式采用网格预处理技术, 可以快速大规模并行获取具有非当地变量属性的边界层参数. 同时, 改进的k-ω-γ转捩模式考虑了横流转捩, 因此具有推广至工程复杂外形应用的潜力[27]. 曾宏刚等[28]针对高超声速飞行器前体及压缩面组合外形, 在Ma=6下采用k-ω-γ转捩模式预测转捩起始位置, 结果与风洞实验较为吻合. Zhao等进一步对k-ω-γ转捩模式经验参数[29]和来流扰动[30]导致的预测不确定性开展了不确定的量化分析工作. 本文转捩模式预测中即采用k-ω-γ转捩模式.

目前, 采用转捩模式预测工程复杂外形, 尤其是高超声速流动中复杂外形的转捩研究较少. 本文基于改进的k-ω-γ转捩模式对高超声速飞行器复杂主体外形进行了流场分析和转捩预测, 分析了Reynolds数和攻角对边界层转捩的影响, 为类似的工程应用提供参考.

1 数值方法

1.1 计算模型

该飞行器采用上反翼布局, 进气方式为背部进气, 飞行器总长45 m, 外形布局关键几何参数详见文献［31-32］. 由于计算工况无侧滑角, 因此采用半模计算. 计算网格为多区对接结构网格. 飞行器半模总网格量6.7×106, 如图 1所示. 壁面第1层网格高度为0.001 mm, 保证y+≤1.

(a) Global grid topology

(b) Symmetry plane grids

(c) Wall grids图1 飞行器全机计算网格示意图Fig. 1 Computational zone and grid distribution of the configuration

1.2 转捩模式

本研究使用的k-ω-γ转捩模式以SST湍流模式为基础, 同时引入γ输运方程, 并进行了Reynolds数和横流转捩的预测修正. 该k-ω-γ模式的总体框架为

式中,Pγ和Dγ分别为γ输运方程的生成项和耗散项, 基于量纲分析构造, 具体表达式为

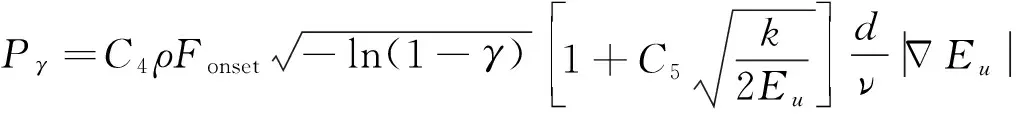
本文选取有限体积方法求解控制方程. 层流N-S方程和湍流、 转捩输运方程采用统一的离散方式: 无黏通量采用差分分裂的Roe格式, 网格界面上采用MUSCL(monotone upstream-centered schemes for conservation laws)格式插值获得高阶精度; 黏性项采用2阶中心差分格式进行离散; 时间推进采用隐式LU-SGS(lower-upper symmetric Gauss-Seidel)格式. Zhou等[26]将改进的k-ω-γ模式用于预测X-51A飞行器前体的边界层转捩, 得到了和风洞实验一致的结果. 同时与Reθ/Me转捩准则的预测结果进行了对比, 结果较为吻合, 因此本文不再赘述算法验证, 计算方法相关验证细节可参考文献[26].

计算的来流条件为: 飞行高度分别为H=25， 35 km, 飞行Mach数为Ma=6, 攻角分别为α=0°， 5°, 壁面温度为Tw=300 K, 不同飞行高度对应的单位Reynolds数分别为Re=4.9×106， 1.0×106/m, 以研究不同Reynolds数和攻角对飞行器边界层转捩的影响.

2 流场分析

图2 对称面和流向截面等Mach线分布(4个截面位置分别为x/L=0.1,0.3,0.6,0.9, L为机身全长)Fig. 2 Mach number distribution on the symmetry plane and flow cross sections(The four sections are at x/L=0.1,0.3,0.6, 0.9, respectively, L is the total length of aircraft body)

图3 流向截面无量纲压力云图(4个截面位置分别为x/L=0.1,0.3,0.6,0.9) Fig. 3 Normalized pressure contours at four sections: x/L=0.1, 0.3, 0.6, 0.9

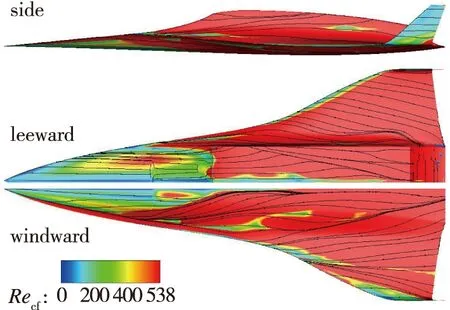
图4 横流Reynolds数Recf和表面极限流线分布Fig. 4 Recf and limit streamline distribution on the vehicle surface

3 转捩预测结果分析

采用转捩模式对飞行器在不同Reynolds数(高度)、 攻角条件下的边界层转捩位置进行预测. 本文采用的转捩模式考虑了第一模态、 第二 Mack模态以及横流模态, 用于预测流向不稳定和横流不稳定诱导的转捩. 通过飞行器壁面间歇因子的变化判断飞行器全机边界层自然转捩起始位置的分布. 重点分析了飞行器背风面、 迎风面和侧面转捩区域的分布; 同时对头部和舵面两处局部结构的转捩起始位置进行了详细分析.

3.1 Reynolds数对转捩的影响

图 5为0° 攻角时不同Reynolds数条件下飞行器全机壁面间歇因子分布云图. 转捩模式计算将间歇因子γ=0.2～1的范围定义为转捩区. 整体而言, 随着飞行高度的增加, 来流密度减小, 自由来流Reynolds数逐渐降低, 转捩位置明显滞后. 注意到, 图 6中背风面中心线附近转捩位置较展向其他位置提前, 呈现明显的“凸”字型转捩阵型, 对比图 4表面极限流线分布可以看到, 相应位置处发生了流动分离, 因此“凸”字型转捩阵型是由于进气道压缩面逆压梯度诱导产生小的流动分离, 流动分离诱导了提前转捩. 进气道喷管区域由于膨胀加速效应, 在顺压梯度的作用下使得流动再层流化. 机翼前缘横流效应并不显著(见图 4), 该处转捩主要由流向不稳定模态主导(见图 7).

(a) Re=4.9×106/m

(b) Re=1.0×106/m图5 不同Reynolds数下壁面间歇因子分布云图 (α=0°)Fig. 5 γ distribution on the vehicle wall at different Reynolds numbers(α=0°)

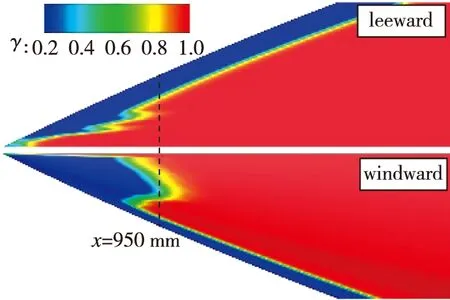
(a) Re=4.9×106/m

(b) Re=1.0×106/m图6 不同Reynolds数下头部壁面间歇因子分布云图(α=0°)Fig. 6 γ distribution on the vehicle head wall at different Reynolds numbers(α=0°)

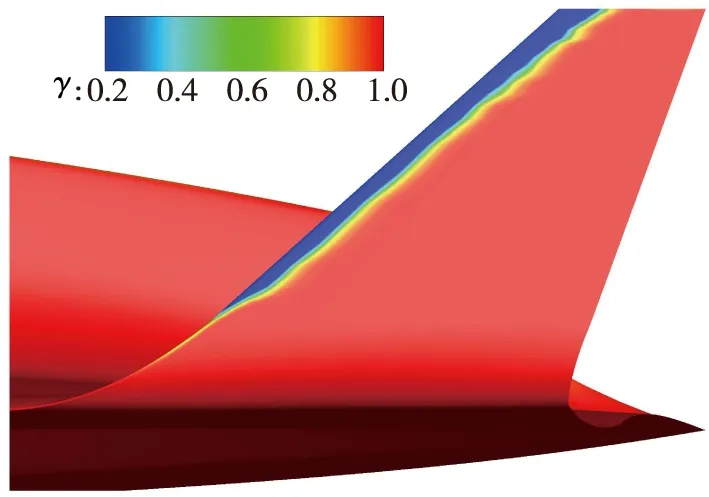
图7 不同Reynolds数下舵面间歇因子分布云图(α=0°)Fig. 7 γ distribution on the rudder wall at different Reynolds numbers(α=0°)

横流Reynolds数Recf常用来判断流场中横流区域分布及其强度.Recf的表达式为Recf=δ0.1wmax/ve, 其中δ0.1是当地横流速度满足w/wmax=0.1的壁面法向距离,wmax为边界层内最大横流速度,ve为边界层外缘分子运动黏性系数. 横流Reynolds数越大, 说明横流效应越强. 一般认为, 对于可压缩流动,Recf大于其临界值200～400即可认为横流诱导转捩发生. 结合图 4可知, 迎风面和背风面大面积的转捩均由横流不稳定主导.

3.2 攻角对转捩的影响

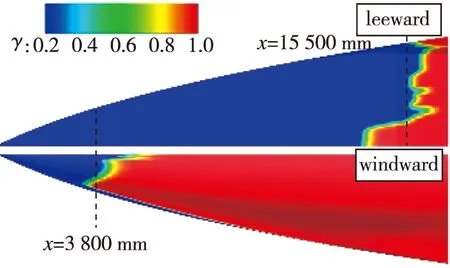
图 8为5° 攻角,Re=1.0×106/m下飞行器全机壁面间歇因子分布云图. 与图 5(b)对比可知, 随着攻角增大, 头部以及机翼转捩位置向上游移动, 背风面喷管区域层流面积增加. 图 9为5° 攻角下头部和舵面的局部细节图, 经定量比较可以看出攻角增加导致头部迎风面和背风面转捩起始位置均前移. 舵面转捩受攻角影响不大, 这是因为舵面边界层转捩由流向不稳定主导, 对于本文外形, 攻角对流向不稳定影响较小. 图10给出了不同攻角下的对称面无量纲压力云图, 随着攻角增加, 迎风面前缘斜激波更强, 背风面进气道压缩激波减弱, 喷管区域膨胀效应增强. 飞行器迎风面压力增大, 背风面压力减小, 头部附近背风面与侧边的展向压力梯度增大, 横流效应增强. 如图 11所示, 背风面流动汇聚线向上游移动, 汇聚线下游的横向流动更加显著, 导致转捩提前. 0°攻角下由流动分离诱导产生的“凸”字型转捩型线不再存在, 对比图 11可知, 5°攻角下流动分离发生在转捩之后, 故“凸”字型消失. 迎风面的转捩起始位置前移则是由攻角的增大导致头部激波增强, 波后密度增加, 如图 12所示, 边界层外缘Reynolds数增大, 导致转捩提前.

图8 壁面间歇因子分布云图(α=5°, Re=1.0×106/m)Fig. 8 γ distribution on the vehicle wall(α=5°, Re=1.0×106/m)

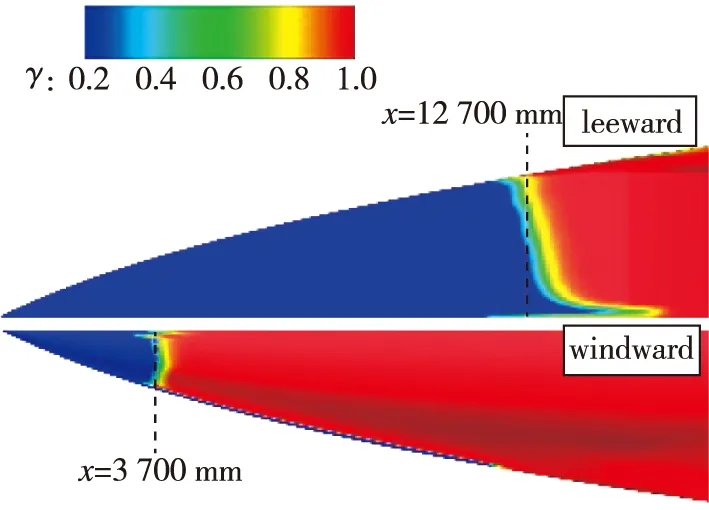
(a) Head

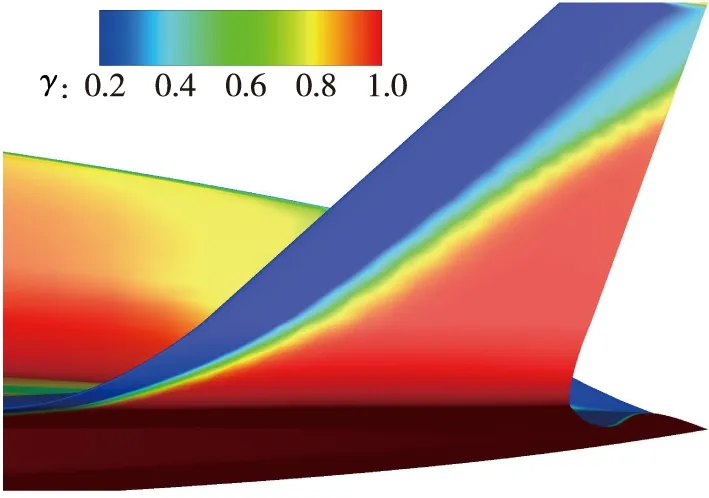
(b) Rudder图9 局部壁面间歇因子的分布云图(α=5°, Re=1.0×106/m)Fig. 9 γ distribution on the local wall(α=5°, Re=1.0×106/m)

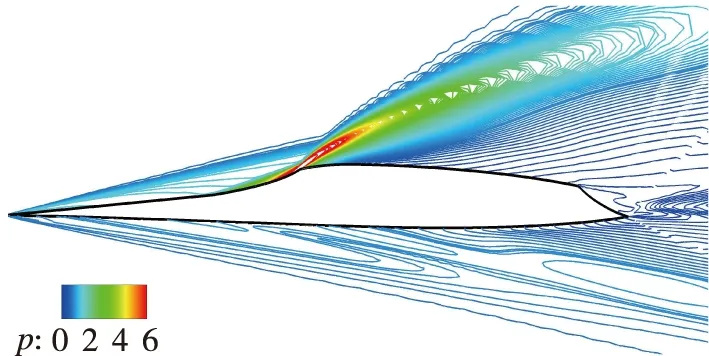
(a) α=0°

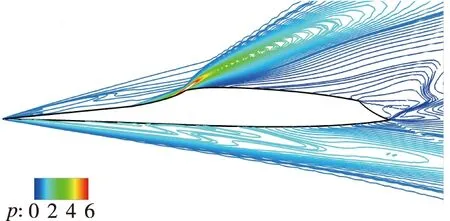
(b) α=5°图10 不同攻角下对称面无量纲压力云图(Re=1.0×106/m)Fig. 10 Pressure distribution on symmetry plane at different angles of attack(Re=1.0×106/m)

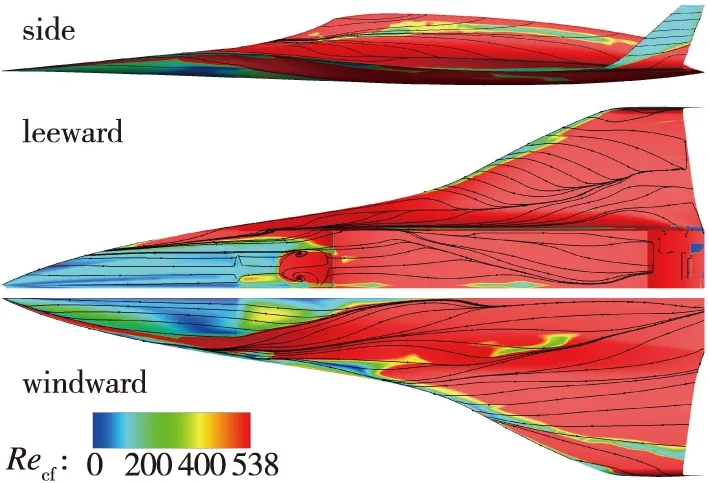
图11 横流Reynolds数Recf和表面极限流线(Re=1.0×106/m, α=5°)Fig. 11 Recf and limit streamline distribution on the vehicle wall(Re=1.0×106/m, α=5°)

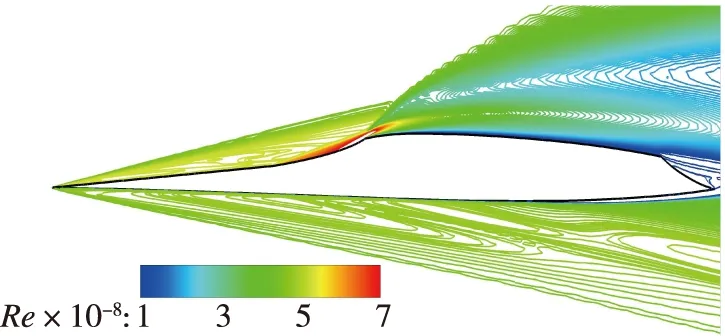
(a) α=0°

(b) α=5°图12 不同攻角下对称面Reynolds数云图(Re=1.0×106/m)Fig. 12 Reynolds number distribution on symmetry plane at different angles of attack(Re=1.0×106/m)

4 结论

本文以高超声速飞行器复杂外形为研究对象, 采用改进的k-ω-γ转捩模式对主体外形进行了流场分析和边界层转捩预测, 并分析了Reynolds数和攻角对边界层转捩的影响. 研究得到的主要结论如下:

横流是影响飞行器大面积转捩的主要因素. 复杂飞行器外形由于侧缘和机翼尖前缘激波后压力较大, 形成展向压力梯度, 使得迎风面和背风面大部分区域转捩主要由横流主导. 随着高度增加, 来流Reynolds数减小, 迎风面和背风面的转捩起始位置均向下游移动. 攻角增大导致头部激波增强, 波后迎风面密度增加, 边界层外缘Reynolds数增大, 导致转捩提前. 背风面尾喷管区域存在膨胀加速效应, 在顺压梯度的作用下存在再层流化, 攻角增大后膨胀效应增强, 层流区域增加. 0°攻角下由于背风侧进气道压缩面逆压梯度诱导产生小的流动分离, 流动分离诱导了提前转捩, 形成“凸”字型转捩型线; 5°攻角下背风面横流效应增强, 流动分离发生在转捩之后, “凸”字型不再存在.