偏翼标模小滚转力矩测量与气浮轴承动态特性研究

梁 彬, 付增良, 岳才谦, 赵俊波

(中国航天空气动力技术研究院, 北京 100074)

引 言

针对再入飞行器再入过程中由于气动烧蚀作用产生小不对称滚转气动力带来的诸多问题[1-3], 需要在实验中对该小滚转气动力进行准确测量. 基于气浮轴承的自由滚转实验技术是测量再入飞行器小不对称滚转气动力的重要方法, 该方法相对于固定式天平实验技术[4-6], 测量精度较高, 且不仅能够对小量级的滚转力矩系数进行准确测量, 还能同时获得滚转阻尼导数[7-10].

气浮轴承自由滚转实验技术在约20年前开始应用于风洞实验研究[7], 在近年来得到了成熟发展和应用, 进一步获取了滚转力矩的周期性动态波动量[8], 并针对大口径风洞进行了实验系统的优化改进和创新, 进一步提高了实验Mach数和实验攻角[9].

针对气浮轴承自身动态特性, 以及自由滚转这种特殊的实验方法应用, 对实验结果有怎样的影响、 对实验系统的误差分析在以往的研究工作中较少. 如文献[7-8]中仅对气浮轴承进行了无风实验标定, 对比实验结果说明了量级差别, 缺少详细的误差分析结果. 本文针对气浮轴承自由滚转实验系统的特点, 对气浮轴承进行了无风实验标定和真空实验标定以及动态特性分析, 进一步对各误差来源分别进行分析讨论, 并给出了综合误差分析结果、 定量表示了实验系统对实验测量结果的影响. 研究结果对气浮轴承自由滚转实验精度提高、 方案设计和设备研制等具有重要的实际意义.

1 方法和原理

1.1 实验原理

气浮轴承自由滚转实验系统的基本原理和方法在文献[7-10]中均有详细描述, 这里简要介绍.

风洞启动后模型在风洞中作自由滚转运动, 滚转运动方程为

(1)

其中,P为滚转转速;I为滚转转动惯量;D为参考长度, 取模型底部直径;V为来流速度;q为来流动压;s为参考面积, 取模型底部面积;Cl0和Clp分别为研究对象待测量滚转力矩系数和滚转阻尼导数, 实验后通过参数辨识获取.

根据实验经验, 相似尺寸的气浮轴承在相似工况下性能差异不大, 本文研究时采用了标号QF104的气浮轴承, 尺寸约Φ104 mm×172 mm, 如图1所示.

图1 气浮轴承QF104Fig. 1 Photo of air bearing QF104

实验实际过程中, 由于气浮轴承内部空气的滚转摩擦阻尼作用, 以及气浮轴承加工偏差和内部气流的作用下, 产生固有不对称附加滚转力矩, 模型自由滚转运动控制方程(1)可改写为

(2)

其中,δL0,a和δLp,a分别为气浮轴承附加滚转力矩和附加滚转阻尼力矩. 上述两个参数是描述气浮轴承性能和动态特性的重要参数.

本文研究中如无特殊说明, 进行无风实验、 风洞实验和误差分析时所使用和参考的数据处理方法, 均采用了气浮轴承自由滚转实验中最基础和常用的实验数据处理方法[7].

1.2 误差分析方法

影响气浮轴承自由滚转实验系统测量结果的因素主要包括: 气浮轴承动态特性、 原始数据采集测量误差、 参数辨识误差、 模型加工和安装误差、 风洞气流参数误差等. 其中模型加工和安装误差与实验研究对象有关、 风洞气流参数误差与实验风洞有关. 本文仅针对实验系统自身特性造成的测量误差进行分析讨论.

首先， 考虑气浮轴承动态特性对测量结果的影响. 由于气浮轴承附加滚转力矩δL0,a和附加滚转阻尼力矩δLp,a量级很小, 以往研究中气浮轴承自身动态特性对实验结果的影响一般采取忽略处理[7-10], 即控制方程简化为方程(1)所述. 但对于测量对象量级较小时, 仍需要考虑其对实验结果的影响, 其具体量值可通过气浮轴承的无风实验标定进行测量. 误差分析中该量可作为该气浮轴承风洞实验时的测量偏差, 或直接予以扣除. 无风实验标定时, 控制方程(2)可简化为

(3)

方程(3)与控制方程(1), (2)一样具有2阶微分方程的相同形式, 无风实验时原理和数据处理方法与有风实验时相同. 其中,δLp,a描述了气浮轴承内部空气的滚转摩擦阻尼作用,δLp,aP即气浮轴承内部空气的滚转摩擦阻尼力矩, 角速度越高, 摩擦阻尼力矩越大;δL0,a是由于气浮轴承的微小加工偏差, 内部气流产生的固有滚转力矩作用, 与气浮轴承加工精度有关. 两者均是物理存在的滚转力矩量, 无量纲后可分别写为:δCl0,a=δLp,a/(qsD),δClp,a=δLp,aV/(qsD2).

接下来分析原始数据采集和测量误差, 包括直接误差和间接误差. 根据气浮轴承自由滚转实验系统的传统测量方式[7-9], 直接误差包括时间测量误差和角位移测量误差, 是数据直接采集过程中产生的、 与测量设备性能直接相关的误差. 间接误差包括角速度误差、 角加速度误差、 转动惯量测量误差等根据原始数据处理得到的间接量的误差, 与测量和数据处理方法有关. 直接误差可根据测量设备性能指标直接给出, 本文分析间接误差.

首先, 分析角速度误差. 角速度一般采用2阶中心差分格式进行计算, 具有较高的精度和计算效率, 可描述为

Pi=(θi+1-θi-1)/(ti+1-ti-1)+O2

(4)

其中,P为模型角速度,θ为角位移,t为时间,O2为2阶截断误差. 可见角速度的测量误差来源于时间误差和角位移误差, 由于截断误差O2为高阶小量可忽略, 角速度误差可表示为

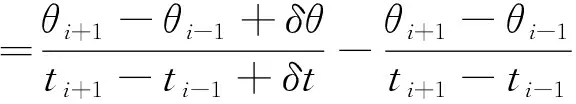
(5)

其中,δθ和δt分别为角位移和时间误差. 同理角加速度误差可表示为

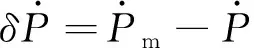
(6)

然后， 分析模型转动惯量. 模型转动惯量一般采用附加质量法[7-11]进行测量, 该方法测量精度和误差分析已有较成熟研究[12]. 根据文献[12]结果, 转动惯量测量相对误差δI/I约0.2%.

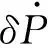
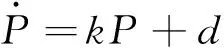
确定其中的斜率k=ClpqsD2/(VI)和截距d=Cl0qsD/I, 进而得到Cl0和Clp.根据最小二乘法原理[13], 可得其线性相关系数R, 标准偏差S, 系数偏差Sk和Sd分别为

(7)

(8)

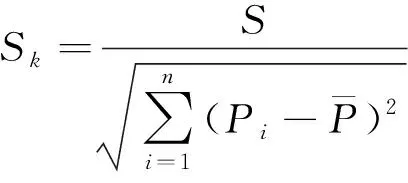
(9)

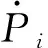
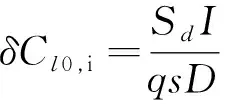
其中,δCl0,i的影响参数是实验原始数据点最小二乘法辨识的截距系数偏差Sd,δClp,i的影响参数是斜率系数偏差Sk.

2 结果

2.1 气浮轴承动态特性和标定结果

如前文所述, 气浮轴承动态特性可通过气浮轴承的无风实验标定进行评估.

首先, 分析附加滚转力矩δL0,a.表1给出了气浮轴承QF104无风实验条件下附加滚转力矩δL0,a的标定结果, 实验时供压为0.7 MPa.

从表1中结果可见, 气浮轴承的附加滚转力矩在低转速范围内较低、 在高转速范围内较高, 最大不超过0.2 mN·m. 根据控制方程(1), 阻尼项ClpqsD(D/V)P相对较小时可减小阻尼力矩对静力矩辨识的影响, 实际实验研究中常采用较低转速段的辨识结果作为滚转力矩系数置信度较高的结果, 同理低转速范围内的δL0,a标定结果置信度较高, 其平均量可作为该气浮轴承风洞实验时滚转力矩的测量偏差, 或直接予以扣除以减小这一偏差.

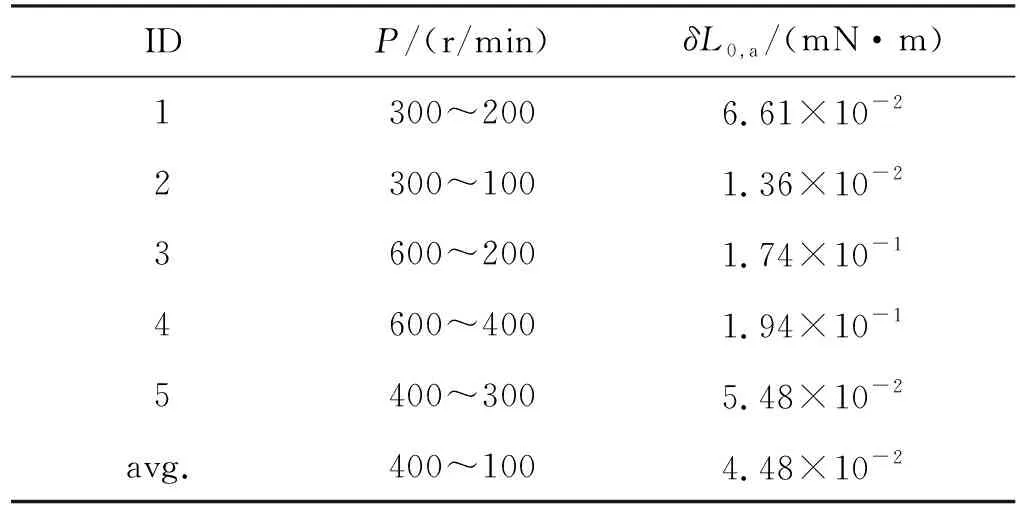
表1 附加滚转力矩无风实验标定结果

然后, 分析附加滚转阻尼力矩δLp,a.风洞实验时, 实验系统的滚转阻尼主要包括了气浮轴承内部空气对转子的摩擦阻尼和外部空气对模型外形的摩擦阻尼, 实验时需要测量后者并且考虑前者带来的误差. 仅进行无风实验无法排除外部空气阻尼对气浮轴承内部空气摩擦阻尼带来的误差. 表2分别给出了同一气浮轴承无风和真空实验条件(约 1 000 Pa)下附加滚转阻尼力矩δLp,a的标定结果.

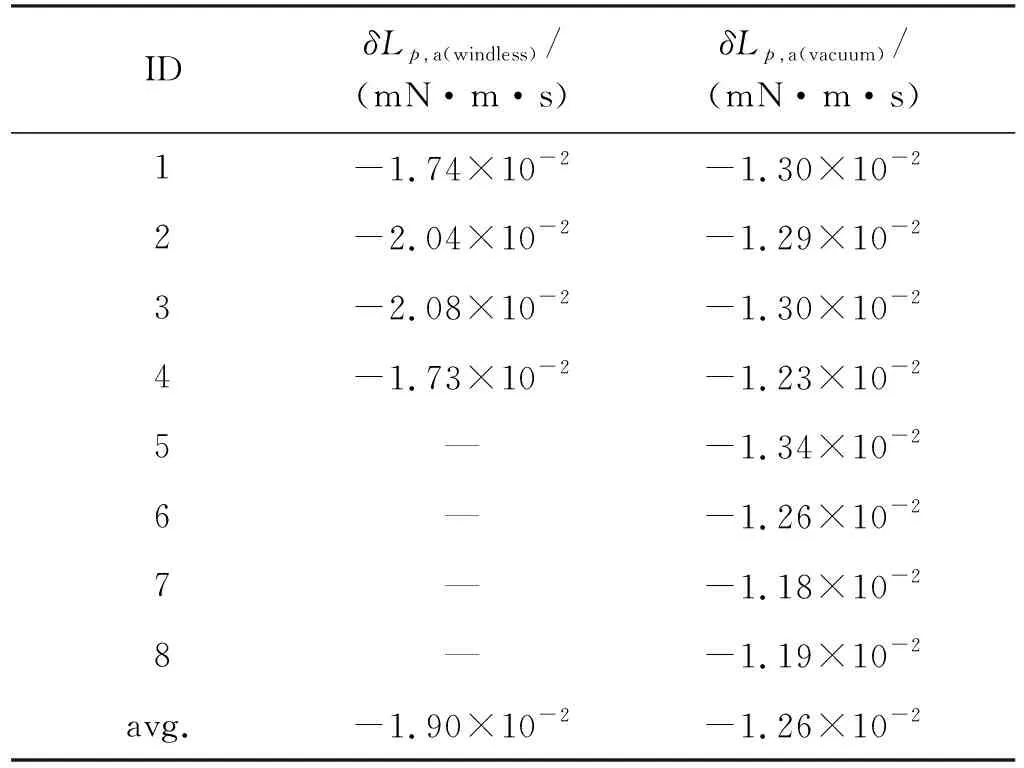
表2 附加滚转阻尼力矩无风和真空实验标定结果

表2中结果可见, 真空条件下气浮轴承滚转摩擦阻尼力矩要明显小于无风条件, 约为无风条件下的2/3, 原因在于真空条件下几乎没有外部空气的摩擦阻尼作用, 结果与前文的分析一致. 各条件下, 尤其是真空下标定值变化不大, 较稳定, 平均为 -1.26 × 10-2mN·m·s. 这一数值可作为该气浮轴承风洞实验时滚转阻尼力矩的测量偏差, 或直接予以扣除以减小这一偏差.

2.2 偏翼标模实验结果

本文以1.2°偏翼标模[7-8]为风洞实验研究对象, 实验名义Mach数为5.0, 总压P0=1×106Pa, 总温T0=353 K, 来流动压q=36 000 Pa. 实验结果在文献[8]中已给出, 并与文献[7]进行了对比, 如表3所示.

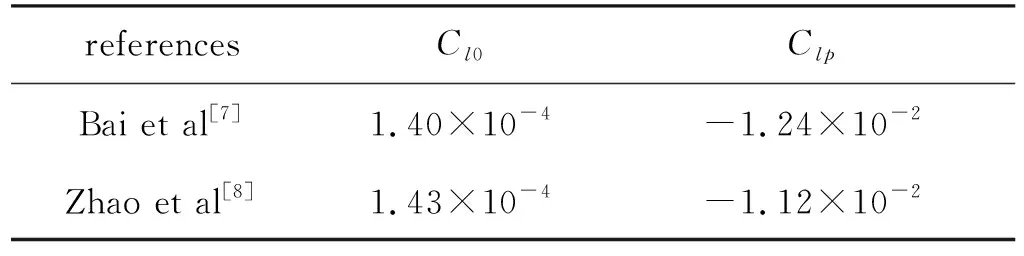
表3 标模实验结果

2.3 误差分析

首先, 考虑气浮轴承动态特性对测量结果的影响. 根据前文的气浮轴承标定结果,δL0,a和δLp,a分别采用低转速范围和真空下的标定平均值, 无量纲后为:δCl0,a=5.77×10-7,δClp,a=-8.82×10-4, 比实验结果低了多个量级, 验证了实验结果的可信度, 也说明该误差对于1.2°偏翼标模实验结果几乎可以忽略. 但对于测量对象量级较小时, 如某些烧蚀外形Cl0量级仅为10-5～10-6左右, 则需要酌情扣除气浮轴承的标定结果作为最终实验结果.

然后， 分析原始数据采集测量误差. 时间测量误差和角位移误差是与测量设备性能直接相关的误差, 可直接给出. 本文实验中采用光电计数器配合光栅孔的测量方式[8], 采样频率25 kHz, 可认为时间测量误差最大为δt=±0.04 ms.光栅孔的加工精度决定了角位移的测量误差, 一般取δθ=±0.05°.

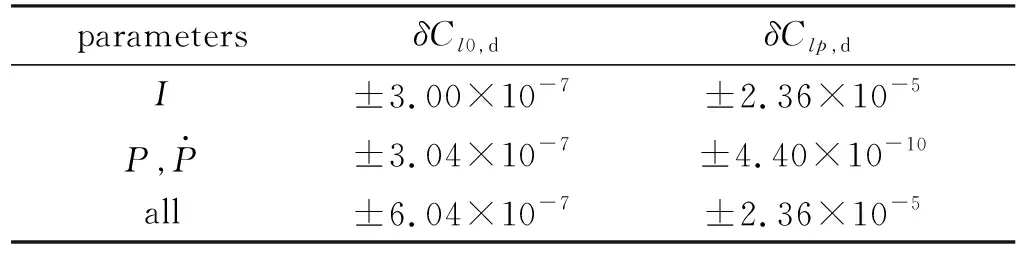
表4 拉偏参数辨识结果

表4中结果可见, 转动惯量测量误差对Clp结果影响较大, 综合来看测量误差带来的Clp误差为10-5量级, 远小于测量结果和气浮轴承标定结果量级, 可忽略不计. 综合测量误差带来的Cl0误差为10-7量级, 远小于测量结果量级, 与气浮轴承标定结果量级一致.

最后, 分析最小二乘法的参数辨识误差, 根据公式(7)～(9), 1.2°偏翼标模实验参数辨识时各系数计算结果如表5所示.

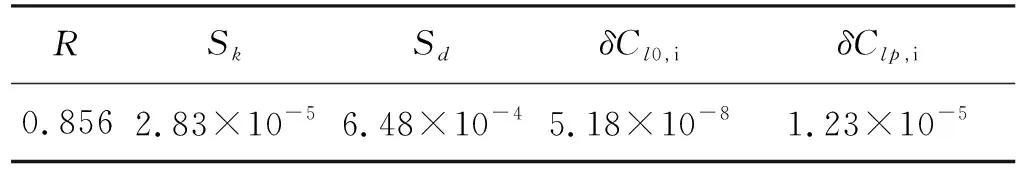
表5 参数辨识中各系数

表5中结果可见, 线性相关系数R=0.856, 说明原始数据线性相关程度较好, 辨识结果可信. 最终Cl0和Clp的最小二乘法辨识误差分别为10-8和10-5量级, 远小于测量结果量级, 相对于气浮轴承标定结果也低了约1个量级, 可忽略不计.

综上所述, 表6汇总了各类误差分析的无量纲结果, 同时也给出了常用再入飞行器研究对象如偏翼标模和烧蚀模型实验结果的大致范围作为对比.

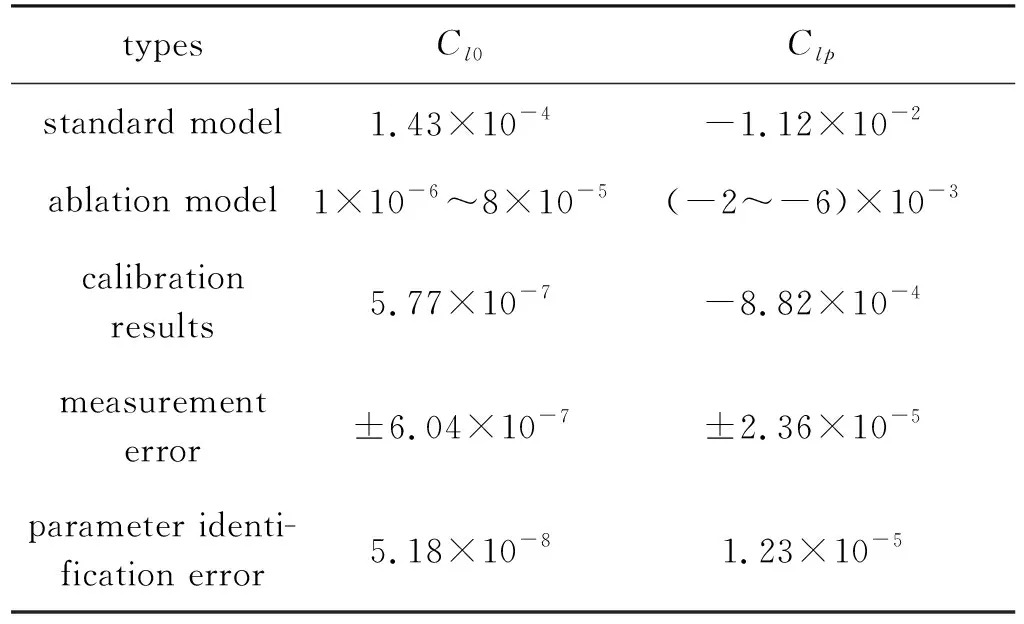
表6 结果汇总

根据表6中结果对比3种误差来源, 对于实验结果Cl0, 气浮轴承不对称附加滚转力矩和原始数据采集测量误差是主要误差来源, 参数辨识误差为高阶小量; 对于实验结果Clp, 气浮轴承摩擦阻尼是主要误差来源, 其他误差为高阶小量. 因此, 若研究对象是1.2°偏翼标模或类似带偏翼的模型, 上述误差均比实验结果小1～3个量级, 是高阶小量, 可忽略不计. 若研究对象为烧蚀等外形,Cl0和Clp较小、 与较大的误差来源差别不到1个量级, 建议扣除气浮轴承的标定结果并引入误差带作为最终实验结果, 可表示为

Cl0=Cl0,m-δCl0,a±δCl0,d

=Cl0,m-5.77×10-7±6.04×10-7

Clp=Clp,m-δClp,a=Clp,m+8.82×10-4

3 结论

本文以偏翼标模为研究对象进行了小滚转力矩测量, 并针对气浮轴承动态特性进行了研究, 进一步给出了测量误差分析结果, 研究表明:

(1) 气浮轴承动态特性对测量结果影响较小, 可视测量对象进行处理: 若为高阶小量, 可忽略不计, 量级相近可作为测量偏差予以扣除;

(2) 滚转力矩系数测量综合误差约为10-7量级, 主要来源是气浮轴承不对称附加滚转力矩和原始数据采集测量误差, 参数辨识误差是高阶小量可忽略; 滚转阻尼导数测量综合误差约10-4量级, 主要来源是气浮轴承摩擦阻尼, 原始数据采集测量误差和参数辨识误差是高阶小量, 可忽略.

致谢感谢李潜研究员在本文工作开展过程中给予的指导与帮助！