前缘形状对钝三角翼边界层稳定性及转捩的影响
2021-10-15马祎蕾梁伟栋王建林
马祎蕾, 余 平, 刘 璟, 梁伟栋, 王建林
(中国运载火箭技术研究院空间物理重点实验室, 北京 100076)
引 言
高速飞行器边界层流场发生转捩时, 飞行器气动特性及表面热环境均会发生显著改变, 正确预测转捩位置, 对飞行器设计与优化具有十分重要的工程意义[1]. 转捩诱因繁多, 触发机制复杂, 受到转捩Reynolds数、 攻角、 钝度、 边界层边缘Mach数等多重因素影响[1-4], 其中, 外形钝度是影响边界层流动稳定性的一个重要因素.
以往关于高速边界层转捩钝度影响的研究很多, 但多为针对钝度半径、 前缘曲率的研究, 文献[4]指出, 对于轴对称外形, 适度的端头钝度会显著地推迟转捩, 对于面对称的升力体外形, 适度的前缘钝度亦会显著地推迟转捩; Stetson等[5]通过地面试验发现在Mach数5.5的激波风洞中, 钝锥端头钝化可有效推迟转捩, 然而, 钝度一旦超过某一临界值, 转捩将提前, 出现“转捩反转”, 并在1984年发现这种转捩延迟效应与钝度带来的熵层有关, 存在“熵吞”现象[6]; Malik等[7]采用PNS方法研究发现钝度使边界层稳定. Rosenboom等[8]发现当钝度增加时第2模态临界Reynolds数单调增加, 但第1模态临界Reynolds数在大钝度和小钝度情况下单调性不同; Kara等[9]采用eN法, 将N=10作为转捩判据, 发现随着钝度增大, 转捩Reynolds数变大; 万兵兵等[10], 欧吉辉等[11]研究了钝度对激波后熵层基本流特性及熵层不稳定性的影响.
实际上, 除了钝度半径会影响转捩外, 钝度形状也是构成钝度的一部分, 据了解, 改变端头形状亦会对下游的边界层转捩产生影响, 选择合适的端头形状能够起到推迟转捩的作用, 然而, 这方面的资料相对很少. Lin等[12]研究发现前缘椭球比增大时, 边界层内被激发的T-S波幅值减小, 反之幅值增大; Lin等[13]研究发现, 前缘顶端曲率可通过前缘Reynolds数影响边界层流动稳定性; 沈露予等[14]通过DNS方法研究了自由来流湍流下不同椭前缘形状的平板边界层感受性问题.
目前, 对高速边界层常用的转捩预测方法主要有3类: 转捩准则、 转捩模式法与eN法, 其中eN法[15-17]的理论基础即线性稳定性理论(linear stability theory, LST), 并最大限度地利用了边界层扰动演化的理论预测[18-19]. 尽管其忽略了边界层的感受性、 非线性作用等因素, 仍被Cebeci等波音工程师认为是最有效的转捩预测方法.
考虑到采用升力体外形的高速飞行器, 多包含钝化的端头和翼前缘、 大后掠角的翼面形状及较为扁平的迎风面构型等, 三维几何特征明显, 因此, 本文选择平板钝三角翼外形, 围绕典型高速风洞实验状态开展流场数值计算和线性稳定性分析, 并采用eN法获取表面N值分布进行转捩预测, 研究在LST理论背景下, 不同椭前缘形状对边界层流动稳定性特征的影响, 并探究前缘钝度形状对边界层转捩的影响.
1 计算方法
1.1 数值计算方法
N-S方程数值求解中, 采用有限体积法, 对流项采用3阶迎风Roe-FDS格式离散, 黏性项采用中心差分格式离散, 时间推进为AF-LU隐式方法.
不考虑对底部流场的模拟, 物面采用无滑移边界条件, 出口设为超声速外插边界条件. 计算域为半模, 经网格收敛性验证, 确定网格量为221×241×351, 如图1所示, 法向网格布置点数较多, 原因在于后续稳定性分析需要较为精细的边界层流场.
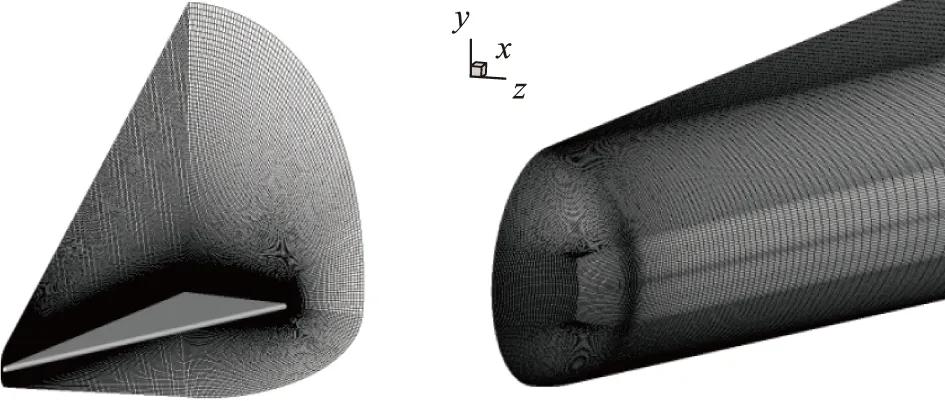
图1 计算域及网格Fig. 1 Computational domain and meshes
1.2 稳定性计算方法
根据线性稳定性理论, 二维局部平行流假设下, 分析O-S方程可将小扰动q表示为行进波形式

(1)
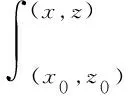
(2)
式中, (x0,z0)为频率为ω的扰动波开始失稳处(αi,βi由正转为负), 其位置在中性曲线上; 增长率-αi, -βi取当地频率为ω的最不稳定扰动波(增长率最大)的增长率, 扰动传播路径方向即该扰动波的群速度方向, 由于群速度方向与势流方向非常接近, 本文采用势流方向作为扰动波增长率积分方向.
预设转捩判据为Ntr(通常由经验给出), 即对于不同频率ω的扰动波, 若在(xtr,ztr)处幅值放大因子达到Ntr, 预示转捩发生. 不同频率扰动波扰动幅值达Ntr的位置不同, 一般取最上游位置作为转捩发生位置, 对应N值称为包络N值. 转捩位置曲线应满足
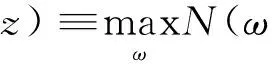
(3)
1.3 算例验证
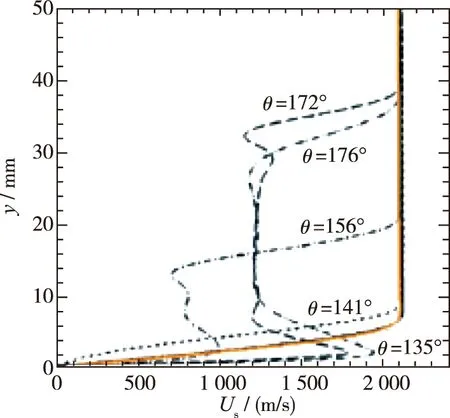
文献[20]针对HIFiRE-1飞行工况进行了数值模拟, 钝锥半锥角7°, 头部半径2.5 mm, 计算工况见表1.
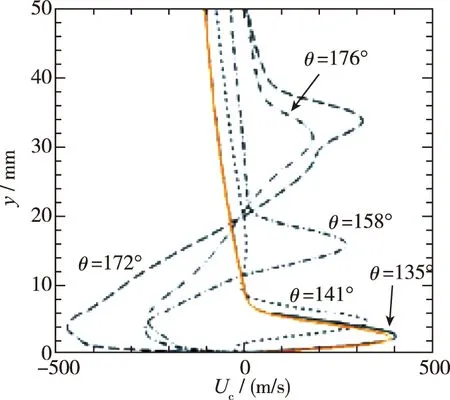
为考核三维流场计算的可靠性, 特别是边界层流场和横流效应, 本文采用目前的方法也进行了计算, 计算所得流向x=850 mm, 背风面θ=135°位置点的基本流速度剖面与文献[20]结果比较如图2所示, 其中橘色速度剖面为计算结果, 与算例基本相符, 验证了边界层流场计算的正确性.

表1 算例工况
(a) Streamwise velocity
(b) Crossflow velocity
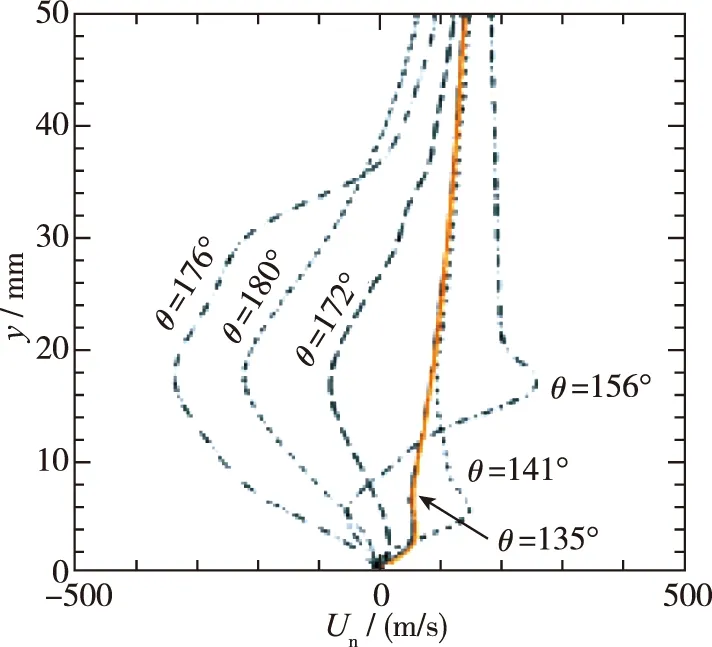
(c) Wall-normal velocity图2 算例对比Fig. 2 Comparison of numerical examples
2 几何模型与计算工况
几何模型为一平板钝三角翼外形[21], 长度取400 mm, 钝度半径3 mm, 后掠角75°. 定义坐标系原点O为钝三角板顶点,x,z轴指向如图3(a)所示,y轴符合右手坐标系.
定义椭圆前缘截面的长短轴比为形状因子m, 则m=a/b(如图3 (c)所示), 保持端头钝度半径为3 mm, 即保持b恒为3 mm, 分别改变前缘形状因子为0.5, 1和2, 以m050,m100和m200表示. 图3(b)为m200外形迎风面示意图, 图3(c)为(b)中m-n截面上3种前缘形状的椭圆截面分布.
根据静风洞实验结果, 选取典型风洞实验状态(如表2所示)为计算工况.

(a) Model and coordinate system
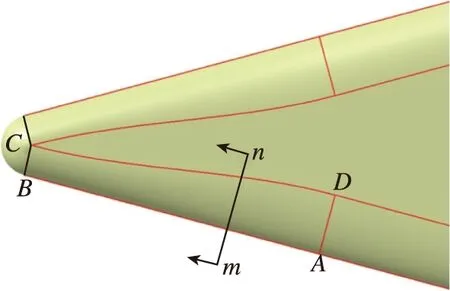
(b) Windward side of m200
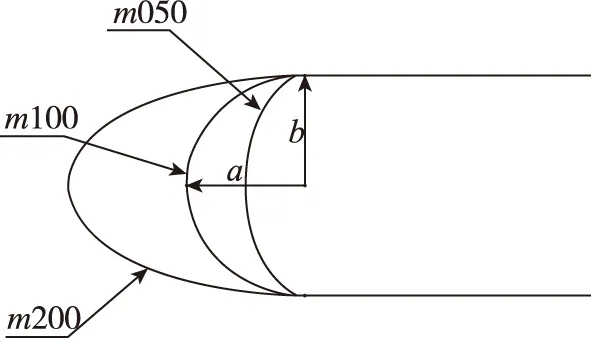
(c) m-n图3 平板钝三角翼外形及坐标系示意图Fig. 3 Model and coordinate system of flat-plate blunt delta wing

表2 计算工况
3 椭前缘形状影响分析
3.1 基本流分析
图4(a), (b)分别为m100前缘钝三角翼不同流向位置处Mach数分布图, 其迎、 背风边界层均从前缘向中心逐渐增厚, 并在对称中心线附近出现流向涡结构, 有攻角状态下, 迎风面流场特征相对简单, 流向涡尺度明显小于背风面, 故本文仅对迎风面进行分析.
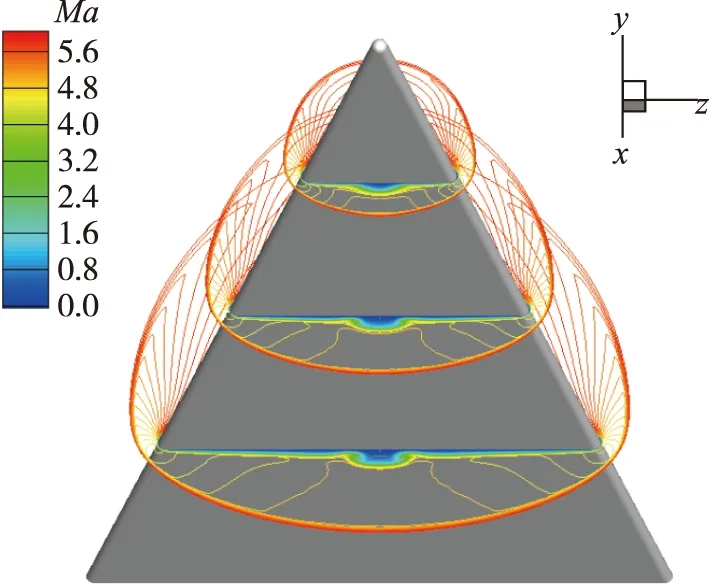
(a) Windward side
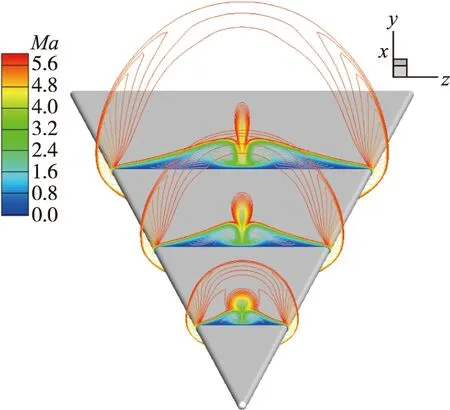
(b) Leeward side图4 不同流向位置Mach云分布Fig. 4 Mach number contours at different streamwise locations
定义最大横流速度为沿法向分布的横流速度最大值, 以来流速度U∞= 860.838 m/s对横流速度无量纲化, 则迎风面最大无量纲横流速度分布如图5所示. 可知正攻角工况下, 钝三角翼流向前部, 靠近前缘位置处最大横流速度较大; 沿流向发展, 前缘处最大横流速度逐渐减小; 同一流向位置截面上, 展向中间区域(去除前缘和中心区域)最大横流速度较大.
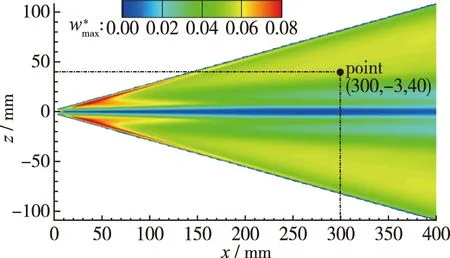
图5 迎风面最大横流速度分布Fig. 5 Distribution of maximum cross flow velocity on windward surface
由于中心流向涡结构区域流动复杂, 流场变化剧烈, 因此, 采用线性稳定性理论分析时应避开该区域. 故基于m100钝三角翼外形, 特别是中心流向涡尺度特征和边界层横流流动特征, 选择横流效应相对较强, 位于展向中间区域的point(300,-3,40)作为典型点, 来分析不同前缘形状对钝三角翼不同模态流动稳定性特征影响.
图6为不同前缘形状模型流向x=300 mm的迎风面边界层厚度分布, 边界层厚度由总焓确定, 为由壁面开始过峰值后等于来流总焓的1.005倍位置处[10]. 分析可知前缘形状仅对前缘区域边界层厚度产生影响, 翼身区域的边界层厚度线性分布区域基本相同.
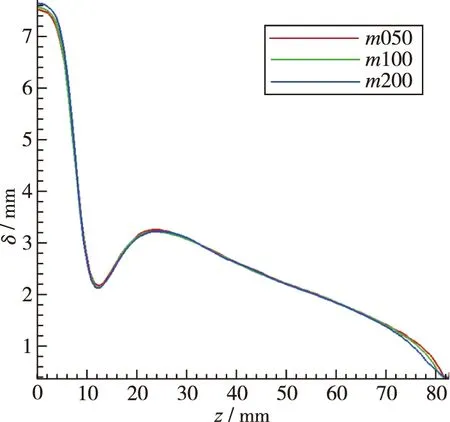
图6 x=300 mm边界层厚度Fig. 6 Boundary layer thickness at x=300 mm
不同前缘形状三角翼外形的迎风面最大横流速度分布云图见图7(a)~(c), 可知前缘形状主要影响钝三角翼流向前部, 靠近前缘的具有强横流效应区域, 且前缘形状越尖, 最大横流速度越大, 具有较强横流效应区域越广; 前缘形状对三角翼翼身最大横流速度分布影响较小.
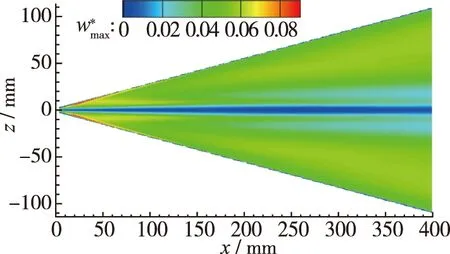
(a) m050
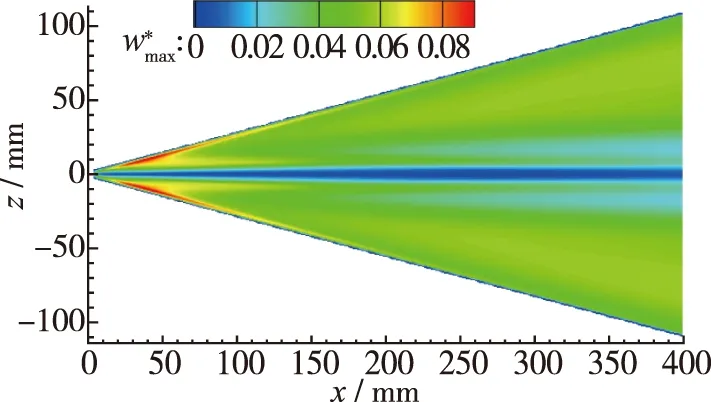
(b) m100
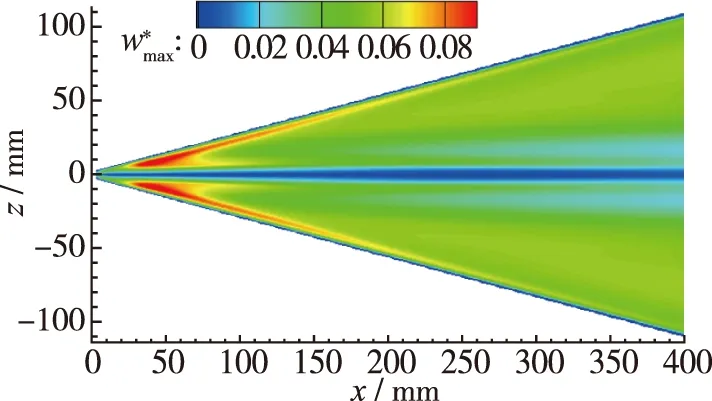
(c) m200图7 迎风面最大横流速度Fig. 7 Distributions of maximum cross flow velocity
3.2 稳定性分析
由图5, 6可知, point(300,-3,40)位于展向40 mm处, 不在中心流向涡影响区域内, 故可作为后续线性稳定性特征分析点.
具有不同椭前缘截面形状外形过point点的边界层外缘势流方向如图8(a)所示, 势流方向基本重合. 图8(b)~(d)分别为m050,m100和m200 这3种外形沿该势流方向不同频率扰动波增长率分布曲线.
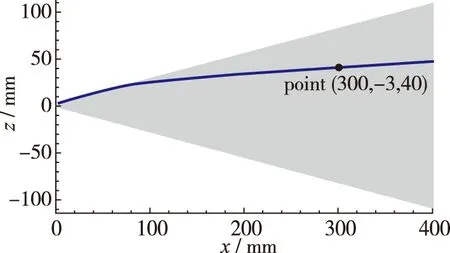
(a) Streamline passing point 2

(b) m050

(c) m100
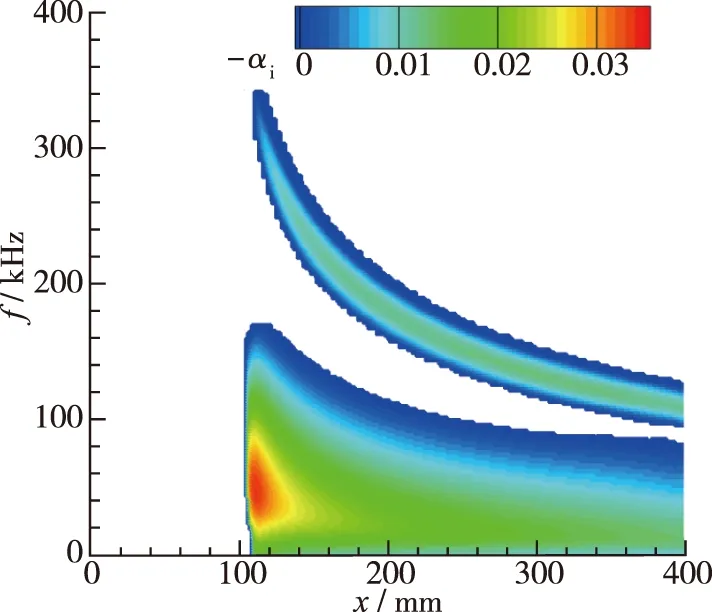
(d) m200图8 势流方向与增长率沿势流分布Fig. 8 Streamline and streamwise distribution of grouth rate
比较可知, 不同前缘形状主要影响失稳起始区域(前缘附近区域)的稳定性特征分布, 形状越尖, 前缘附近第1模态增长率越大, 而势流方向下游远离前缘区域的第1模态增长率分布基本相同; 第2模态增长率则随着前缘变尖而逐渐增大. 前缘形状对不同模态开始出现扰动增长的流向位置产生不同影响, 前缘越尖, 第1模态的流向(x向)中性点位置越靠后, 第2模态的中性点位置则略微前移.
选取f=0 kHz(横流驻波), 30 kHz(第1模态)和200 kHz(第2模态)3条扰动波, 其增长率沿图8(a)中的势流方向的分布如图9所示. 分析可知, 同一频率扰动波沿势流方向发展, 前缘形状不同, 增长率在前缘的分布完全不同.
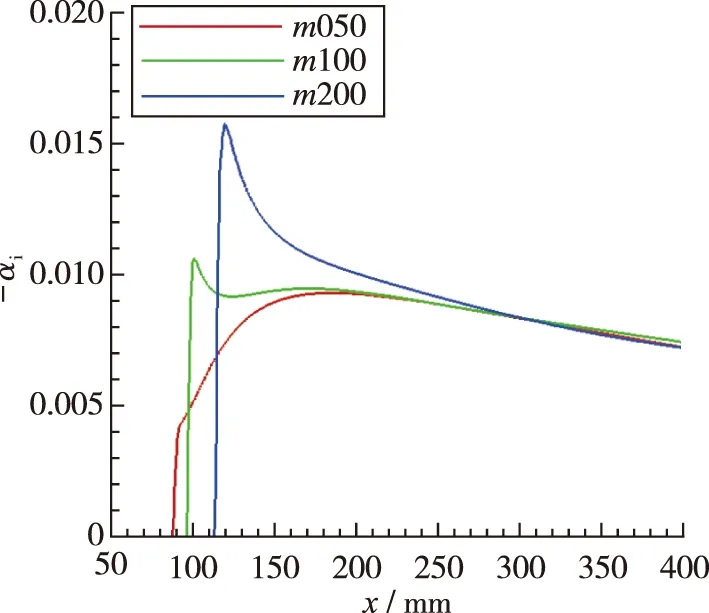
(a) f=0 kHz
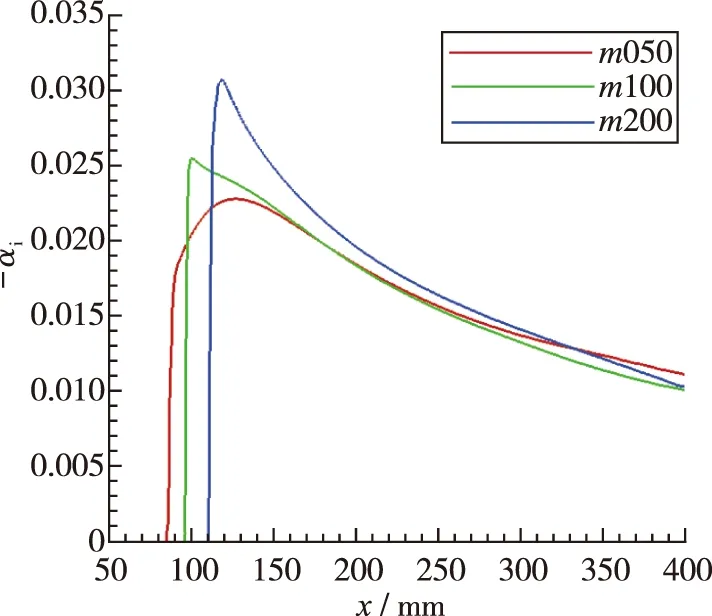
(b) f=30 kHz
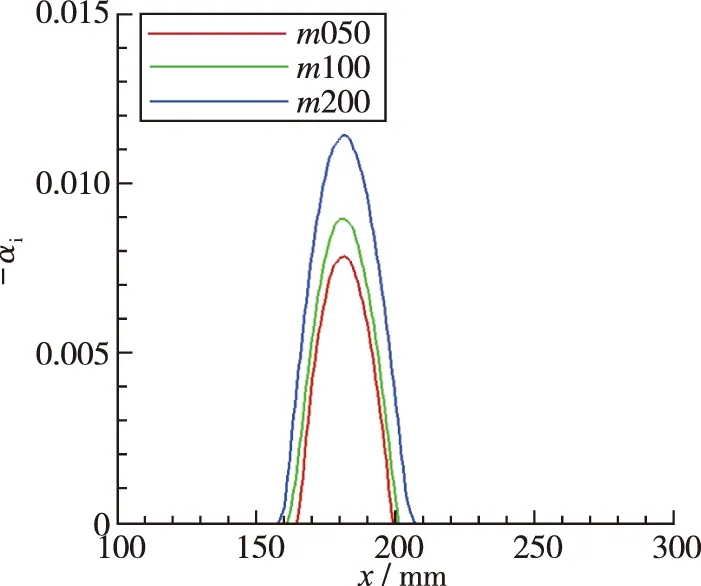
(c) f=200 kHz图9 增长率分布Fig. 9 Distributions of growth rate
图9(a)为横流驻波(f=0 kHz), 前缘较尖时(m200), 横流效应强, 前缘处横流驻波增长率大, 导致增长率沿势流方向出现局部峰值点, 随后缓慢降低, 而前缘较钝时(m050), 从前缘过渡到翼身区域, 横流驻波增长率平缓增长再下降, 未出现增长率局部峰值点; 图9(b)f=30 kHz扰动波在不同前缘形状的增长率分布趋势与f=0 kHz类似, 但增长率幅值差异有所降低; 以图9(c)f=200 kHz 表征第2模态增长率分布, 则前缘变尖, 增长率变大, 同时中性点位置略微前移.
3.3 转捩预测
目前工程上对于T-S波转捩与横流转捩同时存在的情况, 将取两个不同的转捩N值, 即NTS,tr与NCF,tr, 再分别积分NTS与NCF, 二者之一达临界值时即预示转捩发生[22]. 本文将NTS,tr与NCF,tr取为同一个值, 并统一归至第1模态进行转捩预测.
如图10所示, (a)为包括横流模态的第1模态包络N值分布, (b)为第2模态包络N值分布. 显然, 第1模态N值远高于第2模态, 即迎风面转捩为第1模态导致. 经与静风洞温敏漆转捩测量结果对比, 转捩位置处Ntr约为3. 上文中点point位于转捩区域, 作为参考, 该位置处N值约为4, 失稳波频为30 kHz, 为第1模态失稳.
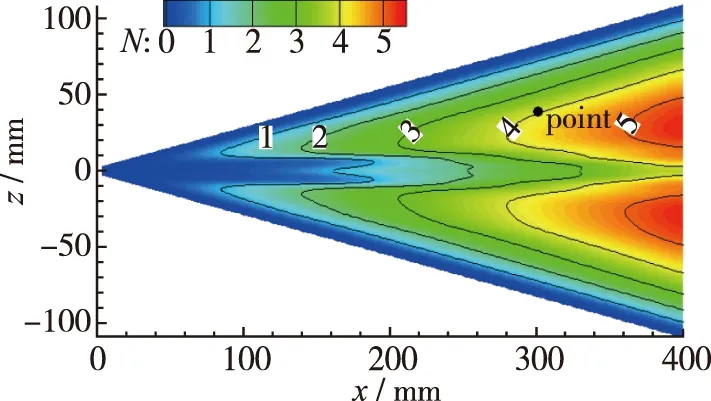
(a) First modes(f=0~76 kHz)

(b) Second modes(f=77~328 kHz)图10 不同模态包络N值分布Fig. 10 N-factor contours for different mode disturbances
图11(a)~(c)分别为不同椭前缘外形, 频率f=0, 30, 200 kHz扰动波N值沿势流方向分布. 由图可知, 随着前缘变尖,f=0 kHz扰动波出现一定量值后同一N值的流向位置逐渐前移, 频率f=30 kHz 的扰动波出现一定量值后同一N值的流向位置逐渐后移, 如表3所示为该扰动波的N值达到转捩N值(Ntr=3)的流向坐标, 而频率f=200 kHz的扰动波N值随着前缘变尖而增大.

(a) f=0 kHz
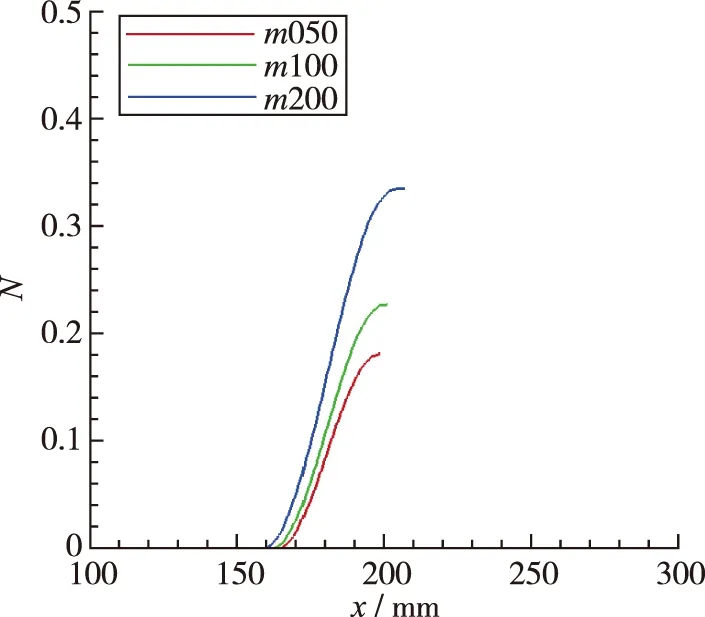
(c) f=200 kHz图11 N值分布Fig. 11 Distributions of N-factor

表3 f=30 kHz扰动波Ntr=3流向位置
结合图9可知, 不同椭前缘截面形状外形, 前缘处增长率差异较大, 同时沿势流方向不稳定区域长度(积分区间)也不同, 前缘越尖增长率越大, 但相应扰动中性点越靠后, 积分区间越短, 而N值是增长率沿势流方向积分的结果, 故f=0 kHz时增长率起主导作用, 前缘变尖加速失稳,f=30 kHz时增长率差异小, 积分区间起主导作用, 前缘变尖积分区间变短, 可推迟转捩. 即前缘形状变尖, 将抑制第1模态失稳, 促进横流模态和第2模态失稳.
不同椭前缘截面形状外形的转捩阵面(Ntr=3)如图12所示. 3种外形均为第1模态转捩, 沿展向呈“M型”分布, 随着前缘形状变尖, 流向转捩位置逐渐后移, 展向转捩位置几乎无变化.

图12 转捩阵面Ntr=3Fig. 12 Transition locations at Ntr=3
4 结论
本文研究了在典型风洞实验状态(Re∞= 3×106,Ma∞= 6,α= 10°)下, 不同椭前缘截面形状对迎风面平板钝三角翼高速边界层流动稳定性及转捩的影响, 所得结论如下:
(1)前缘形状将影响前缘附近区域边界层流场特征, 对远离前缘区域影响较小, 且前缘形状越尖, 横流速度越大.
(2)前缘形状对不同模态影响不同: 前缘形状变尖, 一定频率的第1模态和横流模态扰动波的中性点位置后移, 扰动增长率变大; 一定频率的第2模态扰动波增长率变大, 中性点位置基本不变.
(3)由静风洞实验结果标定, 本计算工况下转捩N值Ntr=3, 转捩预测结果为第1模态导致转捩; 随着前缘形状变尖, 受第1模态中性点位置后移影响, 流向转捩位置逐渐后移, 展向失稳位置几乎不变.
