辐射平衡壁温下有限催化模型数值模拟

莫 凡, 王锁柱, 高振勋

(1. 北京航空航天大学航空科学与工程学院, 北京 100191;2. 北京航天长征飞行器研究所, 北京 100076)

引 言

高超声速飞行器在大气中进行高Mach数飞行时, 来流经过头部脱体激波的剧烈压缩后往往能达到很高的温度[1], 导致高温空气中发生复杂的化学反应. 一般情况下, 在2 500 K以上空气中的氧气开始离解, 4 000 K以上氮气开始离解, 而到9 000 K以上氧原子和氮原子将进一步电离.

当离解之后的高温空气到达飞行器表面时, 表面材料会对空气中的原子和离子产生显著的催化复合作用, 这种催化复合作用将改变飞行器壁面附近各组分的质量分数梯度分布, 引起流场中输运特性的改变, 进而显著改变壁面热流密度的分布. 已有研究表明, 在高Mach数情况下关键部位防热材料表面的催化复合效应最高将带来近50%以上的气动热载荷[2]. 因此在CFD模拟中, 催化边界条件的确定往往非常重要, 完全非催化(non-catalytic wall, NCW)和完全催化(full-catalytic wall, FCW)[3]是高超声速飞行器气动热环境数值模拟中最常用的两种催化边界条件. 完全非催化假设壁面催化复合速率为0, 即壁面组分质量分数的梯度为0. 而完全催化一般假设壁面来流原子的离子在壁面完全复合, 此时壁面组分质量分数的梯度也将最大.

然而, 以上两种组分边界条件均不能反映实际发生的壁面催化过程, 实际飞行中均为有限催化情况, 因此必须使用有限催化[3](finite-rate catalysis, FRC)边界条件才能反映真实的壁面催化效应, 该边界条件的关键在于催化复合系数的取值. 粟斯尧等[4]选取了催化复合系数为常数的有限催化边界条件, 针对类联盟号飞船返回舱外形研究了气动热环境随壁面催化效率的变化规律, 并对壁面有限催化影响气动加热的物理机制进行了探讨. 丁明松等[5]开展了在有限催化条件下, 表面材料催化特性差异性对热环境的影响, 得出壁面催化复合系数的差异性会带来局部热流的跳变, 使局部区域热流明显高于全表面催化复合系数为0.1的情况, 且壁面复合系数差异越大, 热流跳变的程度越大. 然而对于实际的高超声速飞行器表面催化效应, 其表面的复合系数取常数是不恰当的. Inger[6]的实验表明催化复合系数往往与壁面材料和壁面温度有关, 并给出了某碳基材料催化复合系数随表面温度变化的拟合公式. Scott[7]开展了典型材料的催化复合系数研究, 并给出了2 000 K以下大部分碳基和硅基热防护材料催化复合系数小于0.1的结论. Scott[8]和Zoby等[9]分别给出了实验和飞行数据修正后氧原子和氮原子催化复合系数随温度拟合的公式. 国内关于采用温度拟合催化复合系数研究有限催化的工作尚少, 董维中等[10]采用源于实验数据拟合得到的与壁温相关的O原子的催化复合系数, 开展了辐射平衡表面温度分布与气动热的耦合计算, 但由于未考虑氮原子的催化复合效应, 因此模型并不完整.

本文在现有考虑离子组分的有限催化边界条件的基础上, 引入了由温度拟合得到的氮氧原子催化复合系数, 研究了在辐射平衡壁温下有限催化模型对典型再入高超声速飞行器气动热环境的影响规律. 文中首先给出了流动控制方程及有限催化边界条件的数学形式, 在此基础上建立了高超声速飞行器化学非平衡流场有限催化气动热环境数值计算方法及程序, 并通过与风洞实验气动热结果对比验证了数值模拟结果的可靠性. 在此基础上考虑到有限催化中催化复合系数与壁面温度相关, 采用了Scott和Zoby给出的氧原子和氮原子催化复合系数随温度拟合的公式, 并研究钝锥外形在辐射平衡壁温下有限催化对壁面热环境的影响规律.

1 计算方法

1.1 化学非平衡流动的瞬时N-S方程

在Descartes坐标系下, 含化学反应流动的瞬时N-S方程可写成如下守恒形式

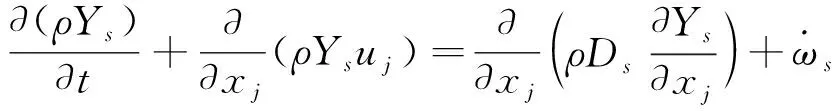
(1)

式中,ρ,ui,p,T分别为气体的密度、 速度、 压强与静温;E为单位(体积)质量总能量

(2)

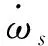
(3)

其中，μ为混合气体的分子黏性系数. 各组分分子黏性系数、 热传导系数、 质量扩散系数等输运系数和比热、 比焓均采用Gupta的拟合公式得到[11], 而空气混合物整体的输运系数则根据Wilke的公式计算得到[12].

1.2 数值求解方法

在对方程(1)无量纲化处理后, 采用有限差分方法进行离散, 其中对流项采用Roe格式离散, 并采用Harten-Yee型熵修正, 且熵修正系数取0.25, 黏性项采用2阶中心差分离散. 时间推进上为提高CFL步长以及求解的稳定性, 采用LU-SGS隐式方法, 并采用当地时间步长加速收敛. 对于三维复杂多块结构网格, 采用MPI分区并行求解技术以提高计算效率.

1.3 有限催化边界条件

在高超声速化学非平衡流动的CFD模拟中, 壁面催化效应通过壁面边界条件影响对应的控制方程的解. 下面以7组分电离空气为例, 给出了包含离子在内的组分质量分数边界条件.

对于包含离子组分的高温气体, 在壁面上发生的催化复合反应主要有两类, 即原子的复合和离子的复合. 现仅考虑以下3个催化复合反应

N+N→N2; O+O→O2; NO++e-→NO

(4)

有限催化壁边界条件一般通过求解壁面附近质量守恒方程的方法构建. 不考虑质量引射时, 气体组分由催化反应生成(或消耗)的质量与扩散出(或入)壁面微元的质量相等.

由催化反应引起的单位时间, 单位面积壁面上各组分质量消耗(生成)率为

(5)

其中，kws为反应速率常数. 假设壁面原子服从Maxwell-Boltzmann分布, 则kws与壁面催化复合系数γs具有如下关系[13]

(6)

式中,R0为普适气体常数;Tw为壁面温度;Ms为组分s的摩尔质量. 壁面催化复合系数γs表示壁面发生催化复合的原子数与入射到壁面总原子数之比. 其取值范围在0到1之间, 取0时表示完全非催化(NCW), 取1时表示完全催化(FCW), 取0到1之间则为有限催化(FRC).

另一方面, 由Fick定律得壁面处由扩散作用产生的质量通量为

(7)

其中，n为壁面法向单位矢量, 方向由壁面指向流场内部. 根据质量守恒定律, 各组分单位时间单位面积由催化反应产生(消耗)的质量与扩散出(到)壁面的质量应相等, 即各组分在壁面处的净质量通量为零. 故下述关系式成立

(8)

式(7)中存在导数项, 在CFD计算时需对其进行恰当的离散, 本文中消耗组分(s=O,N,NO+)采用以下离散方式

(9)

整理得

(10)

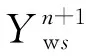
(11)

整理得

(12)

1.4 辐射平衡壁温边界条件

辐射平衡模型依据的主要原理是在壁面处能量守恒. 飞行器壁面一方面要接收流场的热流(壁面热流密度)Qflux, 另一方面要向内部结构传热Qinside, 另外还要通过电磁辐射向外发射能量(灰体辐射能量)Qradiation.当流场处于平衡状态时, 上述3种能量的传输也应满足以下的平衡方程

Qflux=Qinside+Qradiation

(13)

现对结构的内部传热忽略不计, 平衡方程则可以进一步化简为

Qflux=Qradiation

(14)

即流场向壁面的传热量应与壁面出射的辐射能量达到平衡. 当流场气体考虑组分时, 壁面热流密度可以表示为对流项热流密度Qconv和组分扩散项热流密度Qdiff之和,可由式(15)进行计算

(15)

其中,n代表壁面的法向方向,ρ为壁面流场密度,ns为气体组分个数,Ds代表组分s的扩散系数,hs是组分s的绝对焓,Ys代表组分s的质量分数.

若将壁面视为发射率等于ε的灰体, 则壁面出射的辐射能根据Stefan-Boltzmann定律, 可以写作

(16)

其中,σ为Stefan-Boltzmann常数, 取值为σ=5.67×10-8W/(m2·K4);Tw为壁面温度. 联立式(13), (15), 并将Qflux离散化, 则最终可得平衡方程

(17)

其中,T1和Tw分别为第1层网格和壁面处的温度;Ys1和Ysw分别为第1层网格和壁面处组分s的质量分数; Δy为第1层网格与壁面间的距离. 求解式(17)采用了Newton迭代法, 迭代关系如式(18)所示

(18)

2 等温壁有限催化计算

卡尔斯本大学巴法罗研究中心(CUBRC)利用LENS系列激波风洞对标模返回舱进行了一系列的研究[14]. 其中几何尺寸如图1所示, 实验工况如表1所示. 根据实验来流静温和Mach数可计算得到来流总温超过8 000 K, 因此采用了Gupta 5组分6反应化学反应动力学模型, 壁面上仅考虑O原子和N原子的催化复合反应. 计算网格如图2所示. 为了更好地捕捉头部脱体激波, 在返回舱头部前体附近对网格加密至0.2 mm.

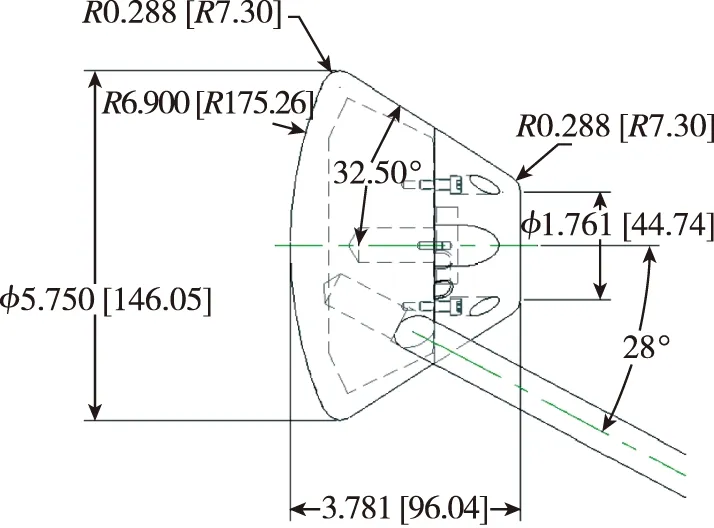
图1 返回舱模型几何尺寸(单位： in[mm])Fig. 1 Geometric dimensions of re-entry capsule model(unit: in[mm])

表1 返回舱实验工况

LENS激波风洞实验给出了标模返回舱对称面壁面上测量点的压力与热流测量值. 针对Test-1的CFD计算中组分边界条件采用完全催化(FCW)、 完全非催化(NCW)以及γ分别取0.015和0.1的有限催化(FRC), 在图3中与实验热流进行了对比. 由于催化效应几乎没有改变壁面的压强分布, 因此压强曲线在图2中仅给出一条并与实验结果对比.

针对 Test-2的CFD 计算中组分边界条件采用完全催化(FCW)、 完全非催化(NCW)以及γ取0.005 的有限催化(FRC), 在图4中与实验壁面热流及压强进行了对比. 图5给出了壁面的压强分布云图. 图6～8分别给出了完全非催化, 有限催化和完全催化边界条件下的热流密度分布云图.

从Test-1与Test-2的CFD计算结果可以得到壁面热流密度分布QFCW>QFRC>QNCW.这与以往经验和其他文献结论相符.

图2 返回舱模型计算网格Fig. 2 Three-dimensional structural grids for capsule geometry

图3 Test-1返回舱壁面热流与压强分布Fig. 3 Heat flux and pressure distribution on the capsule wall in Test-1

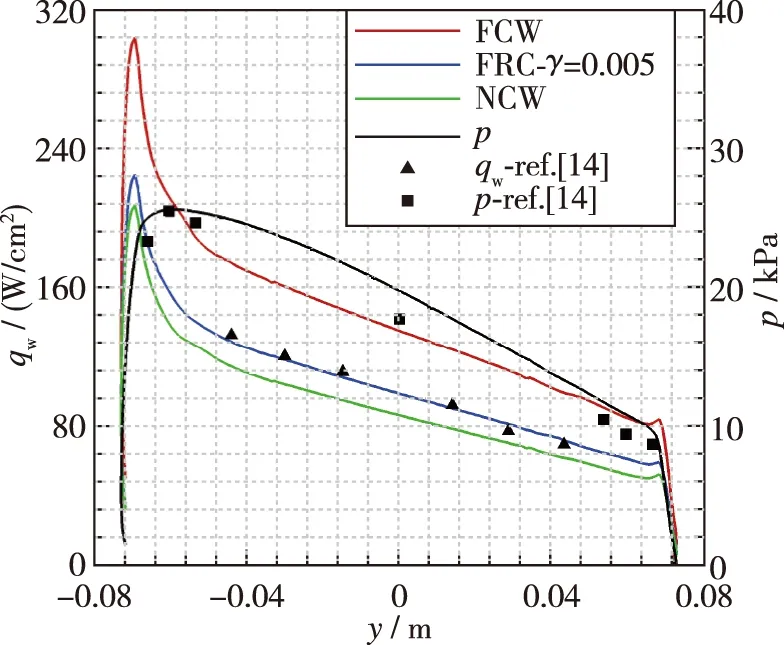
图4 Test-2返回舱壁面热流与压强分布Fig. 4 Heat flux and pressure distribution on the capsule wall in Test-2

图5 Test-2返回舱壁面压强分布云图Fig. 5 Contour of pressure on the capsule wall in Test-2

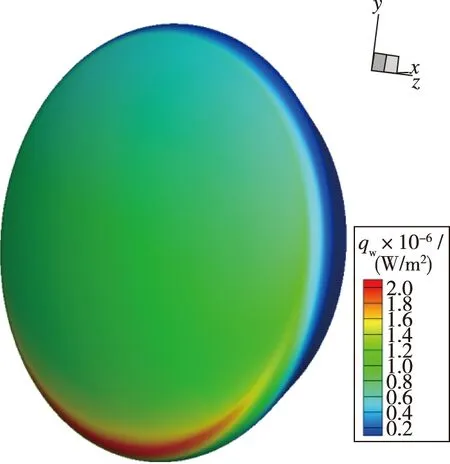
图6 Test-2返回舱壁面完全非催化热流密度分布云图Fig. 6 Contour of heat flux at the NCW in Test-2

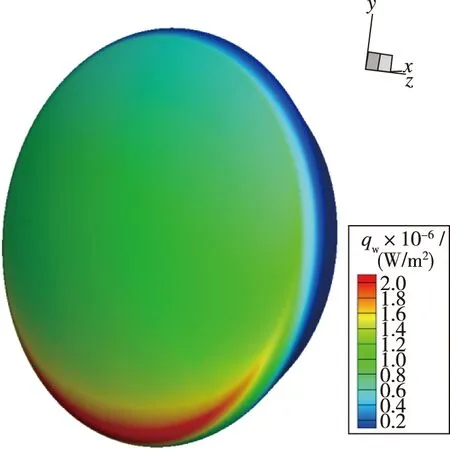
图7 Test-2返回舱壁面有限催化热流密度分布云图Fig. 7 Contour of heat flux at the FRC in Test-2

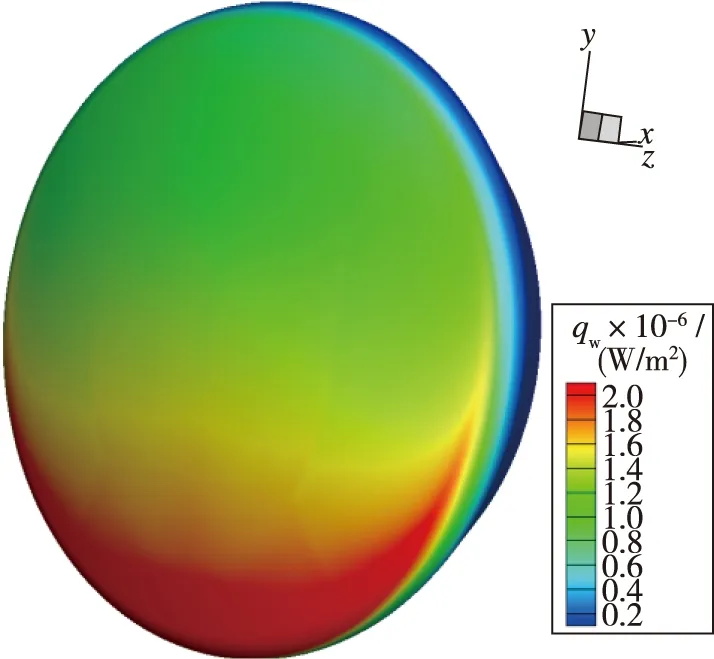
图8 Test-2返回舱壁面完全催化热流密度分布云图Fig. 8 Contour of heat flux at the FCW in Test-2

而在使用有限催化模型时, 当催化复合系数γ取合适值时可以得到与实验结果更加吻合的结果. 这从侧面反应了高超声速化学非平衡流动的壁面催化反应是有限催化, 与以往人们的观点相符. 此外, 当催化复合系数γ取0时, 组分质量分数边界条件自动退化为完全非催化壁条件.

由图9分析Test-1壁面热流组成可得, 壁面热流由热传导引起的热流和各组分质量扩散引起的热流组成, 且在本算例中热传导引起的热流大于各组分质量扩散引起的热流. 在质量扩散引起的热流中, 氧原子质量扩散引起的热流密度占主要成分, 其他组分(如氮原子)仅仅占很小一部分, 这与各组分质量分数在壁面的梯度有关. 以氧原子和氮原子为例, 如图10所示, 由于激波后静温不到7 000 K, 氮气分子离解程度远小于氧气分子, 因此在壁面处氮原子质量分数梯度远小于氧原子质量分数梯度, 进而由氮原子质量扩散引起的热流密度小于氧原子质量扩散引起的热流密度.

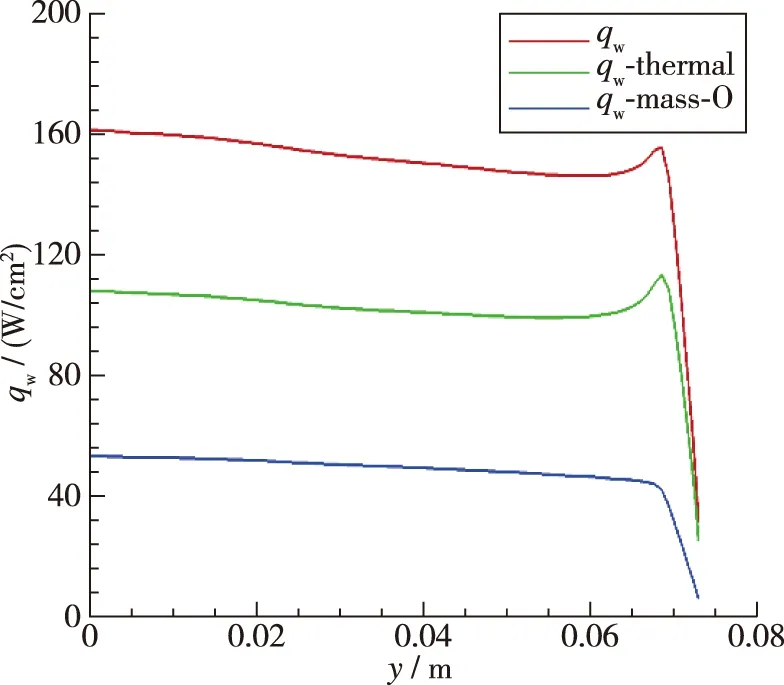
图9 Test-1返回舱壁面热流组成Fig. 9 Composition of the heat flux in Test-1

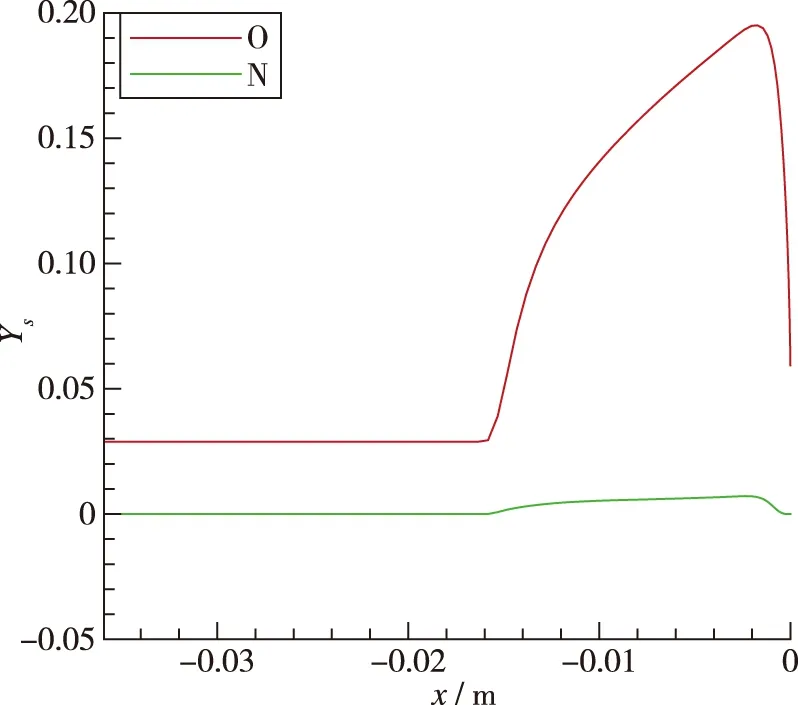
图10 Test-1有限催化驻点线氧原子和氮原子质量分数分布图Fig. 10 Mass fraction distribution of oxygen and nitrogrn along the stagnation line at the FRC in Test-1

图11～12给出了Test-1有限催化氧分子沿驻点线质量分数分布, 可得壁面氧原子质量分数下降, 氧气上升, 表明在催化边界的作用下, 氧原子在壁面复合为氧气. 完全催化的复合程度最大且壁面氧原子质量分数降到接近于0, 小于来流的氧原子质量分数.

完全非催化条件下, 氧原子质量分数在壁面也有一定程度的降低. 这是由于壁面温度仅有300 K, 激波后到壁面之间温度逐渐下降, 在壁面附近温度急剧下降, 而温度影响了化学反应速率进而使当地流动趋向于新的化学平衡, 因此由激波后高温离解产生的原子在壁面附近自动复合.

由以上可以更清晰地得出, 壁面复合效应有两个组成部分, 第一是由壁面材料催化直接导致的复合, 第二是由壁面附近低温导致的化学反应速率变化而间接引起的复合.

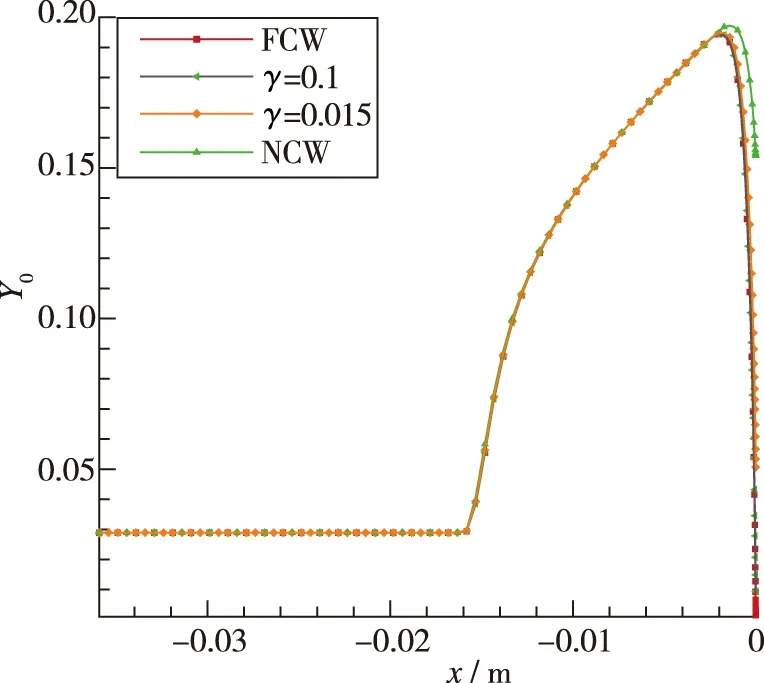
图11 Test-1有限催化氧原子沿驻点线质量分数Fig. 11 Mass fraction distribution of oxygen along the stagnation line at different catalytic conditions in Test-1

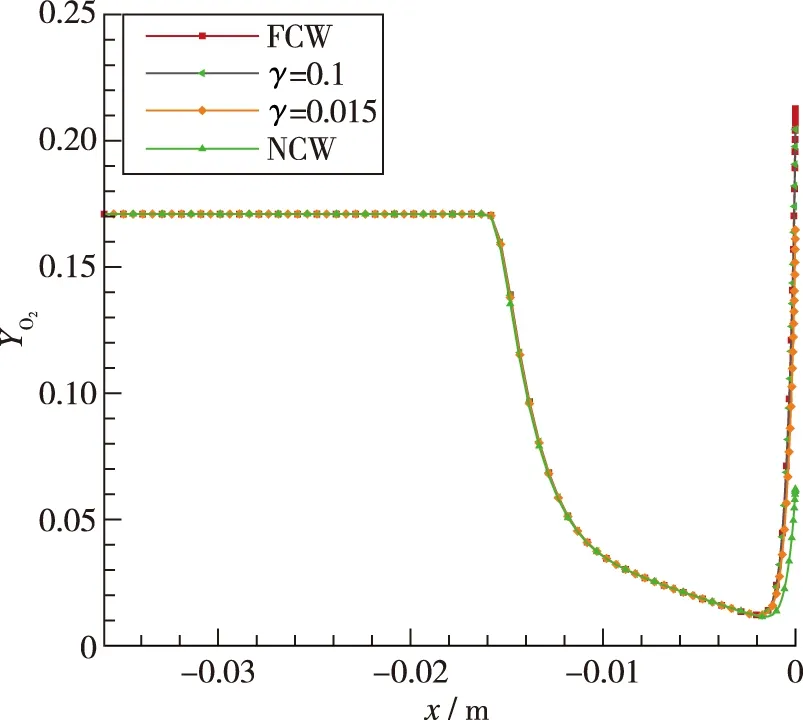
图12 Test-1有限催化氧分子沿驻点线质量分数Fig. 12 Mass fraction distribution of oxygen molecule along the stagnation line at different catalytic conditions in Test-1

3 辐射平衡模型验证

北卡罗莱纳州立大学的 Keenan 等对高超声速球绕流问题进行了数值模拟研究[15], 且在文中考虑了壁面辐射的影响. 本节拟参考该数值模拟的结果, 对本文的辐射平衡模型进行验证. 计算的具体参数如下: 球的半径R=1 m, 壁面的发射率ε=0.9, 海拔高度为H=65 km, 来流速度取 8 km/s.

图13给出了高超声速球头绕流计算所采用的结构网格, 并在激波附近对网格进行了加密, 以便提高对激波的捕捉能力. 图14给出了高超声速球头绕流压强的分布云图, 可以发现来流在经过头部脱体激波后压强迅速增加, 其中在驻点附近由于激波强度最大, 因此压强增加也最为显著.

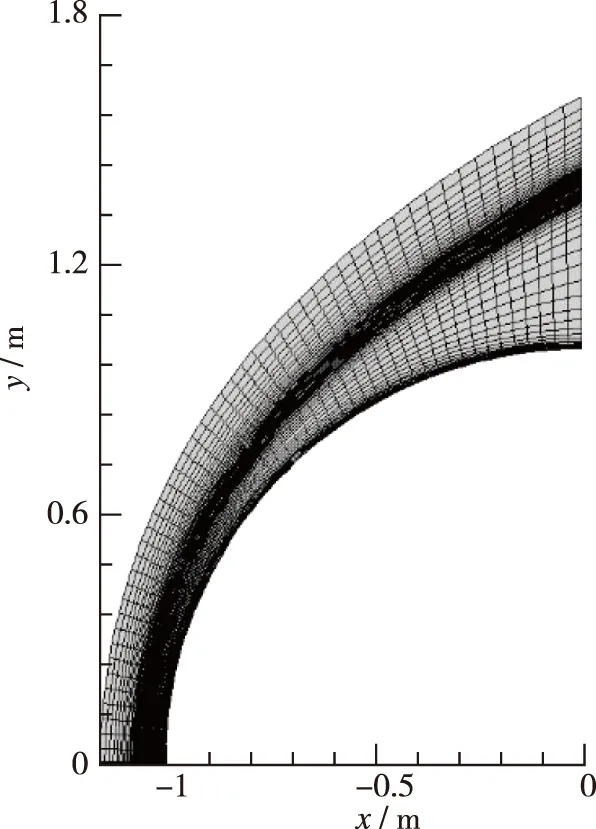
图13 高超声速球绕流网格Fig. 13 Structural grids for the hypersonic spherical body

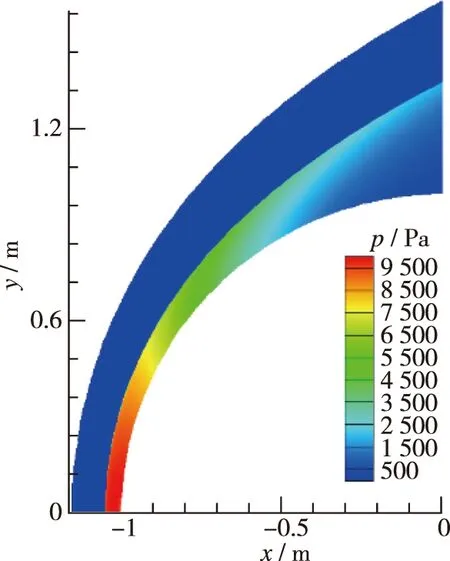
图14 高超声速球绕流压强分布云图Fig. 14 Contour of pressure for the hypersonic spherical body

图15, 16分别给出了球头沿流向壁面上的温度和热流密度分布. 可以看出, 壁面温度与文献结果十分吻合, 热流密度与文献结果在中间部分有一定偏差, 但最大偏差不超过10%. 由此验证了辐射平衡模型在计算壁面温度分布时的正确性, 所以可以将此模型应用于之后的飞行器外形温度分布计算.

图15 温度分布, v=8 km/sFig. 15 Distribution of temperature along the wall， v=8 km/s

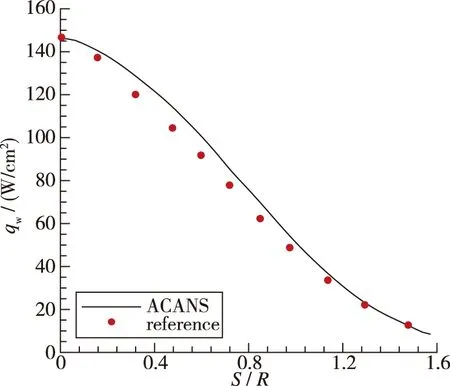
图16 热流密度分布, v=8 km/sFig. 16 Distribution of heat flux along the wall， v=8 km/s

4 辐射平衡壁温有限催化计算

本节借助三维高超声速钝头双锥绕流实验模型[16], 将该模型等比例放大, 放大之后的模型外形参数如下: 钝锥体头部的前缘半径为 0.153 4 m, 前锥体的半锥角为12.84°, 后锥体的半锥角为7°, 两锥的连接处与头部的距离为2.782 m, 全锥总长4.889 6 m. 计算采用的结构网格如图17所示， 其中对双锥头部网格进行了加密处理以便更精确地捕捉头部脱体激波. 计算工况采用STS-2飞行实验来流参数, 如表2所示.

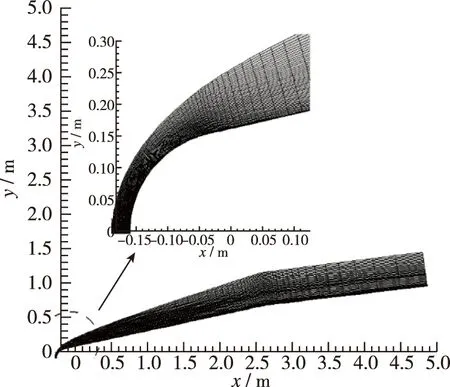
图17 双锥结构网格Fig. 17 Structural grids for bi-cone geometry

表2 双锥计算工况

由于Mach数等于26.3, 静温202.72 K, 总温达到了15 000 K以上, 因此需要考虑电离反应, 采用Gupta 7组分9反应化学反应动力学模型, 壁面催化效应考虑式(4)中的3个反应. CFD计算分别采用完全催化、 有限催化和完全非催化边界条件. 其中， 有限催化模型的氧原子和氮原子催化复合系数采用Scott实验数据拟合结果和Zoby飞行数据修正结果. 考虑到催化复合系数随温度变化的连续性, 因此本节最终采用式(19)的连续形式, 且γNO+取常数.

(19)

图18给出了双锥辐射平衡壁温下有限催化流场温度云图. 图19～21分别给出了完全催化、 有限催化和完全非催化条件下驻点线各组分质量分数分布, 其中NO+和e-由于电离程度较低, 组分质量分数含量极少, 最终这两种组分在图中几乎与x轴重合. 对于氧气、 氮气质量分数, 壁面处完全催化大于有限催化大于完全非催化. NO质量分数, 有限催化大于完全催化大于完全非催化,这与壁面温度及各组分质量分数有关.

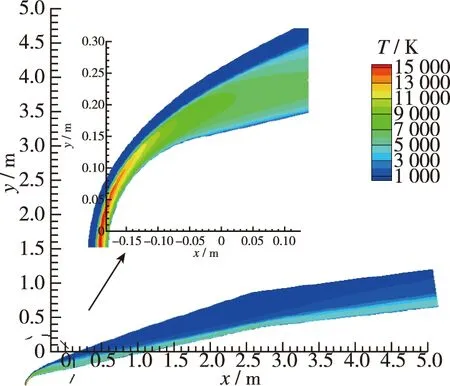
图18 双锥辐射平衡壁温下有限催化温度云图Fig. 18 Contour of temperature at the radiation balanced wall under FRC

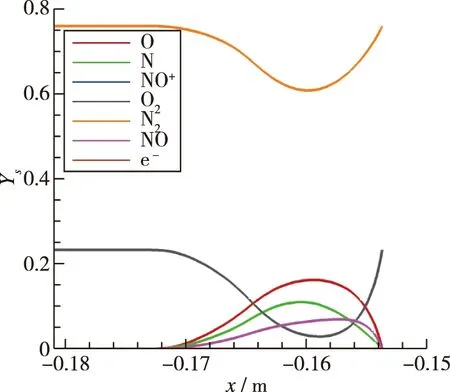
图19 完全催化驻点线组分质量分数分布Fig. 19 Mass fraction distribution of components along the stagnation line under FCW

图20 有限催化驻点线组分质量分数分布Fig. 20 Mass fraction distribution of components along the stagnation line under FRC

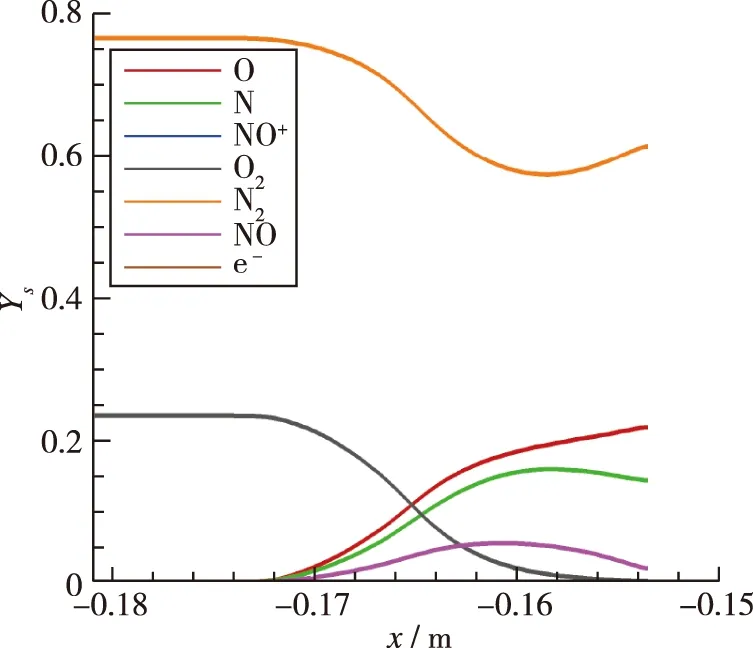
图21 完全非催化驻点线组分质量分数分布Fig. 21 Mass fraction distribution of components along the stagnation line under NCW

图22给出了在辐射平衡边界条件下, 完全催化, 有限催化和完全非催化驻点线温度分布曲线. 表明在高空高Mach情况下, 来流空气稀薄, 激波厚度较厚, 同时壁面催化复合效应也将改变激波位置. 其中完全非催化激波位置离壁面更远, 且驻点温度更低.

图23, 24分别给出了完全催化、 有限催化和完全非催化壁面的温度分布和热流密度分布. 图23表明有限催化下壁面温度的峰值约为2 265 K, 而在大面积区域壁面温度在1 150 K左右, 同时通过式(19)的催化复合系数计算公式求得在驻点附近氧原子的催化复合系数约为0.17, 氮原子的催化复合系数约为0.026, 而在大面积区域, 氧原子的催化复合系数约为0.005 3, 氮原子的催化复合系数约为 0.01. 另一方面对比了图24中3种催化边界的壁面热流密度, 结果表明完全催化的壁面热流峰值比有限催化高约21%, 而完全非催化的壁面热流峰值比有限催化低约29%, 对于大面积的热流分布, 完全催化的壁面热流峰值比有限催化高约10%, 而完全非催化的壁面热流峰值比有限催化低约8.7%.

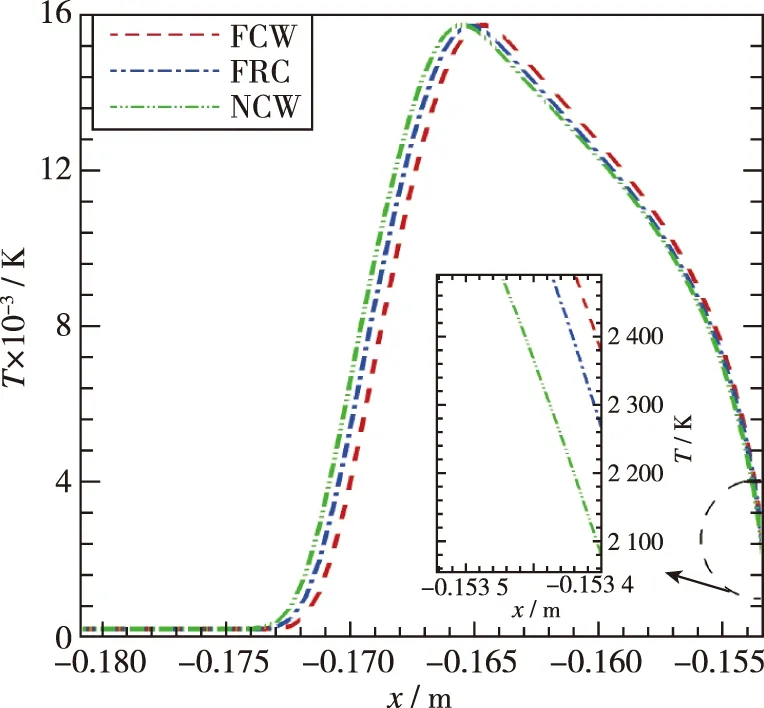
图22 完全催化、 有限催化和非催化驻点线温度对比Fig. 22 Comparison of temperature along the stagnation line between FCW, FRC and NCW

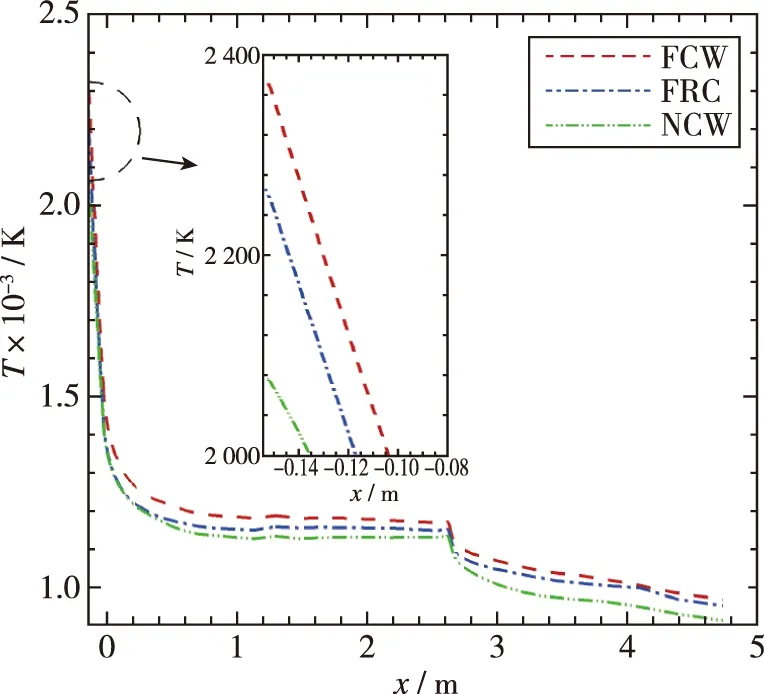
图23 完全催化、 有限催化和非催化壁面温度对比Fig. 23 Comparison of wall temperature between FCW, FRC and NCW

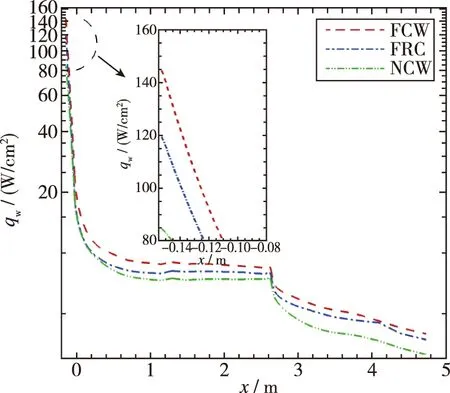
图24 完全催化、 有限催化和非催化壁面热流对比Fig. 24 Comparison of heat flux between FCW, FRC and NCW

图25给出了有限催化壁面总热流、 热传导热流与各组分热流分布. 对比图24， 25中有限催化和完全非催化的热传导热流可以发现, 有限催化条件下壁面的热传导热流显著增加, 这是由于在有限催化和辐射平衡耦合作用下, 使得激波位置相较于完全非催化发生了改变, 且更靠近壁面(如图22所示), 从而使得壁面温度梯度上升, 同时在这种耦合作用下壁面温度也将上升, 进而导致壁面热传导系数上升, 最终使得热传导热流增强. 图26给出了有限催化壁面热传导热流与各组分热流占总热流比值. 结合图25分析可知, 在此来流条件下, 热流密度中热传导引起的热流占主要成分, 质量扩散引起的热流中氧原子扩散引起的热流占主要成分, 且质量扩散引起的热流在头部驻点占比最大, 并随着壁面离驻点的距离增大而下降.

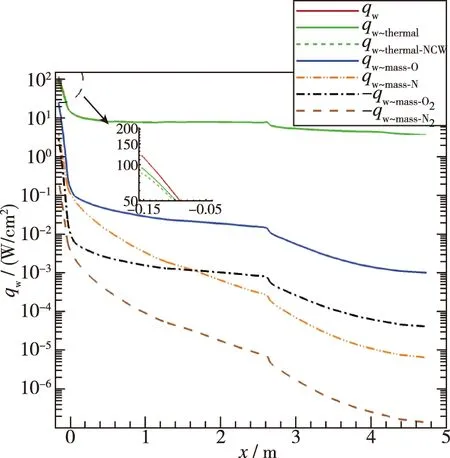
图25 有限催化壁面总热流、 热传导热流与各组分热流对比Fig. 25 Comparison of total heat flux, thermal heat flux and heat flux of each component under FRC

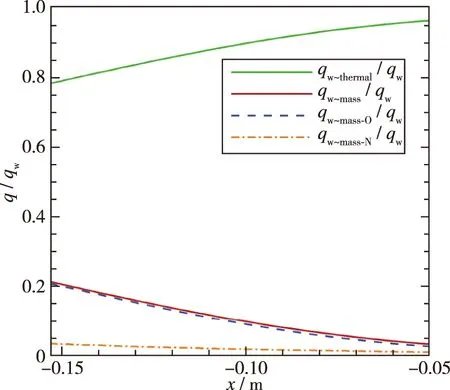
图26 有限催化壁面热传导热流与各组分热流占总热流比值Fig. 26 Ratio of thermal heat flux and heat flux of each component to total heat flux under FRC

5 结论

本文发展了高超声速飞行器辐射平衡壁温下有限催化的数值方法, 基于返回舱外形的风洞实验数据进行了数值模拟结果对比, 并进一步针对典型高超声速飞行器钝双锥研究了辐射平衡壁温下有限催化对气动热环境的影响规律, 主要结论如下:

(1)针对返回舱外形的数值实验结果表明, 完全催化与完全非催化边界条件下壁面热流密度均与风洞实验结果偏差较大, 不能表征真实壁面的催化复合效应, 而采用合适的有限催化模型, 则壁面热流密度与风洞试验结果符合良好, 表明高超声速飞行器壁面的催化复合效应为有限催化.

(2)针对典型高超声速飞行器钝双锥的研究表明, 在辐射平衡温度边界条件下驻点附近氧原子的催化复合系数约为0.17, 氮原子的催化复合系数约为0.026, 大面积区则分别降为0.005 3和0.01. 另一方面, 与完全催化和完全非催化相比, 有限催化对壁面温度和热流分布具有显著影响. 驻点壁面温度方面, 完全催化的壁面温度峰值比有限催化高约5%, 而完全非催化的壁面温度峰值比有限催化低约8%. 驻点热流密度方面, 完全催化的壁面热流峰值比有限催化高约21%, 而完全非催化的壁面热流峰值比有限催化低约29%.

(3)高超声速化学非平衡流场中飞行器壁面的组分复合效应有两个组成部分, 第一是由壁面材料催化直接导致的复合, 第二是由壁面附近低温导致的化学反应速率变化而间接引起的复合. 辐射平衡壁温条件下, 与完全非催化相比, 有限催化效应将间接改变壁面温度梯度及壁面热传导系数, 进而影响热传导热流.

本文建立的高超声速飞行器化学非平衡流场辐射平衡与有限催化边界耦合计算方法具有较大的拓展空间, 未来可结合分子动力学计算得到的壁面催化复合系数, 实现跨尺度的CFD数值模拟.