串列双圆柱时均流场特性分析

邵 山, 陈少松, 魏 恺, 徐一航

(南京理工大学能源与动力工程学院, 江苏南京 210094 )

引 言

在海洋设施建设、 桥梁建设、 核反应堆散热装置等工程建设过程中， 大长细比柱群结构得到了广泛的应用. 圆柱串联排列时, 两圆柱之间的流动相互作用较强[1-5].

Zdravkovich[6]根据间距比L/D(L为两圆柱之间的距离,D为圆柱直径)的不同将流动划分为3种流型: (1)过度流, 即L/D很小, 两个圆柱体作为一个组合的单一绕流结构； (2)再附流, 即L/D中等大小时, 剪切层从上游的圆柱重新连接到下游的圆柱上; (3)脱落流, 即L/D很大时, Karman涡街从上游圆柱脱落. 在再附流和脱落流的边界处存在一个临界的L/D范围, 在这个范围内, 再附流和脱落流都间歇地出现, 从一种流型向另一种流型转换, 称为双稳态流[7]. Sakamoto等[8]和Alam等[9-10]对Re=6.5 × 104的串列圆柱进行了实验, 在脱落流状态下上游圆柱产生的涡引发下游圆柱涡脱落. 他们观察到, 对于给定的下游圆柱, 上游圆柱截面的变化会导致上游圆柱脱落频率的不同. 下游圆柱的涡脱落频率与上游圆柱的涡脱落频率相吻合.

近年来, 由于计算流体力学的迅速发展, 对两串联圆柱绕流的数值研究越来越多. Mittal等[11]采用有限元方法对Re=100和1 000，L/D=2.5和5.5两个串联缸的不可压缩流动进行了二维数值模拟, 结果表明Reynolds数和圆柱间隙比对圆柱后方流动有较大的影响. Papaioannou等[12]进行了二维和三维直接数值模拟, 重点研究了三维效果, 得出了二维模拟对脱落涡频率预测不足而三维模拟可以弥补这一缺陷的结论. Carmo等[13]使用三维直接数值模拟研究了Re=80～500尾流的二次不稳定性, 确定了4种不同的流态, 发现了不同间距比对二次不稳定性有着重要的影响.

目前, 关于串列圆柱的研究主要集中在流动状态的变化以及脱落涡的分析上. 关于串列圆柱后方时均速度的变化相对较少, 缺少相应的实验支撑. 本文通过对Re=12 000, 间距比为L/D=1.167, 2.333, 3.500和4.667的串列后方速度场进行了实验测量, 分析其后方流场变化规律.

1 实验装置与测量技术

1.1 风洞装置

实验在南京理工大学HG-1风洞中进行, 该风洞为开口环流式风洞. 风洞实验段截面积为 700 mm×700 mm, 长1.1 m, 速度范围为(0.1～40)m/s, 湍流度0.97%.

1.2 热线风速仪

采用Dantec StreamLine Pro型热线风速仪对串列双圆柱后方流场进行测量. 热线探头由一根长1.25 mm， 直径5 μm的镀金钨丝焊接于两根不锈钢针尖构成的支架上, 并接入电路中. 热线风速仪的采样频率为5 kHz, 采样时间设定为2 s, 每组实验之前对热线风速仪进行标定.

1.3 移测坐标架控制系统

实验采用的是奈凯移测坐标架系统, 该系统由精密丝杆传动器、 步进电机、 步进电机驱动器、 驱动控制板、 计算机和控制软件组成. 奈凯移测坐标架移测距离为600 mm×600 mm×600 mm, 移测精度为 0.02 mm, 通过软件控制该坐标架可以实现定步长运动.

1.4 实验装置示意图

如图1所示, 以圆柱轴线为中心向上、 下共选取41个测量点, 每两个测量点之间的距离为2.5 mm. 为了保证测量的准确性, 在每一组实验之前对热线风速仪进行标定. 将热线探针固定在移测坐标架的支臂上, 通过软件控制移测坐标架的移动, 从而对串列双圆柱的后方流场进行准确的测量. 热线风速仪分别对串列圆柱后方4处截面的速度进行测量, 每个截面到后方圆柱轴心的距离分别为1D， 2D， 4D和10D, 圆柱直径D=30 mm. 图2为实验装置示意图. 热线探针在圆柱后面的分离区域内测量速度和湍流度可能存在一些误差, 但是在自由剪切层外其测量结果是准确的. 圆柱后方分离区域自由剪切层由外到内速度会经历突变, 热线风速仪对这一位置的测量是准确的.

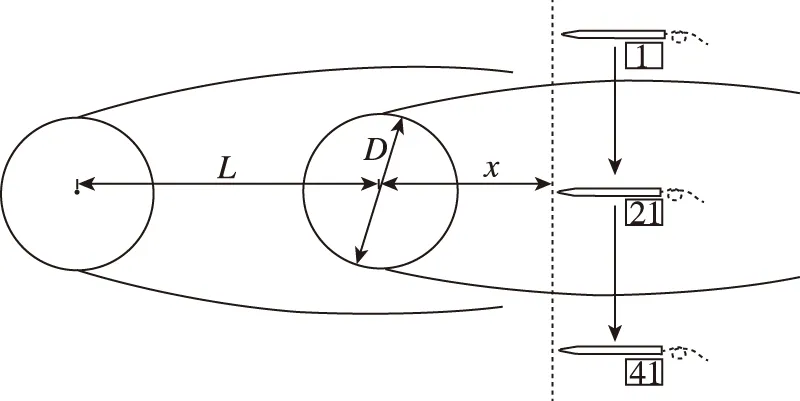
图1 串列圆柱测量示意图Fig. 1 Schematic diagram of measuring two tandem cylinders

图2 实验装置示意图Fig. 2 Experimental equipment

2 实验结果分析

2.1 时均速度分布

图3给出了Re=12 000， 间距比L/D=1.167, 2.333, 3.500和4.667的串列圆柱后方速度场分布示意图, 图中速度突然发生变化的位置即为自由剪切层的位置. 与单圆柱相比, 当串列圆柱间距比较小时(L/D=1.167), 后方圆柱后面的自由剪切层比较明显. 与单圆柱不同, 后方圆柱的自由剪切层明显向内偏移, 这是由于两个圆柱距离较近, 两个圆柱体作为一个组合形成了单一的绕流体所产出的结果. 随着x/D的增加, 圆柱后方的速度逐渐趋于平稳. 尤其是在x/D=4， 10处, 其最大速度衰减量Δu要比单圆柱小, 这说明间距比较小的串列圆柱对尾流有较好的整流作用.

随着间距比的变大, 后方圆柱的自由剪切层变得越来越模糊, 这是由于前方圆柱的尾流对后方圆柱产生了干扰. 在中等间距比时(L/D=2.333, 3.500), 后方圆柱后速度分布在x/D=1, 2处有较大的差异, 随着x/D的增加, 其速度分布与单圆柱较为相似. 但是对于间距比(L/D=4.667)较大的串列圆柱, 其在x/D=2, 4和10处的最大速度减小量Δu要比单圆柱大, 这说明间距比大的串列圆柱对后方流场的扰动较强.

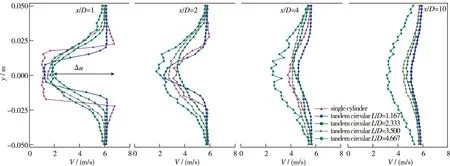
图3 Re=12 000时串列双圆柱后方4个剖面无量纲时均速度分布Fig. 3 Dimensionless mean velocity distribution of 4 profiles behind the tandem double cylinders at Re=12 000

2.2 时均湍流度分布

图4为Re=12 000, 间距比L/D=1.167, 2.333, 3.500和4.667的串列圆柱后方湍流度分布示意图, 采用如图5所示的二维探针进行测量. 与速度分布相似, 在小间距比时串列圆柱对尾流湍流度有较好的整流作用. 在中等间距比时, 尾流湍流度分布与单圆柱较为相似. 在较大间距比时串列圆柱对尾流湍流度有较大的影响.

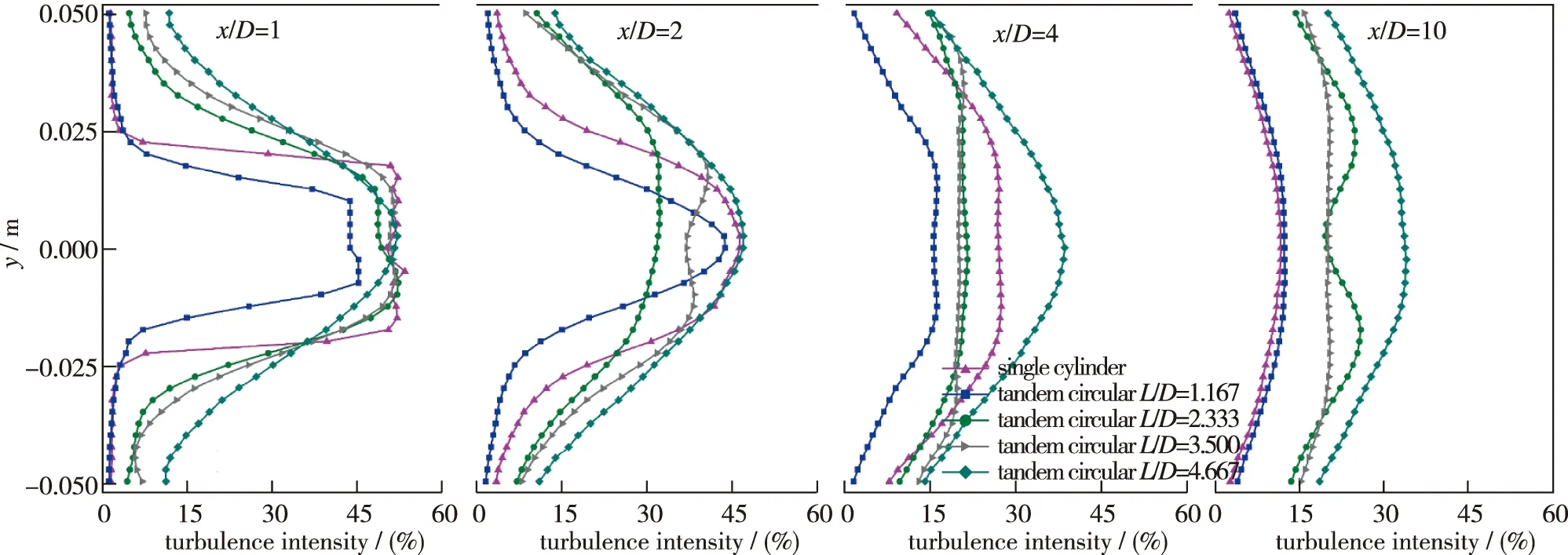
图4 Re=12 000时串列双圆柱后方4个剖面无量纲时均湍流度分布Fig. 4 Dimensionless mean turbulivity distribution of 4 profiles behind the tandem double cylinders at Re=12 000

图5 二维探针示意图Fig. 5 Two-dimensional probe diagram

3 流函数理论

两个间距比较近(L/D=1.167)的圆柱体作为一个组合的单一绕流结构, 可以采用流函数理论分析其后方自由剪切层和速度分布. 将两个绕圆柱的有环量流动与两个有夹角θ的点涡列进行叠加, 得到了如图6所示的流动分布. 圆柱后方流场中任一点处速度为

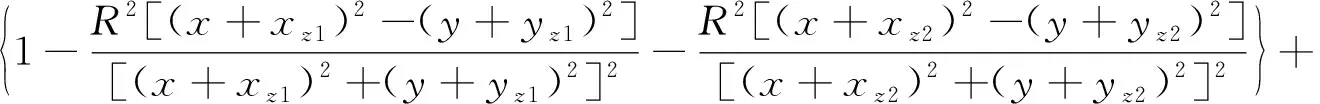
(1)

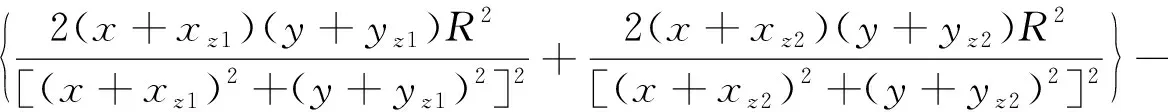
(2)

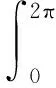
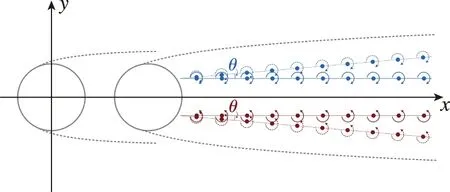
图6 串列圆柱时均涡分布模型Fig. 6 Time-averaged vortex distribution model for two tandem circular cylinders

圆柱后方Karman涡街脱落后并不是沿着x方向顺来流向后发展, 而是和x轴呈一定的夹角(如图6中所示). 夹角θ的大小和涡的位置对圆柱后方的自由剪切层和速度分布有着重要的影响.

图7和8分别为单、 双圆柱后方流场x/D=1处理论模型与实验值对比图, 流函数理论模型与实验值吻合较好, 可以很好地预测自由剪切层的位置(即速度突然下降位置). 此时的单圆柱θ为12.5°, 涡核的位置为距离x轴0.013 5 m处； 而串列双圆柱(L/D=1.167)的θ为5°, 涡核的位置为距离x轴0.01 m处. 这说明串列双圆柱由于两个圆柱的相互干扰, 使得圆柱后方涡相互靠近, 并且后方涡向外倾斜的角度也减小, 自由剪切层向内侧偏移.

图7 单圆柱后方流场x/D=1处理论模型与实验值对比图Fig. 7 Comparison of flow field behind single circular cylinder at x/D=1

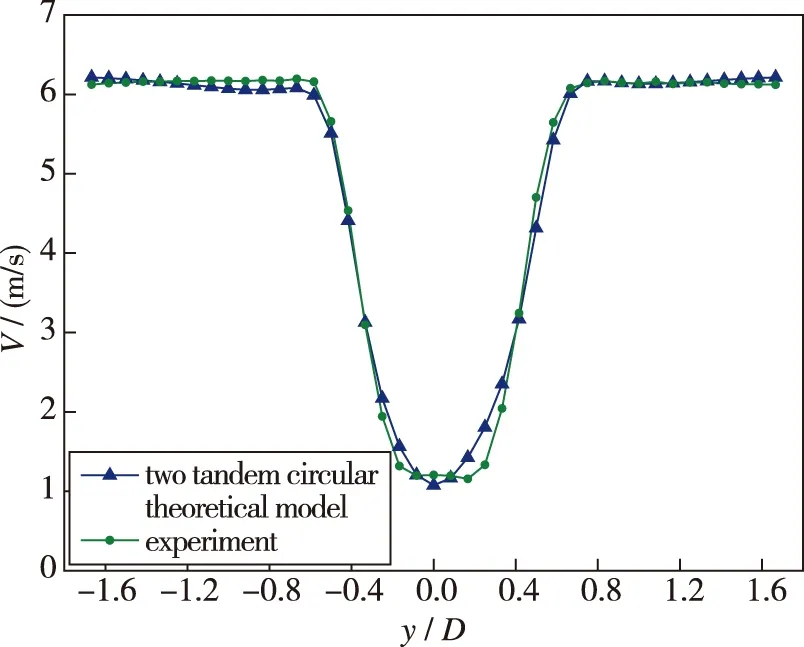
图8 双圆柱(L/D=1.167)后方流场x/D=1处理论模型与实验值对比图Fig. 8 Comparison of flow field behind two tandem circular cylinders(L/D=1.167) at x/D=1

4 结论

本文采用热线风速仪对Reynold数为12 000的串列双圆柱后方流场进行了测量, 并通过流函数理论模型对小间距比串列双圆柱后方流场特性进行了分析, 得出如下结论:

(1)与单圆柱相比, 当串列双圆柱间距比较小时, 后方圆柱的自由剪切层明显向内偏移. 随着间距比的变大, 由于前方圆柱的尾流对后方圆柱的干扰, 后方圆柱的自由剪切层变得越来越模糊. 对于间距比较大的串列双圆柱, 其对后方流场的扰动较强, 致使后方流场湍流强度和最大速度衰减量较大.

(2)通过流函数理论模型分析发现, 在小间距比条件下, 串列双圆柱由于两个圆柱的相互干扰, 使得圆柱后方涡相互靠近, 并且后方涡向外倾斜的角度也减小, 自由剪切层向内侧偏移.