空间引力波探测正三角形编队动力学机理与控制方法

刘培栋 党朝辉

1．西北工业大学航天学院航天飞行动力学技术重点实验室陕西西安710072

引力波是时空曲率受黑洞并合等剧烈过程影响产生的波动[1−9].引力波探测为揭示宇宙演化、基础物理学规律等提供了新的方法和手段.然而,受制于地面干扰及干涉臂长限制,地面探测器仅能探测到约10 Hz 以上的高频引力波,对于其他在科学上有重大意义的中低频引力波则无能为力.空间引力波探测利用卫星编队超大基线(数十万∼数百万公里)的优势,可有效实现毫赫兹频段引力波探测,是对引力波探测技术的重大突破[3−5],已经成为当前各航天大国争相发展的焦点.

欧洲空间局(European Space Agency,ESA)与美国航空航天局(National Aeronautics and Space Administration,NASA)于1993年最早提出了空间引力波探测计划LISA 项目[6−7].随后,日本、欧洲等也先后提出了类似的计划,如DECIGO(2001)、BBO(2004)、ALIA(2005)等.我国从2008年开始探讨空间引力波探测的可行性[1−3],先后开展了概念与方案设计、关键科学载荷研制等,并于2014年和2016年提出“天琴计划”和“太极计划”[1,2].2020年、2021年,科技部连续发布国家重点研发计划“引力波探测”重点专项指南,布局未来十年内的引力波探测关键技术攻关,并计划在2035年前实现空间引力波探测在轨试验.

空间引力波探测可推动关乎我国重大战略利益的技术发展[4−5].通过开展毫赫兹频段引力波探测,可以全面推动高精度空间惯性基准、星间激光干涉测量、高精度卫星编队、超静超稳卫星平台技术等,带动一系列对国民经济和国家战略需求有重要价值的关键技术的发展,对于建立高精度全球时空坐标体系、全球重力场测量、导航与深空探测,以及前沿空间科学实验等都具有重要的意义.

空间引力波探测的基本原理是通过三颗航天器形成空间正三角形编队,以迈克尔逊激光干涉方式,测量航天器间由引力波引起的距离变化[1−2].其特殊的测量原理要求编队构形为完全等边三角形,三边边长相等、内角均为60◦[1−9].空间引力波探测的基本要求是确保空间正三角形编队的动力学稳定,实现引力波探测信号不被卫星自身运动及环境噪声淹没[10].

然而,受中心天体非球形引力摄动、三体引力摄动等的影响,空间正三角形编队的构形稳定性极易遭到破坏.为了保证探测器相对测距精度,按照引力波探测科学要求,编队构形稳定性必须控制在1%以内[1−3].而且构形指标变化范围越小,对硬件要求就越低,越容易在工程上实现[9].由于编队动力学的非线性,构形稳定条件的数值搜索需要耗费大量计算时间,在无动力学机理引导的情况下,很难给出精度高、过程稳定,同时又能反映系统真实物理性质的数值解[1].为此,需要重点突破空间正三角形编队的动力学形成机制及摄动发散机理.

在动力学机理阐明的基础上,高效的空间正三角形编队构形控制是引力波探测开展的前提[11].构形控制包括构形初始化控制和构形重构控制.其中,前者解决编队构建问题,后者解决编队构形保持与调整问题.未来的编队控制技术会朝着自主化、智能化、安全化的方向发展[12],甚至可能会发展基于数据链组网架构的动态协同策略[13].然而,有别于已经广泛研究的近距离编队和星座系统,空间引力波探测编队具有尺度超大(数十万∼百万公里量级)、推力极小(微牛级别及有限机动能力)、精度极高(≤1%)、时间极长(数月∼数年)的特点,这给经典编队控制理论提出了前所未有的挑战.

遗憾的是:面对如此重大的国家战略科技需求,空间正三角形编队的动力学与控制研究,目前大多局限于特定的工程任务和可行性分析上,缺乏系统深入的动力学机理与控制方法研究.作为航天器编队动力学与控制领域的学者,如何从编队动力学角度发现和分析面向引力波探测的空间正三角形编队运行过程的科学问题,并通过航天器轨道动力学学科与控制学科所特有的手段有效地予以解决,是摆在我们面前不可回避的问题,我们应作出最积极的反应.

因此,亟需建立一套完整的空间正三角形编队动力学与控制理论,系统揭示引力场轨道动力学约束下空间正三角形编队构形的形成机理,深入阐明复杂摄动影响下,超大尺度编队构形演化规律及长期稳定条件,完整创建多约束条件下的空间正三角形编队构形初始化及重构控制方法,为我国“天琴”、“太极”等空间引力波探测任务的编队飞行控制设计与优化奠定理论基础.

1 空间正三角形编队的动力学机理

空间正三角形编队的动力学机理包括正三角形编队构形的形成机制与摄动发散机理.

1.1 空间正三角形编队的形成机制

任意3 颗卫星均可形成三角形编队,但若要求在轨道运动中始终保持各边相等则非常困难;这需要极为特殊的动力学条件.由于空间引力波探测的需要,研究人员提出3 种有效的空间正三角形编队机制[1−3]:1)共轨星座方式;2)相对绕飞方式;3)三角平动点方式.编队尺度从1 000 km 到8.6 AU,如图1所示.

图1 空间引力波探测的三类空间正三角形编队Fig.1 Three kinds of triangular formations for space-based gravitational-wave observatory

共轨星座方式形成正三角形编队的基本原理为:3 颗航天器相隔120◦均匀分布在同一条圆轨道上围绕共同的中心引力体(地球或太阳)运动,利用圆轨道运动速度恒定的规律,形成稳定的等边三角形.从轨道动力学机理上分类,这种正三角形构形本质上是一种卫星星座.典型代表为“天琴计划”[1](以地球为中心,高度10 万公里,边长约17 万公里)、OMEGA[14](高度60 万公里,边长约100 万公里)、gLISA/GEOGRAWI[15](地球静止轨道,边长7.3万公里)、GADFLI[16](与前同)、B-DECIGO[17].

相对绕飞方式形成正三角形编队的基本原理为:3 颗航天器相隔120◦均匀分布在圆参考轨道附近的一个空间相对绕飞圆上,绕飞圆的平面与轨道平面(例如黄道面)夹角为±60◦,编队会随着绕飞圆而旋转,周期与参考轨道周期一致(当为地球公转轨道时,周期正好为1 a).典型代表为“太极计划”[6]、LISA[18]、eLISA[1,5]、ALIA[3]、DECIGO[17],均沿地球公转轨道运动,其边长分别为300 万公里、500 万公里(后又改为250 万公里)、100 万公里及1 000 km.

三角平动点方式形成正三角形编队的基本原理为:3 个航天器位于平面圆型限制性三体的L3、L4、L5 平动点附近构成正三角形.典型代表为LAGRANGE[19]、ASTROD-GW[8−9]、ASTRODEM[3]、Super-ASTROD[3]等飞行计划.其中,LAGRANGE 位于地月系统,边长67 万公里;ASTRODGW 位于日地系统,边长2.6 亿公里.尽管已提出了上述3 种正三角形编队形成机制,但是否还具有其他可能的机制?这是现有文献中尚未研究的.

在上述原理的指导下,如何具体设计空间正三角形编队构形? 对于类LISA 编队,Folkner等[20]、Nayak 等[21]、李广宇等[22]建立了一种基于轨道几何关系的空间正三角形编队构形设计方法,首先确定其中一颗卫星的轨道,然后通过绕垂直黄道面方向旋转±120◦,得到另外两颗卫星的轨道.而Dhurandhar 等[23]、Marchi 等[24]则建议采用相对轨道动力学的Clohessy-Wiltshire(CW)方程构造出相对绕飞圆,然后通过相位均匀分配实现正三角形构建.杨弛航等[25]指出,由于CW 方程仅有一阶精度,因此,设计后的构形需要通过进一步优化才能达到要求.对于类“天琴”编队,张雪峰等[26]、万小波等[27]、叶伯兵等[28−29]、檀庄斌等[30]在系列论文中给出了初步的设计方法,建立了轨道面和轨道半径的选取方法,分析了地月系引力场干扰,研究了地影规避方法,并通过数值优化搜索改进构形设计.对于类ASTROD-GW 编队,倪维斗等[3,9]、门金瑞等[8]以日地平动点L3∼L5 点附近的三条绕日圆轨道作为初值,提出了详细的正三角形编队设计方法.

1.2 空间正三角形编队的摄动演化机理

空间正三角形编队在复杂摄动下的演化规律是重要的研究问题,对引力波探测方案的优化具有重要意义.

LISA 研究团队对相对绕飞方式的空间正三角形编队演化规律进行了深入研究[20−25,31−34].Cornish等[33]通过精确轨道积分发现基于CW 方程一阶线性解构造的正三角形编队在演化过程中存在“呼吸现象”:三角形内角(也称作呼吸角)具有一个缓慢的波动,并由此带来三角形边长(也称作臂长)的屈伸变化.由于呼吸现象导致的臂长峰值变化量会达到115 000 km(等效误差为2.3%),明显超出了引力波探测要求的≤1%误差.为解决上述问题,Nayak等[21]构造了考虑非线性引力的二阶CW 方程解析解,并由此推导得到了编队倾角与臂长峰值变化量之间的解析关系.Nayak 等[21]发现,若将编队倾角标称值(±60◦)进行小范围修正(0.47◦∼0.63◦),可将三年臂长变化量降低到60 000 km(等效误差为1.2%).李广宇等[22]基于不同方法也得到了类似的修正结果.Dhurandhar 等[34]在Nayak 等[21]的基础上进一步构造了考虑三体引力摄动的二阶CW 方程解析解,将臂长的3年变化量降低到了48 000 km(等效误差为0.96%).Pucacco 等[31]在以上二阶CW 方程模型上进一步考虑了太阳相对论进动(relativistic precession)和太阳引力四极矩的影响.易照华等[35]针对LISA 三角形编队问题,建立了一种考虑地球引力摄动的共轨限制性三体(co-orbital restricted problem)动力学模型,并通过摄动法得到了编队质心滞后角及其矢径的近似解析解.基于上述解析结果,李广宇等[22]进一步研究了初始质心滞后角与编队质心漂移的规律,发现标称20◦的滞后角若能修正为22◦,则编队具有最小的漂移.同时,李广宇等[22]还以上述解析解为基础,通过数值优化搜索得到了10年任务期里最小漂移构形(等效误差为1.26%∼1.82%).夏炎等[36−37]进一步改进了上述优化方法,通过采用混合反应禁忌搜索算法,使臂长变化量减小到49 960 km(等效误差为0.99%).

“天琴计划”的研究团队对共轨星座方式下的空间正三角形编队演化规律进行了详细研究[26].张雪峰等[26]、叶伯兵等[28]指出,为实现空间引力波探测,“天琴”的构形稳定性在5年任务期里需满足:臂长变化量≤0.5%,相对速度≤10 m/s,呼吸角≤0.2◦.万小波等[27]发现平均半长轴不同时会对构形发散起到主导作用,因此,通过平均轨道根数优化,将“天琴” 构形稳定性改进到:臂长变化小于1 500 km(等效误差为0.88%).张雪峰等[26]发现,只有同时匹配平均半长轴、倾角和升交点赤经,才能更好维持构形稳定性;这一发现与J2 不变相对轨道[38−39]的研究机理一致.叶伯兵等[28]发现在“天琴”的标称轨道高度上,月球引力摄动影响最大,其次为太阳引力和地球J2 摄动,且编队指向在上述摄动作用下存在大约2.5◦的长期漂移.檀庄斌等[30]发现,月球引力对“天琴”的编队构形影响主要发生在几个共振轨道高度上,当避开共振高度后,构形具有较好稳定性(误差可降低到0.3%);当编队位于黄道面内时,月球引力影响较大,而在90◦和140◦倾角时影响极小[26].叶伯兵等[29]研究了月食和地球阴影规避问题,研究表明若将轨道高度提升约900 m、形成与月球1:8 的共振,效果明显.“天琴”团队同时还采用数值优化进一步改进编队构形的稳定性,现有技术已可实现“3 +3”个月观测期内编队臂长变化量≤0.1%,相对速度≤4 m/s,呼吸角变化≤0.1◦[26,28].

由于L3 点为弱不稳定点且不稳定时间尺度大(55.6 yr),L4、L5 均为稳定点,因此,基于平动点的空间正三角形编队总体上较为稳定[8].即便如此,通过调节轨道平均周期和偏心率,可以进一步改进ASTROD-GW 的稳定性[40−41].

综上可知,空间正三角形编队的动力学机理已取得一定研究成果,但也存在一些局限性.一是从工程应用角度提出了3 种不同的正三角形编队形成机制,但是否还存在其他机制不清楚;二是现有构形设计方法能够初步达到引力波探测的稳定性要求,但稳定性指标能否进一步提升以及其极限是什么尚不清楚;三是现有构形优化方法只能针对具体轨道或特定引力波探测任务提供数值优化结果,而对各类不同任务、不同尺度以及不同机制下的正三角形编队的一般摄动发散机理及内在稳定性规律未作充分阐明.

1.3 研究建议与思路

结合天体力学规律,尤其是日地月系统的时间尺度特征规律,对现有3 种机制下形成的正三角形编队对应的编队尺度范围、探测频段范围、探测方向范围进行系统梳理和比较,并在此基础上对各类机制对应的最佳探测对象进行编目分析,形成完备的空间正三角形编队构形图谱.

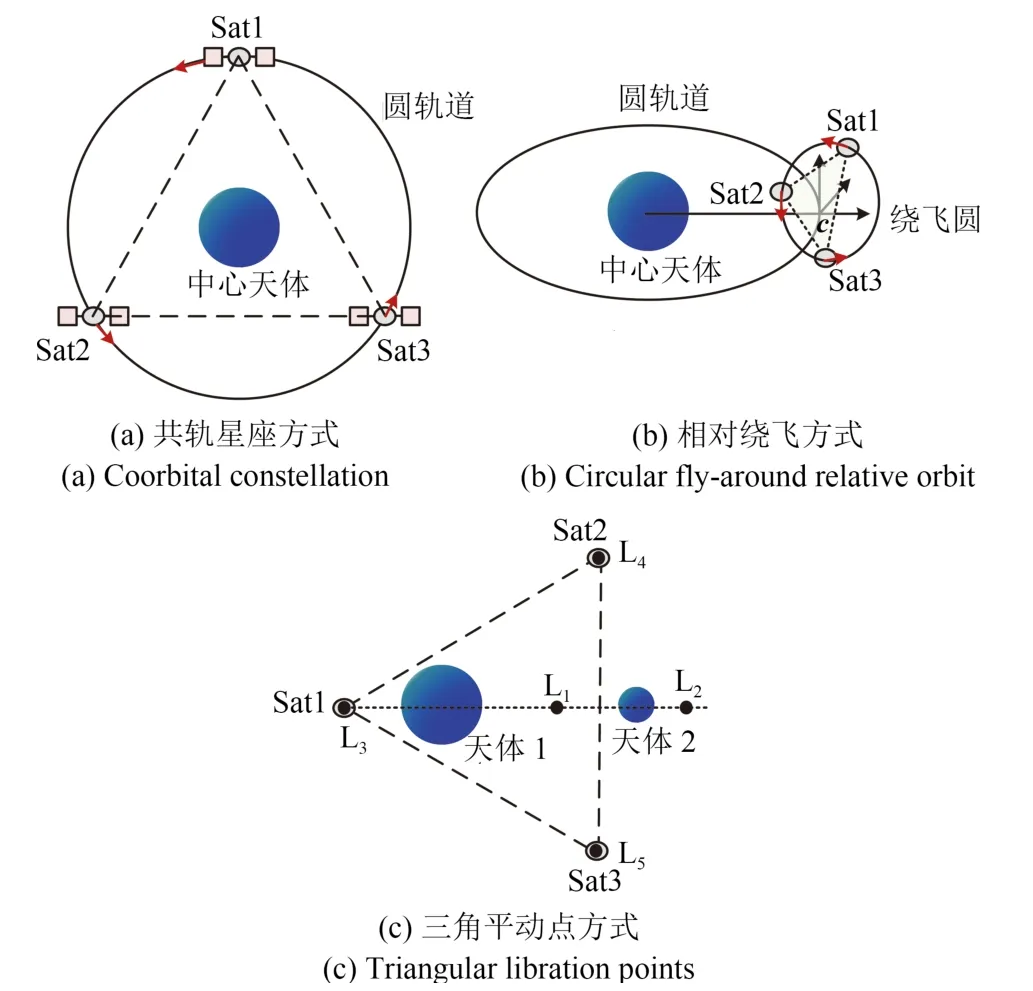
图2 3 种不同的空间正三角形编队构形生成方式Fig.2 Three different generation methods of space-based triangular formation

然后,重点对基于绕飞方式的正三角形编队形成机制进行优化改进.经典CW 方程是一组描述相对轨道运动的线性定常系统,具有显式解析解;通过满足y方向的速度条件,可进一步构造出周期解.在所有周期解中,通过施加约束条件x2+y2+z2=d2,可找到一组称为空间圆的绕飞构形初始条件,其规定了绕飞圆半径和初始相位角到初始相对状态的映射关系:当3颗卫星在绕飞圆上分布时,通过满足相位角关系:可实现三星在任意时刻构成空间正三角形编队.

但CW 方程仅具有一阶精度,由其解析解构造的正三角形编队构形,在真实非线性引力场及摄动干扰下会迅速发散.为解决该问题,可通过非线性摄动技术、能量匹配原理、摄动平均化方法的综合运用,首先得到相对运动高阶周期解并设计出空间正三角形基准构形;然后以此解为基础,以其修正量为优化变量,采用分层优化和全局数值搜索实现稳定构形的精确构造.具体原理如下:

1)非线性摄动技术(perturbation technique)是处理弱非线性尤其是小扰动动力学问题的经典数学方法,可对形如的动力学积分问题有效解决,其中ε 为弱非线性或小扰动(ε ≪1)对应的参数.其中,对应CW 方程的线性动力学,N(XXX,ε)可根据研究需要对应二体引力差、主星轨道偏心率、非球形引力摄动、三体引力摄动等(其中,弱非线性参数ε 根据应用场景分别对应偏心率e、非球形摄动系数J2或三体质量比µ等).具体计算原理为:首先求解线性动力学部分得到一阶近似解XXX(1);然后代入二阶非线性动力学得到二阶近似解XXX(2);以此类推,直到得到各阶修正量XXX(N);最后,获得高阶解析解XXX=XXX(1)+εXXX(2)+···.

2)上述摄动法得到的高阶解析解,能够在短时间范围内对真实解进行严格逼近,但在长时间范围后因截断误差会发散.考虑到二体轨道运动的周期性,因而可通过能量匹配原理(energy matching principle),将各星初始相对状态进行修正,从而使多星之间的相对运动严格满足周期性,确保相对运动有界.但在复杂摄动情形下,单星绝对轨道可能不具有周期性,因此,无法通过能量匹配进行精确周期调节;此时可通过轨道动力学理论中的摄动平均化方法(averaging theory)分离出长期项,并通过匹配长期变化率最小化构形发散.

3)以上解析方法能够消除大部分构形发散,但相对运动中残余的短周期涨落,仍会导致正三角形臂长、呼吸角等的波动,影响引力波探测的精度.为此,可在高阶解析解XXXi0的基础上,构造初始相对状态的修正量∆XXXi0,采用数值优化方法使残余波动振幅最小化.借鉴LISA 任务中采用的优化模型,但将优化变量由轨道根数改为更容易利用高阶解析解的直角坐标状态,如式(1)所示:

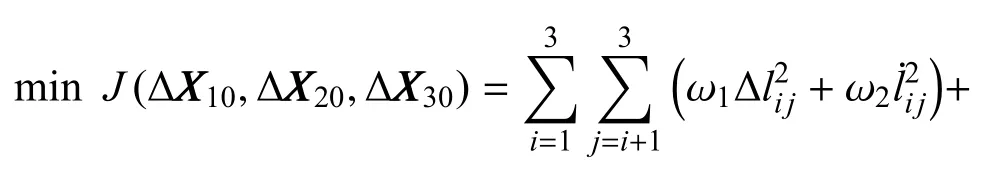
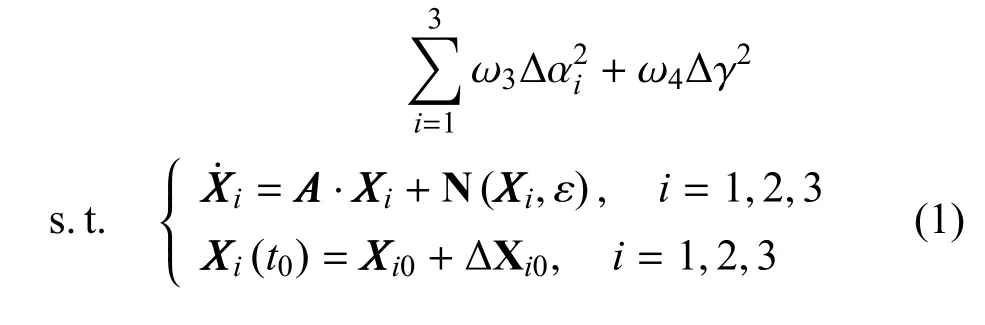
其中:XXXi为第i个卫星的相对状态矢量,XXXi0表示通过解析方法得到的初始相对状态高阶解,∆XXXi0为拟优化搜索的初始相对状态修正值.优化目标J定义为多个构形参数变化量的加权函数,加权系数为ωj(j=1,··· ,4);构形参数包括:li j表示卫星i和j之间的臂长,表示臂长变化率,αi表示卫星i对应的呼吸角,γ 为编队中心滞后角.

上述优化问题直接求解较为困难,主要原因是:一是优化变量较多,含3 个卫星共18 个初始相对位置和相对速度修正量;二是优化过程涉及动力学积分,且动力学方程因非线性和摄动干扰的引入较为复杂,长时间数值积分(例如数年)需要极长的计算时间;三是优化目标存在数量众多的局部极小值,容易陷入局部最优而无法找到最优解.为解决上述3个困难,采取的思路如下:

1)针对优化变量较多的问题,基于轨道动力学内在规律进行降维处理.首先将相对位置和相对速度进行分层优化,其中,相对位置修正量作为外层优化变量,相对速度修正量作为内层优化变量;其次,根据编队距离内在约束,将相对位置变化限定在球壳范围内,从而减少一个自由度;最后,根据能量匹配原理或摄动项长期变化率匹配关系,将相对速度修正量作出约束,从而再减少一个自由度.由此可将原有的18 维(6×3)优化问题降低为12 维(4×3),且因为分层优化而每次仅有6 个变量进行搜索,从而大大提高优化效率.

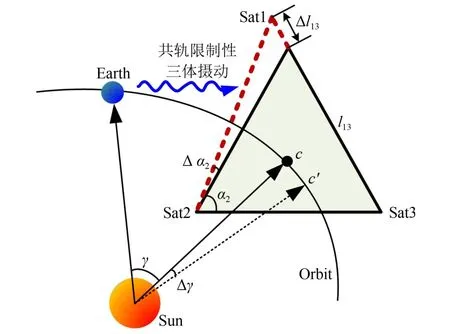
图3 空间正三角形编队的构形参数及其变化量示意图Fig.3 The configuratio parameters and the variation diagram of space-based triangular formation

2)针对动力学积分耗时大的问题,构造轨道运动积分延拓算法进行处理.如图4所示,我们提出一种基于离散解析数据库及差分计算的保精度轨道积分延拓算法(算法1:轨道积分延拓算法).其中,离散解析数据库的构建方式为:a)将初始状态附近的位置速度空间进行网格划分,同时对时间轴进行离散化;b)对网格空间的每个离散点进行精确积分,得到未来离散时刻上的精确状态;c)将所有“时间状态”对保存为数据库;d)当需要离散时刻之间的状态时,通过高阶解析解进行递推求解;e)当需要非离散点的积分结果时,则通过附近离散点积分结果构造状态转移矩阵,进而插值得到相应结果.

图4 保精度轨道积分延拓算法原理Fig.4 Principle of orbit integral continuation algorithm with guaranteed accuracy

3)针对优化目标存在大量局部极小值的问题,通过构造分层全局优化算法加以解决.在LISA 编队构形优化中,现有研究使用了混合反应禁忌搜索算法,基本思想是将适用于局部函数优化问题的仿射筛选算法,和适用于全局组合优化的禁忌搜索算法结合使用.计算实践表明,该算法具有较高的搜索效率和稳定性.因此,可借鉴该方法的基本原理,并通过结合所提出的高阶摄动解析解作为优化初值、轨道积分延拓算法,用于动力学积分计算、分层优化提高优化效率,最终使全局最优性得到大幅改进(算法2:分层禁忌搜索算法).

值得说明的是,基于绕飞式的空间正三角形编队形成问题,本质上等价于:引力场轨道运动中是否存在完美圆形相对运动(perfect circular relative motion)? 也就是说:在二体引力场、考虑J2摄动的引力场、或考虑三体摄动的引力场中,是否存在精确的空间绕飞圆相对运动?如果存在,则用于引力波探测的编队可以无限优化,即得到构形发散极小的正三角形编队;如果不存在,那么完美圆可以接近的理论极限是多少? 在二体非线性引力情况下,截至二阶精度为止,LISA 研究团队通过数值方法得到的极限结果与完美圆的偏差为0.96%;而通过二阶分析解引导数值搜索,可将相对圆构形偏差减小到0.021%(见图5).根据相对圆构形的极值点分布规律(见图6),现有结果似乎支持完美圆形相对运动不存在的结论.但无论上述问题最终结果如何,这都将既是一个有趣的理论猜想,也是一个重要的应用问题.

图5 二体非线性引力下的空间正三角形构形优化结果Fig.5 Optimization results of spatial equilateral triangle configuratio under two-body nonlinear gravity fiel

图6 二体非线性引力下相对圆运动多极值点分布规律Fig.6 Distribution law of multi-extremum points of circular relative motion under two-body nonlinear gravity fiel

未来将根据实际难度和可行性,拓展探索空间正三角形编队的其他可能形成机制—例如平动点附近的周期相对运动或太阳帆编队.如果存在,则空间引力波探测的编队设计和工程实施方案会更灵活、更丰富.

2 空间正三角形编队构形控制方法

动力学机理是解决“如何设计编队”的问题,而构形控制是解决“如何使编队运行”的问题,两者之间具有紧密的耦合关系[39].

2.1 空间正三角形编队的构形初始化控制

编队构形初始化是指构成编队的多个航天器从运载平台(一般为火箭上面级或母星平台)上分离采用脉冲或连续控制进入目标构形各自位置的过程.

Sweetster 等[42]研究了LISA 编队构形的初始化控制问题.其初始化控制的起点是以太阳为中心比地球公转轨道略高的圆形停泊轨道;由于停泊轨道周期比地球公转轨道周期略长几个星期,因此,在发射入轨一年后,3 个卫星将随着运载器到达距离地球后方20◦的位置.以此时的状态为起点,Sweetster等[42]计算得到了三星通过9 个月的转移各自到达目标构形位置的三脉冲速度增量需求(也即燃耗需求).结果表明900 m/s∼1 096 m/s 的速度增量即可完成构形初始化.由于脉冲初始化控制存在一定误差,Sweetster 等[42]建议初始化控制完成后需要一个构形校准控制,以实现正三角形构形对动力学初始条件的严格要求.但该文没有介绍脉冲控制和构形校准控制的具体算法.

夏炎等[36−37]同样研究了LISA 编队的构形初始化问题.与Sweetster 等[42]的方案略微不同,夏炎等[36−37]考虑从期望编队构形的中心开始分离3 个航天器,并进而通过各航天器的脉冲机动控制进入各自的构形位置.夏炎等[36−37]采用二体问题的Lambert 算法求解分离(起始)和制动(末端)所需要的两脉冲速度增量.研究结果表明,当转移过程的时间大于80 d 后,所需的两脉冲速度增量趋于平稳(最大1 100 m/s).但该算法没有考虑采用多脉冲是否能够进一步减小燃耗需求.夏炎等[30−31]指出,标准Lambert 算法未考虑其他天体的引力摄动,因此,有必要在基础解上进行修正;但如何修正未作进一步研究.

吴岸明等[43]针对ASTROD-GW 任务的空间正三角形编队部署问题进行了研究.其轨道转移的起点为:两个航天器位于地球静止轨道朝向太阳的位置,第3 个航天器位于远离太阳的位置.吴岸明等[43]采用霍曼转移方式设计了3 个航天器进入日地L3 ∼L5 平动点的两脉冲控制.由于构形尺度较大(2.6 亿公里),该初始化过程单星需要的燃料消耗最小需要4.4 km/s,且转移时间超过3.2 a.

Hellings 等[44]针对OMEGA 任务的空间正三角形编队构形初始化问题进行了研究,提出了基于类圣杯低能轨道的方式,通过169 d 的轨道转移将3颗卫星发射至60 万公里目标轨道,然后再通过上面级减速的方式降低轨道近地点在186 d 内形成正三角形.

2.2 空间正三角形编队的构形保持与重构控制

构形保持与重构问题源自两个现实需要:一是由于入轨误差、控制偏差、系统故障以及摄动干扰的影响,编队构形随时间演化显著偏离标称构形;二是由于任务变更或调整,编队需变化为新的构形才能满足任务要求[39].其中构形保持控制主要用于构形小幅度调整,构形重构控制主要解决构形大范围调整.

LISA 任务是ESA“宇宙憧憬2015–2025” 计划中的第三次大型任务,预期于2034年发射.为解决LISA 空间正三角形编队构形的保持问题,Hechler等[45]从全流程任务角度进行了深入研究.研究结果表明,无法同时对3 个臂长进行稳定,只能在几年内稳定一个或两个臂长的变化率.Bik 等[46]为LISA 的三角形编队构形保持问题设计了双环控制算法,其中外环用于补偿精确建模的摄动干扰,内环采用比例微分(PD)控制实现各航天器的位置保持.黄文涛等[47]针对“天琴”任务的编队构形保持问题,提出一种基于虚拟编队的方法,采用四脉冲控制策略,实现了轨道中途修正.张立华等[10]、王继河等[11]对当前引力波探测的编队构形控制问题进行了深入调研和分析,认为:有限的机动控制能力是空间引力波探测编队构形控制的一个显著特征,应在考虑工程实际约束的前提下重点考虑组合式控制方案,充分发挥火箭上面级与卫星平台共同实现构形初始化与重构控制的能力.

针对引力波编队控制问题,中国科学院院士、“天琴计划” 首席科学家罗俊等[1]在2021年1月14日出版的论文中着重指出:“超远的星间距离(17 万公里)和仅装有µN 级微推力器等特点,使得“天琴”所涉及的空间正三角形星座动力学与控制问题有别于现在已经广泛研究的近距离编队和星座系统,对超远距离构形发散机理、机动能力受限下的高精度姿轨控制等方面提出了前所未有的挑战.”罗俊等[1]还指出,“天琴”编队任务应区分科学模式与非科学模式的不同,其中控制算法的设计应保证通过尽可能少的轨道保持实现构形长期稳定,在科学模式下要实现多星协调控制,在非科学模式下应确保燃料最优.上述这些分析既为研究目标提出了需求,也为如何开展超大型编队构形控制提供了思路.

开展编队构形控制研究是有非常迫切的现实需求的.随着欧洲LISA Pathfinde 技术验证星(2015年)、我国“太极一号”(2019)及“天琴一号”技术验证星(2019)等陆续成功发射,多星编队飞行任务逐渐被提上日程.2020年9月,中国科学院院士、“太极计划”首席科学家吴岳良说,中科院正在启动空间引力波探测计划第二步“太极二号”双星计划.而与此同时,“天琴”团队也计划2025年前后发射双星.由此可知,空间引力波探测编队的高精度构形控制需求变得越来越迫切[1,11].然而,综合现有国内外情况可知,当前空间正三角形编队构形的控制问题总体研究较少,且有限的研究结果无法满足引力波探测的任务要求[1−5,10−11].

2.3 研究建议和思路

2.3.1 空间正三角形编队的构形初始化控制

空间正三角形编队的构形初始化,是指3 个卫星从位于停泊轨道上的运载平台上分离进入任务轨道并形成正三角形构形的过程.可以考虑两种基本的构形构建方式:并行式和串行式,如图7所示.其中,并行式构建方式中,假设卫星携带较多燃料,可通过自主机动进行空间交会;三星从编队中心的运载平台上脱离后,同步进行轨迹转移,可以较短时间完成构形初始化.串行式构建方式中,假设运载平台具有较多的剩余燃料,可携带三星到达各自构形目标位置并依次释放,从而节省卫星的燃料使用,但构形构建时间略长.

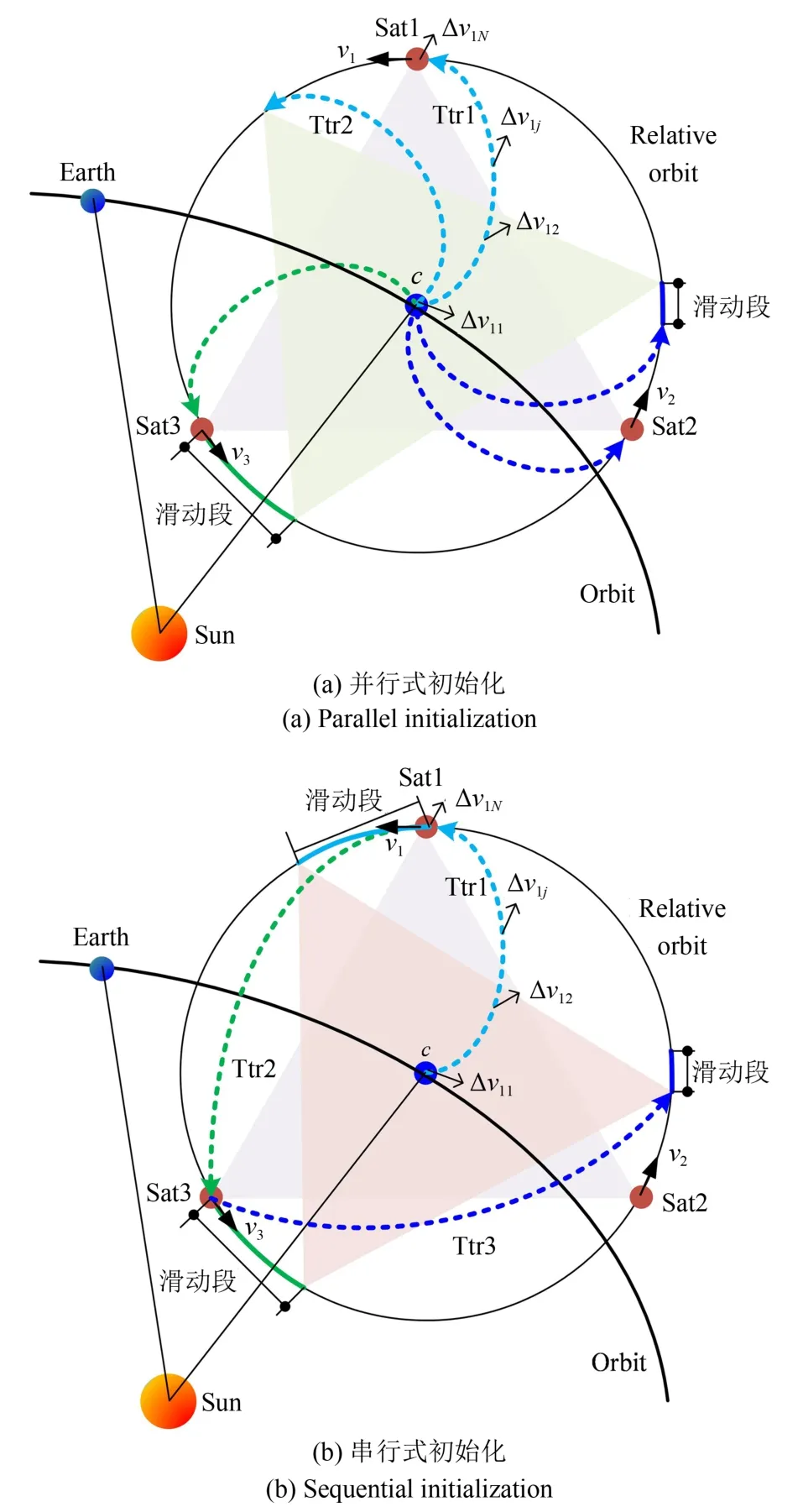
图7 空间正三角形编队的构形初始化Fig.7 Configuratio initialization of Space-based triangular formation

采用基于脉冲式的控制方式实现单星空间交会控制.脉冲控制模型通过CW 方程构建:给定N个脉冲施加时刻、初始相对状态、空间正三角形构形期望相对状态,则N个脉冲速度增量的表达式为:

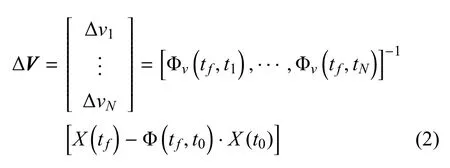
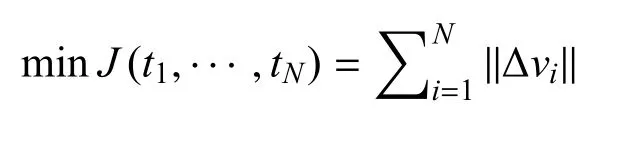
得到的轨迹称作多脉冲最优轨迹.具体优化时,可采用主矢量理论(primer theory)辅助判断最优性及改进方向,从而加速优化过程.但上述控制模型仅具有一阶精度,无法满足引力波探测对编队构形精确性的要求.因此,需通过微分校正(derivative correction)原理对多脉冲的具体数值进行进一步修正:

1)通过动力学精确数值积分获得给定控制下的末端状态偏差:

3)迭代计算得到最终精确控制.

空间正三角形构形要求初始相对状态满足严格稳定性条件,需要数值搜索才能得到.该稳定性条件对应初始化控制问题的终端相对状态.由于转移轨迹的不确定,该终端状态的精确数值事先未知;若将终端状态的实时搜索加入多脉冲优化,则因耗时巨大而无法实现.为此,可通过对空间圆离散化,对每个离散点采用如1.3 节的解析构造和数值优化方法,离线得到严格稳定的相对状态并构造数据库;然后对所有离散点进行三角配对形成初始化控制所需要的正三角形目标构形站位,如图8所示.构形初始化优化时,目标状态将从三角配对集合中抽取和搜索(算法3:构形三角配对算法).

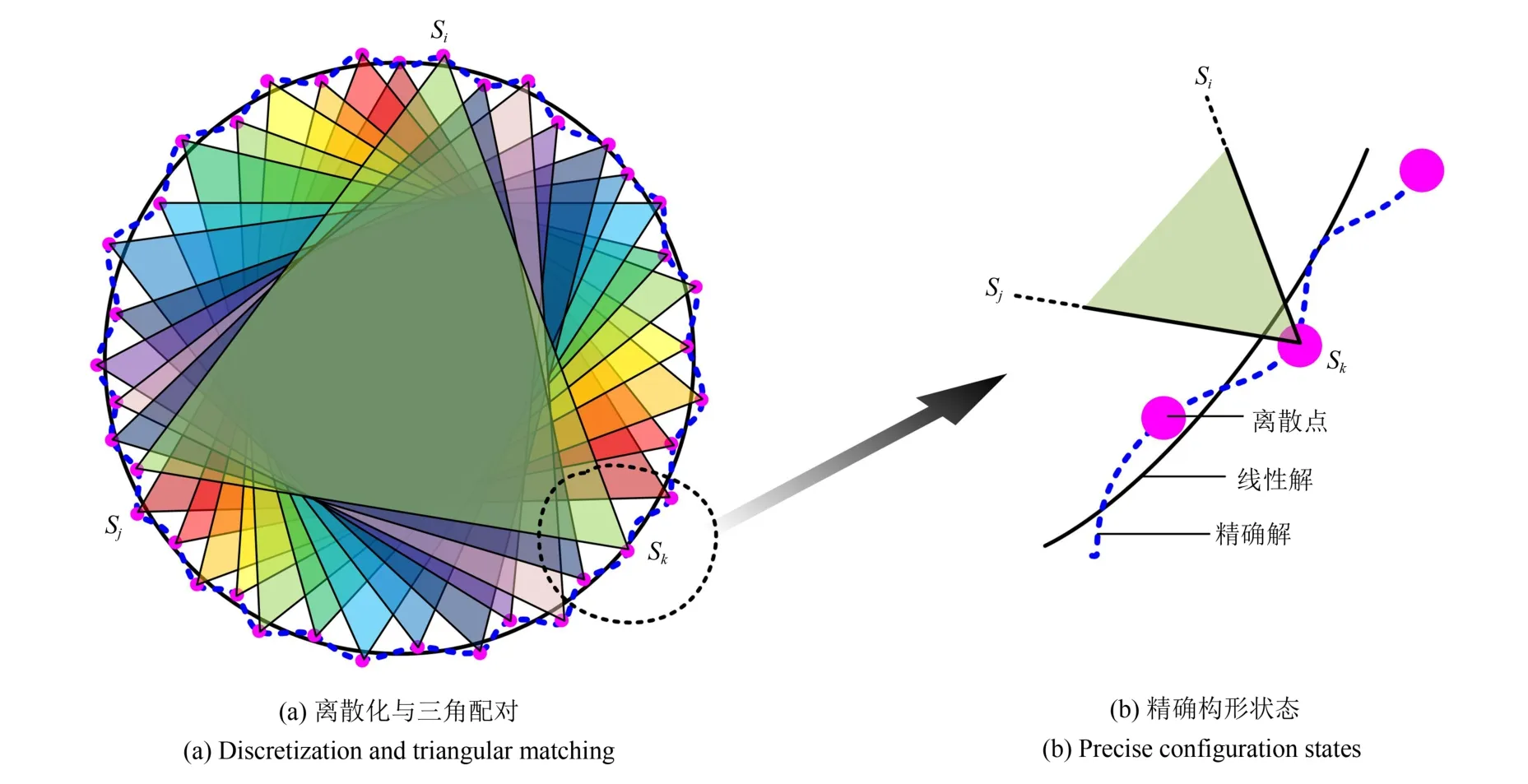
图8 空间绕飞圆的离散化及三角配对原理Fig.8 Discretization of circular relative motion and triangular matching principle

以上优化仅为交会轨迹优化,对应于确定的初始条件.实际上,引力波探测任务的起点可能发生变化,由此带来更多的优化余地.可对分离位置不在编队中心、停泊轨道偏离标称轨道两大情形进一步探索,如图9所示.

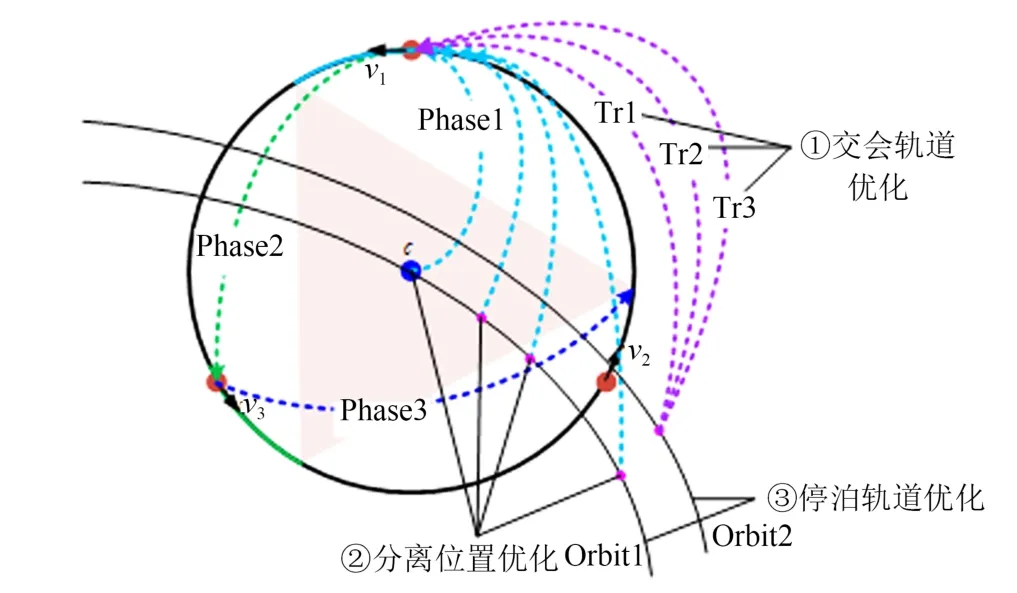
图9 空间正三角形编队构形初始化过程的优化问题类型Fig.9 Types of optimization problems in the space-based triangular formation configuratio initialization

2.3.2 空间正三角形编队的构形重构控制

空间正三角形编队的构形重构问题来源于3 种实际需求:1)摄动及误差积累导致的构形恢复需求;2)引力波探测频段更改带来的编队构形尺度调整需求;3)引力波探测方向更改带来的编队平面指向调整需求.考虑到引力波探测航天器实际配置约束,可在小推力连续控制模式下设计构形重构控制算法.

首先研究面向构形恢复的空间正三角形编队构形重构控制方法.由于空间正三角形编队的构形参数包括:中心位置c、臂长l、呼吸角α、编队平面倾角β 等,因此,构形恢复的基本类型也包括4 种,如图10所示.但真实情况下的构形变形,是以上4 种情形的组合,即同时包含多种构形参数的变化.构形恢复控制问题的求解思路为:1)确定目标中心c,由此计算参考轨道根数以及相对坐标系;2)确定构形基准相位角θ 并由此计算空间正三角形编队构形对应的3 个卫星的标称状态;3)通过最优化控制方法(例如LQR 控制)使每个卫星的相对状态误差消除为零.其中,目标中心c和构形基准相位角θ 的确定需要通过离散化优化实现(算法4:c−θ 优化算法),具体原理为:1)从构形发散后的中心附近按照一定间隔选取一系列待选中心点ck;2)在首个卫星相位角的附近按照一定间隔选取一系列待选基准相位角θk;3)然后,以所建立的两脉冲控制解析解作为燃料消耗优化指标,经数值搜索确定出最佳c∗和θ∗.

图10 空间正三角形编队构形恢复的4 种基本类型Fig.10 Four basic types of configuratio recovery for Space-based triangular formation configuratio

然后研究面向构形尺度调整的空间正三角形构形重构控制方法.构形尺度调整本质上与构形恢复问题相似,但不同之处在于前者具有较大范围的尺度变化,直接采用误差消除的反馈控制方法时会因推力受限而失效.因此,采用基于形状的轨迹优化方法(shape-based method)实现小推力作用下的构形重构,如图11所示.基本原理为:1)用一条参数化方程描述转移轨道,该参数化方程在起点满足初始状态约束、在终点满足目标状态约束;2)通过对参数化方程施加轨道动力学约束,反算出实现该轨道运动的控制函数.形状法计算效率高、优化方便,但采用何种形状(等价为参数化方程的形式)描述转移轨道,长期以来具有较大的随意性.

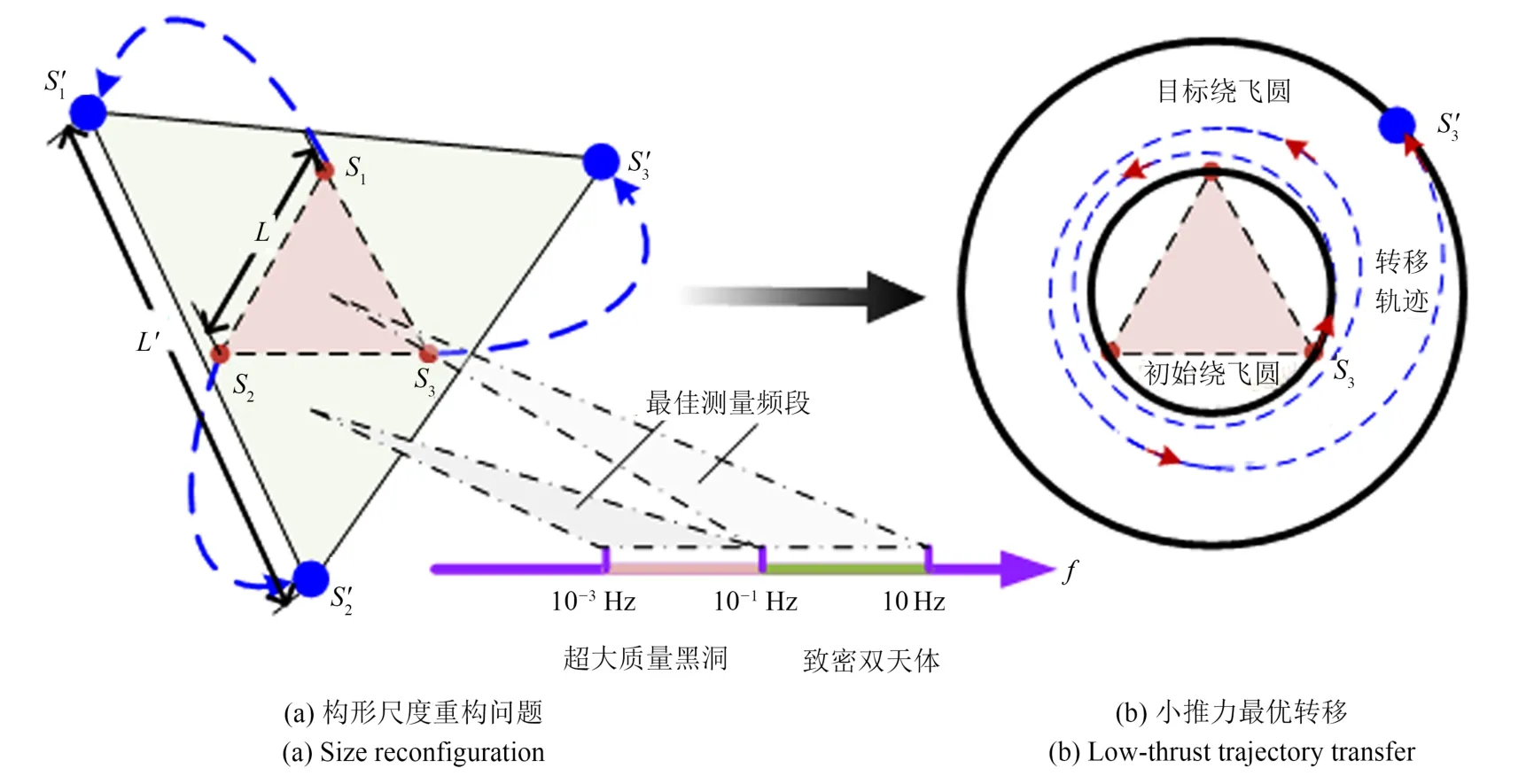
图11 基于小推力最优转移的空间正三角形编队构形尺度重构Fig.11 Size reconfiguratio of space-based triangular formation based on low-thrust trajectory transfer

笔者所在课题组近年来提出了一种基于Bezier(贝塞尔)曲线和引力场圆锥曲线方程相结合的复合函数形状法,能够充分利用自然轨道演化的内在性质,且能够通过贝塞尔曲线的高度自由性提高转移轨迹的最优性;相比以往的形状法展现出更优的性能.将上述方法改进后用于相对轨道运动问题(算法5:复合函数轨迹优化算法),此时基于复合函数形状法得到的构形重构转移轨迹可用式(3)描述:

其中:rrr(s)为转移轨迹的参数化方程,s∈ [0,1]为归一化的时间变量,rrrH1(t)和rrrH2(t)为初始绕飞圆对应的相对运动解析解、目标绕飞圆对应的相对运动解析解,BBB1(s)和BBB2(s)为贝塞尔曲线方程.这里s与时间变量t之间满足由用户定义的归一化关系:s=G(t).贝塞尔曲线形如其中bi,n(s)为贝塞尔系数,PPPi为待定参数.通过起点、终点的约束关系:可以得到完全平滑的转移轨迹.当贝塞尔曲线的阶数n较大时,多余的待定参数PPPi可作为优化变量,提升转移轨迹的最优性.一旦转移轨迹确定,则需要的控制可通过反解动力学得到:

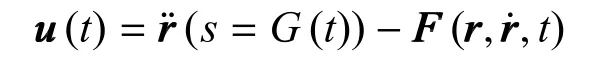
与初始化控制问题类似,构形重构时的目标相对状态也具有优化余地,因此,可采用算法3(构形三角配对算法),将目标构形上的相对状态进行离散化,从而通过数值优化搜索确定出最佳的重构目标.

最后研究面向编队指向调整的空间正三角形构形重构控制方法.编队指向调整问题的示意图如图12所示.与前述编队构形恢复、编队尺度调整两类问题不同,编队指向调整只能通过参考轨道(即编队中心所在的空间圆轨道)调整实现.这是因为,根据空间正三角形构形的形成机制可知,正三角形编队的平面与参考轨道平面的夹角β 只能为±60◦两种情形(但考虑摄动时,β 会发生小幅度≤1◦变化).因此,若要实现指向特定引力波方向的正三角形编队飞行,则必须调整编队中心所在的轨道.当在轨任务发生变化,需要从一个探测方向(γ,φ)转变为另一个方向(γ′,φ′)时,则按照以下流程进行计算:1)根据拟探测方向确定参考轨道的轨道根数;2)确定参考中心的位置c及对应的相对坐标系;3)再根据优选规则确定目标构形的基准相位角θ;4)按照研究内容一所建立的动力学模型和优化搜索方法,确定出目标构形对应的3 个卫星的位置和速度;5)最后采用算法5(复合函数形状法),设计得到各卫星的最优转移轨迹及控制函数.其中,上述计算流程中所说的中心位置c及基准相位角θ,需要通过优化以减小构形重构所需要的总燃料消耗,具体可采用算法4(c−θ 优化算法)进行求解.

图12 基于小推力最优转移的空间正三角形编队构形指向重构Fig.12 Direction reconfiguratio of space-based triangular formation based on low-thrust trajectory transfer

3 结论

本文对面向引力波探测的空间正三角形编队动力学机理及控制方法研究现状,作了系统全面的调研和分析.综合现有情况可知,空间正三角形编队构形的动力学形成机制、摄动演化规律及长期稳定策略已取得较为丰富的研究成果,能够支持特定引力波探测工程任务的设计需求.但现有动力学机理研究的不足在于缺少完整统一的理论框架体系,且已阐明的构形演化规律严重依赖数值计算结果,缺乏清晰的理论依据和物理解释.现有的引力波探测控制研究在单星无拖曳控制方面成果较多,而在三星正三角形编队控制方面成果较少.考虑到我国已明确提出在2035年前后实现空间引力波探测在轨实验的计划,多星编队的构形初始化、保持与控制将成为未来重要的研究方向.本文结合最新研究成果,揭示了正三角形编队动力学机理存在的若干研究空白以及潜在的解决思路,同时借鉴经典编队飞行理论,建立了引力波探测编队的构形初始化、保持与重构控制模型和原理.本文相关结果将为我国未来引力波探测的编队飞行任务设计与实施提供重要的理论基础.