软体机械臂高精度位姿线长测定方法

许嘉毅 刘红卫 张翔 黄奕勇

1．军事科学院国防科技创新研究院北京100071

软体机器人系统以及软体机器人部件、柔性机器人部件正在成为近年来领域内重点研究对象.在工业生产、人机交互、航空航天及军事作战等背景下的作用越发明显.军事航天领域在侦察、情报搜集等方面发挥着愈发重要的作用[1],使空间机器人具备干扰、捕获乃至摧毁的能力是近年的发展趋势.

软体机械臂作为软体机器人的重要部件.近年来的研究、设计及制造都有长足进步.软体机械臂驱动方式众多,结构各异,用途广泛,因此,每一类软体机械臂都有各自的运动学及动力学建模方法及控制方法.由于软体机械臂自由度近乎无限多,并且由于自身柔软的特性,使得要实时描述软体机械臂的位置姿态具有一定难度.需要一些高精度且易于实现的方法.

针对一种变截面充气柔性机械臂实际位姿测量定位的需求,提出利用测量线长进而得到机械臂位置姿态的一种方法,避免了传统测算过程中忽略机械臂渐收引起的测算误差,以及光电方法易产生干扰的问题.本方法利用已经铺设的驱动线,在不附加其他部件的前提下通过测量分段驱动线长度,并进行计算,最终得到精度较好的变截面机械臂位置姿态信息.

1 研究现状与测量方法简介

1.1 研究现状

刚性机器人广泛应用于工业领域,由刚性杆件和关节构成,会导致其与人类的接触可能是不安全的,与此同时,传统驱动机构缺乏顺应性也导致刚性机器人对于复杂环境的适应性降低.

软体机器人部件,例如机械臂,通常由柔性软体材料(例如硅胶)制成,这些材料可以变形并吸收碰撞产生的大部分能量,使得机器人具有连续可变形的结构以及类似肌肉的动力学特性,表现出前所未有的适应性和敏捷性.软体机器人能够实现大曲率弯曲和扭转,可以在狭窄的空间中使用[2];能够以连续的方式进行变形,模仿软体生物运动[3];能够适应复杂非结构环境,实现柔顺运动和操控物体[4];也可以在崎岖地形上移动并展现出很强的弹性[5].

软体机械臂的驱动方式有多种,一类是通过充入流体产生形变,康奈尔大学的球形软体阵列式驱动器[6].在此基础上增加纤维或刚性材料限制层,可制成人工肌肉,天津大学开发的一款新型模块化的气动人工肌肉[7].此外,诺丁汉大学的航空发动机检修机器人采用绳系驱动[8−10],中国科学技术大学利用基于形状记忆合金制作了一种驱动模块[11].近年来还出现了利用介电弹性体制成的柔性机器人[12].

1.2 测量方法

机械臂定位的方法主要以定位点测算和计算机视觉定位为主,二者各自具有不同的优缺点.定位测算方法通过测量末端相对位置矢量和各方向角,从而解算末端坐标.计算机视觉原理上和测距仪类似,随着图像识别等手段的发展,出现了通过测量RGB信息等手段,结合深度学习从而达到自动测算位置信息的功能.近年来广泛采用的激光测量方法是结合二者特点的一种测算方法[13].

文献[14]提出一种由形状记忆合金弹簧驱动的柔性机械臂.在对霍尔传感器进行标定测量时,采用了工业相机向两平面投影标定的方法.文献[15]针对铁水加注等钢铁冶炼的重型生产场景中,设计开发了基于三维激光扫描技术的加料机械臂精准定位系统.2020年,NATHAN S 等开发了一种新型软体机器人,该机器人不需要携带气源和气阀等供气装置,运动时通过控制机械臂节点位置,在达到整体变形、移动的目的同时,依据节点位置的移动,反推机器人各段的位置,进而确定机器人位置及姿态[16].

软体机械臂定位测量方式中,激光/超声波测距定位在测量长度、速度等方面精度高、响应快,但是对于环境有较高要求,例如在狭窄、曲折的环境中,激光无法绕过障碍物获得位置信息,再例如在太空环境下,超声波由于缺乏介质,完全失去作用.此外激光测量方法由于偏振系统的存在,将会在测量阶段引入误差[17];在机器视觉方法中,机械臂系统实际占用空间较大,且传感器布置在机械臂活动范围外,从而限制了机械臂系统的使用范围,并且,依靠无线电以及激光信号进行测量的方法容易受到干扰[18].

2 位姿线长定位方法

2.1 等效恒曲率测量关系推导

在恒截面机械臂段内,根据恒曲率模型,每一个恒曲率段上的弧线向弯曲平面的投影均为同心圆的一部分,如图1所示.由于机械臂段上下两截面均指向曲率中心,因此,该机械臂段内的弧段长度与距离曲率中心距离成正比.同理相对应点之间的连线也根据相似原理,其长度与距曲率中心距离成正比,如图2所示.由此可得关系式:

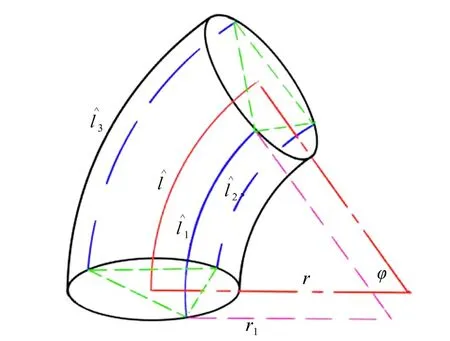
图1 恒截面恒曲率机械臂段Fig.1 Mechanical arm section with constant cross section and constant curvature

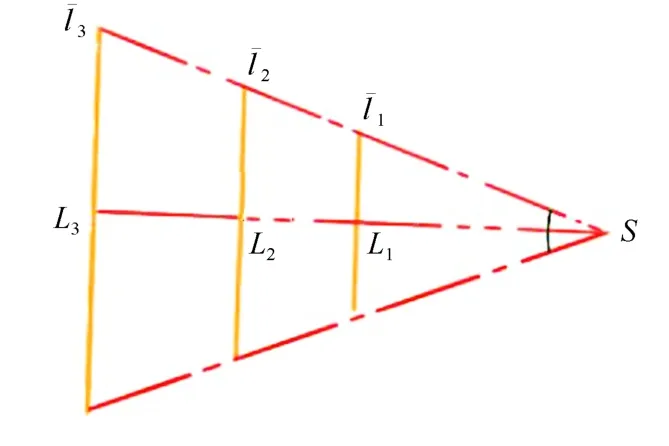
图2 等效线长在弯曲面投影Fig.2 Projection of equivalent line length on cur surface

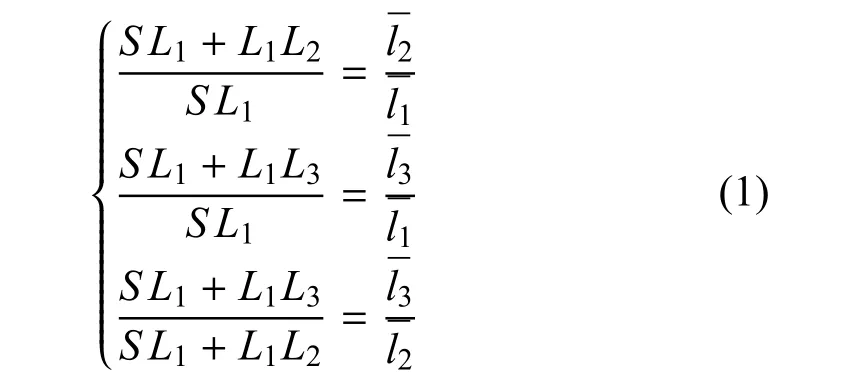
如图1所示,显然r1和r平行且所在扇形面具有相似性.r和r1的关系为

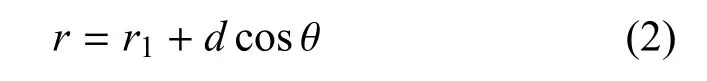
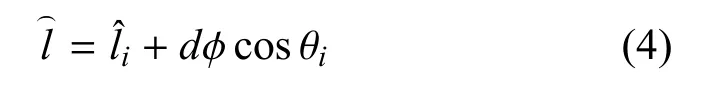
其中,θ1= θ,θ2= 120◦−θ,θ1= θ + 120◦.由于cos θ1+cos θ2+cos θ3=0,因此

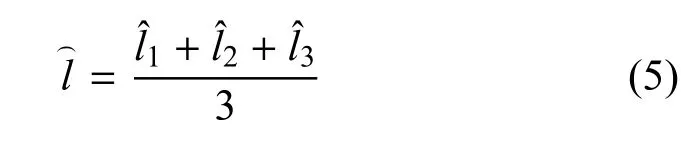
对于式(3)

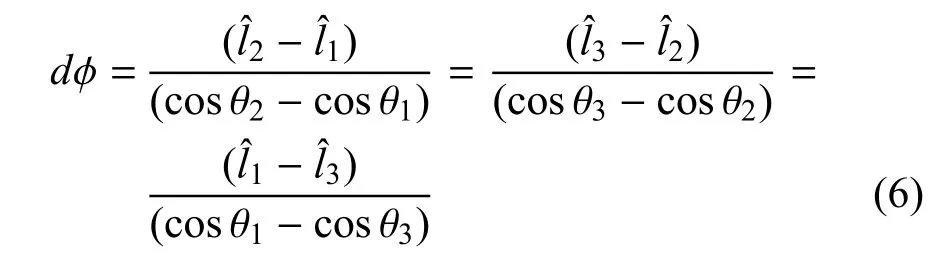
由于有关系:

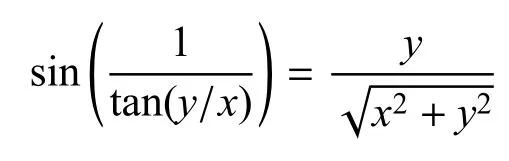
可得

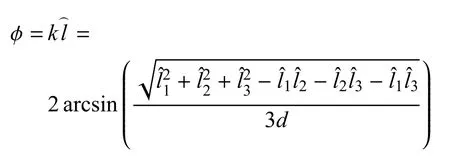
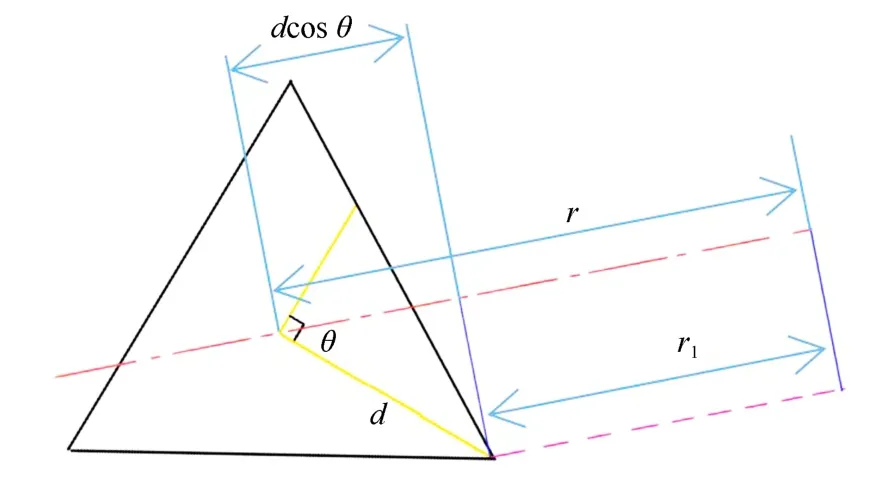
图3 弯曲段任意截面3 点向弯曲方向线投影Fig.3 Projection of three points of any section of bending section to bending direction line

2.2 变截面测量关系推导

在考虑真实情况下,例如Festo 仿生机械臂(如图4所示)并非恒截面积,而是有4.5◦渐收.在往常实验中,该机械臂在无外力施加的情况下并非恒曲率变形,而是随着距离根部越远曲率逐渐增加,因此,所有基于恒曲率模型的方法均不可采用.由于该机械臂每根波纹管由数段气囊单独构成,因此,可以选取每一个气囊段进行研究,并且可以认为在每个气囊段不受变曲率影响.为了得到变截面线长和等效线长之间的关系式,以弯曲方向为x轴,在该气囊段底部平面建立坐标系x′oy′,如图5所示.

图4 Festo 仿生机械臂Fig.4 Festo bionic mechanical arm

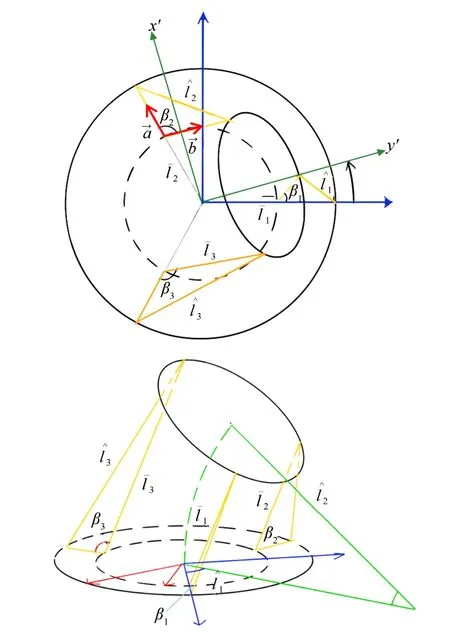
图5 气囊段弯曲示意图(以最短线长为x 轴方向)Fig.5 Schematic diagram of airbag segment bending(taking the shortest line length as the x axis direction)

以β2为例,引出两向量则在x′oy′中的坐标分别是:

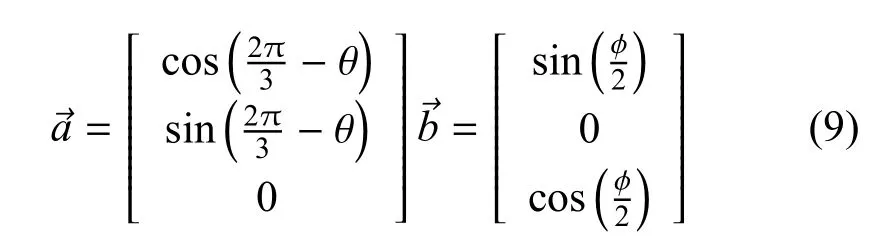
因此,可以写出β2的表达式:

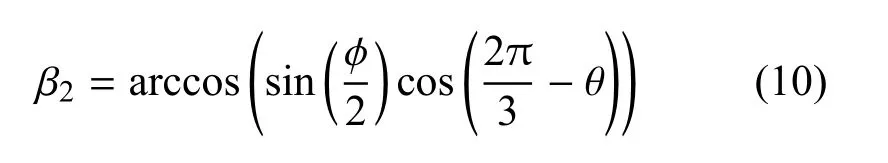
进而得到适用于所有位差角的计算公式:

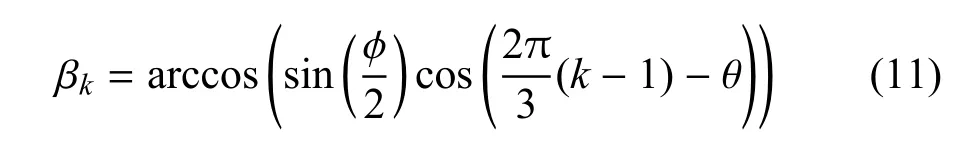
因此,根据余弦公式可得实际线长和等效线长之间的关系式:

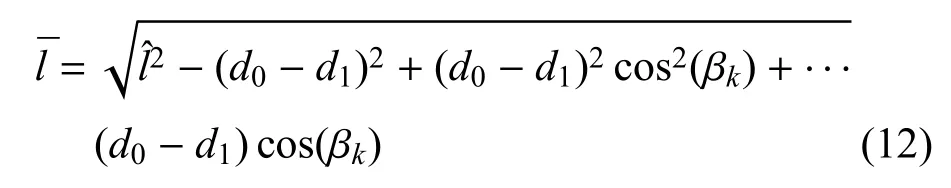
其中,d1为基座截面半径,进而全部弯曲方向和弯曲程度都可以写出:

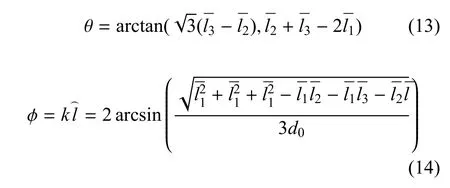
通常解算方法,由于实际线长和等效线长之间的关系式中包含β,而β 需要根据含等效线长的θ 和φ 解得,无法得到解析解,从而将β 近似为90◦,进而将实际线长和等效线长之间的关系式省去最后两项.

为了提高求解精度,采用不动点迭代的方法,计测量得到的实际长度为迭代初值,根据式:

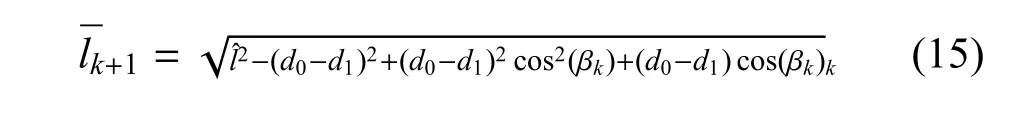
以当前状态测量线长为初值进行迭代.最终可以得到机械臂段确定末端位置所需的θ、φ、¯l3 个参数.其中,迭代流程如图6所示.

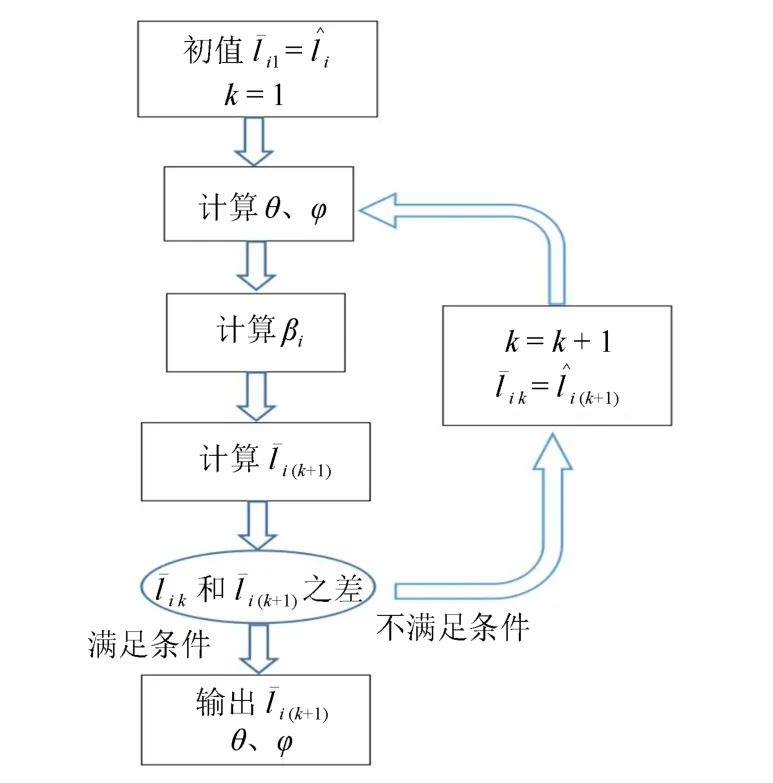
图6 本方法迭代流程Fig.6 The iterative process of the method

3 测算实例

在实际应用中,某型机械臂底端基座半径100 mm,按照4.5◦渐收,则按照上述方法测算得到其每一段的位置姿态(见图7(a)).其中,等效线长迭代计算前后误差限制设置为不大于0.000 001 mm,最终迭代次数为7 次.图7(b)展示了本方法和恒曲率模型方法相对实际机械臂位置姿态的测算结果对比.

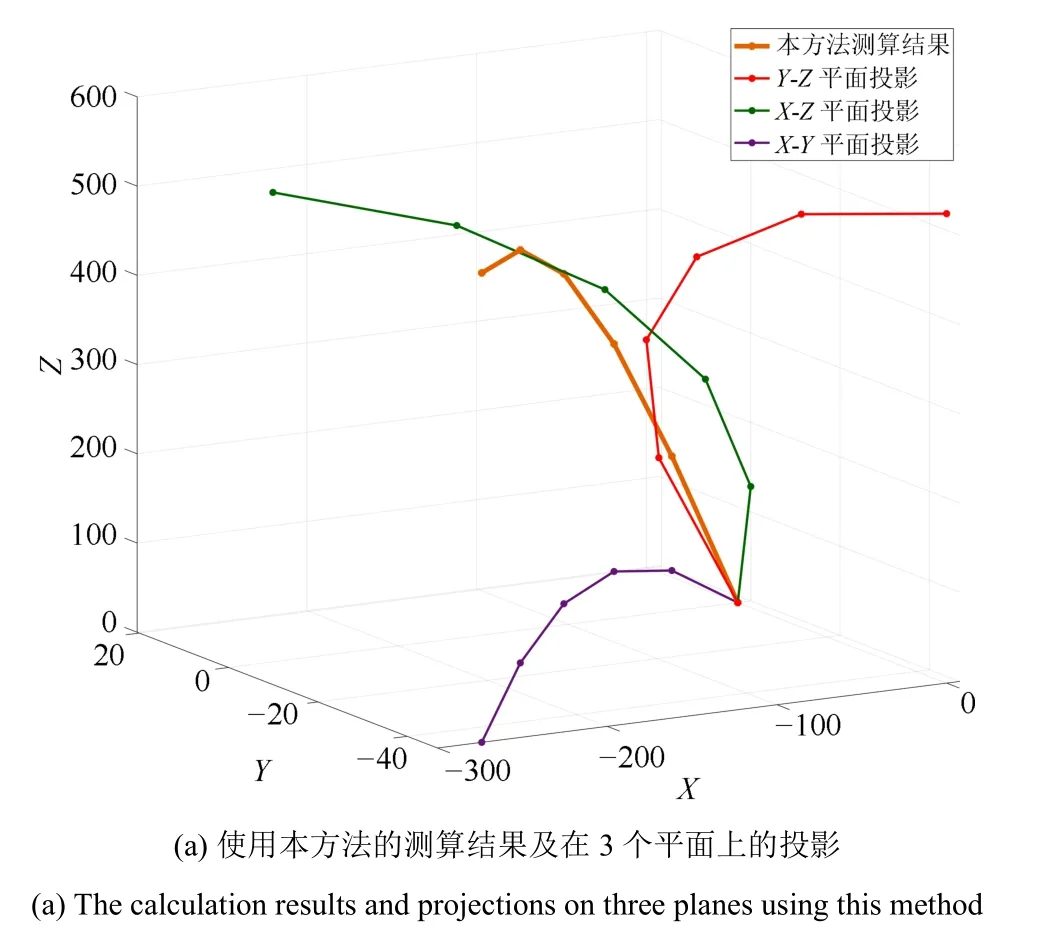
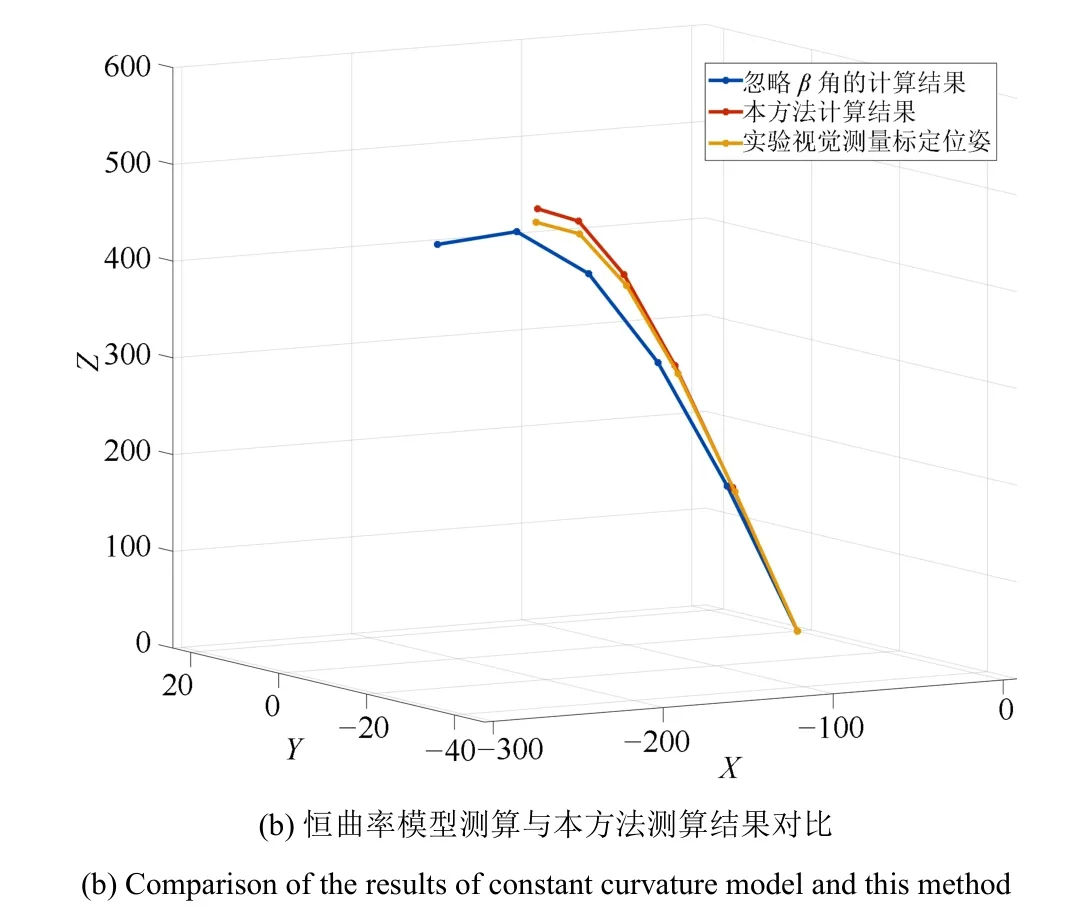
图7 测算结果Fig.7 Measurement results

4 结论

本文对于变截面机械臂通过测量驱动线缆或测量线缆的长度,代入定位方法解算可获得精度较高的末端位置确定,并且在θ、φ、¯l3 个参数的求解过程中采用数值迭代,解决了由于忽略β 角带来误差的问题.但是由于拉线的测量本身对计算会带来相对较大的误差,一部分软体机械臂外表不依靠拉线进行辅助驱动,其中,有一部分无法在臂表面附着测量线,因此,该方法在实际使用中依旧存在些许困难,亟待解决.