动静干涉下压气机叶轮气动激励与振动分析

马朝臣，洪舟振森，张虹，吴新涛 (.北京理工大学 机械与车辆学院，北京 0008; .中国北方发动机研究所 柴油机增压技术重点实验室，天津 300400)

车用涡轮增压器可以利用内燃机的废气能量对进气进行增压，提高内燃机的动力性及经济性等，因而得到了广泛的应用.但叶轮在工作过程中承受着动静干涉及流场自身不稳定性带来的非定常气动激励的作用，会发生高频振动甚至共振，存在着疲劳失效的风险，因此有必要对叶轮的非定常气动激励及由此引发的振动进行深入分析.

在离心压气叶轮气动激励方面，祁明旭等[1]对使用无叶扩压器的离心压气机内部流场的压力波动频谱特性进行了分析，结果表明，在高转速近失速工况下，长短叶片压力面前缘以及尾缘叶顶附近压力波动主要受蜗壳周向不均匀的影响.曹林等[2]针对车用无叶扩压器半开式离心压气机叶轮分析的结果表明，位置越靠近蜗壳压力波动幅值越大.李杜等[3]研究了90°进气弯管带来的进气畸变对压气机内部流动的影响，发现弯管主要影响叶轮进口以及叶轮前缘叶顶的静压频谱结构.王磊磊等[4]分析了有180°进气弯管的离心压气机的内部流场.陈山[5]研究了有进口导叶的压气机流场.在压气机叶轮受非定常气动激励发生强迫振动的方面，PHILIPP等[6]以及MISCHO等[7]研究了有进口导叶的离心压气机叶轮在失速工况下的动应力，前者的结果表明叶轮在7个失速团作用下发生1阶共振时，动应力幅值小于材料疲劳极限，后者主要对比分析了流固耦合数值计算结果与试验结果，说明了使用数值方法分析叶轮振动问题的有效性.

目前，针对压气机叶轮气动激励以及振动的研究大多相互独立，无法反映两者间的关系.而流固耦合数值计算也多停留在单向稳态流固耦合阶段，难以获得非定常气动激励及叶轮振动的特征.

本文将采用单向瞬态流固耦合的方法，定量地分析共振工况叶轮与进气弯管和蜗壳动静干涉作用下的非定常气动激励特征及相应的结构瞬态响应特征.

1 流固耦合计算模型

所研究的涡轮增压器用于某V型8缸柴油机，增压器压气机端前为进气三通管.压气机叶轮直径114.3 mm，共有8组长短叶片，材料为变形铝合金2A70，采用无叶扩压器.采用计算流体力学(CFD)计算软件与有限元(FEM)计算软件进行单向瞬态流固耦合的计算.

1.1 CFD模型

为考虑流动边界层的影响，在壁面附近划分5层三棱柱网格层，第一层高度为0.01 mm，增长率为1.2，其余网格均为四面体网格.计算域网格模型如图1所示.

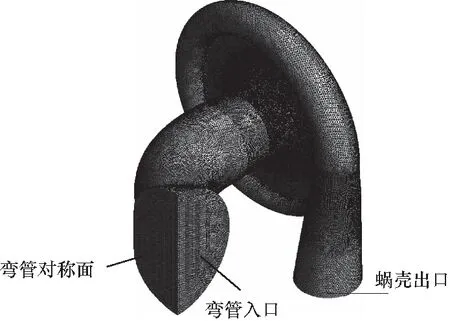
图1 CFD计算网格模型Fig.1 CFD calculation mesh model

计算域的入口设置为总温总压边界，出口设置质量流量，工质为理想空气.湍流模型采用k-ε模型，壁面函数采用Scalable.转域与静域间交界面的参照变换选用Frozen Rotor方法.计算域中存在叶轮固体域，叶轮的叶片面、Hub面以及锁紧螺母面为流固耦合换热面.在三通管的对称面上设置对称边界条件.在流体域中，除流固耦合面外的所有面均为无滑移光滑绝热壁面；在固体域中，除流固耦合面外的其他面均指定绝热边界条件.CFD计算的收敛准则为均方根残差小于10-4，守恒目标为0.005.

采用稳态计算，进行网格无关性分析与仿真结果有效性验证.网格无关性分析计算结果如表1所示.中等网格相对于精细网格总压比偏差为0.16%，总对总等熵效率偏差为0.23%，满足要求，由于计算资源较为充足，故采用精细网格进行计算.进行有效性验证的CFD模型不包含进气弯管，计算工况进气总温为17℃，进气绝对总压为102 kPa，折合转速70 000 r/min，数值结果与试验值的对比如图2所示.最大总压比误差为4.6%，最大效率误差为6.9%，均出现在大折合流量处.最大误差满足要求，因此仿真模型气动性能计算结果可信.

表1 网格无关性分析

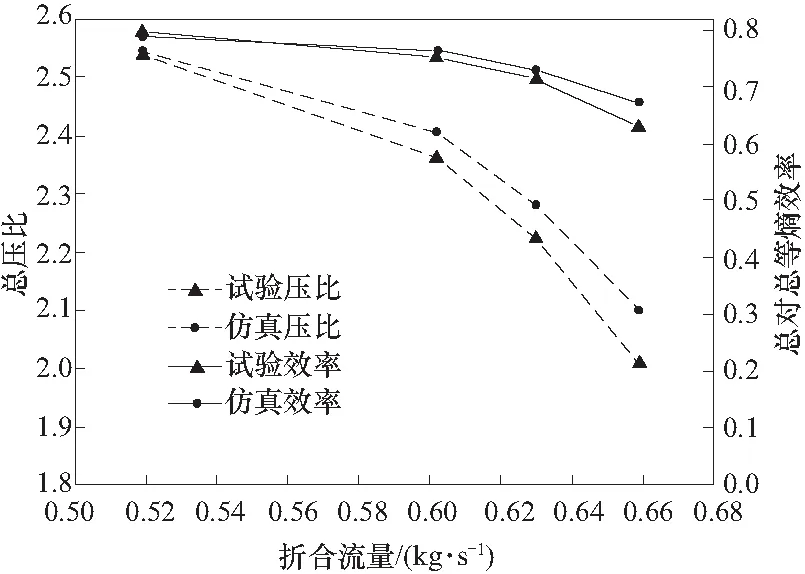
图2 仿真结果有效性验证Fig.2 Validation of simulation results

1.2 FEM模型

叶轮有限元计算网格选用二阶四面体单元，在轴孔处施加Remote displacement约束，指定径向位移为0，轴向旋转角度为0；轮背凸台处施加轴向位移约束.考虑大变形带来的几何非线性的影响.叶轮载荷来自于CFD计算结果，叶片面和Hub面为流固耦合面，接收气体压力载荷.2A70弹性模量为72 GPa，泊松比为0.33，密度为2 800 kg/m3，屈服强度为353 MPa，抗拉强度为412 MPa.

以离心应力和前30阶固有频率为指标，进行网格无关性分析，最终选定叶轮网格数为442178.网格模型及面名称示意图如图3所示.

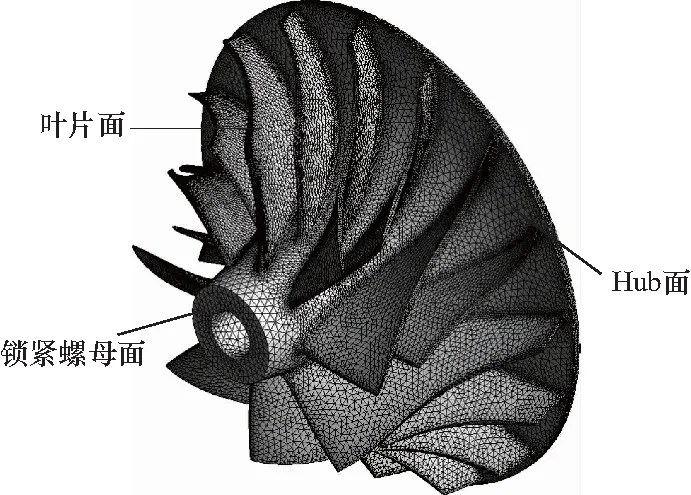
图3 有限元网格模型及面名称Fig.3 Finite-element grid model and the surface name

1.3 单向瞬态流固耦合设置

通过下文模态分析获得的叶轮共振转速为92 312 r/min，在此转速下进行单向瞬态流固耦合计算.

CFD计算进口总温15 ℃，进口总压101.325 kPa，出口真实流量0.741 9 kg/s.去除CFD模型中的叶轮固体域，所有壁面均设置为绝热面.动静交界面参照变换采用Transient Rotor Stator方法.叶片面和Hub面与FEM模型上相应的面耦合，向其传递气体作用力载荷.瞬态项采用2阶向后欧拉格式.其它设置与1.1节一致.FEM模型叶轮的约束与1.2节完全一致，施加转速载荷92 312 r/min，叶片面与Hub面从CFD模型中相应面插值获得气体作用力载荷.阻尼采用Rayleigh阻尼，α=0，β=2.652 6×10-8.瞬态结构的求解采用直接积分法.瞬态流固耦合时间步长设置为4.0623 μs，满足流场与结构场瞬态计算的要求.在每一个时间步结束后流场向结构场传递压力载荷.计算总时长为0.007 157 77 s，即叶轮转动约11圈.

叶轮转动起始位置及扇区编号如图4所示，叶轮沿z轴负方向旋转，x轴正半轴为弯管内侧半圆对称线，而负半轴为外侧半圆对称线.

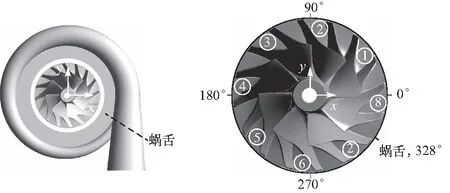
图4 叶轮转动起始位置及扇区编号Fig.4 Impeller rotation starting position and sector number

2 模态分析与共振转速

模态分析的阻尼和约束与1.3节一致.根据模态计算结果，叶轮存在着许多重频及密频模态.这些模态在振型上存在着相似性，仅有节径数的不同，节径数等于相邻扇区对应点振型分量反号次数的一半.

叶轮2阶模态周向振型云图如图5所示，2阶模态主要表现为长叶片的1节线振型，所有相邻扇区共存在着2次反号，因此节径数为1.1阶到11阶模态均为长叶片1节线振型，仅有节径数不同，据此可以将它们划分为1阶模态族.叶轮2阶模态族为短叶片1节线振型，3阶模态族为长叶片2节线振型与短叶片1节线振型.1阶模态族0节径模态的模态应力如图6所示，可以看出，长叶片的前缘模态应力值较大，因此叶轮在实际的气动载荷下发生1阶共振时，该位置的动应力值可能较大.

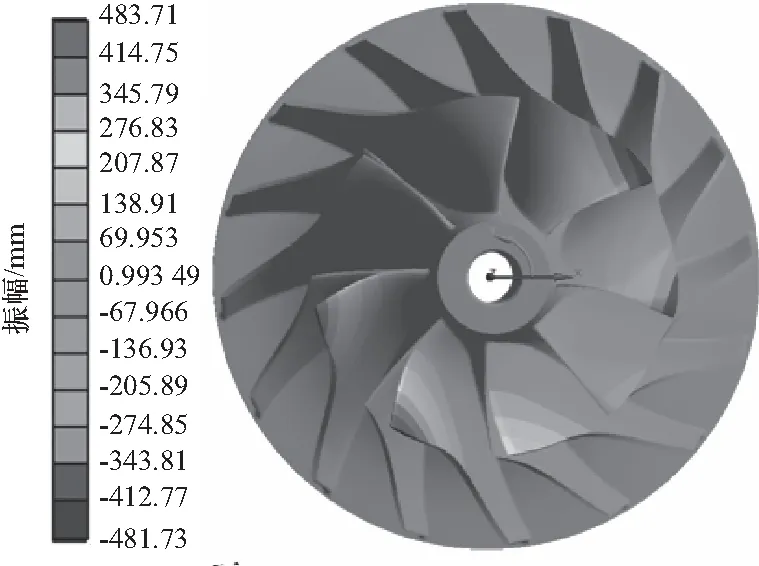
图5 2阶模态周向振型云图Fig.5 Circumferential mode shape contour of the 2th mode

图6 1阶模态族0节径模态的模态应力Fig.6 Modal stress in the 0 nodal diameter mode of the first order modal family

在叶轮机械中，只有激励阶次与某阶模态的节径数满足式(1)时[8]，该阶模态才会被完全激发,即

(1)

式中:n，NV，NB，d分别为激励阶次，导叶数，扇区数与节径数;Z为整数集；对于仅有进气弯管和蜗壳的叶轮而言，可认为NV=1，而节径数始终满足d≤NB/2.

根据离心应力作用下的模态频率结果绘制出的Campbell图如图7所示.图中激励的阶次用引擎阶次(engine order)nEO来描述，它等于激励的频率与叶轮转速频率之比.叶轮的工作转速区间为40 000 r/min～87 000 r/min，在考虑了激励的阶次与模态节径数的匹配后，1阶模态族共振点如图7中圆点所示.本文为了对最危险工况进行考虑，选择的共振点为4阶气动激励诱发的1阶4节径模态共振，此时叶轮工作转速为92 312 r/min，超出标定转速6.1%.

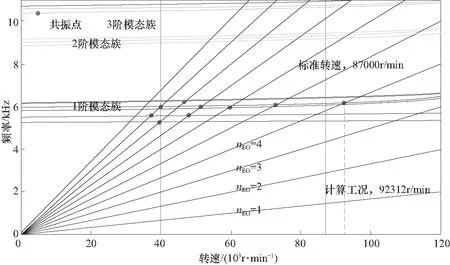
图7 Campbell图Fig.7 Campbell diagram

3 非定常气动激励分析

3.1 时域分析

从图8可以看出，受非轴对称蜗壳几何的影响，在叶片尾缘及轮盘边缘，距离蜗舌较近的位置其静压较大.其他时刻叶轮表面的静压分布均与图8相似.而在弯管出口截面上，其内侧静压较低而外侧静压较高.在7号长叶片的前缘、约20%弦长位置和尾缘处共取18个测点观察其静压时域波动，测点位置如图9所示，由于20%弦长位置穿过吸力面前缘低压区，因而在此布置测点.

图8 某时刻叶轮表面静压云图Fig.8 Contour of static pressure on the impeller surface at a certain moment

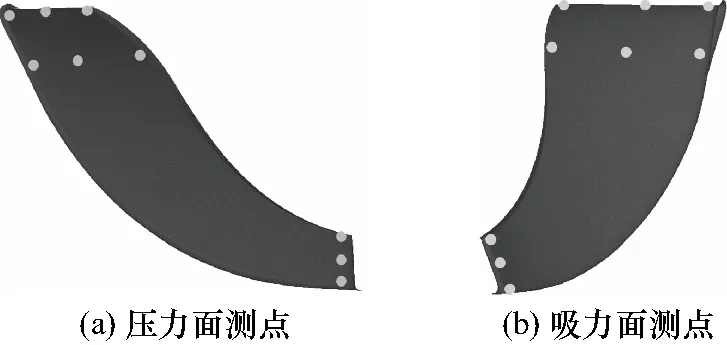
图9 测点位置示意图Fig.9 Schematic diagram of the location of the measuring points

图10中蜗舌标记的为相应弦长位置吸力面叶根测点经过蜗舌时叶轮的转动角度，高压区与低压区标记的为该测点经过弯管外侧与内侧对称线时叶轮的转动角度.

从图10 (a)中可以看出，长叶片前缘压力面的静压波动表现为峰值，而吸力面的静压波动表现为谷值.由于叶片前缘与蜗舌之间的流向距离较大，蜗舌带来的流体速度变化以及压力波动需要经过一定时间才能传播到叶片前缘，因此波动既可能来自弯管的影响也可能来自蜗壳的影响.

从图10 (b)中可以看出，①压力面和吸力面的静压波动均为峰值，测点在经过低压区后出现峰值，且出现时间与测点经过蜗舌的时间表现出了良好的一致性，由此判断波动主要由蜗舌引起.②压力面对于蜗舌干扰的响应十分迅速，而吸力面表面的静压响应虽然与前者几乎同时开始发生变化，但是变化速度要更慢.

对比图10(a)和(b)可以发现，在叶片表面静压开始波动时，其压力面与吸力面对应点处的静压差总是先增大后减小，这会导致叶片承受由压力面指向吸力面的动态气体作用力，使叶片发生振动.以叶片经过蜗舌的时间为起点，气体作用力会先出现在叶片尾缘，后出现在小弦长位置.

图10 测点处静压随叶轮转动角度的变化Fig.10 The variation of static pressure at the measuring points with the rotation angle of the impeller

以最后2圈中测点静压最大值与最小值之差作为时域压力波动，表2为18个测点压力波动的大小.从表中可以看出，尾缘静压波动比前缘大，压力面的静压波动比吸力面大，大叶高位置波动比小叶高位置大.最大静压波动出现在尾缘压力面叶顶处，为91.0 kPa.由于尾缘波动大于前缘，而其又由蜗舌引起，因此可以判断在最大值上，蜗舌引起的波动要大于弯管引起的波动.

表2 测点静压时域波动

3.2 频域分析

以叶轮转动最后2圈为采样周期，压力面尾缘叶顶处测点的静压幅值频谱图如图11所示，其它测点的静压频谱结构与图11基本一致.从图中可以看出，测点处1～4阶激励的幅值随着引擎阶次的增加而迅速减小，而在4阶及以上气动激励处，幅值随阶次的变化则较小，高阶的气动激励幅值甚至可能大于低阶气动激励.

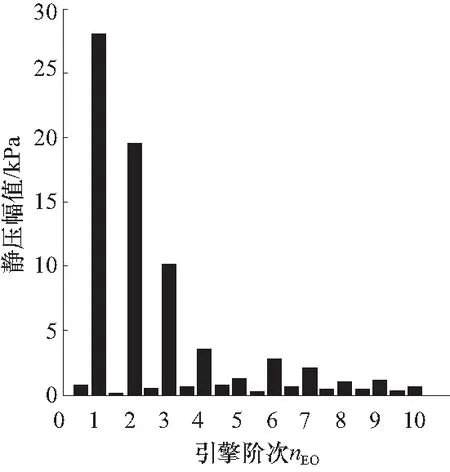
图11 压力面尾缘叶顶测点静压幅值频谱图Fig.11 Spectral diagram of static pressure amplitude at the tip measuring points of the trailing edge of the pressure surface

对叶轮表面每一个节点做快速傅里叶变换(FFT)，并绘制出气动激励幅值PA的云图，受制于篇幅，这里只展示4阶的结果，如图12所示.叶轮1阶和4阶气动激励均主要作用于叶片区域，最大值均位于长叶片吸力面约30%弦长位置的叶顶处.2阶和3阶的最大值则出现在叶片尾缘.

结合图12以及未给出云图前3阶气动激励幅值，在长叶片约30%弦长位置以前，各阶的气动激励幅值都较低.根据图5可知，叶轮1阶模态族振型的最大位移在长叶片前缘叶尖，当激励位于振型分量较大的位置时会对模态起到很好的激发作用，而前4阶气动激励幅值在1阶振型分量较大的长叶片前缘三角形区域均较小，因此诱发的叶片振动可能较小.

图12 4阶气动激励幅值云图Fig.12 Contour of 4th order aerodynamic excitation amplitude

4 叶轮振动响应分析

4.1 位移分析

以叶轮不承受任何载荷时各节点的位置为原点来衡量位移，3个正交方向上位移分量的矢量和定义为总位移.最后2圈内节点最大总位移与最小总位移之差作为节点动位移dD，动位移云图如图13所示.可以看出，对叶轮单扇区而言，最大动位移出现在长叶片前缘叶尖处.单扇区动位移的分布与叶轮的1阶模态族振型近似.还可以发现，相邻扇区长叶片的振动剧烈程度并不相同.这是因为非0节径的模态各扇区振动的大小存在着差异，而叶轮实际的振动过程又有许多同阶不同节径的模态以及不同阶的模态不同程度地参与其中.

图13 动位移云图Fig.13 Contour of dynamic displacement

从图14可以看出，①在叶轮转动一周的过程中，7号长叶片叶尖位移有大约4次波动，这一频率与叶轮的1阶固有频率是吻合的.②相邻叶片的叶尖位移表现出一定的反相特征，这一振动形态与叶轮1阶4节径模态的振型是一致的，说明4节径模态得到了激发.

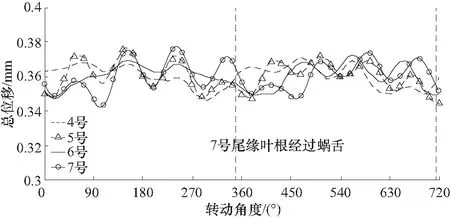
图14 4～7号长叶片前缘叶尖总位移随转动角度的变化Fig.14 Total displacement variation of the leading edge tip of No.4～7 long blades with impeller rotation angle

以最后1圈为采样周期，7号叶片总位移幅值频谱图如图15所示.结合3.2节图11可以发现，1～3阶总位移的幅值不断减小是因为对应频率的气动激励幅值不断减小，因而气动激励作用下强迫振动的程度也在减小.4阶谐波处峰值的出现说明叶轮发生了共振，但是由于4阶气动激励的幅值远小于1阶气动激励，因此1阶总位移谐波的幅值比4阶要大.在5阶谐波及以后，则因为气动激励较小以及没有与之对应的模态，使得振动程度较小.

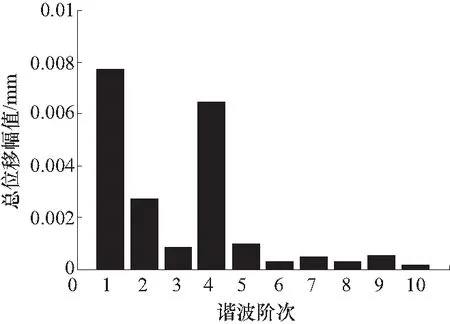
图15 7号长叶片前缘叶尖总位移幅值频谱图Fig.15 Spectral diagram of the total displacement amplitude of the leading edge tip of the No.7 long blade

4.2 应力分析

叶轮等效应力分布主要受离心载荷影响，最大等效应力出现在近背盘轴孔处.以最后2圈内等效应力最大值与最小值之差作为动应力，动应力云图如图16所示.可以看出，①对于单扇区而言，最大动应力出现在长叶片吸力面近前缘，出现位置与1阶模态族模态应力吻合.②从整周叶轮来看，相邻扇区的动应力并不一致，结合图13可以看出，动位移较大的叶片其动应力也较大.在长叶片吸力面前缘、吸力面尾缘以及压力面尾缘叶根这些位置，由非定常气动载荷引起的动应力较大，多在6 MPa以上，由离心应力引起的平均应力也较大，因此是发生疲劳失效的危险点.

图16 动应力云图Fig.16 Contour of dynamic stress

由于变形由应变累积而成，应变与应力满足线弹性关系，因此长叶片吸力面前缘的等效应力时程曲线与图14基本一致，故此处略去其应力时程曲线及频谱图.

5 结 论

采用单向瞬态流固耦合的方法，针对有进气弯管及蜗壳的模型，讨论了共振工况叶轮表面的非定常气动激励特征，以及此激励下叶轮的振动特征.主要结论如下.

① 长叶片在经过蜗舌后会承受由压力面指向吸力面的先增大后减小的动态作用力，且动态作用力先出现在叶片尾缘后出现在叶片前缘；长叶片尾缘静压波动比前缘大，压力面的静压波动比吸力面大，大叶高位置波动比小叶高位置大，在最大值上，蜗舌引起的波动要大于弯管引起的波动；叶轮表面1～4阶气动激励的幅值随着阶次的增加而迅速减小.

② 叶轮在所选共振工况处振动时，最大动位移出现在长叶片前缘叶尖，最大动应力出现在长叶片吸力面近前缘.4阶气动激励诱发了叶轮的共振，但是由于4阶气动激励幅值远小于1阶的幅值，因此叶轮振动的4阶谐波幅值要小于1阶谐波幅值.

③ 长叶片吸力面前缘、吸力面尾缘以及压力面尾缘叶根等部位由离心应力引起的平均应力较大，在共振工况下，动应力也相对较大，因此是疲劳失效的危险点，叶轮易在这些位置萌生疲劳裂纹，并由此发生疲劳断裂.