基于贝叶斯网络的MEMS安全系统可靠性分析

娄文忠, 赵悦岑，冯恒振，孙毅 (1. 北京理工大学 机电学院，北京 100081； 2. 北京理工大学重庆创新中心，重庆 401120)

引信作为弹药系统中的重要组成部分，是武器系统发挥终端毁伤效应的最终执行器，其可靠性大大影响了武器系统的作用效果[1]. MEMS安全系统是MEMS引信微系统中的核心器件，由许多元件组成，结构复杂，工作环境特殊，具有高过载、高转速、高速度的特点，并且作用过程是一次性不可逆的，故失效过程是多效的，这也提高了对MEMS安全系统可靠性的要求. 目前可靠性分析通常采用故障模式及影响分析(FMEA)、故障树分析(FTA)、贝叶斯网络(BN)、成功流(GO)等方法，而可靠度计算方法大体可以分为3大类：Monte-Carlo法(蒙特卡洛法)及其改进方法、边界法和近似方法. 近年来，较多学者对引信系统进行了可靠性分析，周利东等[2]应用混合Beta先验分布的Bayes方法针对小样本引信可靠性进行了分析；TU等[3]利用CAE软件对引信安全系统可靠性进行了仿真，建立了安全系统可靠性分析的流程；SHARP等[4]通过建立故障树，对高可靠性的引信进行了分析，并提出了优化方案. 由于引信工作的特殊性，其零件可靠度多为从现有试验中统计数据或从生产检验中获得数据，因此置信度不高，对于不同设计机构无法得到准确的可靠度，导致故障树顶事件计算不准确[5]. 针对以上问题，本文运用故障树分析法，建立了MEMS安全系统故障树进行定性分析，并根据故障树底事件建立功能函数，通过蒙特卡洛方法求解底事件可靠度. 然后，将故障树转化为贝叶斯网络，更加准确快速求得系统的可靠性，并计算各底事件的重要度，为MEMS安全系统设计优化提出方案.

1 安全系统FTA模型建立

故障树分析法是以系统失效模式作为顶事件，从上至下分别为导致系统失效的原因. 本文以图1所示的一种基于混合工艺具有远距离解除保险功能的低成本弹头引信安全系统方案为例，其MEMS安全系统分为离心保险机构和电火工保险机构的双保险设计.

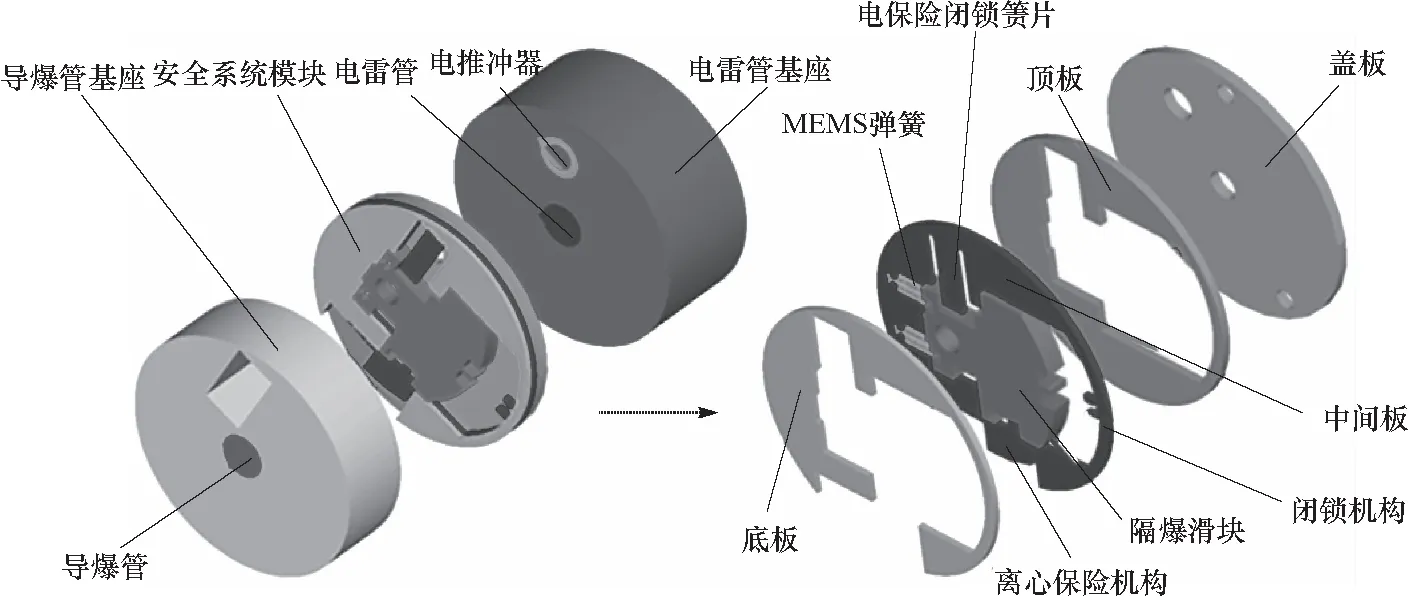
图1 某小口径弹用混合工艺MEMS安全系统结构图 Fig.1 MEMS S&A device structure for a small caliber missile

在小口径弹药的发射状态下，MEMS安全系统在后坐过载和离心力的作用下，离心保险机构释放隔爆滑块. 由于发射状态会持续一段时间，离心保险机构将保持在解保状态. 当弹药飞行一定距离时，电动推冲器起作用，推动电保险闭锁簧片，并使之变形，隔爆滑块被释放. 在离心力的作用下，隔爆滑块克服MEMS弹簧的拉力在平面内运动. 运动一段距离后，紧随着闭锁机构工作，对隔爆滑块实现闭锁定位，从而引信进入准备状态. 由MEMS安全系统的工作原理可以发现，MEMS安全系统整体能否完成既定的功能，主要受离心保险机构和电火工保险机构的影响[5]. 根据弹药的飞行特性可知，弹药从出炮口后飞至目标前始终以一定的转速前进，且旋转弹药所受的空气阻力可以忽略不计，因此弹药以最大转速抵达目标点. 当电火工保险机构、弹簧及离心保险机构均能可靠工作时，即使闭锁机构发生失效，隔爆滑块在离心力的作用下也能保持传爆孔与导爆孔的对准状态，故不考虑闭锁机构失效[6]. 其中，离心保险机构属于弹簧结构，为提高安全系统的可靠性，采用两个弹簧的冗余设计，只有当两个弹簧均未可靠作用时，才会影响整个安全系统的可靠性. 电火工保险部分主要可能故障在电推冲器上，如电推冲器不能正常作用，将会影响整个系统可靠运行.

根据上文所述主要故障原因对MEMS安全系统构建故障树，如图2所示，其中各基本事件如表1所示.

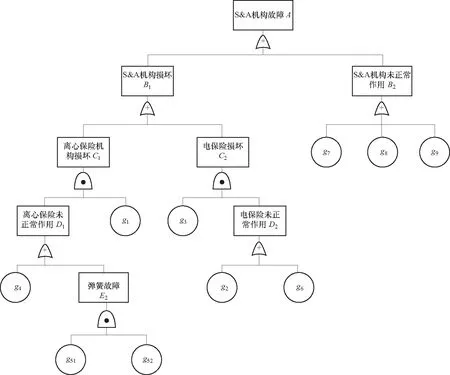
图2 MEMS安全系统的故障树Fig.2 Fault tree of MEMS S&A device

表1 故障树基本事件定义Tab.1 Definition of basic events of fault tree

2 可靠度建模计算

2.1 可靠度功能函数的建立

功能函数主要依据导致失效的失效判据建立. 在MEMS安全系统中，其失效主要由断裂、屈服失效产生. 结构可靠度的获取，是用于评价结构设计是否满足指标要求. 依据概率理论，假设随机变量x的联合概率密度函数为fx(x)，概率模型可转化为如式(1)所示的积分形式

(1)

可以发现，结构失效概率和结构可靠度分别等于fx(x)在失效域g(x)<0和安全域g(x)>0内的积分.

2.2 安全系统可靠性功能函数分析

对安全系统结构进行简化，根据故障树建立每个部件的可靠性功能函数. 闭锁机构简化为悬臂梁结构，结合MEMS安全系统的作用过程，可以确定该结构量化的设计要求，并通过理论分析确定各设计要求的满足情况，当MEMS安全系统受离心力时，隔爆滑块与闭锁簧片之间的位置关系以及相关的受力关系如图3 所示.

由图3可以计算出隔爆滑块只受离心力时的计算公式

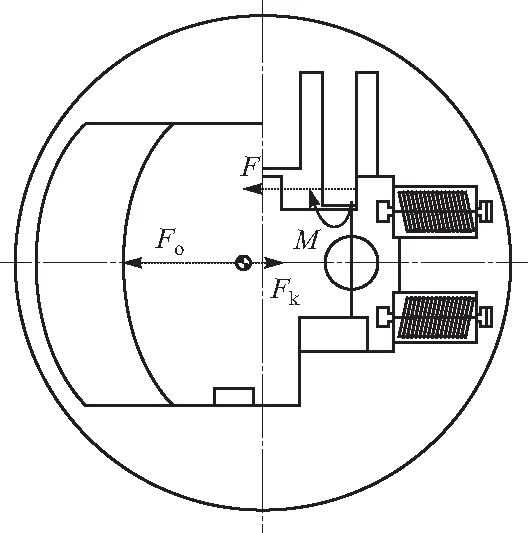
图3 爆滑块与闭锁簧片的位置关系及受力分析Fig.3 Positional relationship and force analysis of explosion-proof slider and locking reed

(2)

式中：ms为滑块质量；rs为滑块的偏心距；n为弹药的转速.

同时，Fa会在滑块与闭锁簧片接触位置产生一个等效弯矩M.

应用材料力学悬臂梁的挠曲线方程对隔爆滑块与闭锁簧片之间的受力关系进行分析，如图4所示，可以得到闭锁簧片挠度W的计算公式

图4 闭锁簧片挠度分析示意图Fig.4 Schematic diagram of deflection analysis of locking reed

(3)

式中：A=L且L为闭锁簧片的长度；E为闭锁簧片材料的弹性模量；I为闭锁簧片材料的截面惯矩. 因此，闭锁簧片在同时受力和力矩作用时，等效到仅施加闭锁簧片上的等效力F′为

(4)

结合式(2)可得

(5)

式中e0为2个力之间偏移的距离. 根据悬臂梁结构的受力分析可知，闭锁簧片可等效为纯弯曲受力情况，而且闭锁簧片所受的最大弯曲应力σ发生在其根部

(6)

式中H和B0分别为闭锁簧片的厚度和宽度. 根据设计要求，MEMS安全系统在最大离心转速(75 000 r/min)作用下，闭锁簧片不发生屈服失效，其中闭锁簧片材料的屈服极限为σs=1 200 MPa，因此可得到隔爆滑块闭锁簧片的强度失效机理模型g1

(7)

式中：ρ，ss和H1分别为滑块的材料密度、表面积和厚度，另外，滑块，闭锁簧片以及离心保险机构所用材料相同，以下均用ρ表示.

当MEMS安全系统的闭锁簧片受电推冲器的作用时，电推冲器及闭锁簧片的位置关系及其结构参数如图5所示.

图5 电推冲器及闭锁簧片的位置关系及其结构参数Fig.5 Position relationship and structure parameters of electric thruster and locking reed

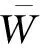
(8)

式中根据设计要求，闭锁簧片在受后坐力(acc=600 000 m/s)的作用下，闭锁簧片的变形量需要小于0.6 mm，因此可得到闭锁簧片在后坐力作用下的位移失效机理模型g3

(9)

在弹丸发射出炮口前，旋转速度达到40 000 r/min-1时，需要解除离心保险. 其中，MEMS安全系统的离心保险机构如图6所示，其中，较长且截面较细的梁结构等效为弹性元件，头部截面较宽的结构等效为质量块. 结构设计要求为：弹丸转速40 000 r/min-1时，离心保险机构的变形量(远离旋转中心)不小于0.7 mm，实现离心保险的解除.

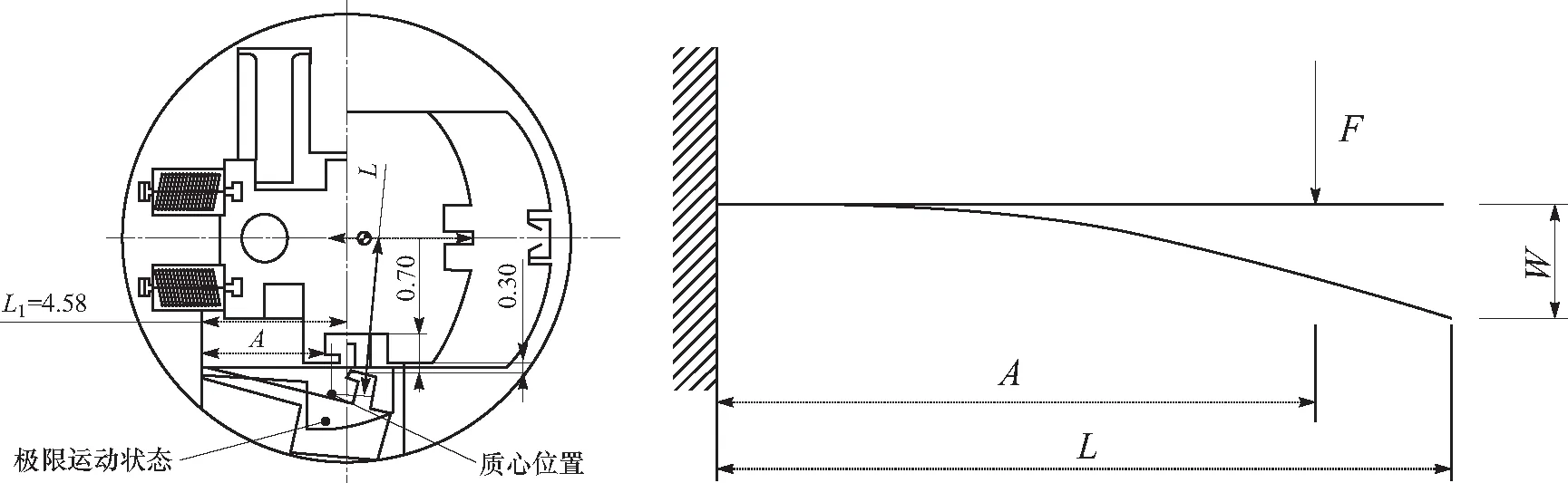
图6 离心保险机构的结构设计参数Fig.6 Structural design parameters of centrifugal insurance mechanism

针对离心保险机构的结构分析，离心保险机构可以等效为悬臂梁结构，因此可以得到离心保险机构的挠度WL计算公式如下

(10)

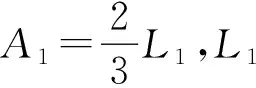
(11)

MEMS弹簧结构布局及其结构参数示意图如图7所示，结合MEMS安全保险装置的作用过程，可以确定该MEMS弹簧的量化设计要求，并通过理论分析确定各设计要求的满足情况，在引信作用过程中，离心保险和电火工保险均处于解保状态下，MEMS弹簧受滑块拉力作用下变形量不少于2.2 mm，以确保闭锁机构能够到达闭锁位置有效闭锁.

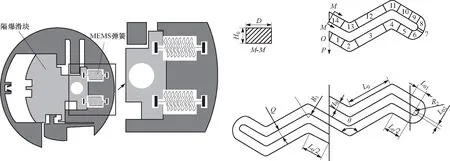
图7 MEMS弹簧结构布局及其结构参数Fig.7 MEMS spring structure layout and its structural parameters

当滑块开始运动时，当运动距离为x时，隔爆滑块所受的合力Fm大小为离心力与弹簧拉力的合力，其表达式如下

(12)

滑块所受的离心力与弹簧的拉力都是在逐渐增大的过程，因为弹簧的拉力是从0开始增大的，所以在滑块的运动过程中Fm在达到0之前一直是>0的，因此取Fm=0的情况，可求得滑块的最大行程

(13)

式中：n为电保险解保后、闭锁机构闭锁时对应的弹丸转速，为弹丸最大转速的80%，取60 000 r/min；k为MEMS弹簧的弹性系数.

因此，根据设计要求，可得到在离心力的作用下，弹簧在受滑块拉力时位移的失效机理模型. 由于两弹簧完全相同，因此失效机理模型均用g5表示

(14)

蒙特卡洛法是根据功能函数中的随机向量，首先产生一系列随机数x1，x2，…，xN，然后计算相应的功能函数值，各功能函数gi(x)所考虑的随机变量分布类型为正态分布，经过蒙特卡洛模拟计算可得各机构的可靠度如表2. 其中电推冲器故障，离心力过小，发射时后坐力不足，勤务过程中发生损坏概率均根据GJBZ 179-2015引信故障树底事件数据手册所得.

表2 失效模式可靠度结果Tab.2 Reliability results of each failure mode

3 安全系统BN模型建立

3.1 FTA与BN之间的转化

贝叶斯网络(Bayesian network, BN)融合了图论、概率论和信息论等理论基础，引入了连接边和条件概率，用来表达数据变量之间的依赖关系[7]. BN表示一个有向无环图G=(V,E,θ)，其中结点集合V={X1,X2,…,Xn}表示变量，有向边集合E表示变量间的直接依赖关系，模型参数θ表示结点各状态间的条件概率，即对于每一个结点Xi∈V都有一个条件分布族P(XI|pa(Xi))，其中pa(Xi)为父结点集合. 将联合概率分布表示为

(15)

BN充分利用了专家先验知识，引入条件独立性假设条件，简化了信息的获取和模型的构建，为人们提供了一种将知识直觉地可视化的方法，逐渐成为不确定性问题知识表示和推理的主流技术[8].

FTA向BN的转化过程主要包括图形转化以及数值转化[9]，图形转化是将FTA中的各级事件用相应的BN节点表示，逻辑符号由具体的条件概率代替；数值转化是将基本事件的状态概率作为BN中根节点的先验概率. 图2所示安全系统FTA转化为图8所示的BN网络，各节点字母与图2所示相同，转换过程中的逻辑关系如图9所示.

图8 FTA转化为BN图Fig.8 FTA converted to BN diagram

图9 FTA转化BN图逻辑关系Fig.9 FTA transformation BN diagram logical relationship

本文利用GeNle软件构建BN模型，该软件通过联合树算法计算出不同结构BN模型的可靠度. 将各基本的事件的可靠度以及各事件的先验概率带入，可以求得本文中的MEMS引信安全系统可靠性为0. 999 656.

3.2 复杂系统的重要度计算

基本事件的重要度主要包括结构重要度、概率重要度及关键重要度3个内容[10]. 概率重要度的物理意义是当且仅当元件xi失效时系统处在某一失效状态下的概率. 它反映了根节点xi所有故障状态对叶节点T故障状态为TC的影响程度[11]. 本文只考虑每个节点发生故障与正常工作2种状态，故基于前文论述，概率重要度可由如下式子进行计算

(16)

结构概率为不考虑根节点发生的概率，结构重要度仅从贝叶斯网络结构上分析各个根节点的发生对叶节点发生的影响程度[12]. 基于前文的论述，本文只考虑节点的失效与正常作用2种故障状态，每个根节点的4种状态的概率都为1/2.

(17)

根据前文BN网络先验概率以及各节点后验概率，求得各基本事件的重要度如图10所示.

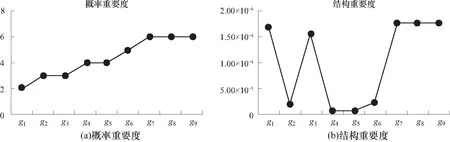
图10 节点事件概率重要度及结构重要度Fig.10 Probability importance and structural importance of each node

图10中y轴为各节点的重要度，x轴表示故障树中各个根节点. 其中，代表发射环境不满足设计的两种情况，即离心力过小，发射时后坐力不足以及勤务过程中发生损坏，在概率重要度中还是结构重要度中均为最高值，这代表了目前大多数MEMS安全系统的失效是由于发射环境所导致的，在发射环境不满足设计条件时，即使不存在设计缺陷，MEMS安全系统发生失效可能性也是更大，设计中的薄弱环节是影响MEMS安全系统可靠性的因素，不是最主要因素，但作为设计者仍需在设计中不断优化，提高整体可靠性. 在MEMS安全系统设计方面，从概率重要度上，离心保险机构无法完成预定功能和弹簧不能满足变形量要求对顶事件影响更大，离心保险机构功能函数计算结果可知其可靠性较高，但在设计中仍需要加强相关设计；闭锁簧片在离心力作用下屈服失效及闭锁簧片在后坐力作用下的变形失效在结构重要度上均占据重要位置，从定性角度分析可认为闭锁簧片失效对整个MEMS安全系统是可靠性影响极大，由功能函数可知其有一定失效可能，因此后续可对闭锁簧片进行优化设计.

4 加工及试验验证

该MEMS安全保险装置所用的MEMS弹簧采用UV-LIGA工艺进行加工；其他零件采用慢走丝电火花线切割工艺及精密冲压工艺进行加工. 根据MEMS安全系统的设计准则和系统可靠性的要求，设定如下试验方案. 分别施加60 000 g和65 000 g冲击加速度，持续时间 50 μs，以验证跨尺度安全系统的闭锁簧片是否存在明显变形. 结果如图11所示，闭锁簧片在60 000 g和65 000 g的后坐冲击力下均未出现明显变形或破坏情况. 施加以 25 000 r/min为初始值，40 000 r/min为截止值， 1 000 r/min为步长的离心转速，并分别持续时间20 s，验证闭锁簧片处于闭锁状态时，离心保险机构是否正常解除保险. 如图12所示，当施加 36 000 r/min-1的转速时，离心保险机构完全解除保险.

图11 闭锁簧片的冲击试验Fig.11 Impact test of locking reed

图12 离心保险解除状态微观图Fig.12 Microscopic view of the release state

分别施加60 000，65 000，75 000 r/min离心转速，持续时间20 s，验证闭锁簧片处于闭锁状态、离心保险处于解除状态时，闭锁簧片是否发生屈服失效或存在明显变形以及闭锁簧片与离心保险均处于解锁状态时隔爆滑块是否运动到位. 试验结果表明，闭锁簧片在离心转速达65 000 r/min-1时，会存在屈服失效问题，是系统的薄弱环节，与功能函数计算结果相吻合. 所有试样的隔爆滑块均可以运动到预定位置，传爆孔对正，弹簧的变形量满足要求. 如图13所示，此时弹簧发生了屈服失效，但并未影响到安全系统的功能，因此可以认为弹簧不是系统的薄弱环节.

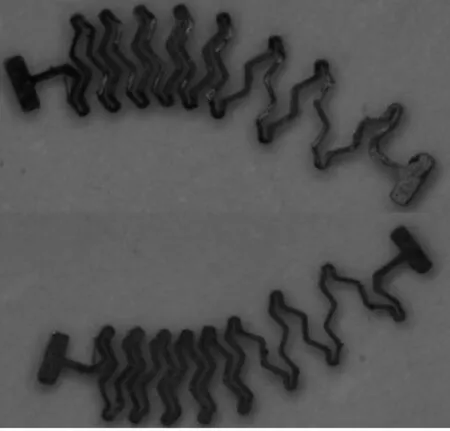
图13 MEMS弹簧变形情况的微观图Fig.13 Microscopic view of MEMS spring deformation

对MEMS弹簧分别施加 60，80，100，120，140 N 拉力，持续时间均为5 s，分析闭锁簧片受电推冲器作用的变形情况. 对实验结果进行总结可知，当施加 100 N 拉力时，闭锁簧片的变形量均大于 0.75 mm；如图14所示，施加 140 N 拉力时，闭锁簧片变形量均大于1 mm. 试验结果表明，闭锁簧片受力与变形基本满足线性关系，拉力大于100 N 时，能满足闭锁簧片解除保险的要求.

图14 拉伸试验结果Fig.14 Tensile test result

5 结 论

本文分析了某MEMS引信安全系统的机构，构建了该安全系统的故障树模型，并详细分析了各重要部件的功能函数，通过蒙特卡洛模拟得到了各功能函数的可靠度. 将FTA转化为BN网络，并利用GeNle软件画出BN网络，经联合树算法计算出整个安全系统的可靠性. 在对不同的功能函数进行概率重要度和结构重要度分析，可知在设计上提高MEMS弹簧和离心保险机构的可靠性能够提高整个安全系统的可靠性. 加工MEMS安全系统后，进行了可靠性试验，证明了BN网络可以有效计算MEMS安全系统的可靠性.