基于有限元分析的永磁同步电机实时模拟器研究

王志福，孙庆乐，李昊龙，王军，沈宏继 (.北京理工大学 机械与车辆学院，北京 0008；.广西科技大学 电气与信息工程学院，广西,柳州 54506； .中国人民解放军696部队，北京 0007)

永磁同步电机(permanent magnet sychronous motor,PMSM)由于效率高、体积小、功率密度大等优点在电动汽车电驱动系统中得到越来越广泛的应用[1]. 永磁同步电机的广泛应用带动了电驱动系统的快速发展，并对电驱动系统的测试提出了更高的要求. 功率硬件在环(power hardware in loop,PHIL)测试作为一种新兴的测试技术，通过数字仿真和电力电子器件来模拟真实电机的端口特性，能够大大缩短电驱动系统的测试周期，降低研发成本，节能环保，受到了广泛的关注[2].

目前，PHIL测试技术已广泛用于模拟三相感应电机[3-4]、永磁同步电机[5-6]、开关磁阻电机等[7]电机的特性，研究重点主要集中在实时电机模型、系统拓扑结构及接口控制算法上. Alvarez等[8]基于d-q坐标系提出了PMSM电流-磁链有限元反查表模型，但其在坐标变换过程中进行了简化假设，降低了模型精度.

PHIL系统拓扑结构主要指功率级结构. Masadeh等[9]采用三相两电平电压源逆变器设计了三相感应电机模拟器，其结构简单、调制方便，但模拟精度需通过精确的控制实现. Schmitt等[6]针对PMSM采用模块化多相多电平逆变器设计了PHIL测试系统，提高了模拟精度及动态特性，但也带来了调制难度大、系统可靠性低等问题.

本文针对三相PMSM设计了一种PHIL实时模拟器结构. 为提高电机的模拟精度，提出了一种基于三相定子坐标系的电流-磁链有限元反查表模型. 为解决电流环控制冲突问题，提出了电压前馈电流反馈控制的接口算法，并针对电流反馈环节提出了一种模糊PI控制算法. 最后，通过联合仿真实验测试方法对接口控制算法和电机模拟器进行了测试与对比分析，验证了其有效性.

1 电机模拟器系统概述

所提出的三相PMSM实时模拟器系统拓扑结构如图1所示. 其中MCU为电机控制器，用于运行电机控制策略并输出驱动电压与电流；PHIL模拟器为功率硬件在环实时电机模拟器，用于模拟电机的电流(转矩)、转速等特性；左右两侧电源均为直流电源，可实现电能的供给与吸收.

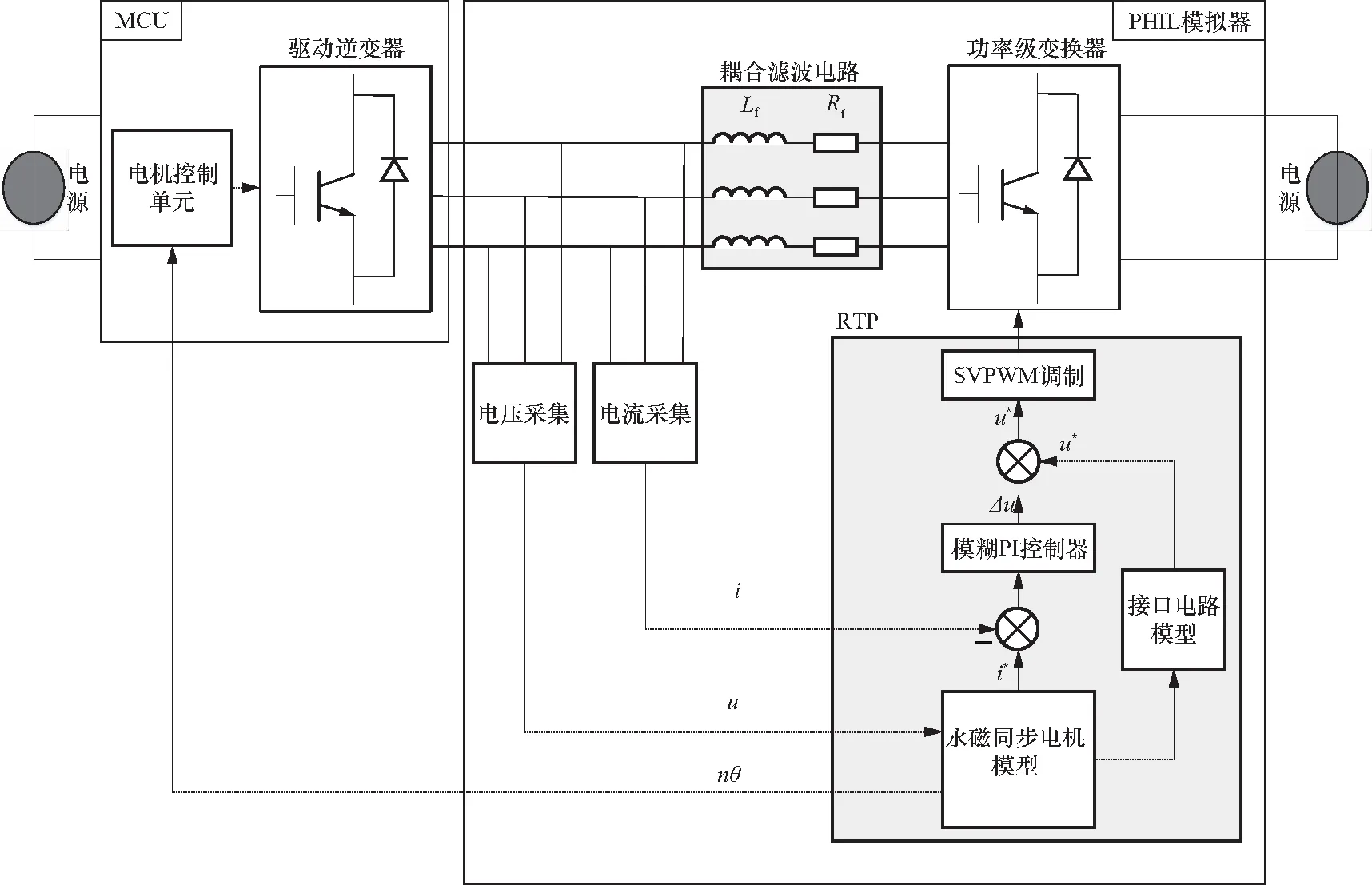
图1 电机模拟器系统拓扑结构Fig.1 Topology structure of the motor emulator system

实时处理器(RTP)作为PHIL模拟器控制的核心，运行给定的电机模型、接口控制算法及PWM调制算法，实时控制功率级变换器输出的电压与电流. 因此，RTP要求高实时性. 由于FPGA芯片能够并行处理数据，执行速率可达MHz级别. 因此，此处RTP采用FPGA芯片，运行时间小于1 μs.

功率级变换器作为实时功率交互的核心组件，其必须能够实现对RTP输出的参考电压或电流信号的精确快速跟踪才能保证PHIL模拟器的精度，因此，其采用三相两电平电压源型IGBT变换器.

耦合滤波电路作为MCU与功率级变换器之间的缓冲滤波网络，其一方面可以避免两电压源型变换器直接并联而导致的电流不均衡问题，另一方面可以实现对三相电流的滤波，提高模拟精度. 目前，耦合滤波电路主要有L型、LC型及LCL型，由于LC型及LCL型容易造成系统振荡，并且控制复杂，因此，本文采用L型电路开展设计.

PHIL模拟器的工作过程为：首先，电压采集电路对MCU输出的三相电压进行采集，并将采集信息发送至RTP，RTP通过给定的电机模型及接口电路模型计算功率级变换器侧的期望电压与电流. 随后，为实现对电机期望电流值的精确跟踪，引入电流负反馈与期望电流进行比较并通过模糊PI控制器产生调整电压，与期望电压叠加后得到最终输出电压，并经SVPWM调制对功率级逆变器进行精确控制. 同时，RTP通过电机模型将电机转速、转角等信息实时反馈回MCU.

2 电机及接口电路模型

2.1 永磁同步电机模型

三相定子坐标系下PMSM电压方程为

(1)

式中：

uabc、iabc、ψabc分别为电机的三相电压、三相电流和三相磁链；Rs为电机相电阻.

三相磁链通常为相电流iabc和转子位置角θ的函数，考虑到三相电流之和为0，故其方程为

(2)

在PHIL测试中，电机模型以三相电压作为输入，以三相电流作为输出. 但方程(1)通过积分运算仅提供了三相磁链，故输出电流需通过方程(2)的逆运算得到，其方程为

(3)

由于方程(2)的高度非线性，难以对其实现实时的逆运算. 为建立实时的电机模型，利用有限元软件计算方程(2)的映射关系，在此基础上，通过离线运算建立电流-磁链三维反查表模型，具体实现过程见第2.2部分.

电机电磁转矩方程亦采用有限元查表模型，其方程为

Te=h(ia,ib,θ)

(4)

此外，电机运动方程为

(5)

式中:TL为电机负载转矩；J为转子转动惯量；B为转动阻尼系数；ωm为机械角速度.

所提出的PMSM模型计算过程如图2所示. 该模型考虑了磁饱和、齿槽效应及空间谐波等因素的影响，避免了坐标变换，提高了模型精度，并能够满足实时性高的要求.

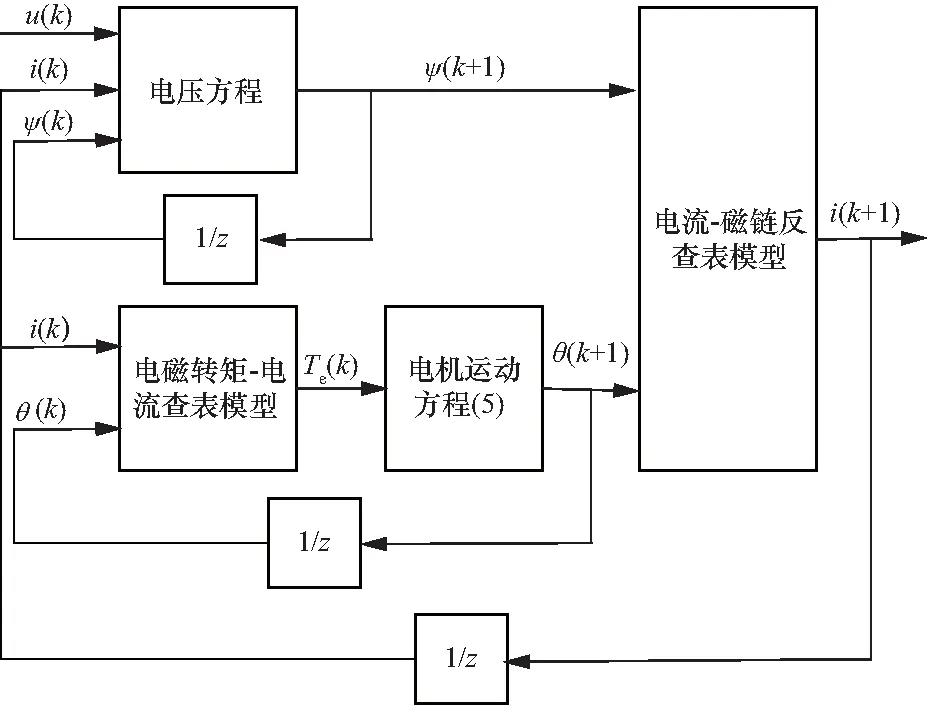
图2 电机模型计算过程示意图Fig.2 Schematic of the calculation process of the motor model

2.2 有限元模型

为得到上述查表模型，利用电磁场有限元分析软件JMAG建立了三相8极48槽PMSM的有限元分析模型，如图3所示.

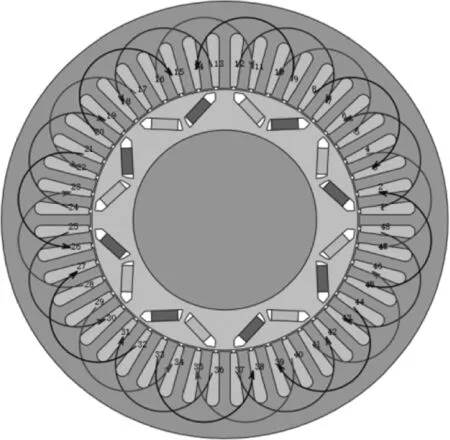
图3 PMSM有限元分析模型Fig.3 Finite element analysis model of PMSM

考虑到该模型的对称性，本文采用1/8模型进行有限元分析，并对其进行材料定义、网格划分与边界条件设置.

在电磁场求解设置中，定义相电流幅值、相位及转子位置角为参数化分析对象，其范围分别为[0，240 A]、[0，360°]、[0，90°]，步长分别为20 A、15°、3°，可得到在不同转子位置角下，磁链、转矩与相电流幅值和相位的映射关系. 设定电机ia、ib的求解范围均为[-240 A，240 A]，求解步长均为12 A，利用ia、ib与相电流幅值Im和相位φ间的关系：

(6)

可得到不同的(ia，ib)所对应的(Im，φ)，从而得到不同转子位置角下的磁链-电流及转矩-电流三维查表模型. 在转子位置角θ=0时，磁链-电流查表模型如图4和图5所示.

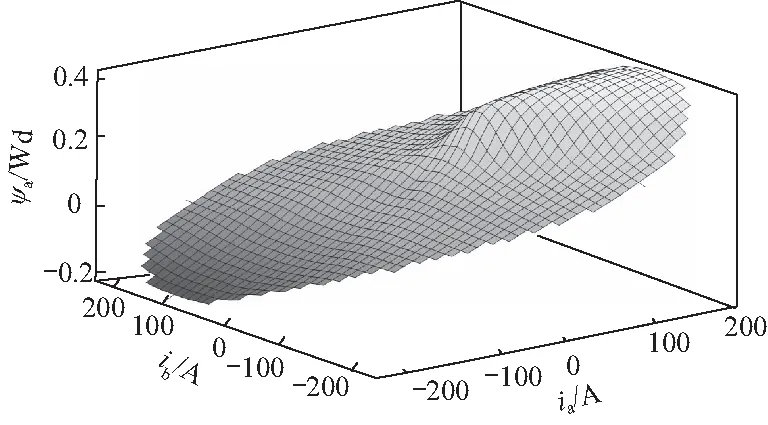
图4 相磁链-电流查表模型Fig.4 Flux-current look-up table model of phase a

由图4和图5可知，对于给定的转子位置角，磁链-电流间的映射关系存在单调性. 因此，对于给定的(Ψa，Ψb)可确定唯一的(ia，ib)，从而为电流-磁链反查表模型的建立提供了条件. 基于此条件，利用

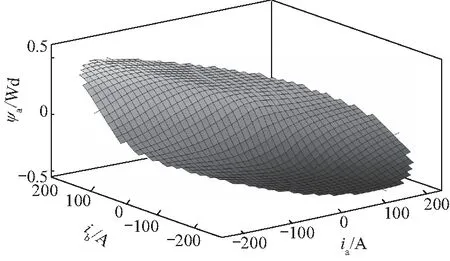
图5 b相磁链-电流查表模型Fig.5 Flux-current look-up table model of phase b

上述所得到的磁链-电流查表数据，可直接得到电流-磁链的反向映射关系，对该映射关系在不同转子位置角下进行曲面拟合和(Ψa,Ψb)插值，可得到电流-磁链反查表模型. 在转子位置角θ=0时，相应的反查表模型如图6和图7所示.

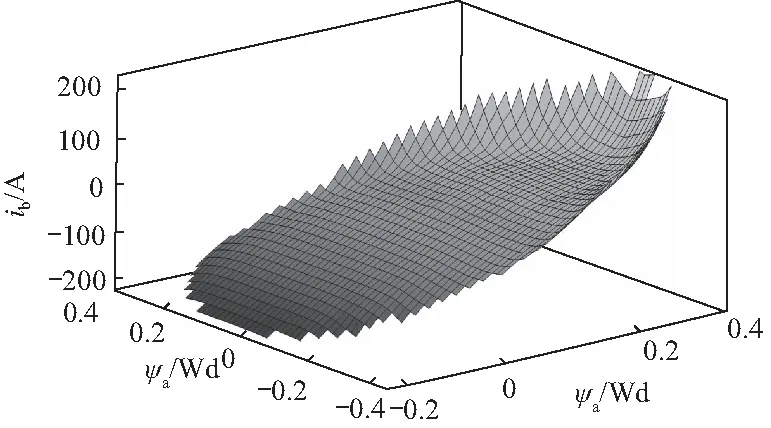
图6 相电流-磁链反查表模型Fig.6 Current-flux reverse look-up table model of phase a

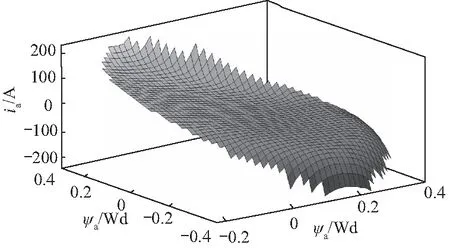
图7 相电流-磁链反查表模型Fig.7 Current-flux reverse look-up table model of phase b

2.3 接口电路模型

PHIL模拟器为实现对期望电流值的跟踪，需精确控制电机模拟器侧功率级变换器的输出电压，为此建立了接口电路的等效模型，如图8所示.

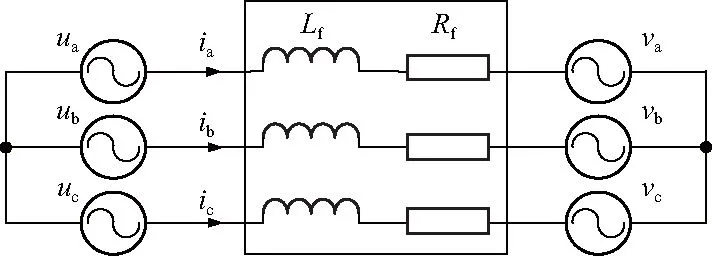
图8 接口电路模型Fig.8 Model of the interface circuit

由图8可建立三相静止坐标系下的接口电路电压方程为

(7)

式中:vabc为功率级变换器的三相输出电压；Rf、Lf分别为耦合滤波电路的电阻和电感.

对方程(7)进行Clark变换和Park变换，可得到d-q坐标系下的电压方程为

(8)

式中:ud、uq分别为MCU侧三相电压的d、q轴分量；id、iq分别为MCU侧三相电流的d、q轴分量；vd、vq分别为功率级变换器侧三相电压的d、q轴分量；ωe为电角速度.

3 电机模拟器系统设计

3.1 接口控制算法设计

PHIL模拟器必须针对接口电路设计合理的控制算法，以实现对期望电流值的精确跟踪. 由于MCU一般采用电流环控制，若PHIL模拟器亦采用电流环控制，则将引起控制冲突，使系统产生振荡，降低系统稳定性. 本文提出一种电压前馈电流反馈控制的接口算法，如图1所示. 其一方面可以避免电流环控制引起的控制冲突，另一方面由于电压前馈可以提高系统动态响应速度，电流反馈可以提高系统跟踪精度，因而可以使系统同时达到高速性和高精度的目标.

由方程(8)，得到前馈环节的电压方程为

(9)

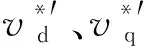
对于电流反馈环节的设计，由于控制过程存在的非线性、参数时变特性，因此，采用常规PI控制无法实现对接口电路的精确控制及对电机电流的精确模拟. 基于此，提出了一种模糊PI控制算法，根据电流反馈误差对前馈环节得到的d-q轴电压进行实时调整，从而得到最终输出电压为

(10)

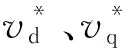
3.2 常规PI控制的参数整定

为实现电流反馈环节模糊PI控制器的设计，首先需要进行常规PI控制参数的设计整定. 本文以PHIL模拟器对期望直轴电流值的模拟跟踪为例进行分析. 将功率级变换器建模为具有增益G及时间常数Td的一阶惯性环节，其中Td为PWM周期的1/2，从而得到PHIL模拟器侧直轴电流模拟控制的系统框图如图9所示. 图中，Kfi和Tfi分别为电流传感器的增益和时间常数；Tf为耦合滤波电路的电气时间常数，Tf=Lf/Rf；Kpd和Kid分别为PI控制器的比例和积分增益，Tid=Kpd/Kid.

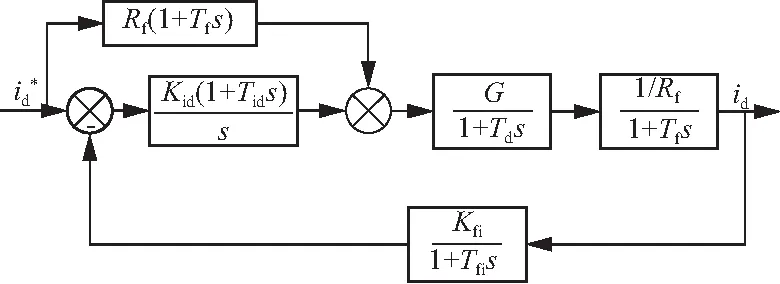
图9 直轴电流模拟控制框图Fig.9 Block diagram of d-axis current emulation control

由于耦合电路的时间常数Tf远大于系统中的其他环节，因此电压前馈电流反馈环节的零点设计为消除耦合电路引入的极点，以提高模拟带宽. 对图9所示系统进行传递函数推导可知，此时满足以下条件

Tid=Tf

(11)

另外，由于TdTfi很小，在进行传递函数简化时可忽略. 因此，系统闭环传递函数为

对于该二阶系统，可知其阻尼比ξ和固有频率ωn满足下式：

(13)

当阻尼比为ξ= 0.707时，该二阶系统可获得最优的响应特性. 因此，常规PI控制的积分增益为

(14)

3.3 模糊控制规则的建立

所提出的模糊PI控制算法，以交直轴电流的模拟误差e及其变化率ec为输入，利用模糊控制理论，通过模糊推理实现对上述常规PI控制参数的实时整定，模糊PI控制结构如图10所示.

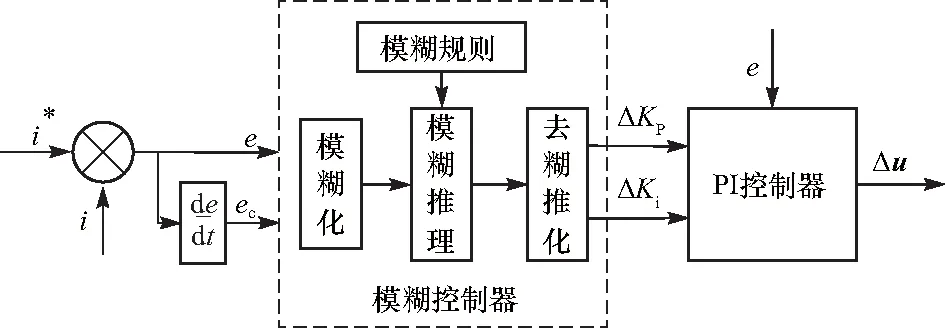
图10 模糊PI控制结构Fig.10 Structure of fuzzy PI control

模糊规则是进行模糊推理的核心，所建立的模糊规则如表1和表2所示.

表1 比例增益Kp的模糊规则表

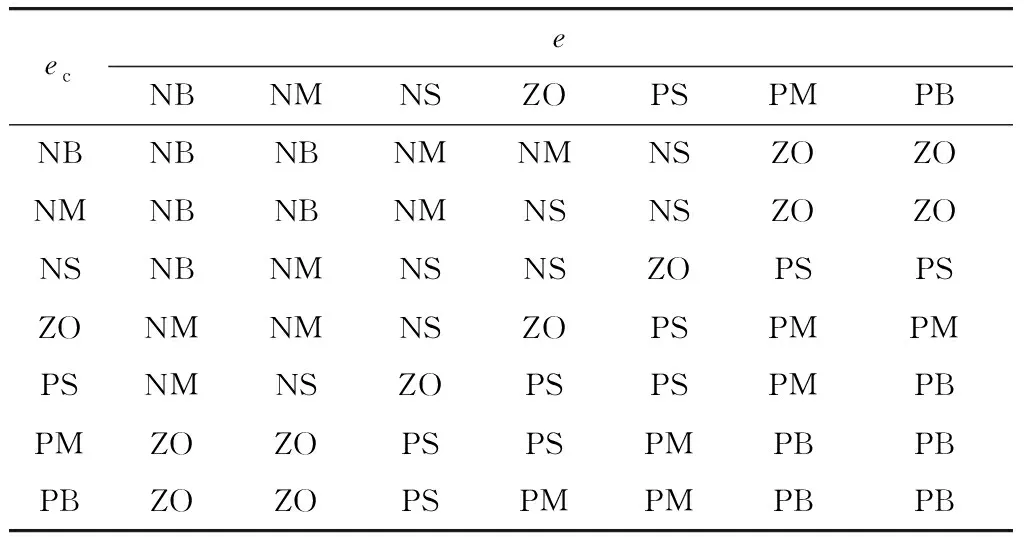
表2 积分增益Ki的模糊规则表

模糊推理方法采用极值法，解模糊方法采用重心法，可得到比例增益调整量ΔKp和积分增益调整量ΔKi的精确输出值. 因此，可得到最终的控制参数为

(15)

3.4 耦合滤波电路的设计

由图9可知，当耦合电路电阻值不变时，随着电感值的增加，系统的模拟带宽减小，动态特性恶化；随着电感值的减小，电路滤波能力下降，电流纹波增加. 因此，理想的电感值应尽可能接近电机的平均电感[5]. 对于PMSM，耦合滤波电路的电感值设计为

(16)

式中Ld、Lq分别为定子d、q轴的平均电感，可通过JMAG-RT软件直接计算得到.

文献[10]指出，实际电机系统的响应时间受电气时间常数的限制. 因此，在实际测试中，为保证PHIL测试系统的精度，耦合电路的电气时间常数必须小于电机的电气时间常数，考虑到系统其他因素的影响，耦合电路的电气时间常数选择为

(17)

因此，耦合滤波电路电阻值的大小为

Rf=Lf/Tf

(18)

4 仿真分析

为验证接口控制算法和电机模拟器的有效性，通过Matlab/Simulink及其与JMAG-RT的联合仿真对其进行了测试与对比分析. MCU采用id=0的矢量控制算法，电机及PHIL系统参数如表3所示.

表3 PMSM电机参数

4.1 接口控制算法验证测试

为验证接口控制算法的有效性，应避免MCU中电流闭环控制所产生的补偿作用，因此，MCU采用电流开环控制. 当转速指令为1 000 r/min，并在0.2 s时施加阶跃负载转矩指令50 N·m时，PHIL测试系统仿真结果如图11所示，图中以RTP中电机模型的计算输出量作为各参数的期望值.

由图11(a)可知，MCU采用电流开环控制时，系统仍能保持稳定，但转速动态响应特性恶化. 同时，稳态时直轴电流与期望零值会产生偏差，如图11(b)所示.

由图11(b)(c)可知，所提出的接口控制算法对电机模型输出的期望交直轴电流均能实现较好的模拟跟踪. 由于相电流模拟跟踪效果是交直轴电流综合作用的结果，因此相电流亦能够实现对期望值快速而精确地跟踪，其在额定工况下的稳态相对误差小于2%，如图11(d)(e)所示. 同时可发现，即使在瞬态过程中a相电流误差仍保持在较低水平(小于5%)，这是由于加入了电压前馈环节，提高了动态响应速度. 造成电流跟踪误差的主要原因在于电压与电流传感器的滤波效果及逆变器的死区时间.

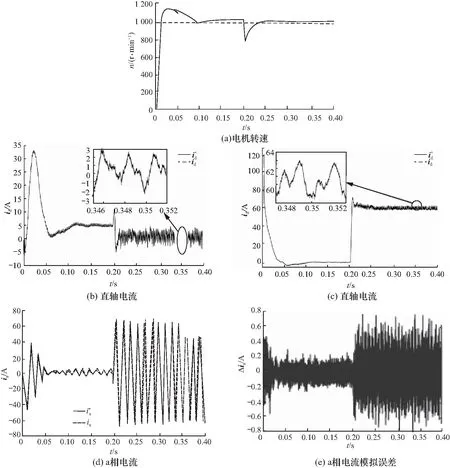
图11 接口算法验证测试Fig.11 Verification test of the interface algorithm

4.2 电机模拟器系统验证测试

为验证电机模拟器的有效性，对PHIL测试系统进行了仿真分析，并与Matlab/Simulink和JMAG-RT联合仿真下的机械式测试系统进行了对比. 试验条件为：转速指令为1 000 r/min，在0.1 s时施加阶跃负载转矩指令50 N·m. 仿真结果如图12所示，图中以联合仿真的结果作为各参数的期望值.

由图12(a)(b)可知，电机模拟器的输出转速能够较好地跟踪电机期望转速，其相对误差在瞬态时小于1%，在稳态时小于1‰. 另外，与图11(a)对比可知，由于此时MCU采用电流闭环控制，因此转速响应速度较快.

图12 PHIL测试系统仿真结果Fig.12 Simulation results of PHIL test system

由图12(c)(d)可知，电机模拟器在瞬态及稳态工况下均能实现对期望交直轴电流快速而精确地模拟跟踪，瞬态过程中交直轴电流的误差虽有所增加，但仍处于较低水平.

由图12(e)(f)可知，电机模拟器相电流能够快速而精确地跟踪期望值，这是交直轴电流综合作用的结果. 瞬态过程中电流误差虽有所增加，但其相对误差小于5%. 同时可看到，额定工况下随着电流幅值的增加，稳态误差呈现出与电流频率相同的正弦交流信号，其值虽有所增加，但相对误差小于3%.

5 结 论

本文针对三相PMSM设计了一种PHIL实时模拟器结构. 为了提高电机的模拟精度，提出了一种基于三相定子坐标系的电流-磁链有限元反查表模型. 为了解决电流环控制冲突问题，提出了电压前馈电流反馈控制的接口算法，并针对电流反馈控制环节提出了一种模糊PI控制算法. 最后，通过Matlab/Simulink及其与JAMG-RT的联合仿真实验测试方法对接口控制算法和电机模拟器进行了测试与对比分析，验证了其有效性.