卡尔曼滤波融合遗传PID控制算法在提高播种精度中的应用

2021-10-14马利强陈雪辉俞传阳

安徽农业大学学报 2021年4期

刘伟，马彪，马利强，陈雪辉，俞传阳，黄磊，李昊

(安徽建筑大学机械与电气工程学院，合肥 230601)

精密播种作为一种先进的现代化农作物种植技术，通过控制播种量精度、株间距精确度及播种深度的精确度来实现减少种子投放量、提高出苗率和增加农作物产量的目标[1]，播种器作为实现精密播种的一个重要器件，其结构形式和驱动方式直接影响到播种质量的好坏。采用地轮驱动的播种器，由于受到复杂地势的影响很容易发生地轮打滑和传动机构卡死的现象，造成漏播以及种间距不均匀的现象[1]，直接影响农作物的产量；采用电机驱动的播种器，利用内外气压差将种子吸附在播种盘上，解决了因地轮打滑造成漏播影响农作物产量的问题[2]，但播种质量会受到播种盘转速、真空压力大小以及导种管形式等因素的影响[3]。播种盘转速过高时，种子离心惯性力大，若气压不足便会导致漏吸，造成播种精度下降；当播种盘转速过低时，部分吸孔会重复吸种，重播率增大，造成种子的浪费。由此可见，要实现精密播种就需对播种器驱动电机的转速进行精密的控制。

PID控制因其算法简单和鲁棒性好，被广泛应用于各种工业过程控制，但当控制系统中存在控制干扰信号和测量噪声时，控制系统会产生系统精度差，响应时间长，稳定性不高等缺陷，导致控制系统达不到理想的控制精度。为解决PID控制存在的缺陷，赵红等[4]和王婷婷等[5]把模糊控制器与PID控制器相结合，设计了一套基于模糊控制的PID控制算法，通过对模糊控制器隶属度函数进行优化，提高了PID控制器的响应时间和抗干扰能力；杨柳曼等[6]、赵连娟等[7]和徐会风等[8]把卡尔曼滤波与PID控制相结合，通过对比PID控制和基于卡尔曼滤波的PID控制两种控制方式的控制效果，论证了卡尔曼滤波在消除控制干扰和测量噪声影响上有着显著的效果。采用试凑法选取Kp、Ki和Kd不仅会花费大量的时间，而且还很难选取到最佳的取值，朱静涛等[9]、Mousakazemi等[10]、张震等[11]、曹莹等[12]和吴晓莉等[13]在PID参数整定中引入了遗传算法，通过将PID控制的Kp、Ki和Kd设定为不同的目标函数，快速高效的得到其最优的取值。

针对现代化农业精密播种要求，本研究设计了一种基于卡尔曼滤波的遗传PID控制算法用于提高播种器的播种质量，该套算法通过卡尔曼滤波将外界干扰信号对播种盘转速影响最小化，再通过遗传算法选择出最优的PID参数，最后对播种盘电机的数学模型进行仿真，通过对比仿真结果验证了所设计的控制算法在改善播种器播种质量中的有效性。

1 播种器模型建立

1.1 播种器结构

气吸式播种盘的主要的结构由上壳体、下壳体、种盒、清种刀、排种盘、负压气管、挡种毛刷、驱动电机和型孔等组成[9,14-15]，其结构示意图如图1所示。

图1 播种器整体结构示意图Figure 1 Overall structure diagram of seeder

播种器在进行工作时，气吸室中的气流使得播种盘两侧产生压力差，利用产生的压力差将种子吸附在播种盘上面，被吸附的种子随着播种盘一起转动，脱离了种群的束缚，完成了与种群分离的过程；接着被吸附的种子随着播种盘进入清种区，在清种刀和挡种毛刷的作用下，将型孔周围的多余的种子清除掉，仅留下单粒种子；清种完成后，留下的种子进入落种区，落种区内的气压被阻断，种子便从型孔上脱落下来，进入导种管完成播种[3-6]。

1.2 播种盘数学模型建立

为研究播种盘转速对播种质量的影响，以气吸式玉米播种机为例进行模型的建立。根据《谷物播种机技术条件》[16]可知，当同一排种轴上的排种器数量小于等于12时，排种轴的阻力距不大于10 N·m；玉米播种的种间距一般为25～33 cm，本次选择种间距s为30 cm，排种盘的吸孔数z为25，减速器的减速比i为40∶1；拖拉机正常的作业速度v为5～10 km·h-1，根据土壤含水率等因素本次选择的拖拉机作业速度为7 km·h-1。

根据上述参数可得驱动电机的转速[3-4]N为：

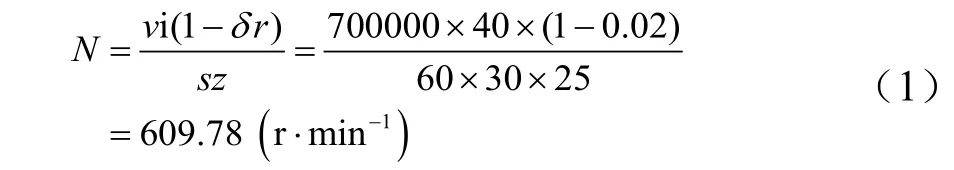
其中v为拖拉机的作业速度，δr=2%为拖拉机的滑移率，s为种间距，z为排种盘吸孔数目，i为减速比，N为驱动电机的转速。

直流电机具有调速性能好，控制方式简单、功耗低和性能优良等特点，故本次控制系统中选择直流电机作为播种盘的驱动电机。根据计算得到的电机转速和扭矩，选择了一能机电公司的57BLF-0615NBB无刷直流电机，该电机的主要参数如表1所示。

表1 57BLF-0615NBB无刷直流电机参数Table 1 Parameters of 57BLF-0615NBB brushless DC motor

播种盘控制电机的线电压方程为[7-8]：

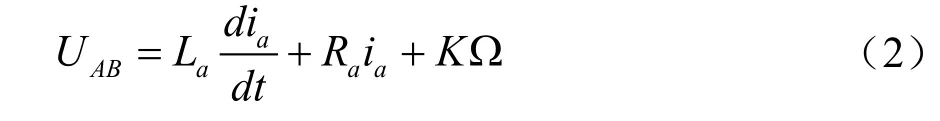
其中，La为相绕组电感，Ra为相绕组电阻，K为反电势系数，UAB为直流母线电压，ia为相电流，Ω为角速度。

电机的运动方程为[7-8]:

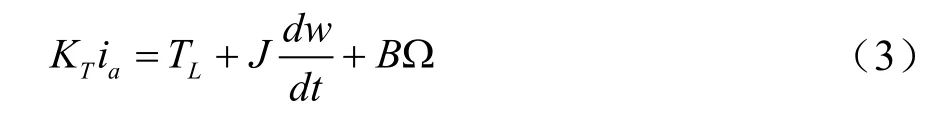
其中TL为负载转矩，KT为转矩常数，J为转子转动惯量，B为黏滞摩擦系数。

当负载为空载的时候，由上面的式子得到播种盘转速控制电机的传递函数为：

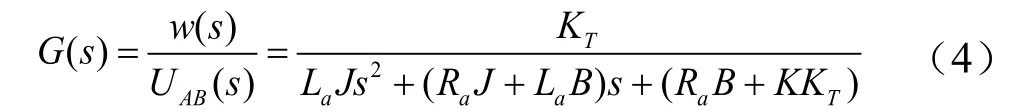
现取Ra=0.2 Ω，La=10 mH，J=1×10-3kg·m2，B=0，KT=0.001，K=0.01，可得到电机的传递函数为：

2 卡尔曼滤波融合遗传PID控制算法

2.1 控制系统结构图

PID控制器输入与输出之间的关系[17]为：

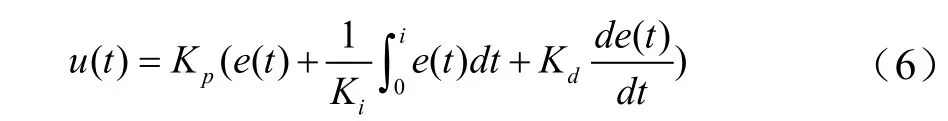
式中，u(t)是控制系统的输出；e(t)表示系统的输入，即给定值与实际输出值之间的差值；Kp表示比例参数；Ki表示积分参数；Kd表示积分参数。

卡尔曼滤波是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法[7-8]。主要由预测方程和更新方程构成[6-9]：

预测方程：

更新方程：

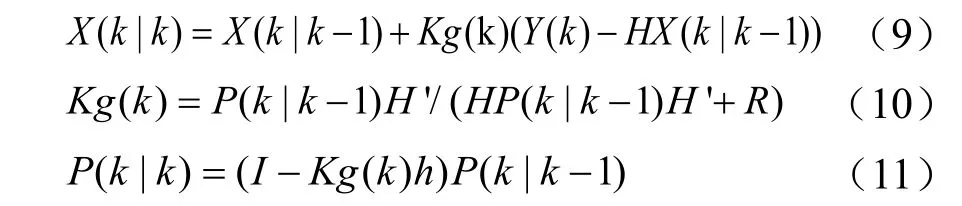
将卡尔曼滤波和传统PID控制相结合可以得到一种基于卡尔曼滤波的PID控制新方法，其系统结构图如图2所示，该控制方法在被控对象与输出之间加了一个卡尔曼滤波器，可以消减控制干扰W和测量干扰V对输出的干扰，从而可以提高系统的性能。

图2 基于卡尔曼滤波的PID控制系统结构图Figure 2 Structure diagram of PID control system based on Kalman filter

2.2 基于遗传算法的PID参数整定

遗传算法是根据大自然生物体进化规律设计提出的，是一种通过模拟自然进化过程搜索最优解的方法，在求解较为复杂的组合优化问题时能够较快地获得较好地优化结果。PID参数是一个典型的多参量组合优化问题，故采用遗传算法对PID控制参数进行整定，以比例、积分和微分的定义域为对象，采用系统误差的绝对值时间积分性能指标作为参数的最小目标函数值，可以较快地获得PID参数的最优解或者最优解的分布区间[13,18-20]，遗传算法的PID参数整定的流程图如图3所示。

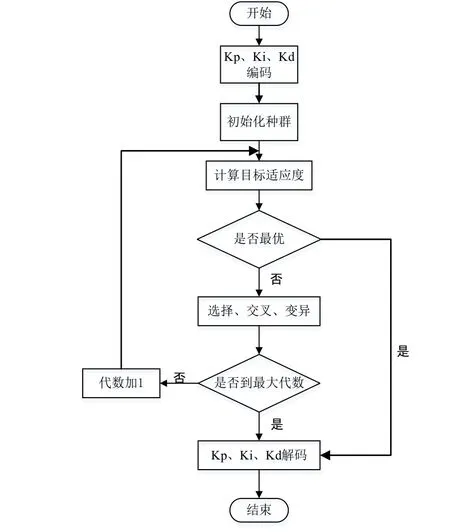
图3 基于遗传算法的PID参数整定流程图Figure 3 PID parameter tuning flow chart based on genetic algorithm

遗传算法寻找最优解的过程大致可以分为编码、种群初始化、计算适应度值、选择复制、交叉变异和解码等几个步骤。按照遗传算法寻找最优解的过程，PID参数整定的方案设计可以分为如下几个步骤[12-13,17-19]：

（1）Kp、Ki、Kd的编码。应用遗传算法寻优时首先面临的问题是参数的编码问题，本次对PID控制参数采用二进制进行编码，用长度为10的二进制序列表示一个参数编码，可以用于表示0～210–1范围内的1 024个数，将Kp、Ki、Kd的编码连接在一起组成30位的二进制编码串，并采用Ziegler-Nichols法初步确定PID参数的寻优区间。

（2）确定适应度函数。参数的最小目标函数值采用的是系统误差的绝对值时间积分性能指标，并将控制输入的平方项加入到目标函数中，目的是为了防止控制能量过大，参数选择的最优指标为：

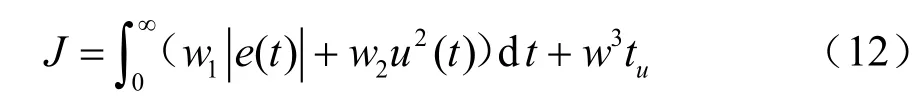
其中，e(t)为系统误差，u(t)为系统输入，tu为上升时间，w1，w2，w3为权值。

在最优指标中加入惩罚因子，避免超调的出现，即在发生超调的时候把超调量作为最优指标的一项，此时最优指标为：

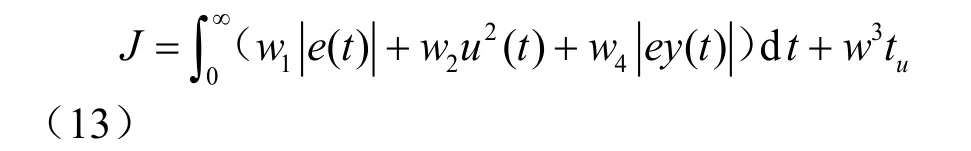
其中，w1，w2，w3为权值，w4为超调惩罚系数，ey(t)=y(t)–y(t–1)，y(t)为系统输出。

由于在遗传算法中需要计算目标适应度值，故需要将最优指标转化为适应度函数，则适应度函数为：

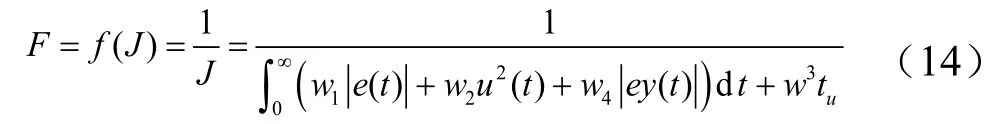
（3）选择。采用适应度值比例法对种群中的个体进行选择，用Ps表示种群中第j个个体被选择复制的概率，其中Ps可以表示为：

其中Fj为第j个个体的适应度值，∑Fj为所有个体的适应度值之和。

（4）交叉与变异。杂交概率Pc和变异概率Pm决定着种群的收敛速度和多样性。为提高种群的多样性，Pc应该取较大值，Pm应该取较小值；为提高种群的收敛速度，Pc应该取较小值，Pm应该取较大值。

（5）再次计算适应度函数值。判断进化的代数是否达到最大迭代数或参数是否已经达到制定的精度，若达到了要求，则结束寻优过程，并对得到的PID控制参数Kp、Ki、Kd进行解码操作，得到全局最优参数Kp、Ki、Kd的值，解码过程如下：

将编码过程中形成的30位编码串分成3部分，用y1表示1～10位二进制编码按20～29权值转化的值，y2表示11～20位二进制编码按20～29权值转化的值，y3表示21～30位二进制编码按20～29权值转化的值，转化为十进制的公式为：

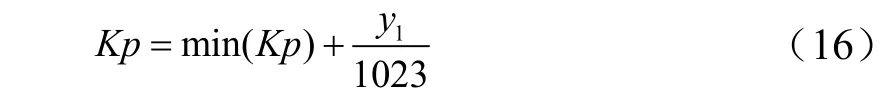
用同样的解码方式即可得到Ki、Kd的最优解。

3 播种盘控制系统仿真

3.1 系统控制流程图

控制系统先采通过遗传算法对PID控制器的参数进行整定，求解出最优的PID控制参数，然后结合卡尔曼滤波算法对系统中存在的干扰和噪声进行滤除，从而实现更加优越的控制，控制系统的流程如图4所示：

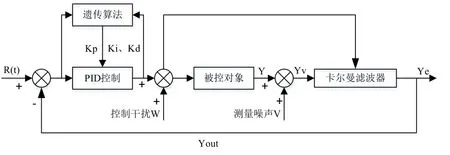
图4 系统控制流程图Figure 4 System control flow chart

3.2 仿真结果与分析

根据建立的播种盘控制电机的数学模型，对排种驱动电机在噪声为0.002和0.1的高斯白噪声下分别进行了4种控制方式的仿真，4种控制方式的仿真依次为传统PID仿真、基于遗传算法的PID仿真、基于卡尔曼滤波的PID仿真和基于卡尔曼滤波遗传算法的PID仿真，并对4种仿真的结果进行了分析比较。

在控制干扰信号W（k）和测量噪声信号V（k）均为0.002的高斯白噪声信号时，假设输入信号为一单位阶跃信号[21]，在卡尔曼滤波器进行信号的滤波处理时，取协方差Q=1，R=1，仿真的时间间隔T取1 ms。通过试凑的方式对PID参数进行整定，可得到PID控制器的参数为：Kp=8.0、Ki=0.8和Kd=0.2；通过遗传算法对PID参数进行整定，可以得到PID控制器参数的最优解为：Kp=19.995 4、Ki=0.021 1和Kd=0.492 8。其阶跃响应曲线如图5所示。

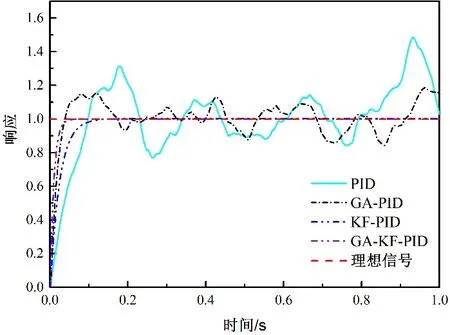
图5 噪声为0.002时仿真结果Figure 5 Simulation results with noise of 0.002

由图5中PID和遗传PID（GA-PID）的仿真曲线可知，通过试凑法得到的仿真结果其响应的波动值最大可达到1.5，而通过遗传算法整定的PID仿真结果其响应的波动最大仅为1.2，通过对比PID和GA-PID的仿真曲线，可知控制系统的响应时间缩短、响应的波动范围减小，因此加入遗传算法的PID控制器的控制效果更加优良。

由图5中PID和融合卡尔曼滤波的PID（KF-PID）的仿真曲线可知，未加入卡尔曼滤波的仿真时，其输出结果会有较大的波动，而加入卡尔曼滤波后，系统的响应波动消失并且很快便趋于平稳。通过对比PID和KF-PID的仿真曲线，可知卡尔曼滤波有效滤除了控制干扰和测量噪声对控制系统的影响，使系统的稳态精度大幅度提高，控制效果得到了明显的改善。

由图5中KF-PID和融合卡尔曼滤波的遗传PID（GA-KF-PID）的仿真曲线可知，未加入遗传算法时，系统的响应时间约为0.15 s，而加入遗传算法后系统的响应时间缩短到0.08 s，通过对比KF-PID和GA-KF-PID的仿真结果，可知通过遗传算法整定的系统相比于试凑法整定的系统调节时间缩短，控制效果得到了明显的改善。

现通过增大噪声，来验证该套算法对于不同的噪声干扰是否同样具有有效性。将控制干扰信号W(k)和测量噪声信号V(k)均改为0.1的高斯白噪声，其余的控制量均保持原来的参数不变。其仿真的结果如图6和图7所示。

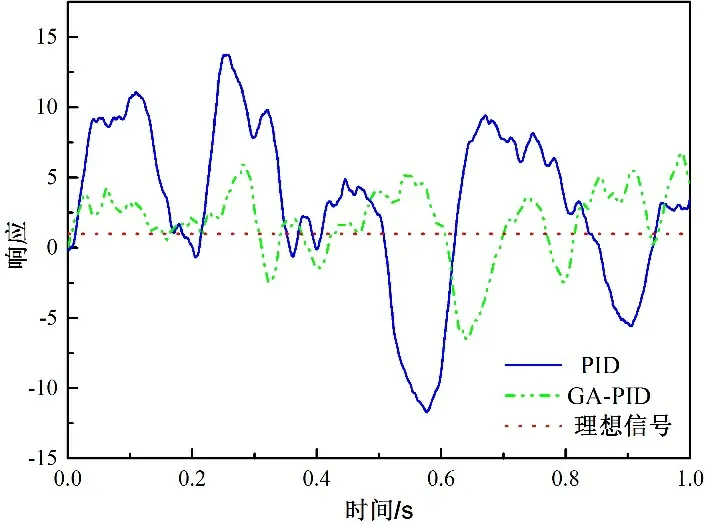
图6 PID与GA-PID仿真结果Figure 6 Simulation results of PID and GA-PID

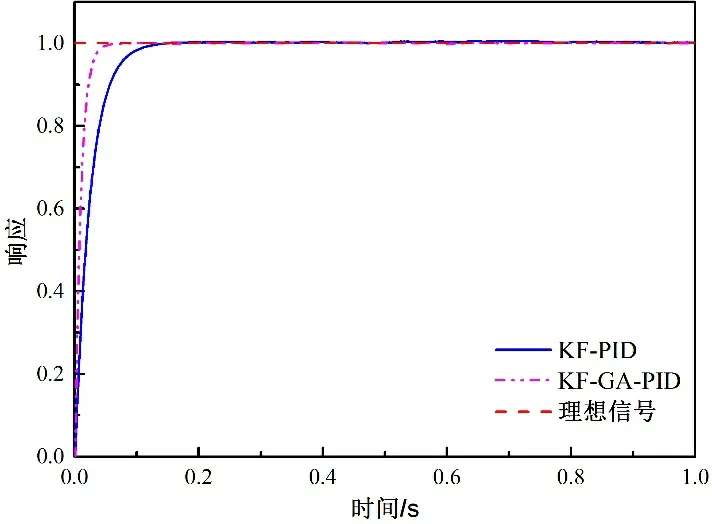
图7 KF-PID与KF-GA-PID仿真结果Figure 7 Simulation results of KF- PID and KF-GA-PID

采用图5相同的分析方法对图6和图7的仿真结果进行对比分析，可以得到在噪声为0.1时，该套算法在改善控制系统的控制效果上依然有效。结合图5、图6和图7的仿真结果，可以得出该套算法在不同的控制干扰信号W(k)和测量噪声信号V(k)下都是有效的，即可说明此算法在各种工作状况下用于提高播种机播种效果都是有效果的。