负载条件下纤维加筋土单根纤维拉拔特征及性能

2021-10-14杨晓松韩志强

科学技术与工程 2021年27期

黎亮，杨晓松，王成，韩志强

(塔里木大学水利与建筑工程学院，阿拉尔 843300)

道路基础建设的高质量绿色发展必然对路基提出更高的要求。在填土中掺合一定比例的纤维以改善土的物理力学性质的纤维加筋土具有就地取材，减少填料运输和使用等优点，在未来的路基建设中具有重要潜力。因此，许多学者就纤维加筋土的物理力学性能及改良做了大量研究。

苏帅等[1]、韩春鹏等[2]、何钰龙等[3]的研究结果表明纤维加筋土不仅可以抑制土体的竖向和侧向变形，还可以有效提高土体的抗压和抗拉特性、抑制膨胀土脆性开裂、改善冻土区路基的性能。阮波等[4]、张军等[5]等的研究表明纤维的加入提高了土体黏聚力进而提高了纤维加筋土体抗剪强度。尹锦明等[6]研究发现通过提高纤维加筋土路基的击实功，可以提高纤维加筋作用，改善纤维加筋土路用性能。曾军等[7]研究表明纤维长度越长,掺入量越多加筋效果越好。陈佳雨等[8]通过正交试验确定了纤维加筋土强度的影响因素的优先级，依次为含水率、干密度、纤维掺量、纤维长度。

除了纤维加筋土宏观的物理力学性能研究之外，部分学者对纤维加筋机理进行了阐释与研究。张艳美等[9]将纤维的补强机理概括为弯曲机理和交织机理。王德银等[10]、唐皓等[11]则将纤维的补强机理凝练为单根纤维一维拉筋作用和纤维网三维拉筋作用。然而，唐朝生等[12]认为纤维的加筋补强基础在于界面间的摩擦力和黏结力大小，弄清楚纤维-土界面作用对阐明纤维加筋机理尤为重要，因此，其开展了单根直线形纤维的拉拔试验并确定纤维加筋土界面作用；张诚成等[13]根据纤维拉拔试验建立了纤维渐进破坏数学模型。

在实际纤维加筋土工程中，例如高填方路基和挡土墙等，纤维加筋土都处于负载状态。目前中外岩土工程领域关于纤维-土界面力学作用鲜有考虑负载应力的定量研究。为了理清负载条件下纤维加筋土纤维-土界面作用规律与机制，设计负载纤维加筋土单根纤维拉拔试验装置和试验方法，定量分析负载应力，纤维长度对纤维拉拔特征及界面抗剪强度的影响。

1 试验材料与方法

1.1 试验材料

为了制样方便且减小土样差异而引起的试验结果波动，本次试验选用的土样为风力分选良好的风积沙，取自塔克拉玛干沙漠边缘。该土样粒径主要分布在0.075～0.125 mm，占总质量的96%以上，土样粒径级配如表1所示。

表1 风积沙粒径级配分布表Table 1 Grain size distribution table of aeolian sand

试验中选用的纤维为尼龙纤维，此种纤维相较于普通的聚丙烯纤维具有极低的延展性，因此可以减少纤维拉拔过程中由于纤维自身变形对拉拔力-位移曲线的影响，纤维性能参数如表2所示。

表2 纤维性能参数Table 2 Fiber performance parameter

1.2 试验装置和试验方法

自行设计的单根纤维负载拉拔装置如图1所示，主要由升降仪、电子天平，以及纤维加筋土加载器件组组成。升降仪由多功能工程力学组合试验平台改装完成，位移控制精度为0.05 mm；电子天平测量精度为0.01 g；纤维加筋土加载器件组主要包括土壤加载装置(土壤直剪仪改装完成)和土样室，可以对纤维加筋土提供100、200、300、400 kPa的上覆压应力σ，由于土样室尺寸为Ф61.8 mm×40 mm且侧向刚度极大，可以保证土样的竖向应力均匀。

①为升降仪；②为滚轴；③为升降平台；④为电子天平；⑤为配重块； ⑥为拉伸导线；⑦为加载盖；⑧为纤维；⑨为土样宝；⑩为土样室底座图1 试验仪器原理图Fig.1 Schematic diagram of test instrument

试验仪器工作原理为：①通过土壤加载装置对加载盘施加指定荷载使土样室内的纤维加筋土均匀受力达到指定负载应力；②通过升降仪控制升降平台下降，在自重作用下升降平台上的电子天平和配重块跟随升降平台下降相同的高度，在此过程中，拉伸导线通过滚轴对土中纤维进行水平拉拔，拉拔力等于电子天平上配重块重力的减少值(纤维拉拔力等于拉伸导线对配重块的上提作用力)，纤维拉拔位移等于升降仪下降位移。

实际操作过程中，通过电子天平采集到的数据反映的是配重块质量的变化，因此，需要转换为纤维所受的拉力，即

N=0.98×10-3(R0-R)

(1)

式(1)中：R0和R分别为天平的初始读数和试验开始后天平的读数，g；N为纤维所受的拉力，N。

纤维与土之间的界面剪切强度为

(2)

式(2)中：τ为纤维-土界面抗剪强度；Fmax为线性阶段峰值拉拔力；S为纤维与土接触面积；D为纤维直径；L为纤维长度。

1.3 制样

按照《土工试验方法标准》(GB/T 50123—2019)规定进行风积沙击实试验，得到不同含水率条件下的风积沙干密度。考虑试验的稳定性，本文中选取含水率为10%，对应干密度为1.5 g/cm3的风积沙湿土样作为试验土样。土样室高40 mm且在其中部开有2 mm小孔[图2(a)]，以便纤维穿入。制样时，根据土样室体积算出湿土样总质量；取总质量的一半倒入土样室并击实至土样室高度的一半[图2(b)]；将一根尼龙纤维从土样室中部小孔穿入指定长度[图2(c)]；将剩余土样倒入土样室并击实至土样室顶平齐[图2(d)]，试样示意图如图3所示。

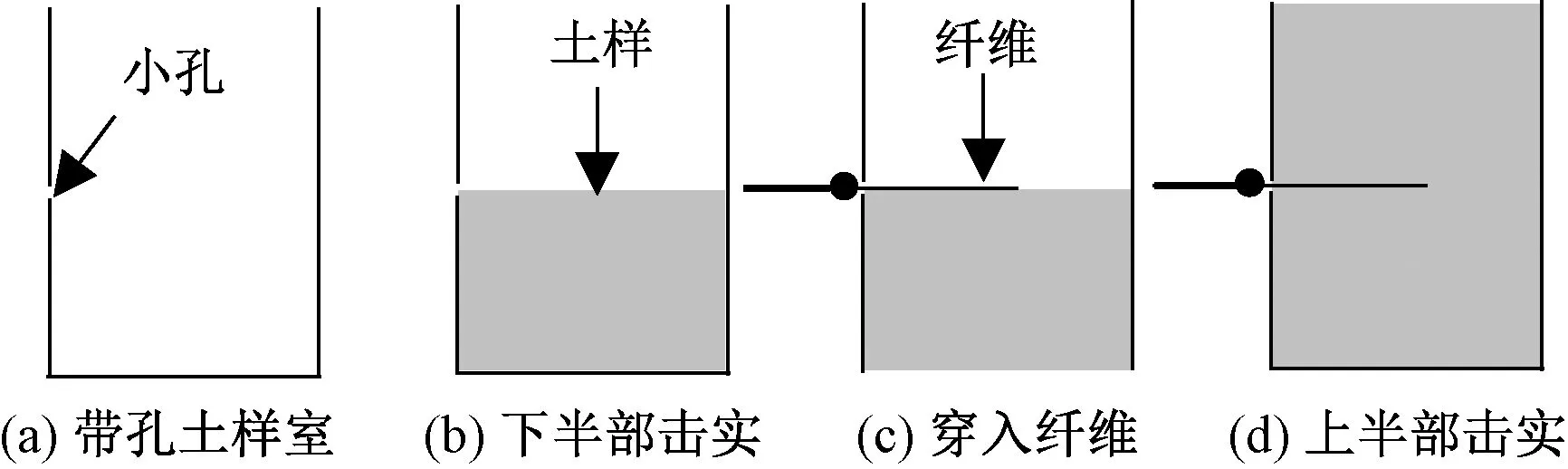
图2 土样制备过程示意图Fig.2 Sketch drawing of sample preparing process

图3 单根纤维拉拔试验样品示意图Fig.3 Sketch drawing of single fiber pull-out test sample

1.4 试验方案

试验采用位移控制，位移速率为0.05 mm/s,设置负载应力为100、200、300、400 kPa;纤维长度为1、2、3、4 cm；共计16组试验，每组至少3个平行样。

2 试验结果分析

2.1 拉拔特征

如图4～图6所示，负载条件下，纤维整个拉拔过程大致分为三个阶段：线性阶段、屈服阶段和软化阶段。当拉拔位移较小时，拉拔力与位移服从线性关系，为线性阶段；该阶段最大拉力为线性峰值拉力Fmax，最大位移为线性峰值位移Δmax，拉拔力与位移的比值为线性斜率Kx。当位移超过线性峰值位移，拉拔力随着位移的增加缓慢变化且成非线性关系，为屈服阶段。当拉拔位移增加到一定程度，拉拔力与位移又恢复线性相关性，拉拔力随着位移的增加而降低，为软化阶段，拉拔力与位移的比值为软化斜率Kr。

图4 纤维拉拔曲线示意图Fig.4 Sketch drawing of single fiber pull-out curve

2.1.1 纤维长度对拉拔特征的影响

如图5所示，线性阶段，随着纤维长度L的增加，线性峰值位移Δmax随之增加，但绝对位移Δ较小，主要集中在1.0～3.0 mm之间，这说明负载条件下很小的纤维-土界面相对位移就能产生较大的界面相互作用。在此阶段，不同长度纤维拉拔力-位移曲线基本重合，100、200、300、400 kPa负载条件线性斜率Kx分别为0.425、0.49、0.45、0.50 N/mm，差异不大；这说明拉拔力随位移增加的增长速率受纤维长度影响较小。

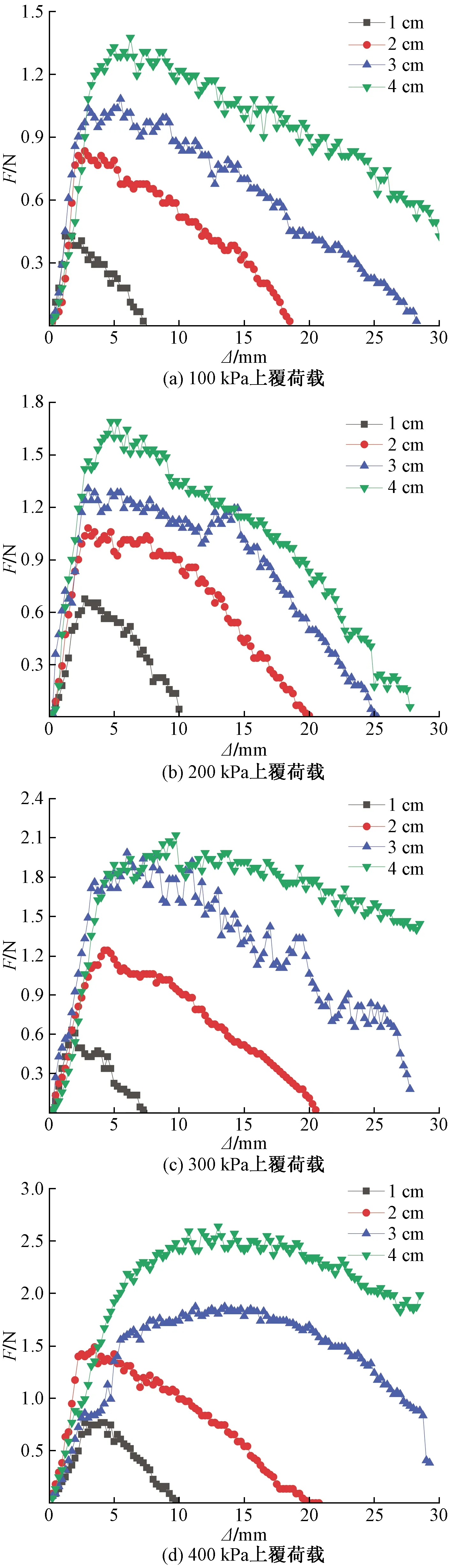
图5 不同长度纤维拉拔曲线图Fig.5 single fiber pull-out curve with different fiber length

屈服阶段，拉拔力-位移曲线呈现非线性特征，纤维长度越大，曲线曲率越小。屈服区间越大。

软化阶段，拉拔力随着拉拔位移的增加呈现出线性下降的趋势，但该阶段的软化斜率绝对值|Kr|显著小于线性阶段的线性斜率Kx。100、200、300、400 kPa负载条件下，|Kx/Kr|分别在5～11、5～7、4～12、4～8之间不等；纤维长度对软化斜率有明显的影响，相同负载应力条件下，随着纤维长度越长，软化阶段曲线有逆时针旋转的趋势，即相同负载条件下，纤维越长，软化斜率Kr的绝对值越小，曲线越平缓。100 kPa负载条件下，当纤维长度由1 cm增加到4 cm，软化斜率绝对值由0.08 N/mm降低到0.04 N/mm；200 kPa负载条件下，软化斜率绝对值由0.1 N/mm降低到0.07 N/mm；300 kPa负载条件下，软化斜率绝对值由0.12 N/mm降低到0.004 N/mm；400 kPa负载条件下，软化斜率绝对值由0.15 N/mm降低到0.07 N/mm(图6)。

图6 Kr-L曲线Fig.6 Curve of Kr-L

2.1.2 负载应力对纤维拉拔特征的影响

如图7所示，线性阶段，不同负载应力σ条件下纤维拉拔力-位移曲线基本重合。1、2、3、4 cm长度纤维线性斜率依次为0.38、0.55、0.52、0.49 N/mm。

图7 不同负载应力条件下纤维拉拔曲线图Fig.7 Single fiber pull-out curve under different loads

100、200 kPa负载应力区间屈服阶段跨度很小，屈服阶段不明显，300、400 kPa负载应力区间屈服阶段跨度较大，曲线曲率很小，甚至有近似水平的波动段。

软化阶段，拉拔力-位移曲线呈现出线性下降的趋势。整体上看，随着负载应力的增加，软化斜率Kr的绝对值增加，但变化特征受到纤维长度的显著影响。当纤维长度为1 cm时，软化斜率绝对值随着负载应力的增加单调线性递增。当纤维长度为2、3、4 cm时，随着负载应力的增加，软化斜率绝对值成两阶段变化：负载应力从100 kPa增加到200 kPa时，其快速增加，负载应力从200 kPa增加到400 kPa时，其缓慢变化，如图8所示。

图8 Kr-σ曲线Fig.8 Curve of Kr-σ

综上所述，纤维拉拔过程分为三个阶段，线性阶段拉拔力随拉拔位移的增加线性增加。线性斜率在不同的纤维长度和负载应力条件下均在0.5 N/mm左右，可以由此推论纤维的线性斜率受负载应力和纤维长度的影响较小。纤维长度和负载应力的增加都会使屈服阶段的曲线曲率减少，区间增大。纤维长度的增加会引起软化斜率绝对值的降低；负载应力的增加会引起软化斜率绝对值的增加。

2.2 纤维长度对拉拔性能的影响

峰值拉拔力Fmax和界面抗剪强度σ是纤维加筋土设计的两个重要参数，如图9、图10所示：相同负载条件下，峰值拉拔力随着纤维长度的增加单调递增，且两者之间表现出良好的线性相关性；负载应力越大，峰值拉拔力-纤维长度曲线斜率越大，即负载越大，峰值拉拔力随着纤维长度的增加增长得越快，当负载应力从100 kPa增加到400 kPa时，峰值拉拔力-纤维长度曲线斜率从0.31 N/cm增加到0.46 N/cm。

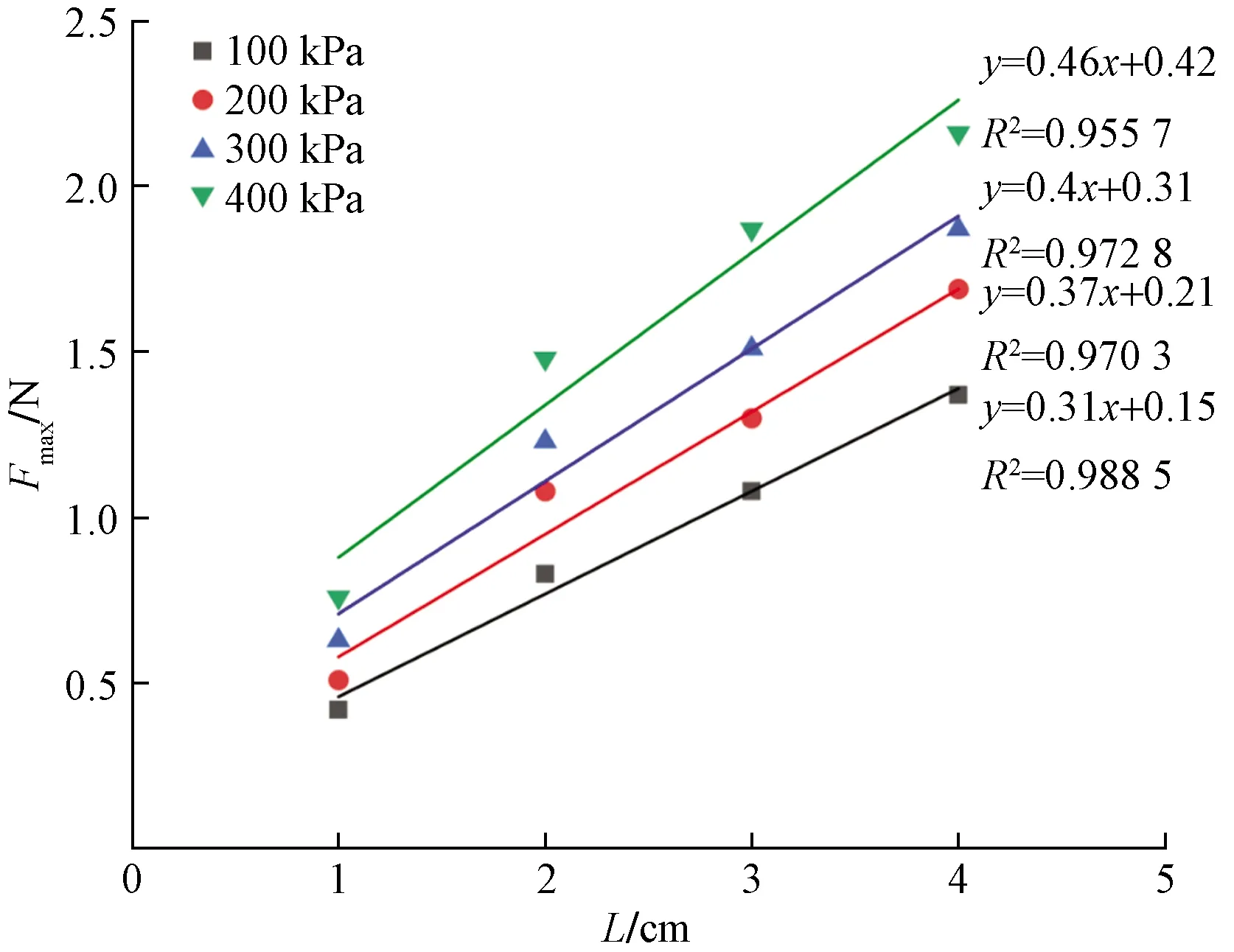
图9 Fmax-L曲线Fig.9 Curve of Fmax-L

图10 τ-L曲线Fig.10 Curve of τ-L

与峰值拉拔力随着纤维长度变化规律不同，纤维-土界面抗剪强度随着纤维长度的增加单调降低，且负载应力越大，降低得越快，当负载应力由100 kPa增加到400 kPa,界面抗剪强度-纤维长度曲线斜率由-8.72 kPa/cm降低到-23.56 kPa/cm。

综上所述，纤维长度的增加能增加纤维-土界面总的作用力，但总作用力的增加速率小于纤维长度的增加速率，最终导致单位面积的抗剪强度随着纤维长度的增加而降低。

2.3 负载应力对拉拔性能的影响

试验结果表明：纤维长度相同的条件下，随着负载应力的增加，峰值拉拔力和界面抗剪强度均呈现出单调增长的趋势；但不同的是，纤维长度越长，峰值拉拔力随着负载应力的增加增长得越快，界面抗剪强度随着负载应力的增加增长得越慢。纤维长度由1 cm增长到4 cm, 峰值拉拔力-负载应力曲线斜率由0.001 1 N/kPa增加到0.002 6 N/kPa；抗剪强度-负载应力曲线斜率由0.35降低到0.19，如图11、图12所示。