基于径向基神经网络的主动前轮转向自抗扰控制
2021-10-14孔博龙帕孜来马合木提王加健
孔博龙, 帕孜来·马合木提, 王加健
(新疆大学电气工程学院, 乌鲁木齐 830047)
随着国民生活水平的提高以及汽车技术的发展,人们对车辆舒适性和安全性的要求也在不断提升。汽车的横向稳定性作为评价汽车安全行驶的性能指标,研究车辆横向稳定性的控制显得尤为重要[1]。主动前轮转向系统(active front wheel stee-ring,AFS)作为未来转向系统发展的主要方向之一,基于横向稳定性控制研究汽车主动前轮转向就愈加重要。AFS是在方向盘输入转角的基础上根据实时理想横摆角速度和实际横摆角速度通过增加独立于驾驶员的附加转角改变车辆的横向受力状态。从目前的研究看,制约AFS性能的因素主要是控制策略的设计[2],霍春宝等[3]提出遗传算法优化的主动转向控制,利用遗传算法优化反向神经网络,克服反向神经网络收敛速度慢和易陷入局部最优;夏长高等[1]针对传统滑模控制产生的“抖振”利用径向基神经网络(radial basis function neural network,RBFNN)对其切换增益进行实时调节抑制“抖振”现象提高控制器控制效果;桑楠等[4-6]针对车辆行驶过程的扰动提出自抗扰控制技术的主动前轮转向系统。
考虑车辆实际行驶环境复杂、干扰状况未知等因素。基于前人的研究,采用RBF神经网络在线整定自抗扰控制(auto disturbance rejection control, ADRC)的部分参数保证ADRC品质,提高控制器对参考横摆角速度的跟踪能力;同时设计AFS变传动比规则改善驾驶轻便、灵敏性,提高驾驶安全性。
1 主动前轮转向系统
1.1 车辆二自由度参考模型
为体现车辆理想的侧向运动,建立线性二自由度车辆模型作为参考模型[7],线性二自由度模型式为
(1)
式(1)中:m为汽车质量, kg;Iz为绕z轴的转动惯量, kg/m2;k1、k2分别为前后轮侧偏刚度, N/m;a、b分别为前后轴到汽车质心的距离,m;ωr为横摆角速度,rad/s;β为车身质心侧偏角,rad;δf为前轮转角, rad;u为车辆沿x轴方向的速度即车辆前进速度,m/s。
对式(1)两边求导,质心侧偏角足够小时,
(v为二自由度车辆侧向速度)代入整理得
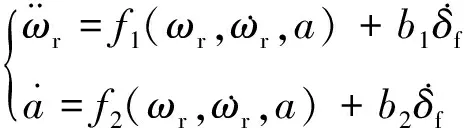
(2)
1.2 主动转向的实现
汽车主动转向系统主要由转向盘、主动转向电机、双排行星齿轮系、助力电机ECU(electronic control unit)、蜗轮蜗杆机构、转向角传感器等部件组成[8-9]。汽车主动转向系统原理图,如图1所示。
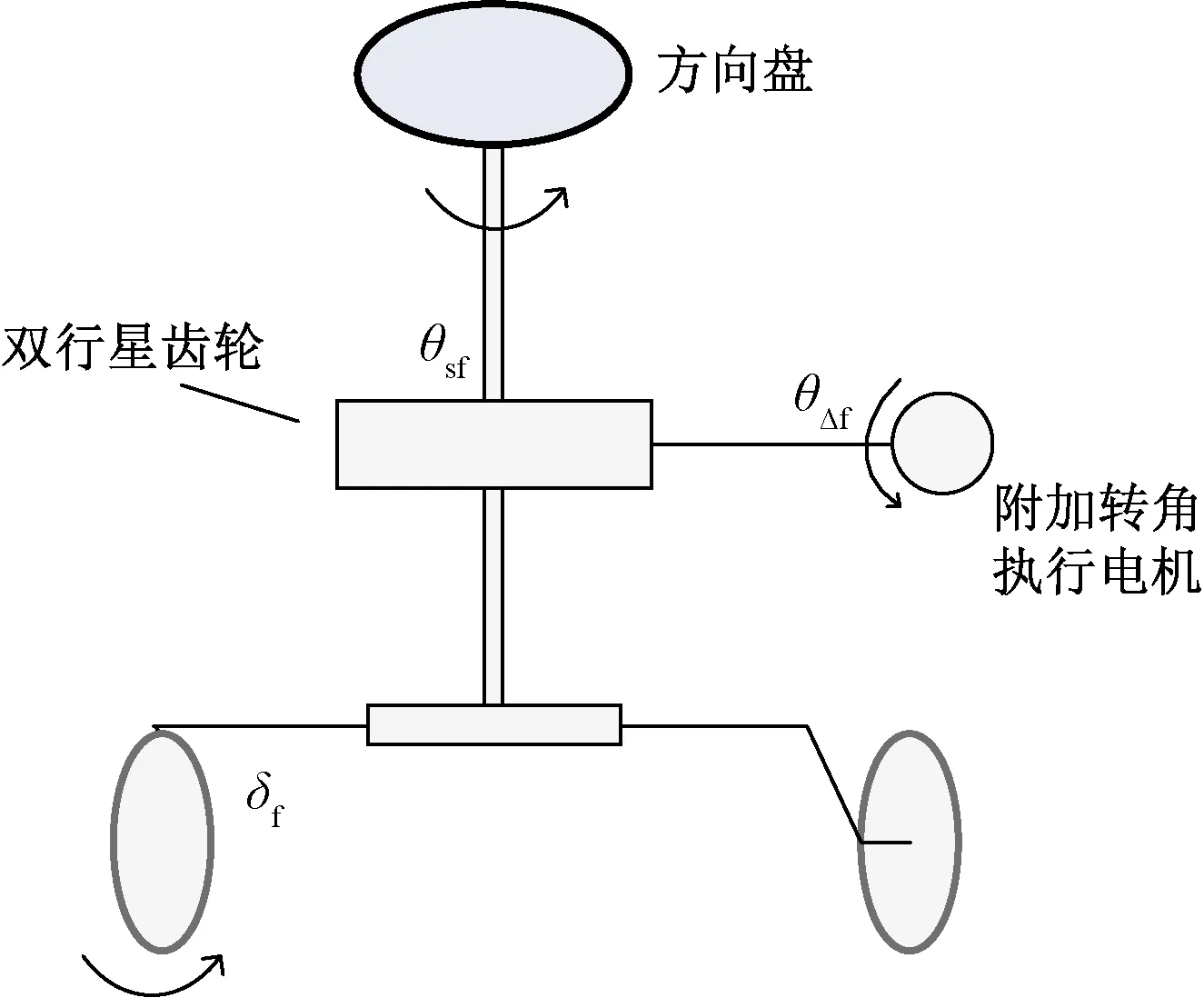
图1 汽车主动转向系统原理图Fig.1 Schematic diagram of automobile active steering system
汽车主动转向的控制是根据车辆行驶状态,把转向盘转角和车速信号输入给AFS执行电机,通过施加附加前轮转角,其中δf、θsf、θΔf分别为车辆前轮转角、驾驶员方向盘输入和附加前轮转角,G为转向器传动比。改善车辆的侧向动态特性。该系统是在传统转向系统的方向盘与机械转向器之间嵌入一个二自由度的双排行星齿轮机构,从而实现车辆的主动转向。主动前轮转向系统车辆前轮转角δf=δsf+δΔf,δsf为转向盘转角产生的前轮转角,驾驶员方向盘输入θsf=Gδsf。
2 理想变传动比规则设计
设计理想变传动比规则,避免低速时的转向迟滞和高速时的转向过灵敏现象,而降低由此造成的事故发生率。
当车辆处于稳定状态时其横摆角速度ωr为定值,则
代入线性二自由度微分方程得理想横摆角速度,即

(3)
式(3)中:l为轴距,l=a+b;K是稳定性因数,K=m/l2(a/k2-a/k1)。
所以,稳态横摆角速度增益可表示为

(4)
在车辆理想变传动比转向控制中,基于固定横摆角速度增益设计的变传动比称为车辆的理想变传动比。原联邦德国的几个研究所通过对轿车进行实验后统计得出:轿车的稳态横摆角速度增益Gsw=0.16~0.33 s-1,相应的试验工况为:u=22.35 m/s,a=0.4g(g为重力加速度)。当Gsw=0.32 s-1时汽车的操纵稳定性变化较小,更有利于减轻驾驶员负担[10],本文取Gsw=0.32 s-1设计变传动比策略。
固定横摆角速度增益的传动比为
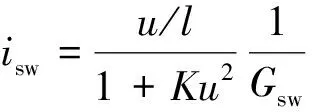
(5)
车辆在市区行驶一般速度为30 km/h,在高速上车速不能超过120 km/h,则以30 km/h和 120 km/h 为临界速度设置传动比,其对应的传动比范围为9.1~26.4,则理想变传动比曲线如图2所示。

图2 理想变传动比曲线Fig.2 Ideal variable transmission ratio curve
其规则方程式为
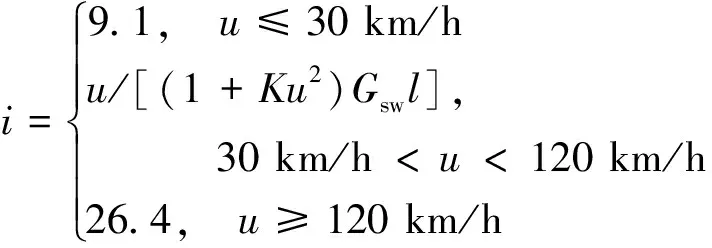
(6)
3 RBF神经网络的自抗扰控制器设计
本文车辆的主动转向控制,是实际车辆横摆角速度与理想的横摆角速度通过RBF神经网络自抗扰控制器计算得到附加前轮转角,实现对理想的横摆角速度进行跟踪。控制结构如图3所示。
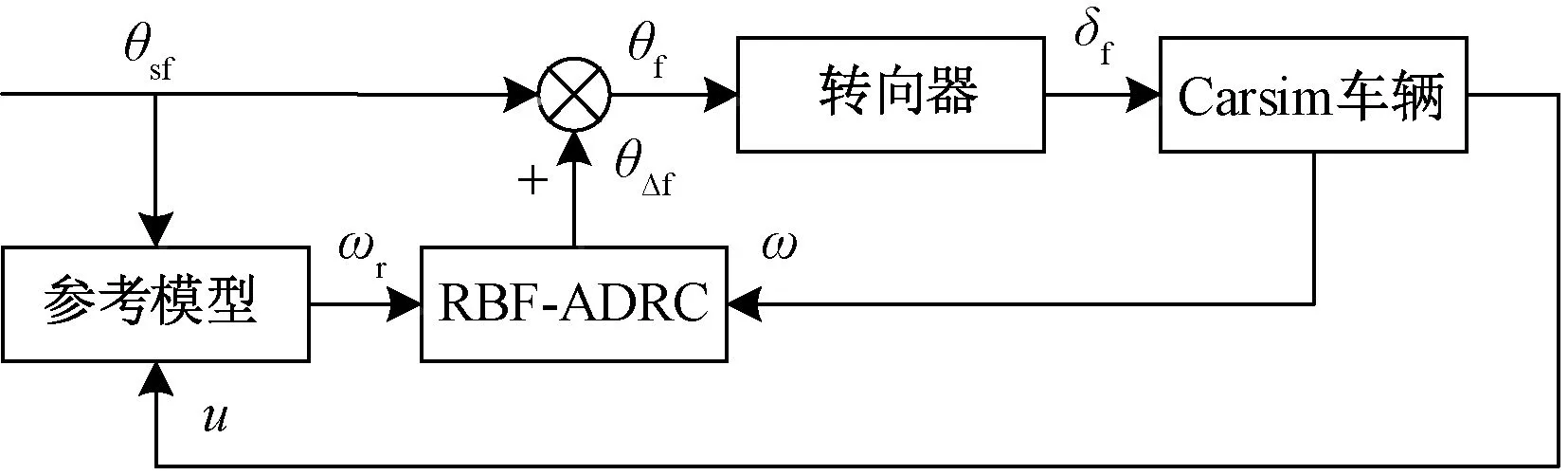
图3 主动前轮转向控制结构Fig.3 Control structure of active front wheel steering
3.1 自抗扰控制器设计
自抗扰控制把系统中车辆实际运行未建模的动态部分和未知的外界扰动作用都归结为对系统的“总扰动”利用扩展状态观测器(extended state observer,ESO)对其实时估计并对系统给予补偿,从而提升控制效果和精度[11]。
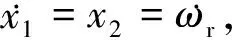

(7)
通过微分环节得到输入信号γ1和其微分信号γ2,微分环节可表示为
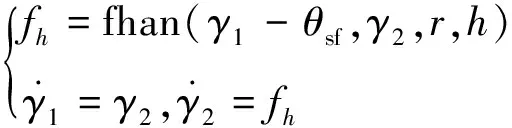
(8)
微分跟踪器函数为最速综合函数fhan(x1,x2,r,h),见文献[12]。
在车辆主动转向系统中设计二阶自抗扰控制器跟踪理想横摆角速度,控制器设计步骤如下。
TD:能够在外界干扰的影响下根据设定的输入信号ωr获得比较平稳的输入信号v1及其微分信号v2用于自抗扰控制的状态误差反馈。
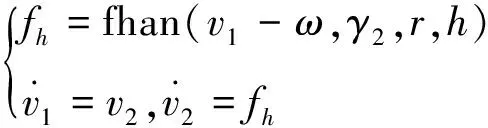
(9)
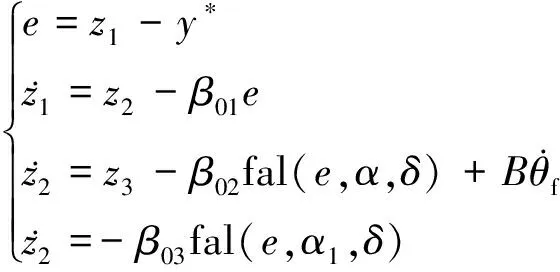
(10)
非线性函数fal表达式为

(11)
式中:α、δ均为正数。

NLSEF:非线性组合将TD信号v1、v2与ESO状态变量信号z1、z2进行非线性组合,从而得到非线性状态误差反馈控制量u0,u0与总扰动补偿量结合形成总控制量u。
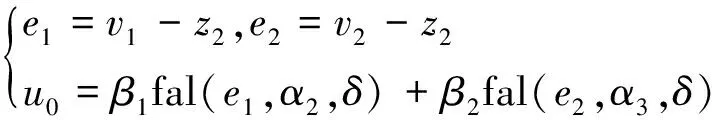
(12)
对误差反馈控制量u0,用总扰动估计值z3的补偿来决定最终控制量U
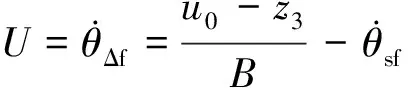
(13)
3.2 RBF神经网络自抗扰控制器参数自整定设计
选用n-m-1型的3层RBF神经网络结构调节ADRC核心部分ESO中的参数β01、β02、β03,n、m、1分别为输入层、隐含层、输出层节点个数。设计一个由RBF自整定ADRC参数的主动转向控制器。基于RBF-ADRC的主动转向系统结构如图4所示。

图4 主动前轮转向系统RBF-ADRC控制结构Fig.4 RBF-ADRC control structure of active front wheel steering system
径向基函数选取标准高斯函数,表达式为
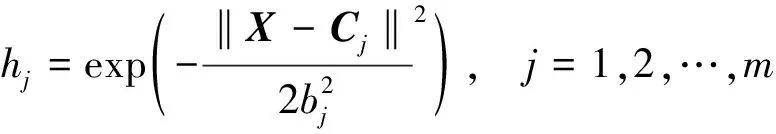
(14)
式(14)中:X=[x1,x2,…,xn]为网络的输入向量;Cj=[cj1,cj2,…,cjm]为网络中第j个节点的中心矢量;bj为第j个节点的基宽。
RBF神经网络输出为
ym(k)=ω1h1+ω2h2+…+ωmhm
(15)
式(15)中:ω=[ω1,ω2,…,ωm]T为网络输出层的权值向量。
选取网络性能指标为
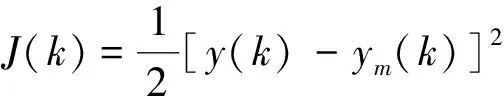
(16)
式(16)中:y(k)为系统输出;ym(k)为RBF神经网络输出。
采用梯度下降法修正网络参数,算法为
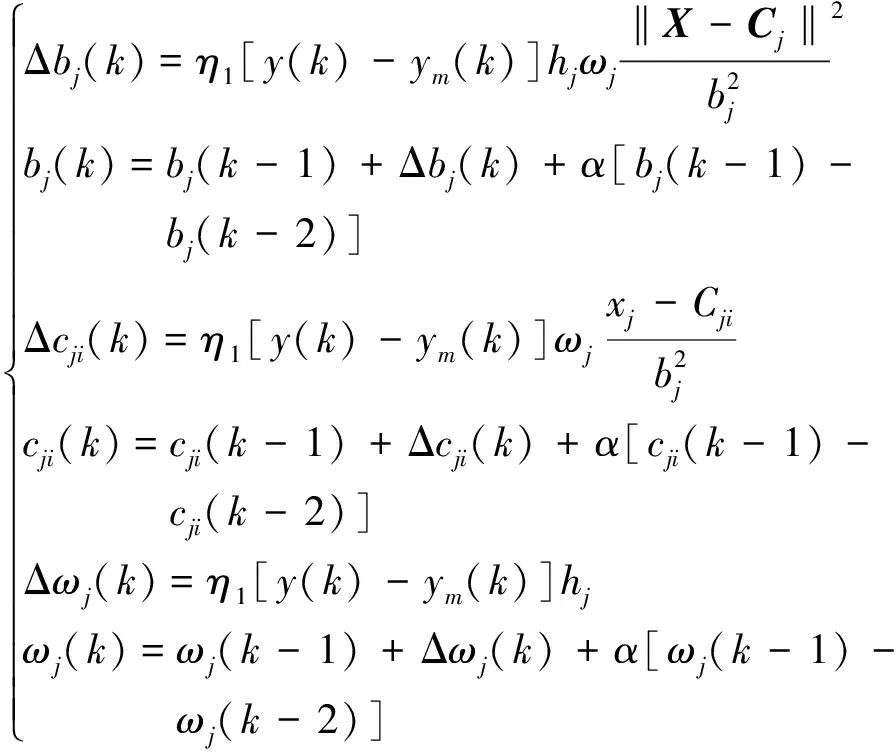
(17)
式(17)中:η为学习效率;α为动量因子。
为调整ESO的权值系数,选取性能指标函数为
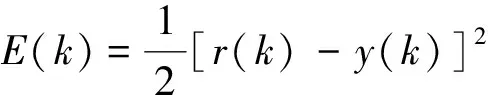
(18)
式(18)中:r(k)为系统的输入信号;y(k)为系统的输出信号。
RBF神经网络Jacobian矩阵算法为
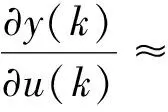
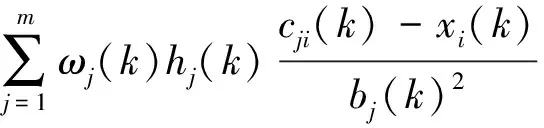
(19)
RBF神经网络结构对自抗扰控制器ESO参数β01、β02、β03整定及主动前轮转向控制步骤如下。
步骤一确定ADRC和RBFNN结构并初始化相应参数。
步骤二获取理想横摆角速度ωr并采集Carsim车辆的控制量U和实际横摆角速度ω。
步骤三计算RBFNN的输出值与实际横摆角速度的偏差,偏差满足性能指标转步骤五,否则转步骤四。
步骤四修正RBFNN网络中心矢量、基宽向量、权值向量。
步骤五计算Jacobian信息。
步骤六梯度下降法调整ESO参数β01、β02、β03值,输出控制器最优参数。
步骤七控制器计算并输出所需附加转角。
步骤八Carsim车辆实际横摆角速度ω与参考横摆角速度ωr,是否存在误差,是,转步骤二;否则结束。
4 实验仿真验证与分析
利用MATLAB/simulink和Carsim联合仿真平台搭建主动前轮转向控制系统,在MATLAB/simulink中搭建RBF自抗扰控制器和二自由度车辆模型运用Carsim环境中整车模型完成实验仿真验证,整车模型主要参数,如表1所,仿真模型如图5所示。

图5 CarSim/Simulink 联合仿真模型Fig.5 CarSim / Simulink co-simulation model

表1 整车模型主要参数
4.1 理想变传动比实验
根据现实不同环境下对车速的要求设计理想变传动比规则,与传统固定传动比在主动转向控制中的仿真分析对比。设置正弦转向盘输入模拟车辆蛇形工况,正弦输入幅值30°,周期为5 s,分别在不同速度段取20、80、130 km/h作为车辆仿真速度,仿真结果如图6所示。

图6 不同车速下的正弦输入响应Fig.6 Sinusoidal input response at different vehicle speeds
由仿真结果可以看出,车速为20 km/h时,与固定传动比相比理想变传动比的横摆角速度、质心侧偏角、侧向加速度的响应幅值更大,说明理想变传动比在低速时提升了转向灵敏度使得驾驶员驾驶状态更轻松。车速为80 km/h和130 km/h时,理想变传动比的横摆角速度、质心侧偏角、侧向加速度的响应幅值均比固定传动比小,表明理想变传动比在高速时车辆转向稳定性更好,能给驾驶员提供更强的路感。
4.2 抗测风干扰实验
实验车速设置u=60 km/h,路面附着系数μ=0.8直线行驶,随机侧向风模型如图7所示。

图7 随机侧向风模型Fig.7 Random lateral wind model
如图8所示为车辆正常行驶中受侧向风干扰在不同控制器作用下的横摆角速度跟踪曲线,可以看出RBF-ADRC控制能有效抑制侧风对车辆横向稳定的影响。由表2抗干扰工况仿真实验数据可以直观看出RBF-ADRC控制的横摆角速度抗干扰量百分比为95%,比ADRC控制的69.2%提高了25.8%。
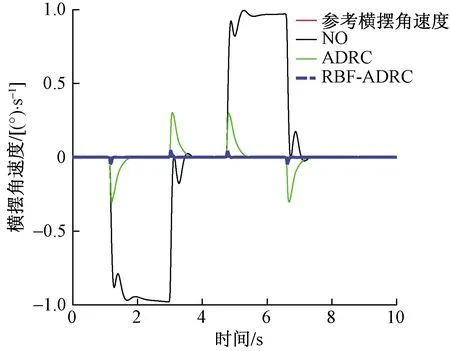
图8 抗外扰实验Fig.8 Anti disturbance experiment
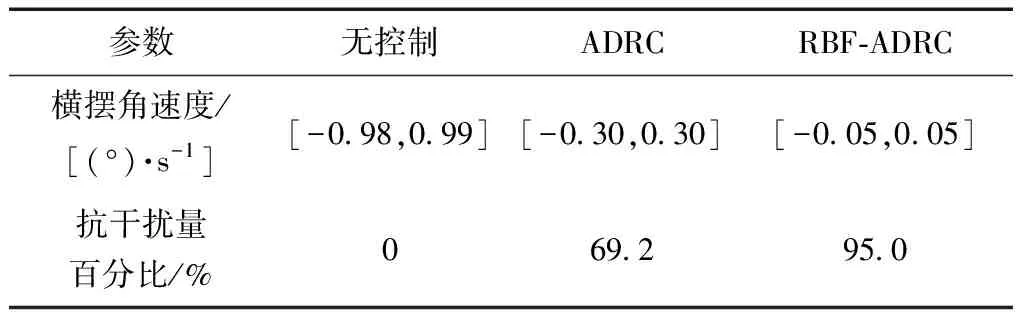
表2 抗干扰工况仿真实验数据
4.3 双移线工况
在双移线工况实验中设置车速u=80 km/h,路面附着系数为0.8验证RBF神经网络自抗扰控制车辆主动转向的有效性。仿真实验的方向盘转角输入如图9所示。仿真结果如图10所示,其中由图10(a)可以看出RBF-ADRC控制下对理想横摆角速度的跟踪效果优于ADRC和无控制。由此可见,RBF-ADRC能更好地降低车辆横摆角速度峰值提高车辆横向稳定性;由图10(b)、图10(c)可知,基于RBF-ADRC控制的侧向加速度和质心侧偏角相比ADRC和无控制,波动幅度最小、收敛速度更快。实验表明,基于RBF神经网络的自抗扰控制器提高了车辆在双移线工况下行驶的稳定性。
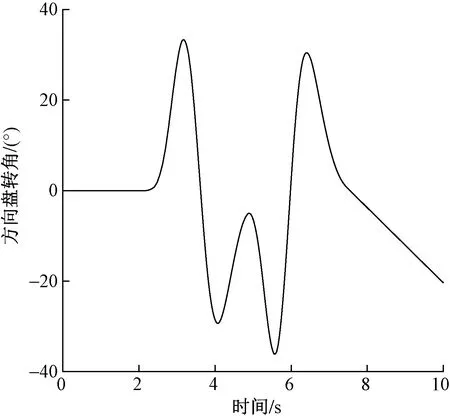
图9 双移线工况方向盘转角输入Fig.9 Steering wheel angle input under double lane shifting condition

图10 双移线工况下实验仿真曲线Fig.10 Experimental simulation curve under double line shifting condition
5 结论
在汽车AFS稳定性控制研究中,设计基于RBF神经网络的自抗扰控制策略,通过实验仿真结果得到以下结论。
(1)理想变传动比规则相对于固定传动比,在低速时提高了驾驶员操作灵敏度高速时增强驾驶员驾驶路感。
(2)利用RBF神经网络能在线调整ADRC中ESO的参数,提高ESO的状态观测能力保证了ADRC的品质。
(3)基于RBF神经网络的自抗扰控制策略能实现对理想横摆角速度的良好跟踪,相对于普通ADRC横摆角速度抗干扰量提升了25.8%,降低了横摆角速度的振荡幅值,改善了车辆的可控性和稳定性。
