基于开源求解工具的超临界二氧化碳印刷电路板式换热器流动传热特性数值研究

范世望， 朱郁波， 周 璐， 刘 杰， 钱娱佳， 闵皆昇

(1.上海汽轮机厂有限公司， 上海 200240； 2.浙江远算科技有限公司， 杭州 310012)

近年来，众多科研与工程人员针对使用超临界二氧化碳(sCO2)作为工质的布雷顿循环发电技术开展了广泛的研究。相比于普遍应用的蒸汽朗肯循环发电技术，sCO2布雷顿循环发电技术实现了发电效率显著提高，设备结构紧凑、尺寸显著缩小等优点。在sCO2布雷顿循环中，压缩机、透平等设备尺寸都较小，而传统换热器尺寸较大，为了满足整个系统的尺寸要求，一般选择结构更加紧凑、耐高温高压的印刷电路板式微通道换热器(printed circuit heat exchanger，PCHE)。在相同的热负荷下，PCHE与传统的管壳式换热器相比，体积和质量可以减少约80%[1]。除了体积较小这一优点外，由于特殊的加工工艺，PCHE在交变应力、高压条件下也具备很好的安全性和可靠性，因此尤其适用于物理性质容易发生剧烈变化的超临界流体，比如目前PCHE已逐渐成为深海浮式液化天然气装置的首选[2]；在核能领域，第四代反应堆钠冷快堆也采用PCHE作为sCO2布雷顿循环中最为推荐的换热器[3]。

在sCO2布雷顿循环中的回热器、预冷器等换热器是最重要的设备之一，研究结果[4-5]表明，换热器对于系统性能的提升具有关键作用，换热器的换热效率与稳定性将直接影响到整个发电系统的安全性和效率。比如，循环中的预冷器出口直接通向主压缩机，其换热效率将直接影响主压缩机的运行工况。因此优化换热器的传热效率，能够使sCO2在进入压缩机与透平之前得到充分的热量交换，确保循环当中压缩机和透平的工作环境满足设计要求，达到预设的性能，提高整个sCO2布雷顿循环的效率。

目前对于PCHE中的超临界二氧化碳流动换热特性，中外开展了大量研究。在实验研究方面，吴新明[6]采用实验的方法研究了sCO2在竖直圆管内的流动传热特性，提出了新的传热经验关联式；Nikitin等[7]通过实验得出了PCHE中传热与压降的经验公式；徐婷婷等[8]采用分段设计的方法建立了数学模型，研究了在不同的结构和工况下PCHE的性能；张丽娜等[9]研究了微细管中的sCO2流动特性，回归出冷却条件下竖直向上流动和竖直向下流动时的换热关联式；针对不同的流道形状，Lee等[10]对Z形流道PCHE进行了优化设计；邹智鑫等[11]既对换热器进行了热动力实验，也通过数值模拟的方法分析了换热器的热应力，热分析数值模拟与实验监测结果吻合程度较好，通过数值模拟分析评估换热器的传热特性是可行的；Ngo等[12]使用数值模拟的方法研究了sCO2在S形流道PCHE内的流动换热特性；Hu等[13]采用大涡模拟的方法对Z形流道PCHE内的流动换热特性进行了研究；然而，目前的研究集中在系统稳定运行的状态，对非稳定运行工况的PCHE中的流动换热特性研究较少。sCO2的临界温度为31.1 ℃，临界压力为7.4 MPa，相比于水来说(374 ℃， 22.1 MPa)临界条件很容易满足。但是二氧化碳在近临界点附近比热、密度都会随温度和压强产生急剧的变化，因此在非稳定运行工况下，如启动阶段或者运行状态产生波动的PCHE中，运行状态的变化会导致二氧化碳的物性产生急速变化，可能导致在某些部位脱离超临界状态，对系统的安全性和有效性产生影响。另外，通过实验的方式也很难取得非稳态工况下的换热器内部温度和压强的不均匀分布情况。因此，数值仿真作为补充手段，可以为PCHE的优化设计提供更加全面的信息。

采用流体-固体强耦合传热模型， 在每个时间步的计算中， 实时交换流体-固体交界面的传热信息。首先对设计工况下稳定运行的PCHE内部的流动和换热特性进行研究分析，并同设计性能要求进行对比，验证仿真手段对于换热过程的分析能力。随后，采用非稳定运行工况，即PCHE冷通道内的流量缓慢或者急速增加的工况下，对PCHE内部的温度变化和换热能力不均匀分布进行分析，并识别由于非稳态工况下流量变化造成的sCO2可能脱离超临界态的风险区域，为PCHE的设计优化提供参考。

另外，采用的数值仿真计算工具是开源的CFD数值仿真软件Code_Saturne[14]耦合开源的固体传热有限元分析软件Syrthes，sCO2的物性数据来自于开源材料热物理属性库CoolProp[15]，计算的几何建模及后处理可视化工具使用开源工具平台Salome的一整套开源工具链。开源软件具备了代码透明性和良好的二次开发可扩展性，通过验证采用开源工具链进行PCHE的传热过程的仿真能力，为接下来进行基于开源软件开发超临界二氧化碳循环数值分析专用工具平台，建立针对超临界二氧化碳发电设施的数字孪生系统奠定了基础。

1 计算方法

1.1 数学模型

1.1.1 流体区域的控制方程

PCHE管道内的sCO2工质流体区域由质量守恒方程、动量守恒方程和能量守恒方程描述，即

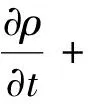
(1)

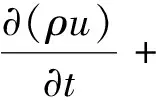
(2)

(3)

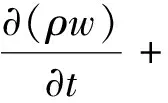
(4)

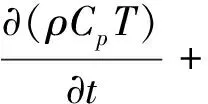
∇·(k∇T)+S

(5)

式中：ρ和u分别为流体的密度和速度矢量；u、v、w为在不同方向上的分速度；μ为分子动力黏度；SMx、SMy、SMz为不同方向上的动量源项；T为流体温度；k为流体的热导率；Cp为流体比热容；S为外部源项。

流体区域的计算采用自适应时间步长的瞬态算法，保证库伦数在5以内，速度-压强耦合求解采用SIMPLEC算法，湍流模型使用k-εLinear Production模型。

1.1.2 固体区域的控制方程

温度传递一般通过热传导、热对流和热辐射三种方式进行。在PCHE固体区域温度传递的计算中，热传导的方式占据主导地位。固体区域传热用方程描述为

(6)

式(6)中：ρs为固体区域的密度；Cps为固体材料的比热容；T是固体温度场，q为热流。

1.1.3 流体-固体计算区域的耦合

流体区域和固体区域的传热耦合是通过流体区域求解器Code_Saturne和固体区域求解器Syrthes的强耦合实现的。Code_Saturne内置Syrthes耦合传热计算接口， 分别在Code_Saturne和Syrthes求解器中进行指明流体-固体区域的交界面就可以实现流体-固体传热耦合计算。计算进行过程中，在每一个时间步的迭代内，流体区域求解器会将交界面的热流计算结果传递到固体区域求解器，并从固体区域求解器获得交界面的温度计算结果，再进行下一次的迭代循环。

2 几何模型

研究中的PCHE是sCO2再压缩布雷顿循环中的预冷器，图1为一个典型的sCO2再压缩布雷顿循环。该PCHE采用双层板排列设计，热流体采用sCO2，冷流体为液态水，两者通过逆流的方式进行换热。

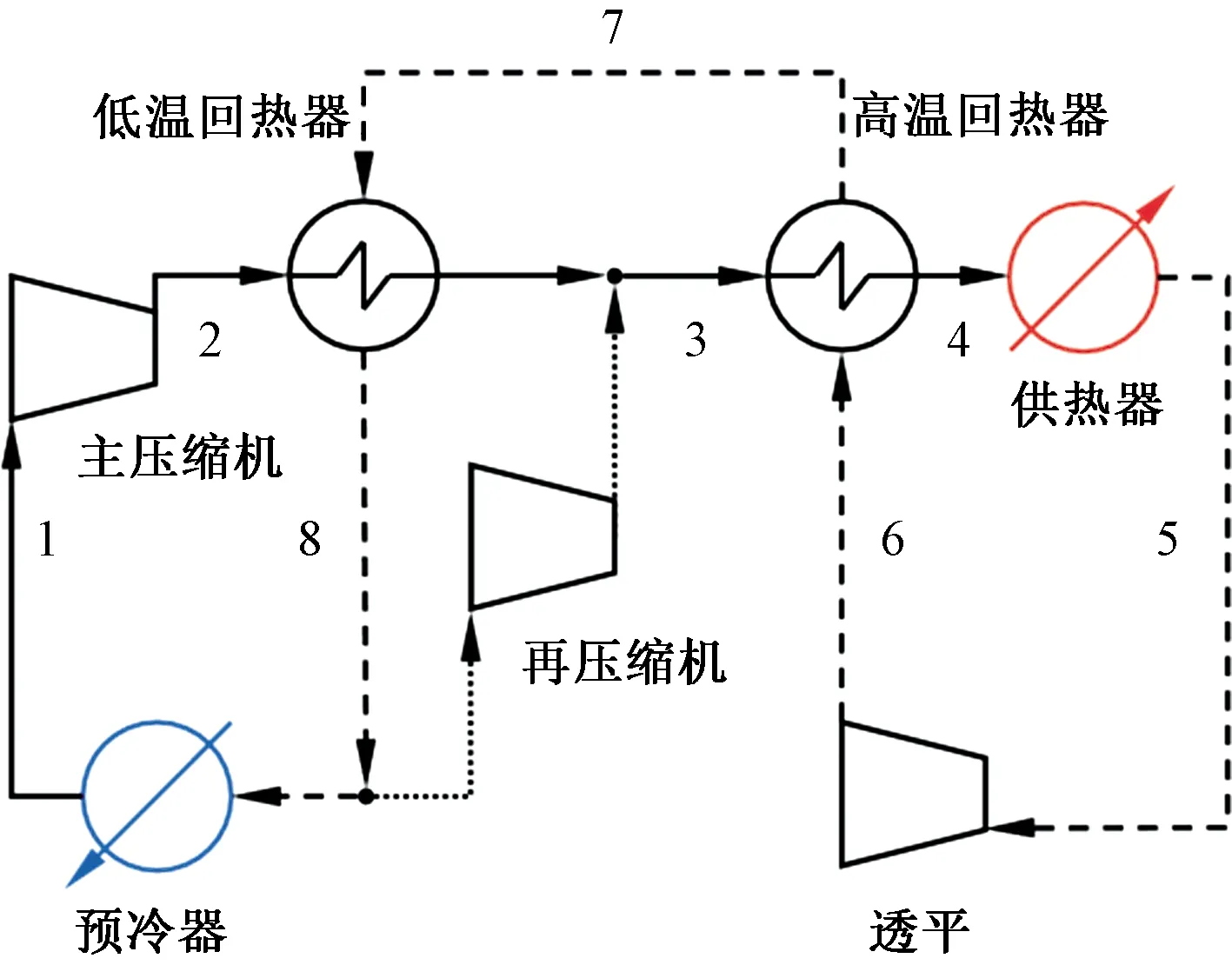
1～8表示循环中sCO2工质流动过程图1 sCO2再压缩布雷顿循环示意图Fig.1 Diagram of re-compression Brayton cycle of sCO2

PCHE总长度为0.365 64 m，其截面结构尺寸如图2所示，冷、热通道的截面直径分别为 0.994 mm 和1.017 mm 的半圆形，相邻平行冷、热通道间的壁厚为0.25 mm，具体设计参数见表1。

D为通道直径；H为换热板间壁厚；E为通道间壁厚图2 PCHE的结构示意图Fig.2 Structure diagram of PCHE

表1 PCHE的设计尺寸

整个PCHE中的冷通道数量Nc和热通道数量Nh基本相等，比例为

(7)

因此，在仿真计算中为了减少计算所需要的网格量并节省计算时间，采用5×5组的冷、热通道所覆盖的流体-固体换热区域作为计算区域(图3)， 流动传热特性分析采用位于最中心的冷、热通道的计算结果，来保证分析结果充分考虑了相邻流道之间的传热过程和相互影响。

2.1 网格划分

流体区域为结构化网格，将半圆形通道分为4个块组进行网格划分，近壁面区域满足y+值在100以内，第一层网格厚度约为0.036 mm，流体区域包含冷、热通道的总网格数目为2 820 000个。固体区域采用非结构化网格，截面上的单元长度保证在0.15 mm以下，固体区域总网格数目为2 108 700个。流体区域和固体区域的网格划分示意图如图3所示。

图3 计算区域网格划分及参数Fig.3 Diagram of mesh and generation parameters

2.2 计算工况设置

2.2.1 稳定运行工况

PCHE的设计运行工况为冷通道段进入温度为25 ℃的冷却水， 热通道端为进入温度为35 ℃的sCO2进行热量交换。稳定运行情况下的PCHE传热特性分析使用的流体区域的边界条件如表2所示。

表2 PCHE流体区域稳定运行工况边界条件设置

其中，PCHE工作流体(冷却水和sCO2)的物性通过耦合Code_Saturne和开源材料热物理属性库CoolProp进行计算给出。PCHE固体区域的材料物性设置和边界条件设置如表3所示。

表3 PCHE固体域稳态工况物性与边界条件

2.2.2 非稳定运行工况

非稳定运行工况对应的是PCHE预冷器的冷通道内的冷却水流量由小变大的情况。以稳定的充分换热的PCHE作为初始状态，随后冷通道内的质量流量在50 s内从108 kg/s升高到 245 kg/s，对应变化率为2.74 kg/s。通过非稳定运行工况下的PCHE内部的冷、热通道温度和Nusselt数的变化，分析非稳定运行情况对于PCHE整体运行状态的影响，及其可能导致sCO2偏离超临界态的风险。

2.3 传热特性的分析方法

为了分析PCHE的传热特性，计算了流体区域和固体区域进行换热的表面的努塞尔数Nu。Nu是用来衡量对流换热和热传导之间强弱的无量纲数，其定义为

(8)

式(8)中：h为对流换热系数；L为特征长度；k为流体的导热率。实际工程中，一般通过经验公式进行Nu的计算，分别采用如下两个Nu计算的经验公式： Dittus-Boelter方程和Gnielinski方程。

Dittus-Boelter方程计算Nu的形式[16]为

Nu=0.023Re4/5Prn

(9)

式(9)中：D为管道直径， 对于被加热的流体，n=0.4，对于被冷却的流体，n=0.3。Dittus-Boelter方程是工程上常用的Nu计算公式，一般适用于Re大于10 000，普兰特数Pr在0.6～160，L/D≥10的流体流动，但对于温度跨度过大的流动计算可能不够精确。并且Dittus-Boelter方程专用于光滑管道。因此，采用了更加适用的Gnielinski方程进行Nu的计算。

Gnielinski方程[17]为

(10)

式(10)中：f为Darcy摩擦因子，可以从Moody表中取得，或是从Petukhov公式中计算得

f=[0.79lnRe-1.64]-2

(11)

Gnielinski方程适用于Re在3 000～5 000 000，Pr在0.5～2 000的流动，因此更加适用于计算工况。

另外，在非稳定运行工况下，分析了sCO2可能脱离超临界态的风险大小，使用偏离超临界态指标S作为标记，S的取值方法为

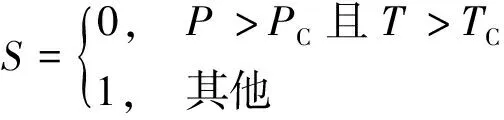
(12)

式(12)中：TC=31.1 ℃为CO2的临界温度；PC=7.4 MPa 为CO2的临界压强。通过偏离超临界态指标S的数值，可以判断哪些区域(即S=1)的温度或者压强的值已经低于或等于超临界点，有可能产生安全隐患。

3 计算结果

3.1 稳定运行工况计算结果

稳定运行工况下，首先分析不同位置的PCHE截面的温度分布云图。如图4所示，取z=0(冷通道入口)、z=L/4、z=L/2、z=3L/4以及总长度z=L(热通道入口处)的温度截面云图，可以观察到在PCHE内部的流体区域和固体区域都存在温度不均匀分布的情况。沿着流道方向，流体区域的温度随着传热过程从流道表面至中心区域逐渐升高。在每个截面上，固体区域从冷通道作为起始的截面边缘到热通道作为起始的截面边缘温度逐渐增高，流体区域靠近温度较高边缘的冷通道整体温度相比于内层的冷通道更高，而靠近温度较低边缘的最外层的热通道整体温度相比于内层的热通道更低，这是由于换热器靠近边界的管道和靠近中心区域的管道相比，只受到一侧相邻管道换热效果的影响。为了分析沿着冷、热通道方向的流动换热特征，选择最中心的冷、热通道进行分析以便充分考虑相邻管道的互相影响。取中心的冷、热通道截面上的平均温度沿着换热器流道方向的变化进行分析，结果如图5所示。可以看出，冷、热通道的温度变化平稳合理。将冷、热端的出入口温度同系统设计工况进行比较，结果如表4所示，可以得出仿真计算结果和设计工况相比，误差在5%之内。

表4 冷热两侧出入口温度与设计工况对比

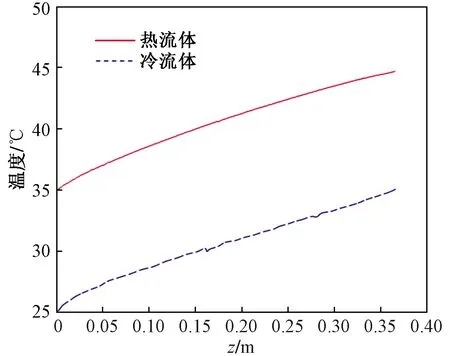
图5 PCHE温度沿换热器流道方向的变化Fig.5 Temperature elevation along the PCHE channel

通过Dittus-Boelter方程和Gnielinski方程两种常用的经验公式计算中心热通道的Nu沿着换热器流道方向的变化，结果如图6所示。可以看出，两种方法得到的Nu变化趋势是一致的。因为Gnielinski公式更加适用于所研究的非圆形管道，同时还考虑了管道粗糙度的影响，因此Gnielinski公式得到的结果数值比Dittus-Boelter公式计算的结果更大。另外，两种公式的计算结果都表明，在热通道入口处附近(z=0.9L)Nu出现了快速增长再下降的现象， 根据Chai等[18]的研究，这是由于热通道的入口效应造成的，由于通道入口处于边界层的发展区，湍动能增加有利于传热，因此在入口区域Nu快速上升，之后随着动能的逐渐损失，Nu缓慢下降。

图6 Nu沿换热器流道方向的变化Fig.6 Nusselt number elevation along the channel length

通过稳定运行工况的计算结果可知，基于开源软件工具链建立的流体-固体耦合传热模型可以得到PCHE流体区域以及固体区域的温度和传热特性的不均匀分布情况，且稳定运行得到的结果符合换热器的设计性能。

3.2 非稳定运行工况的计算结果

在实际发电过程中，会出现运行工况不稳定的阶段，如循环的启动和停止阶段，以及循环内流量发生变化等等。在这些不稳定工况中，冷、热通道的流量和温度都有可能随时间发生变化，从而导致换热器内部的传热和温度的不稳定状态。

设置冷通道流量从108 kg/s线性增加至 150 kg/s 的流量的工况，并在达到最大流量之后继续保持此流量再计算物理时间20 s。取中心的冷、热通道在z=0，z=L/4，z=L/2，z=3L/4，z=L截面上的平均温度随时间的变化，结果如图7所示。

图7 流量快速变化工况下换热器不同截面处温度随 时间的变化Fig.7 Temperature elevation along the PCHE channel in unsteady working condition

可以看出，随着冷通道流量的增加，冷通道和热通道内的温度都随之开始下降，且越靠近冷、热通道的出口，流体区域的温度下降得越快，温差也越大。在冷通道内的流量变化停止后，冷、热通道内的温度变化也几乎同时停止，可见冷通道内的流量变化对于流体区域的温度影响是瞬时的。 冷通道流量变化结束后，热通道出口处与之前的稳定运行状态相比，温度下降了2.6 ℃，而冷通道出口处与之前的稳定运行状态相比，温度下降了3.7 ℃。

使用Gnielinski方程计算沿着中心热通道内的Nu变化情况来分析冷通道流量变化对PCHE中换热特性的影响。分别计算了在冷却水流量开始变化后15、30、45、60 s时热通道内流体的Nu沿流道方向上的变化，如图8所示。

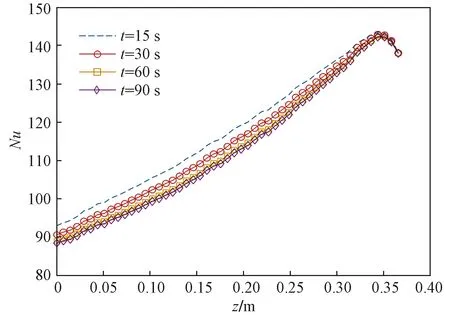
图8 非稳态工况下局部Nu随时间变化Fig.8 Nusselt number elevation along the PCHE channel length in unsteady working condition

可以看到，Nu曲线形状趋势相同。随着冷通道内的流量随时间增加，热通道内的Nu整体略有降低但变化幅度小于1%，基本可以忽略，因此冷通道内的流量大小变化对于此工况下的PCHE的换热特性并没有太大影响。

为了分析非稳态运行中热通道内的二氧化碳工质是否有偏离超临界态的风险，采用上一章定义的偏离临界态风险指标S，对非稳态工况进行分析，所得结果如图9所示。在初始状态下，全部的二氧化碳都处于超临界态, 随着冷通道内的流量增大，整体PCHE的温度下降，热通道内的二氧化碳偏离超临界态的风险区域从最靠近温度偏低的边缘处的热通道出口处逐渐扩大至内部管道区域。

图9 非稳态工况下二氧化碳脱离超临界态风险指标S 随时间的变化Fig.9 CO2 emissions from supercritical risk index S elevation by time in unsteady working condition

通过非稳态运行工况的仿真分析结果可以得出，在冷、热通道流量波动的情况下，由于PCHE内部存在温度分布不均匀的情况，位于最边缘的热通道出口附近是温度最低区域，如本文中研究的预冷器，其设计运行工况本身就接近二氧化碳的超临界温度，则非常容易在此区域出现温度过低从而导致此处的二氧化碳工质偏离超临界态，对整个系统造成安全隐患。

4 结论

通过流体-固体区域强耦合传热方法，采用完全开源的数值仿真工具链，对sCO2再压缩布雷顿循环中的PCHE预冷器的流动传热特性进行了分析。结果表明，使用开源通用流体力学软件Code_Saturne耦合Srythes有限元固体传热求解器以及CoolProp热物理材料库对使用sCO2作为工质的布雷顿循环进行数值模拟是非常适用的。在稳定的设计工况运行条件下，仿真模拟结果符合给定的设计工况。同时，可以观察到PCHE内部流体区域以及固体区域的温度以及换热效率的不均匀分布情况。在非稳定工况运行条件下，即冷通道内流量变化的情况下，因为流量变化导致的冷、热通道的温度变化是瞬时的，冷通道的流量波动会直接造成整个系统的温度波动，并因此产生可能偏离超临界态的二氧化碳流体区域，尤其是在靠近PCHE边缘附近以及出口附近的热通道内。由于PCHE预冷器的出口将会跟循环中的主压缩机进行连接，一旦产生偏离超临界态的情况，会直接对压缩机的正常运行产生影响，因此需要在设计阶段考虑到冷、热通道内的流量波动以及PCHE内部的温度分布不均匀性，从而保证整个布雷顿循环的运行效率和运行安全。数值仿真手段为PCHE的设计和运维优化提供了更加全面的信息，开源仿真工具链的验证，为基于开源仿真工具所提供的二次开发可扩展性，在实际工程应用中建立更加复杂和完整的超临界二氧化碳循环数值模型和以超临界二氧化碳为工质的机械设备的数字孪生，从而更好地辅助设计、生产和运维的设备全生命周期提供了可能性。