巧用楼层法深入浅出认识正方体堆叠问题的方法探析

张超

摘 要：小学生的空间观念和空间想象力相对较差，正处于不断培养和发展的阶段，所以在图形与几何模块的学习过程中会比较困难。文章以正方体堆叠问题为例，介绍一种“楼层法”，将正方体类比成楼房，通过数楼层数即可判断出小正方体个数。这个方法可以帮助学生更好地理解正方体堆叠问题。通过不断的观察、分析和想象，逐步在学生的认知里培养空间观念和想象力，为今后数学的学习打好基础。

关键词：正方体堆叠;小学数学;空间观念

正方体堆叠问题在考试题中频频出现，空间想象力欠缺的小学生在面对这类题时很难形成空间立体图形，而教师在教学中多半是让学生自己去想象，缺少对空间观念的培养。文章将介绍一种分析方法，即“楼层法”。该方法是通过改变学生观察的角度，以“排”为单位，从纵向来观察，在正方体的顶部进行观察和想象，这种方法不会忽略无法观察到的正方体，可以准确快速地判断出堆叠的小正方体的个数，让学生更好地理解空间图形，也为教师对学生空间想象力的培养提供了新的方法。

一、 如何使用“楼层法”解决正方体堆叠问题

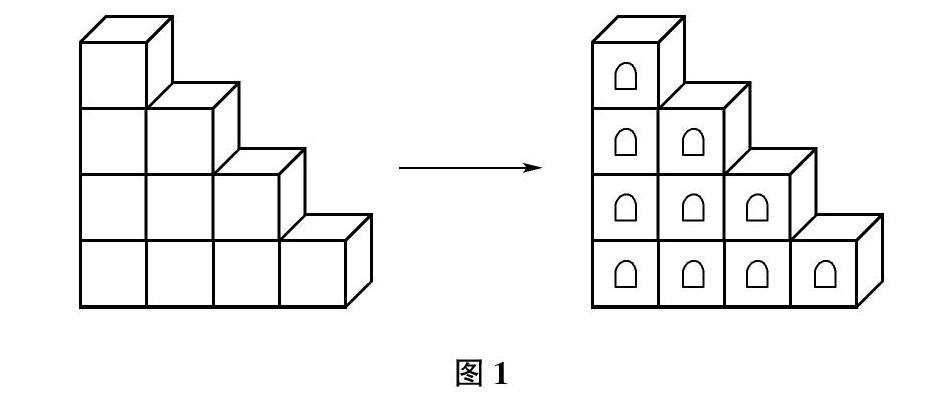
“楼层法”顾名思义，我们将每列的正方体类比成单元楼（图1），从左边数起分别为：一单元，二单元，三单元和四单元。每一个单元楼的楼层数是不同的，分别是：4层、3层、2层和1层。那么这个正方体堆叠图形中含有的小正方体个数就是4+3+2+1=10（个）。这就是用“楼层法”解决正方体堆叠问题。正方体可以类比成楼房，是因为正方体堆叠与盖房子原理是一样，正方体堆叠是从下面开始，一个一个小正方体往上堆，而楼房也是同样的，从最底层开始，一层一层地往上盖，因此将正方体类比成楼房是非常合理的;此外，楼房在生活中随处可见，将正方体类比成楼房的方法，与生活实际相结合，学生可以更好地理解立体图形，有助于空间观念的培养。

二、 利用“楼层法”求解正方体堆叠问题

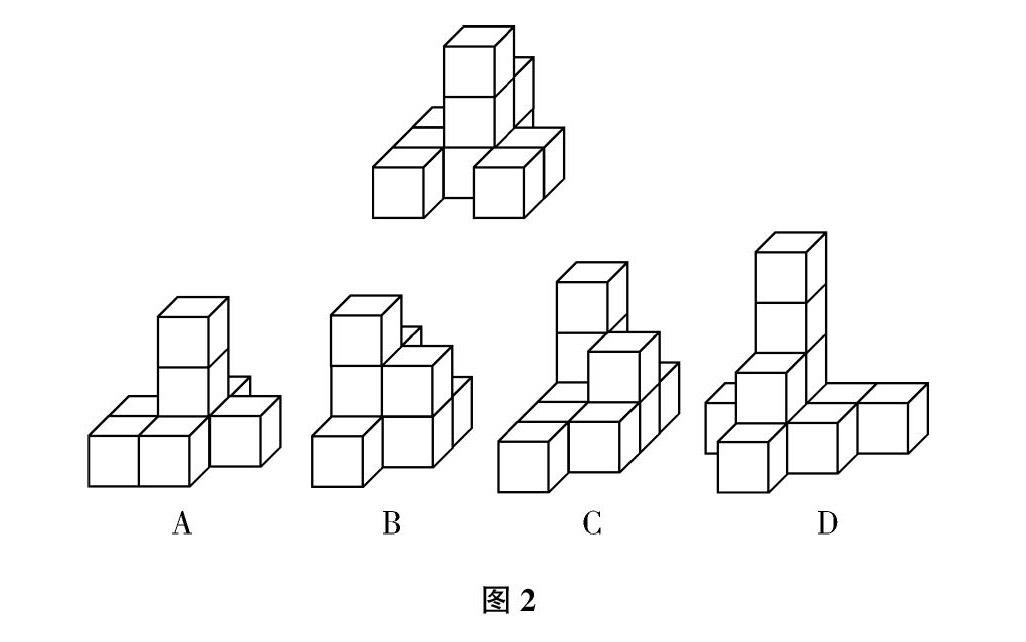
【例1】 如图2，右侧的立体图中哪个与左侧的立体图中的小正方体个数相同？

解析：左侧立体图中小正方体的个数：左侧一排中的每一列都是由1层组成，中间排是有2列组成，每列分别是3层和2层，右侧共两列，每列只有1层，故左侧立方体图中小正方体的个数为：1+1+1+3+2+1+1=10（个）。接下来需要从右侧四个图形中找到由10个小正方体组成的图形。

选项A：左侧中有1+1=2（个），即2个小正方体。中间一排在数层数时要注意，前面是1层，中间是3层，后面还有1层，很多学生可能会将这个小正方体忽略掉。右侧只有1层，因此，A选项中小正方体个数有2+1+3+1+1=8（个），与左侧图形数目不同，不符合题意。当我们对于这种方法熟练后，可以直接写出每列的楼层数，即小正方体个数，直接加和求解。选项B：1+3+2+2+1=9（个）。选项C：1+1+1+3+1+2+1=10（个）。与左侧图形中小正方体个数相同。选项D中小正方体个数为：1+1+2+4+1+1+1=11（个），与题目中的要求不符。因此答案为C。

分析：这一组立体图较为复杂，有很多隐藏起来的正方形，如果直接去数小正方体个数，很容易丢掉某个小正方体，尤其是选项B，利用“楼层法”完全避免了这种错误，只要是在直观图中看到的，就可以根据层数数出小正方体的个数。

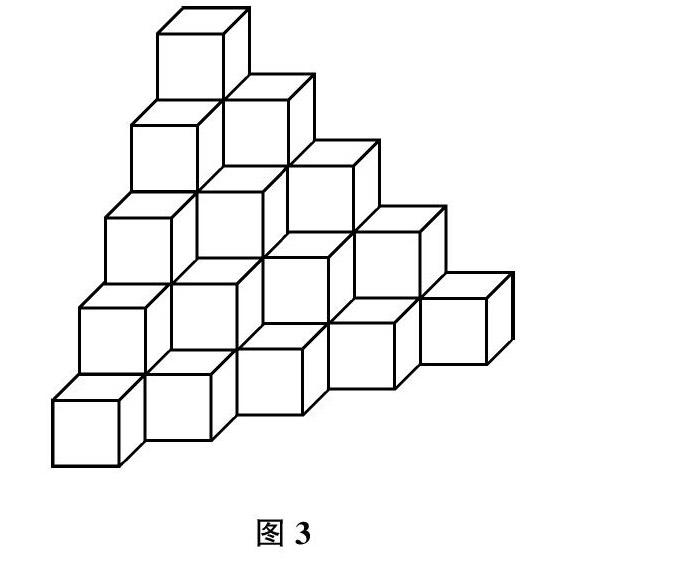
【例2】 图3中立体图形至少由    个小正方体组成的？

解析：【解法1】利用简单的“楼层法”数出每一列的小正方体个数。左侧一排是由1+2+3+4+5=15（个）;第二排：1+2+3+4=10（个）;第三排：1+2+3=6（个）;第四排有3个，最后一排只有1个。最后将每一排小正方体个数相加：15+10+6+3+1=35（个）。因此，图3中的立体图形至少由35个小正方体组成的。

【解法2】利用“分层法”从最高层或者从最底层数起，数出每层含有的小正方体个数，然后加和。仔细观察发现图3中的立方体在堆叠时有一定的规律性，即：下层小正方体的个数是在上层正方体的基础上依次增加2个、3个、4个、5个小正方体。例如：第2层小正方体的个数是在第1层1个正方体的基础上加上2个小正方体，即1+2=3（个）;第3层是在第2层3个的基础上加上3个小正方体，即1+2+3=6（个）;以此类推，第4层小正方体的个数为：1+2+3+4=10（个）;第5层小正方体的个数有：1+2+3+4+5=15（个）。最后将每一层的小正方体数加起来为：1+3+6+10+15=35（个）。与解法1的答案相同。

分析：比较两种解题方法，解法2是先通过观察和分析发现被压的小正方体的个数与上一层的小正方体个数相同，每多加一层，小正方体的个数就在上层小正方体的个数的基础上增加该层的层数个。这种方法需要学生仔细观察，不仅需要空间思维能力还需要学生的总结归纳和分析能力。而“楼层法”则相对简单，通过比较楼层的高低，我们能够清晰地观察到每一列所含的小正方体的个数，不会因为遮挡和堆叠而漏掉某个小正方体。

拓展：教师在进行解法2的讲解时，可以增设一问：如果依规律摆下去，当摆到第10层时，立体图形是由    个小正方体组成的？依照規律，第几层就是在上一层的基础上加上该层层数个小正方体，所以第10层的小正方体个数为第9层的小正方体个数加10。即：1+（1+2）+（1+2+3）+（1+2+3+4）+…+（1+2+3+4+5+6+7+8+9+10）=220（个）。这一问的增设，既可以加深学生对解法2的理解，又可以调动学生探究未知的积极性，让学生更好地融入课堂的学习中。

三、 正方体堆叠与补全正方体的混合求解

【例3】 如图4所示，要想把下面左边的立体图形补全成为右边的大的完整的正方体，至少还需要多少个小正方体呢？

解析：想要知道还需要多少个小正方体，首先需要确定右侧的大正方体（我们将完整的大正方体定义为“整体”）和左侧的残缺的立体图（我们将残缺的立体图定义为“部分”）中含有的小正方体个数，再利用“整体的数量-部分的数量=需要补充的数量”的方法，求解出还需要多少个小正方体。根据“楼层法”可以直接判断出“部分”图形中含1+2+3+1+2+2+1+1+1=14（个）小正方体。右侧“整体”的立体图形中总共有3+3+3+3+3+3+3+3+3=27（个）小正方体。因此，根据“整体的数量-部分的数量=需要补充的数量”计算，故至少还需要27-14=13（个）小正方体，可以将左边的立体图形补全成为右边的大的完整的正方体。答案为13个。