Nonclassical Lie symmetry and conservation laws of the nonlinear timefractional Korteweg–de Vries equation

Mir Sajjad Hashemi,Ali Haji-Badali,Farzaneh Alizadeh and Mustafa Inc

1 Department of Mathematics,Basic Science Faculty,University of Bonab,Bonab,Box 55513-95133,Iran

2 Department of Computer Engineering,Biruni University,Istanbul,Turkey

3 Department of Mathematics,Science Faculty,Firat University,23119 Elazig,Turkey

4 Department of Medical Research,China Medical University Hospital,China Medical University,Taichung,Taiwan,China

Abstract In this paper,we use the symmetry of the Lie group analysis as one of the powerful tools that deals with the wide class of fractional order differential equations in the Riemann–Liouville concept.In this study,first,we employ the classical and nonclassical Lie symmetries (LS) to acquire similarity reductions of the nonlinear fractional far field Korteweg–de Vries (KdV)equation,and second,we find the related exact solutions for the derived generators.Finally,according to the LS generators acquired,we construct conservation laws for related classical and nonclassical vector fields of the fractional far field KdV equation.

Keywords: fractional equation,Lie symmetry analysis,classical and non-classical symmetries

1.Introduction

Hyperelastic materials such as rubber and rubber-like materials have great properties.For instance,some of these properties are the large deformation,high elasticity,and typical characteristics of nonlinearity.Their products are used in transportation,aerospace,petrochemicals,etc frequently.These materials and their products are usually used in specific environments,and all encounter the problems of instability,deformation,destruction,etc.Hence,the dynamic stability of these materials and structures has always been considered[1–3].Since then,a lot of remarkable work has been done.For hyperelastic materials the main aspects of nonlinear elastodynamics can be found in Chou-Wang et al [4–9].Cohen et al [10] studied the propagation of nonlinear traveling waves in a cylindrical rod composed of a class of compressible Mooney–Rivlin materials and obtained a system of nonlinear evolution equations for describing the symmetrical motion of the rod.By applying the reduced perturbation method,the authors reduced the governing equation to the Korteweg–de Vries (KdV) equation and proved that there exist finite-amplitude waves [11].

Lie group transformations were first put forward by Sophus Lie,who was an influential Norwegian mathematician in the early 19th century.These transformations play a fundamental role in the analysis of different kind of differential equations[12–14].The classical Lie symmetry method (LSM) is utilized for fractional differential equations in[15–19].Various branches of LSM are introduced in order to find additional generators.Some of the most important ones are nonclassical Lie symmetries[20–23],λ- symmetries [24–26],and so on.

Tian [27] efficiently applied Lie symmetry analysis to obtain exact solutions for a fourth-order nonlinear generalized Boussinesq water wave equation.An interesting application of Lie symmetry analysis to solve the time-fractional Fordy–Gibbons equation has been presented by Feng et al[28].Mao et al [29] used the Lie group method to extract analytical solutions for the (2 + 1)-dimensional chiral nonlinear Schrödinger equation.They employed this method to find the optimal system of the equation.Furthermore,in their work,the similarity reductions were examined based upon the obtained optimal system.Recently,Wang et al [30] studied the KdV equation in (2+1) dimensions by employing Bell’s polynomial to obtain a bilinear representation of the equation.They also constructed the general lump solutions of the equation by considering the resulting bilinear form.Some new analytical solutions of the extended Zakharov–Kuznetsov equation have been evaluated by Wael et al [31] via symmetry reduction.This equation was employed to model the nonlinear plasma dust acoustic waves in a magnetized dusty plasma.Jahangeer et al [32,33] employed the Lie symmetry analysis technique as the most effective method to obtain some exact explicit solutions for time-fractional partial differential equations.It is necessary to note that they used some similarity reductions for the governing equations,which convert them to ordinary differential equations.Fractional calculus theory has received much attention from researchers and scientists in applied mathematics and physics because of its remarkable properties to accurately describe different abnormal physical events and complex processes in engineering and applied science such that classical calculations were insufficient to explain them [34–37].To investigate fractional calculation theory,several abnormal events have been sampled through integral or functional differential equations in the real world.There is an essential fundamental difference between differential operators of integer order and the Riemann–Liouville (RL) fractional derivatives; the former are local operators,the latter are not.In recent centuries,the theory of fractional calculus and providing various fractional order derivative and integral operators have gained considerable importance among researchers.In fact,they found the fractional order operators to be a powerful instrument which can be used to perform more accurate descriptions of some nonlocal phenomena than the classical integer-order models in the different fields of applied science and engineering.Now,the well-known fields of fractional calculus include control,porous media,electrical networks,electrochemistry,signal processing,and spread of disease [36,38–40].

We investigate the Lie symmetries of the valid asymptotic far field equation for axis symmetry longitudinal strain waves passing through a cylindrical rod obtained by using the reduction perturbation method in [11].The mentioned cylindrical rod is composed of general noncompressible materials such as isotropic rods that are nonlinear in the real world.This extraction was performed by expanding radial and axial displacement asymptotically in [11].The longitudinal strain waves explained by the KdV equation of the far field [11] are given by the following equation:

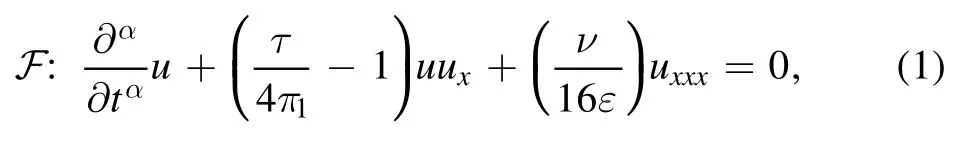
whereτ,π1andν,εare material and structural coefficients,respectively.Assume that in this equationandTherefore,β1is an arbitrary value and β2is not negative.In the cylindrical rod,the structural constants and combined material are introduced as general incompressible materials,and the waves that travel through such rods are longitudinal strain waves.Equation (1) is obtained by applying the reductive perturbation method in [11].Lou's direct method and symmetry transformation were used to find the exact solution of equation (1) in [41].The problems extracted from solid theory are often explained as nonlinear partial differential equations,and various numerical and analytical methods have been employed to study and solve for the unknowns.Here we intend to obtain the exact solutions of equation (1) with one of the most powerful analytical methods(the Lie symmetry analysis method,LSAM).

2.Preliminaries

In this part,we present some basic definitions for the fractional operators and LSAM of fractional partial differential equations(FPDEs).We advise readers who wish to read more on these definitions and other properties of fractional differentiation to see [34–36].

2.1.Fractional operators

Definition 1.RL derivative operator of order α,which is described in [36] as:

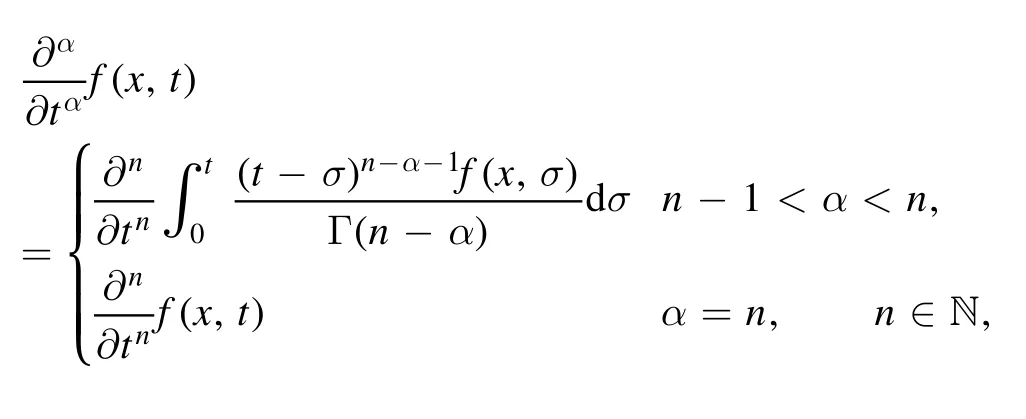
where Γ(·) denotes the well-known gamma function.

Definition 2.Erdélyi–Kober fractional integral operators for F(ζ)

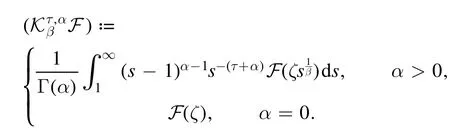
Definition 3.Erdélyi–Kober fractional derivative operators forF(ζ)

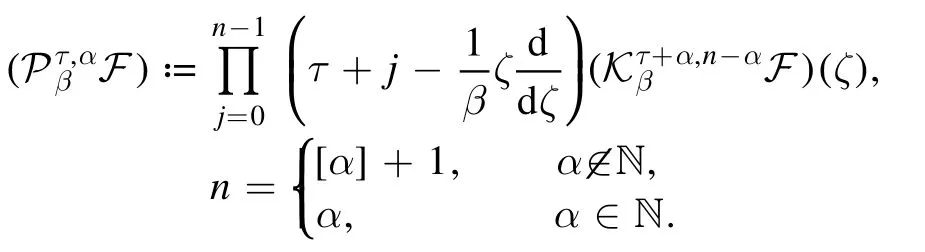
2.2.LSAM for FPDEs

The following FPDE of orderα∈ (0,1) is considered as:

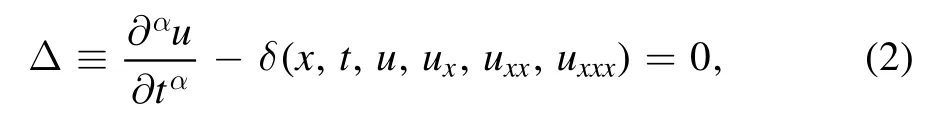
where x,t are independent variables,and u is dependent on x,t.

Suppose that equation(31)is invariant with respect to the following one parameter Lie symmetry transformations:

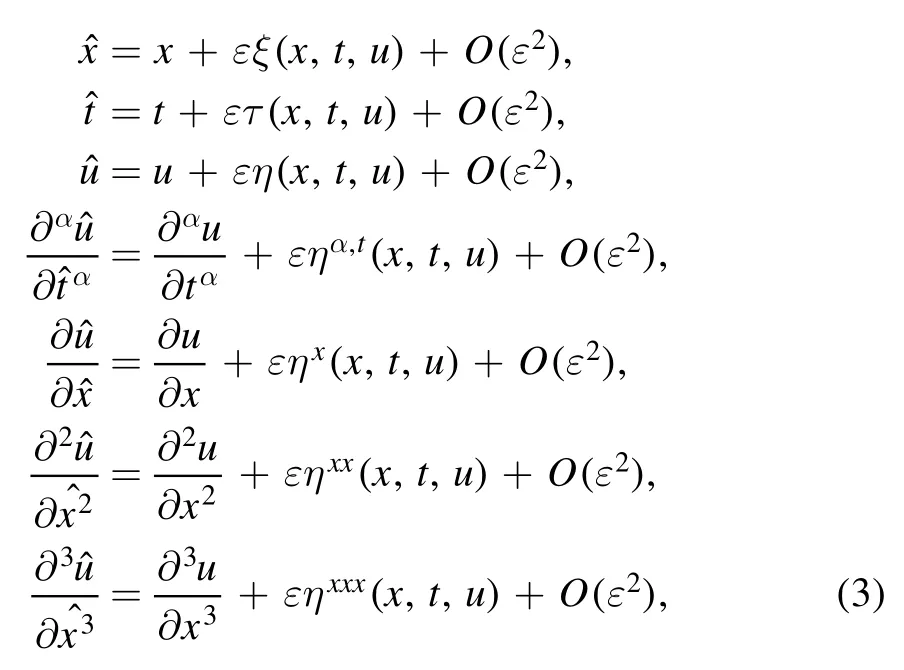
where the group parameter is shown by ε,and its corresponding infinitesimal generator is

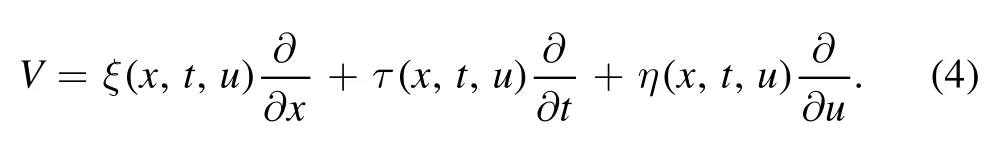
This vector field must create a symmetry of (31) iff the following is true in invariance conditions:

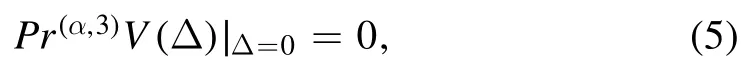
where 3 show the highest integer orders of extended infinitesimals in equation(2),and it is worth noting that the extended operator of fractional prolongationPr(α,3)Vis introduced by [15]:

whereη x,ηxxandηxxxrepresent integer-order extended infinitesimals which are defined as:

and the operator of the total derivative along x,i.e,Dx,is:

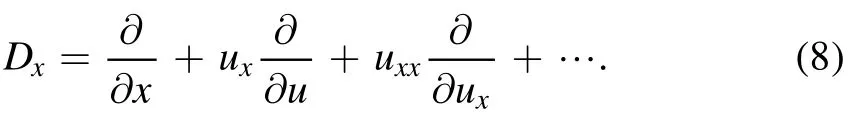
Moreover,the α-order extended infinitesimal operatorηα,tis(see[42,43])

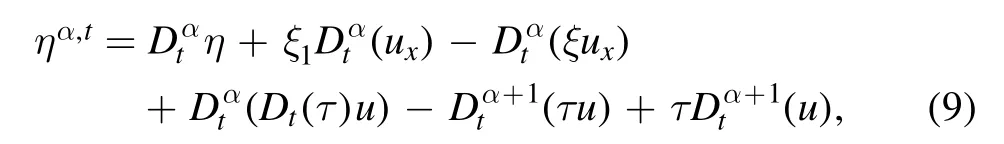
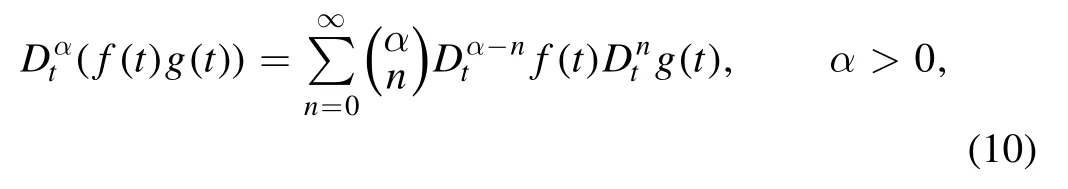
where

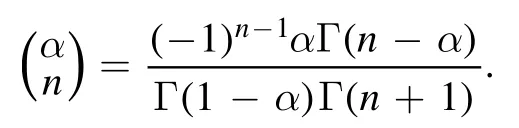
Using equation (10),equation (9) can be written as

We want to be reminded that the generalization of the wellknown chain rule for a composite function [34] is given by

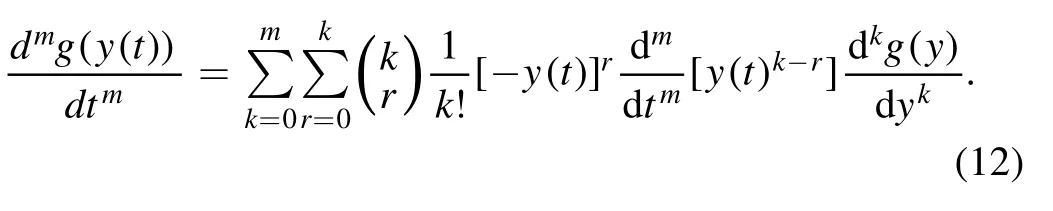
Using the chain rule(12)along with the generalized Leibnitz rule(10),it is assumed that f(t) = 1,and we can write the first termon the right hand side of (11) as

where

Then,the α-order extension of infinitesimalηα,tcan be obtained as

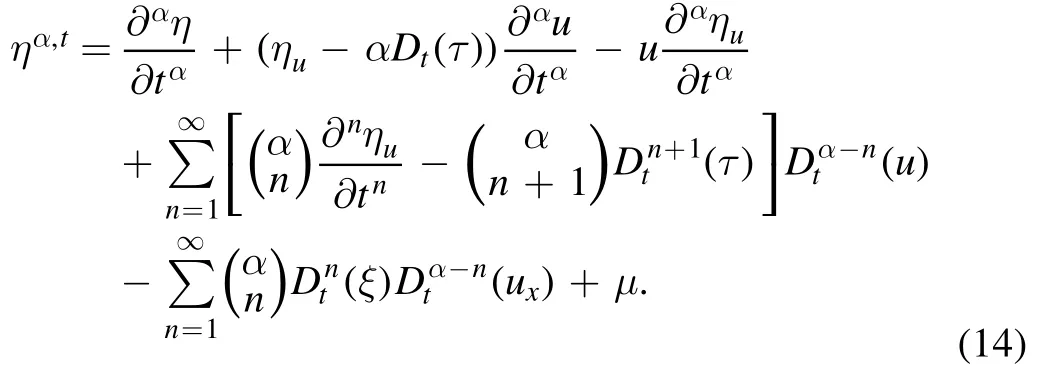
Furthermore,since η is linear wrt variable u,then derivativesforn≥ 2 are vanished and immediately we conclude that μ = 0.By substituting the above equations in(6)and solving the determining equations we obtain the classical symmetry generators by comparing the coeffciients ofu x,u xx,uxt,….In this method we lose some invariance.Bluman and Cole presented the nonclassical method of reduction to obtain new exact solutions of the heat equation[44].The main idea of this method is based on inserting an invariant surface condition such that combination of the original determining equation and this condition yield a nonlinear determining equation for infinitesimals.We can solve this new nonlinear determining equation for infinitesimals too and get more symmetries.

To obtain the solutions u = u(x,t)of equation(2)which are invariant under the group transformations (3),we must consider

For the nonclassical method,we are looking for invariability of the two following equations simultaneously:

In order that equation(17)is satisfied for every ξ,τ and η,it is sufficient that Ω = 0.Therefore,we consider only the invariant surface condition

with equation(16).There is no loss of generality in assuming ξ = 1 and ξ = 0.When ξ = 1 we have two conditions:τ = 0 and τu= 0.In the case ξ = 0,where τ is opposite to zero,the acquired system of determining equations is usually complex and difficult to calculate.

3.Implementation of LSAM for time-fractional KdV equation

The time-fractional far field KdV equation is in the following form:

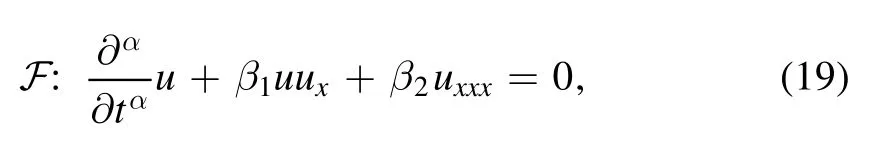
3.1.Classical symmetries

If we apply prolongation of the fractional vector field to the this equation,we obtain

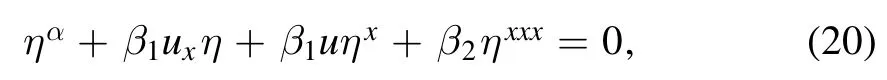
and by substituting (7) and (14) in (20) and solving the determining equations we acquire the following symmetry generators:

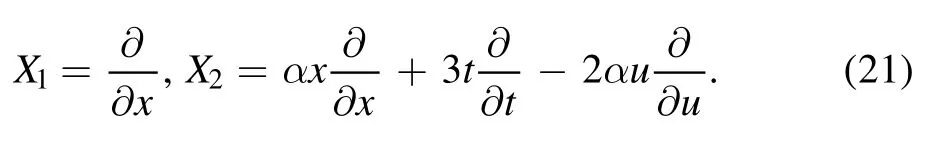
The invariant solution of vector field X1isu(x,t) =f(t),and then equation(19)is reduced to the following time-fractional ODE equation:

Hence,the exact solution of equation(19)isu(x,t) =c1tα-1.

According to the vector field X2we have the following invariant solution for equation (19):

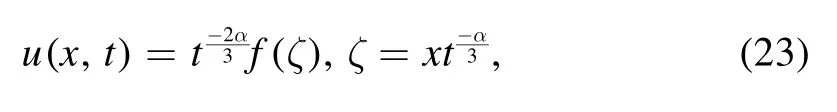
and by using the above transformation and substituting in equation (19) we obtain the fractional ODE

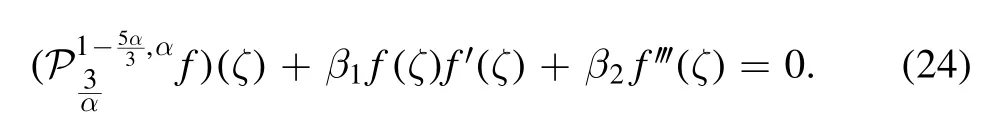
We can find the exact solution of(24)by using a power series method.Let

then,

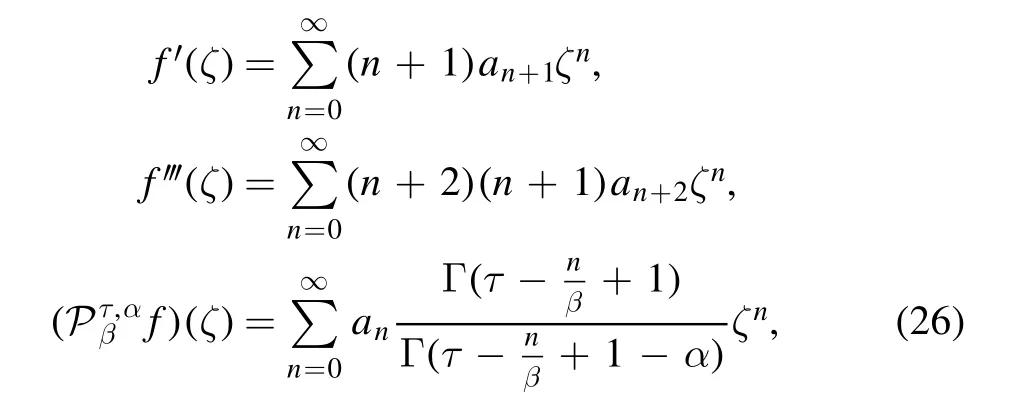
and substituting the above relation in (24) we have

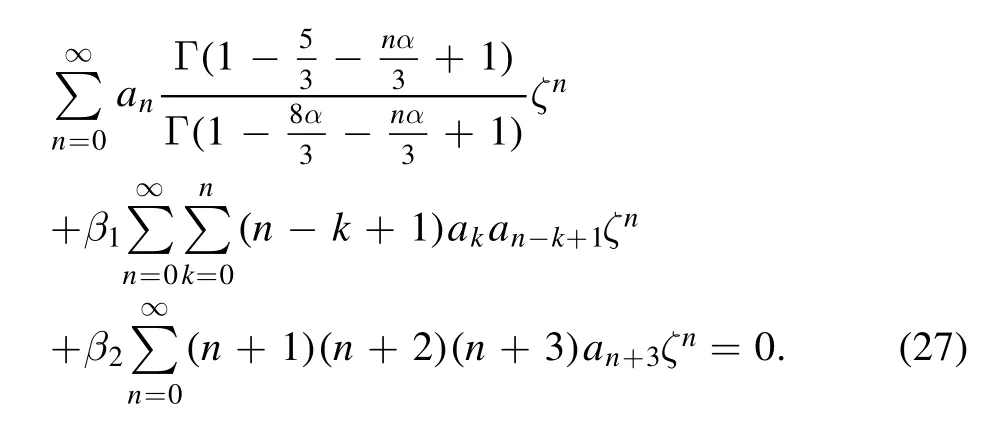
According to equation (27),for n ≥ 0 we have the following recursive relation:

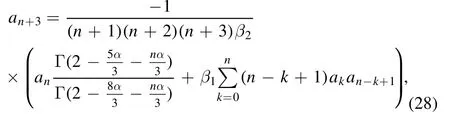
anda0,a1and a2are arbitrary constants.According to (23),the exact solution of equation (19) is

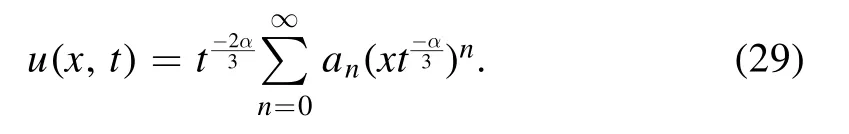
In order to illustrate the related plots of the obtained exact solution (29),we truncate its series with N = 24.Figure 1 shows the plots of u(x,t)for a0= 1,a1= 0.5,a2= 0.25 and β1= β2 = 1.Figure 1(a) shows the convergence properties of the obtained exact solutions to the exact solution of the integer-order KdV equation when α tends to 1.

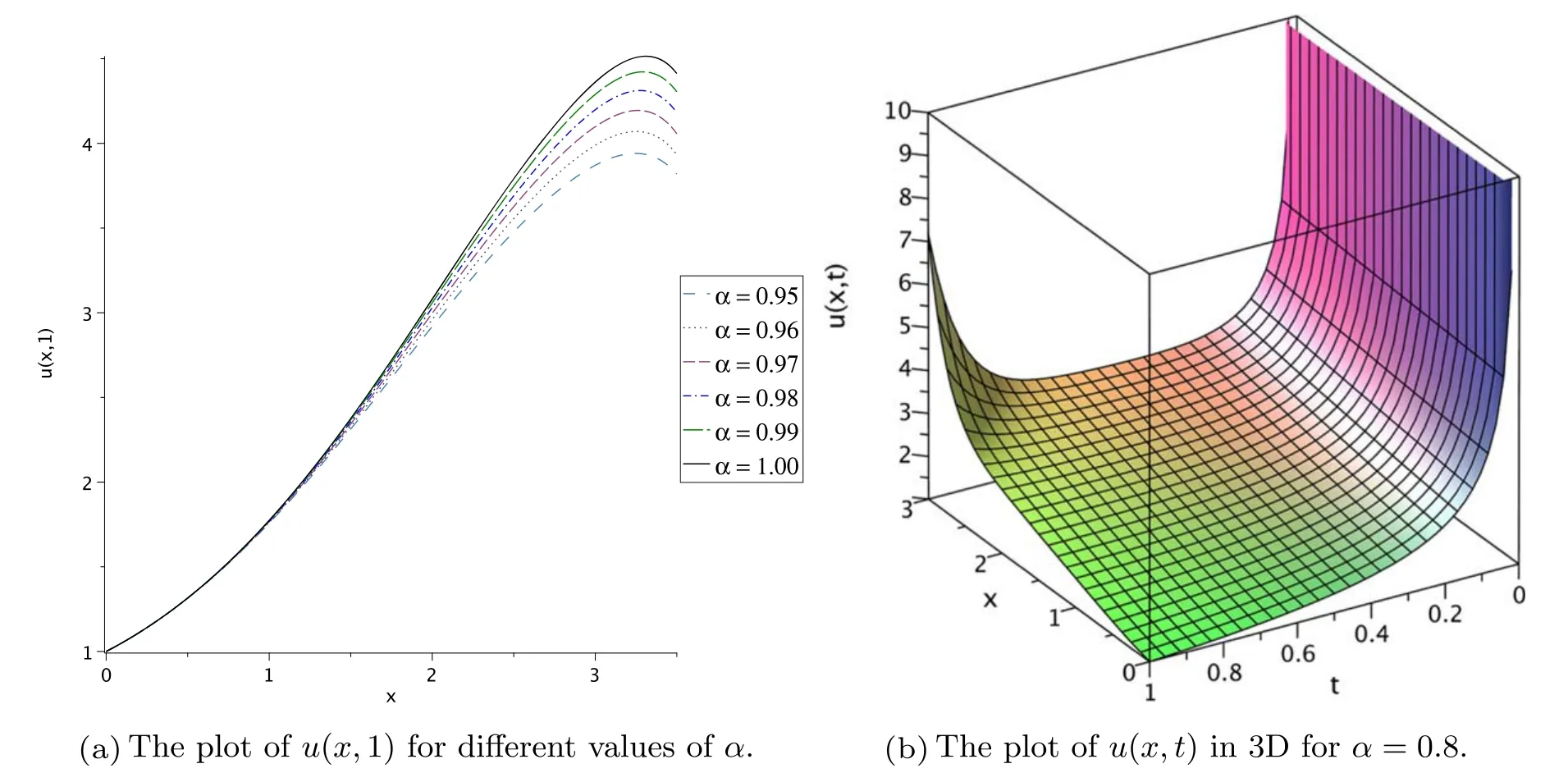
Figure 1.Related plots of the exact solutions of (29) obtained by the classical generator of X2 for different values of α in 2D and 3D.

3.2.Non-classical symmetries

In this case for ξ = 1 and τ = 0 we have

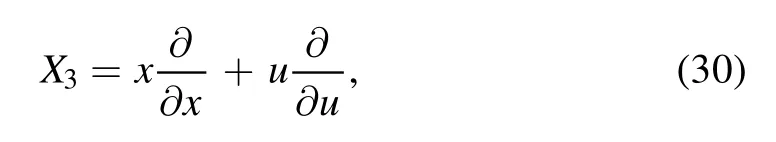
and the invariant solution according to this vector field is

Substituting (31) into equation (31) yields

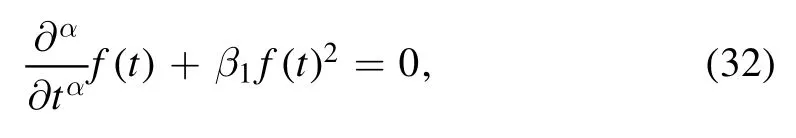
and therefore,the solution of (32) is

so the exact solution of (19) is as follows:

Figure 2 shows the plot of u(x,t) for β1= β2 = 1 and α = 0.75 in 3D.

Figure 2.Related plot of the exact solution of (34) obtained by the nonclassical generator of X3 for α = 0.75 in 3D.

For ξ = 1,τ≠0 and τu= 0 we have the following vector fields:

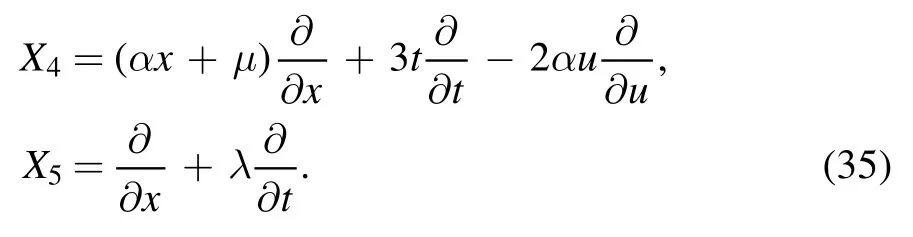
By the infinitesimal generator X4,we obtain

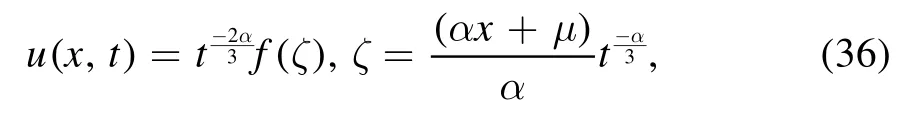
and then,equation (19) can be reduced to the following fractional ODE:

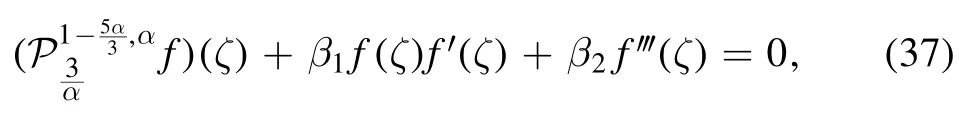
so in the same manner used for the infinitesimal generator X2,we have the following exact solution:

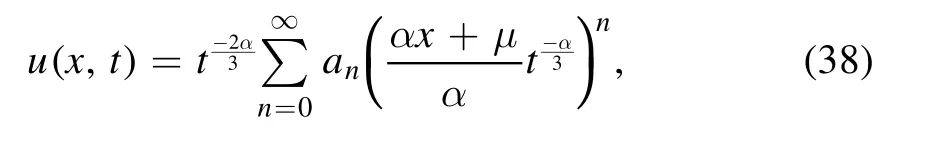
where μ is a constant.

In order to illustrate the related plots of the computed exact solution (38),we truncate its series with N = 24.Figure 3 shows the plots of u(x,t) for a0= 1,a1= 0.5,a2= 0.25,μ = 0.5 and β1= β2 = 1.Figure 3(a)shows the convergence properties of the obtained exact solutions to the exact solution of the integer-order KdV equation when α approaches 1.

Figure 3.Related plots of the exact solutions of (38) obtained by the nonclassical generator of X4 for different values of α in 2D and 3D.

The invariant solution of the infinitesimal generator X5

can reduce the equation (19) to the time-fractional ODE

and it is not easy to find the exact solution of this equation.

4.Conservation laws of the KdV equation

In this part,we turn attention to the nonlinear self-adjointness[45] and new conservation laws (cl) theorem that was first used to construct the cl by Ibragimov in [46].This theorem uses the LS to find conserved vectors.Here we intend to construct cl for (19) according to this method.The cl for equation (19) is given by

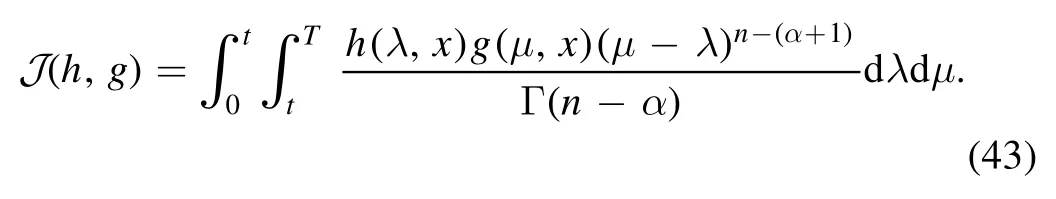
The formal Lagrangian for (19) is given by

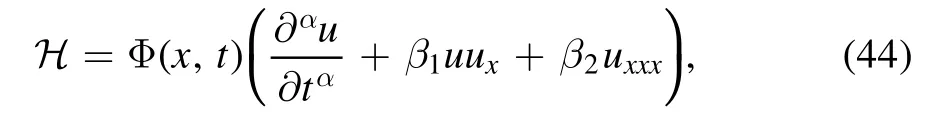
where Φ(x,t) = Ψ(x,t,u) is a new dependent variable and the adjoint equations of the fractional KdV equation can be specified as follows:

where the Euler–Lagrange operators are given by

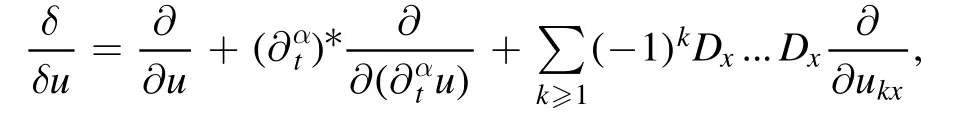
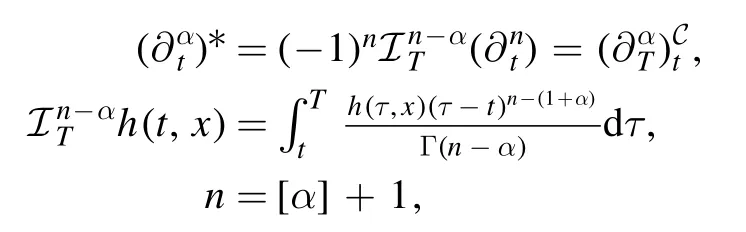
If we have the following relation for the time-fractional nonlinear equation(44),then we can say that equation(19)is self-adjoint:

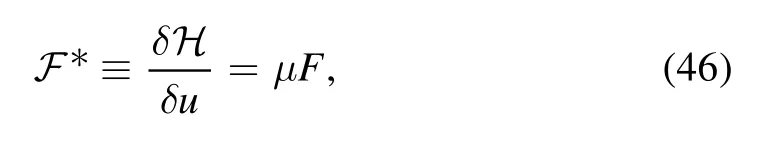
where μ remains to be determined.Thus,we can write the nonlinear self-adjoint condition (46) as follows:

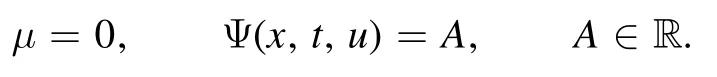
Hence,if we suppose A = 1,then

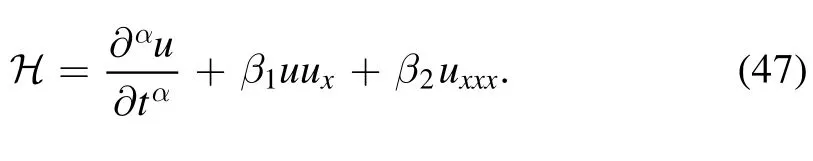
According to the above analysis and Lie symmetry generator,we consider the conserved vectors for classical and nonclassical generators of the time-fractional far field KdV equation.We have the following cases for classical generators:

Case 1:Here for the first classical generator X1,the respective Lie characteristic function is

Substituting (48) into (42) yields the conserved vector as follows:

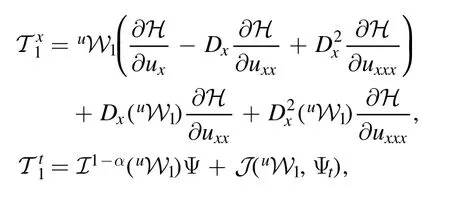
then

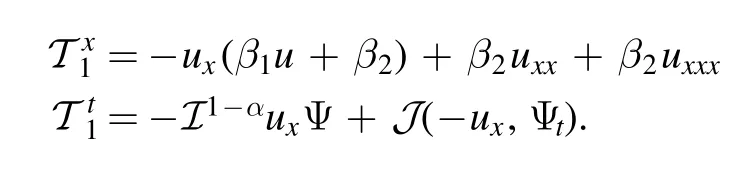
Case 2:For the generatorthe respective Lie characteristic function is obtained by

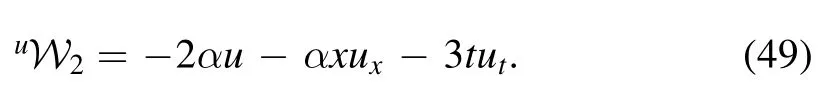
Substituting (49) into (42) yields

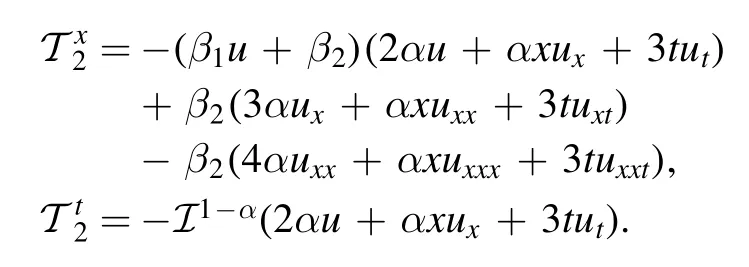
For nonclassical generators:

Case 3:For ξ = 1 and τ = 0 we haveand the respective Lie characteristic function is obtained by

Hence,substituting(50)into(42)yields the conserved vector as follows:

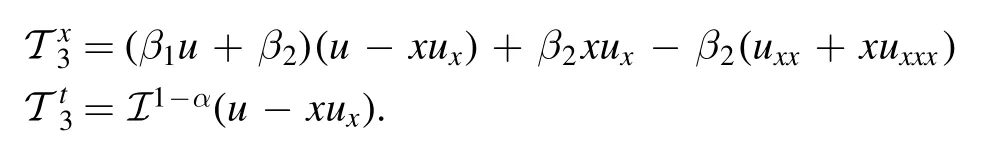
Case 4:For ξ = 1 andτ≠0,we haveX4=(αx+The respective Lie characteristic function is obtained by

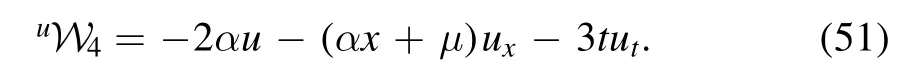
The corresponding conserved vectors are

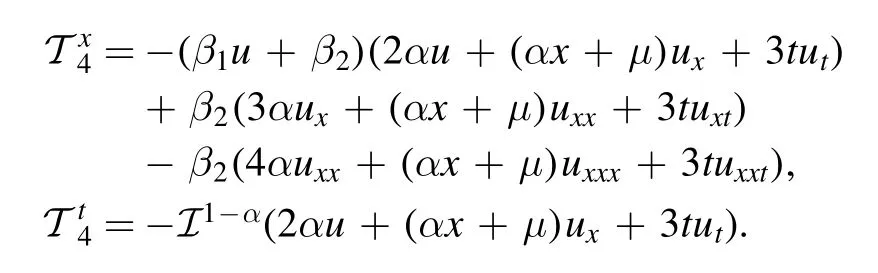
Case 5:The respective Lie characteristic function foris obtained by

The corresponding conserved vectors are

5.Conclusion

In this work,we mainly study the classical Lie symmetry,nonclassical Lie symmetry and conservation laws of the nonlinear time-fractional KdV equation.We use the symmetry of the Lie group analysis for the nonlinear timefractional far field KdV equation and employ classical and nonclassical Lie symmetry to acquire similarity reductions of this equation according to the obtained vector fields and the corresponding invariant solutions.We also find the related exact solutions by some methods like the power series method for the derived generators.From figures 1 and 3,one may find that our obtained solutions in both the classical and nonclassical cases have convergence behavior.Finally,according to the LS generators acquired,we construct conservation laws for related classical and nonclassical vector fields of the mentioned equation.From these findings,we conclude that the presented method might become a promising one in finding the analytical solutions of different kinds of fractional partial differential equations.

Acknowledgments

The authors would like to thank the respected referees for their valuable comments that led to improvement of this paper.

ORCID iDs