Grüneisen ratio quest for self-duality of quantum criticality in a spin-1/2 XY chain with Dzyaloshinskii–Moriya interaction

Lin-Jie Ding (丁林杰)and Yuan Zhong (钟园)

Department of Physics,ChongQing Three Gorges University,Wanzhou 404100,China

Abstract The quantum phase transition(QPT)and quantum criticality of an anisotropic spin-1/2 XY chain under the interplay of magnetic field and Dzyaloshinskii–Moriya (DM) interaction,which is interpreted as an electric field,are investigated,wherein the anisotropic parameter plays a similar role as the superconducting pairing gap in the interacting Kitaev topological superconductor model that protects the topological order.It is shown that the thermal Drude weight is a good quantity to characterize the gapped (Dth = 0) and gapless (Dth > 0) ground states.The continuous QPT is marked by a quantum critical point (QCP) associated with entropy accumulation,which is manifested by a characteristic Güneisen ratio(GR)with or without selfduality symmetry.It is shown that at a self-dual QCP,the GR keeps a finite value as T → 0,while at a general QCP without self-duality symmetry,it displays a power-law temperature dependent divergence: Γ(T,rc) ～±T-1,which provides a novel thermodynamic means for probing QPT.

Keywords: Grüneisen ratio,self-duality of quantum critical point,XY spin model,Dzyaloshinskii-Moriya interaction

1.Introduction

It is well-known that phase transition plays an essential role in condensed matter physics and material science,which occurs at finite temperature with macroscopic order being destroyed by thermal fluctuations[1,2].The critical point that manifests a continuous phase transition falls into different universality classes in terms of their critical exponents,which are extracted from the singularity of various thermodynamic quantities near the critical point[3].The self-consistency and reliability of the obtained critical exponents are further verified by the scaling hypothesis equations [3,4].However,a different class of phase transition taking place at zero temperature,which is called quantum phase transition (QPT),has attracted much attention recently,which is purely driven by quantum fluctuations rooted in the Heisenberg uncertainty principle[1].Usually,it is caused by changing a non-thermal parameter such as pressure,magnetic field or other coupling constants.When the transition is continuous,it is marked by a quantum critical point (QCP) corresponding to the abrupt change of the ground state[1].Although the QPT takes place at 0 K that cannot be attained experimentally,the quantum criticality becomes rather important and can be detected at ultra-low temperature due to that the thermal fluctuation is not strong enough to excite the ground state.Thus,the quantum fluctuation is still predominant and responsible for the quantum criticality.Of course,such a QCP manifests itself in an unusual sensitivity of thermodynamics at finite temperature upon tuning these non-thermal parameters.

To our best knowledge,the general QPT has been probed by the singular behavior of various order parameters [5–8].Usually,this QCP is not self-dual as a result of the gapped and gapless spectra on two sides of phases such that they cannot be mapped into each other [9].Of course,it was pointed out that the Güneisen ratio (GR) is an important tool to identify and testify a general QCP attributed to the powerlaw temperature dependence of divergence as well as sign change near the QCP [10–12],where the entropy is accumulated.It gives rise to strong signatures of GR near a QCP,which has been observed in heavy fermion metal [10],spin chains [5],metal–insulator transition systems [4] and so on.However,recently,it has been demonstrated by Zhang[9]that self-duality is a necessary condition for the nondivergence of GR at a QCP,in other words,nondivergent GR implies self-duality of the QCP.In particular,it is manifested in the topological QPT with the QCP served as a self-duality,in addition to the sign change of GR near the QCP,wherein it remains finite as T → 0,in distinct contrast to the universal divergence at a general QCP without self-duality.The striking examples are the interacting Kitaev topological superconductor chain [13],the topological insulators [9] and the transverse-field Ising model [14–16],the duality symmetries of which have been performed and analyzed.Noting that the interacting Kitaev topological superconductor chain is governed by the Hamiltonian [13,17],

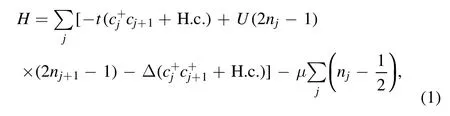
which turns out to be an anisotropic spin-1/2 XYZ chain through the inverse Jordan–Wigner(JW)transformation[18],wherein the quantum coherence witnesses the QPT and quantum criticality [19].Specially,at the symmetric point Δ = t and μ = 0,the system can be exactly solved and transformed into an XY model after the inverse JW transformation combined with a π/2 rotation around x axis,

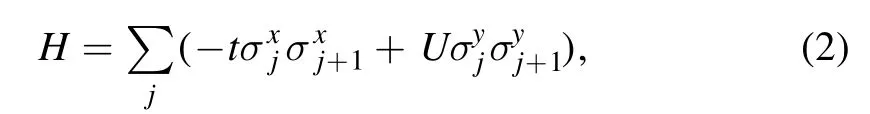
in which the topological QPTs are demonstrated at Uc= ±1 with self-duality QCPs [13].In fact,the above model only considers the symmetric spin–spin interaction responsible for the gapped topological phases with gapless quantum criticality [20].In addition,the antisymmetric Dzyaloshinskii–Moriya (DM) interaction [21,22] as a result of spin–orbit coupling was introduced to explain the weak ferromagnetism in antiferromagnets,which,indeed,induces spin canting and favors the Tomonaga–Luttinger liquid (TLL) state with gapless low-lying excitation [23].Up to now,some spin chain compounds with DM interaction have been found,wherein the spin-flop transition,electron spin resonance and magnetism were investigated [24–27].Furthermore,different exotic extended versions of XY model with DM interaction have been investigated by fermionization technique,which focused on the thermodynamic properties,dynamics,quantum coherence and so on [28–33].However,the nature of quantum fluctuations near the QCP remains enigmatic.Can it demonstrate different self-duality symmetries as well as general QPTs or not? Although several models were carried out to understand the role played by GR in QPTs and detect the QCPs,it is still challenging to measure the GR as an effective detector of QPT to probe different topological and general QPTs in one system.

The goal of this paper is to address these questions.Herein,we focus on the XY spin model with DM interaction in a magnetic field.The thermal Drude weight is a good indicator signaling gapped (Dth= 0) or gapless (Dth> 0)behavior [20,34,35].In the absence of magnetic field,the quantum critical lines by gap closing that separate the gapped topological and gapless TLL phases are identified,in which the topological to topological transition depends on the anisotropy parameter associated with a self-dual QCP,while the QCP signaling the transition from topological to TLL depends on the DM interaction without self-duality,implying a general QPT.As a magnetic field is turned on,when the DM interaction is weaker than the anisotropy parameter,the transverse-field Ising terms predominate,implying that the self-duality at a QCP is Z2symmetry acting on the magnetic field[9,14,15,36,37].Otherwise,the strong DM interaction will break the self-dual symmetry and lead to a general QPT into the TLL phase.Furthermore,to characterize different quantum critical behaviors,the GR is employed.In the forthcoming section,we introduce the model Hamiltonian and briefly describe the fermionization techniques.In section 3,the DM interaction and magnetic field induced phase diagrams associated with quantum criticality are explored; the duality symmetry at a QCP is performed and analyzed by the GR.Finally,a conclusion is drawn in section 4.

2.Model Hamiltonian and method

The anisotropic spin-1/2 XY chain with DM interaction in an external magnetic field is described by the following Hamiltonian [28–33],

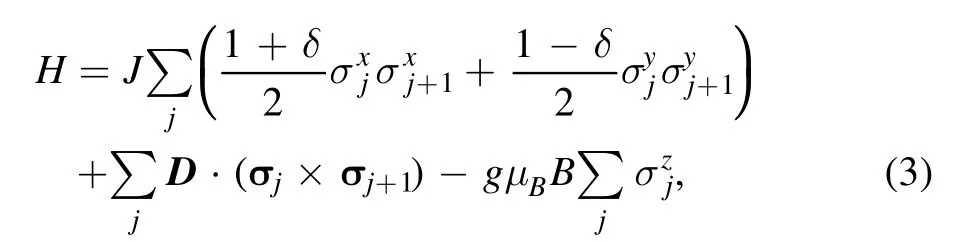
where J > 0 manifests the antiferromagnetic exchange coupling anddenote the Pauli matrix.Herein,the DM vectorD=Dzand external magnetic fieldBare presumed along the z direction.According to the microscopic mechanism of electric polarization in nonlinear spiral magnets,the magnitude of DM interaction can be interpreted as an electric field along the y direction coupling to the polarization operator:P∝eij× (σj× σj+1) (i.e.,whereeijis the unit vector along x direction pointing from site j to site j+1 [19,38].Hence,the DM term in Hamiltonian (3) represents an auxiliary energy induced by the electric field:-D·P.Besides,-1 ≤ δ ≤ 1 is the anisotropic parameter.The limitsδ= ±1 andδ= 0 represent the Ising model and the isotropic XX chain,respectively.Apparently,the Hamiltonian (3) describes an anisotropic XY chain in the presence of magnetic and electric fields,wherein the anisotropy,DM interaction and Zeeman energy compete with each other,resulting in QPTs.

By performing the Jordan–Wigner (JW) transformation[18],

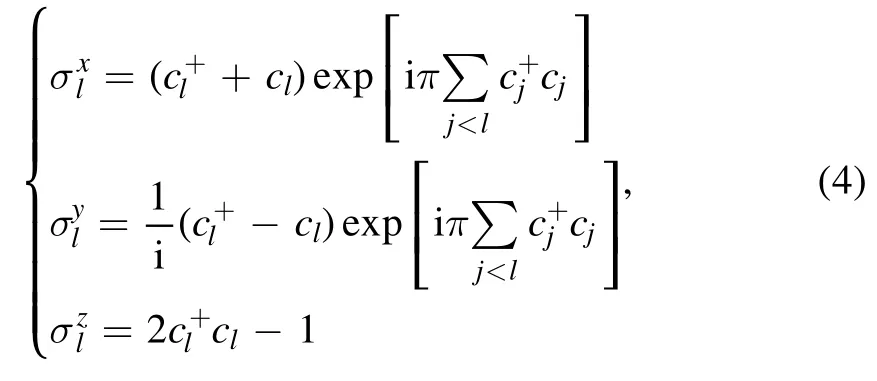
one can obtain

withh=gμ BBthe reduced magnetic field (Zeeman energy).

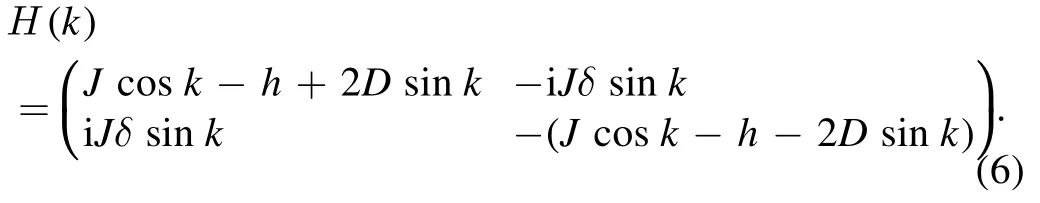
Diagonalizing the Hamiltonian,one can obtain the energy spectrum,i.e.,eigenvalues,

Thus,the free-energy density is expressed as [30–40],

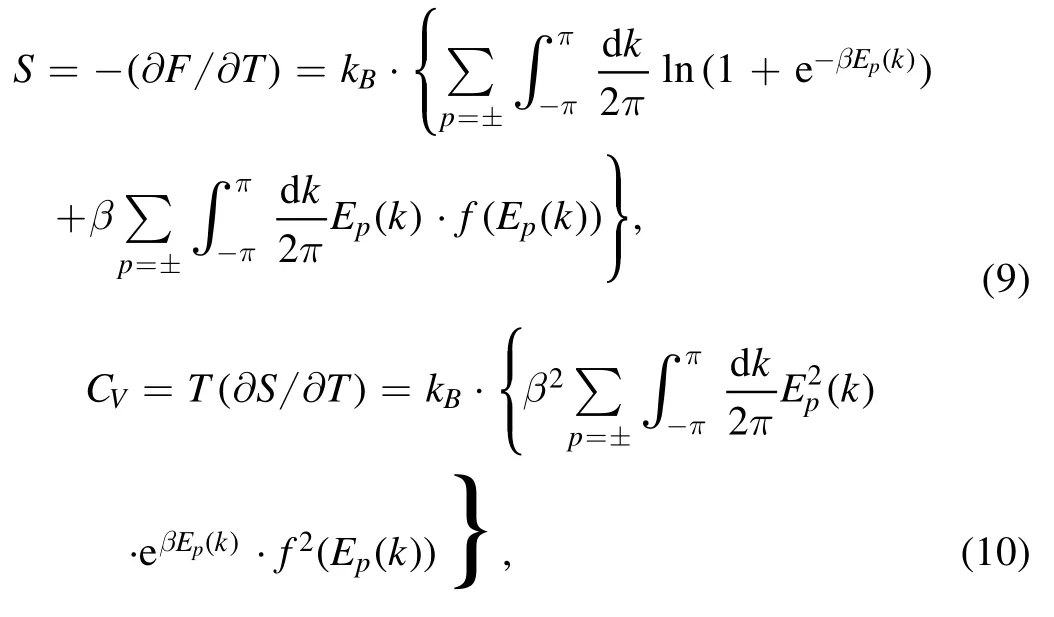
with the Fermi–Dirac distribution function

The Grüneisen ratio is defined as [10–12]

3.Results and discussion

In what follows,kB= ħ = 1 and J = 1 is set as an energy unit,hereafter all other parameters are scaled by it.In the absence of DM interaction,the Hamiltonian (5) is equivalent to a non-interacting Kitaev topological superconductor model in the spinless fermion map,wherein the anisotropy δ amounts to the p-wave superconducting paring gap Δ that protects the topological order[13,17],and h plays the role of chemical potential μ.However,as the DM interaction emerges,it induces spiral spin order that favors the gapless TLL state,giving rise to the competition between topological and TLL phases that are manifested by δ and D.The former is gapped,while the later is gapless.It is worth noting that the gapped and gapless low-lying excitations in low-dimensional spin systems can be evidenced by the thermal Drude weight(i.e.,zero-frequency weight of the thermal conductivity within the Kubo linear response theory):Dth=withjththe energy current[34,35].It is well-known that Dth= 0 and Dth> 0 at T = 0 denote the thermal insulator and ideal thermal conductor,implying the gapped and gapless behaviors,respectively.At first sight,in the absence of the magnetic field,the D-δ ground state phase diagram containing topological and TLL phases,is unveiled by the contour of thermal Drude weight,as shown in figure 1(a).It is shown that the phase diagram is symmetrical with δ = 0,at which,in particular,for D = 0,the ground state is gapless,demonstrated by the sharp peak of thermal Drude weight in figure 1(b).For nonzero DM interaction,it presents two critical points atδc= ±2D,beyond which Dth= 0 signals the gapped topological phase,while between which Dth> 0 denotes the gapless TLL state.Similarly,the entropy shows symmetry with δ = 0 and a sharp peak at the δc(see figure 1(c)),indicating QPT,because it is not determined which state to be resided in.Furthermore,in figure 1(d),the symmetry is demonstrated by the D dependence of entropy for±δ,which overlaps and displays a sharp peak at Dc= 1/2δ,signaling the QCP.Thus,one can obtain two critical linesD=that separate the topological and TLL phases.

Figure 1.For h=0 and T = 0.005,(a)D-δ phase diagram;(b)thermal Drude weight and(c)entropy as a function of δ for D = 0 and 0.25;(d) D dependence of entropy for δ=-0.5 and 0.5.

It is well shown that the QPTs are continuous one.How are the critical properties effectively described? The GR is a good quantity.In the absence of DM interaction,it is equivalent to the interacting Kitaev topological superconductor model after the Jordan–Wigner transformation and spin rotation,the QPT of which occurs at δ=0,signaling a gapped one to another gapped one.In Majarana fermion representation,one complex fermion operator can be split into two Majarana fermion operatorsandwith the Majarana fermion operator being realand satisfying the anticommutation relation= 2δ jl δab(a,b = 1,2) [13].Thus,the Hamiltonian(4) becomes

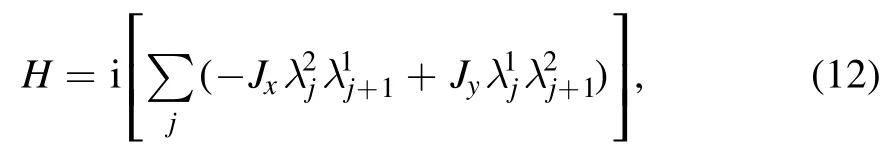
whereJx=J(1 +δ)/ 2andJy=J(1 -δ)/ 2.Obviously,duality symmetry exists between δ < 0 and δ > 0,which imposes the QCP at δ = 0.By interchanging the Majarana fermion operator as follows,

The Hamiltonian will keep the same form with spin coupling changes as

Note that δ = 0 is the self-dual QCP separating the topological phases.Nevertheless,the duality is not a unitary transformation[37].Near the QCP,the GR as a function of δ under different temperatures is plotted in figure 2(a).At low temperature,the sign change of Γ(T,δ)close to QCP coincides with the general scaling form Γ(T,δ)～1/(δ-δc),as is shown in the inset of figure 2(a),wherein the inverse of GR against δ behaves linearly.Strikingly,the curves intersects precisely at the QCP and Γ(T,δc) = 0 independent of temperature (see figure 2(b)),which deviates from the divergence of universal scaling prediction Γ(T,δc) = -GTT-1in the QC regime.Recalling figure 1(a),for a fixed D value along the horizontal direction,it demonstrates tuning δ through different regions of the phase diagram.Near the QCPs,the sign of Γ(T,δ)changes but does not intersect,as shown in figure 2(c),because of a gapped topological phase transition into a gapless TLL one,or vice versa.In this case,the self-dual symmetry is broken.Hence,the Güneisen ratio manifests the universal scaling divergence Γ(T,δc) ～T-1(see figure 2(d)).At a fixed δ value along the longitude direction,the self-dual symmetry of QCP is also broken,as a result of the gapped and gapless in the topological and TLL phases,respectively,which can not be mapped into each other by fermion operation transformation.The GR near the QCP is shown in figure 2(e),wherein Γ(T,D)changes sign as the scaling form Γ(T,D)～1/(D-Dc) (see the inset).Similarly,at the QCP,Γ(T,Dc)diverges as T → 0 with the power-law fitting yielding Γ(T,Dc) ～-T-1,which is in sharp contrast to the self-dual QCP.

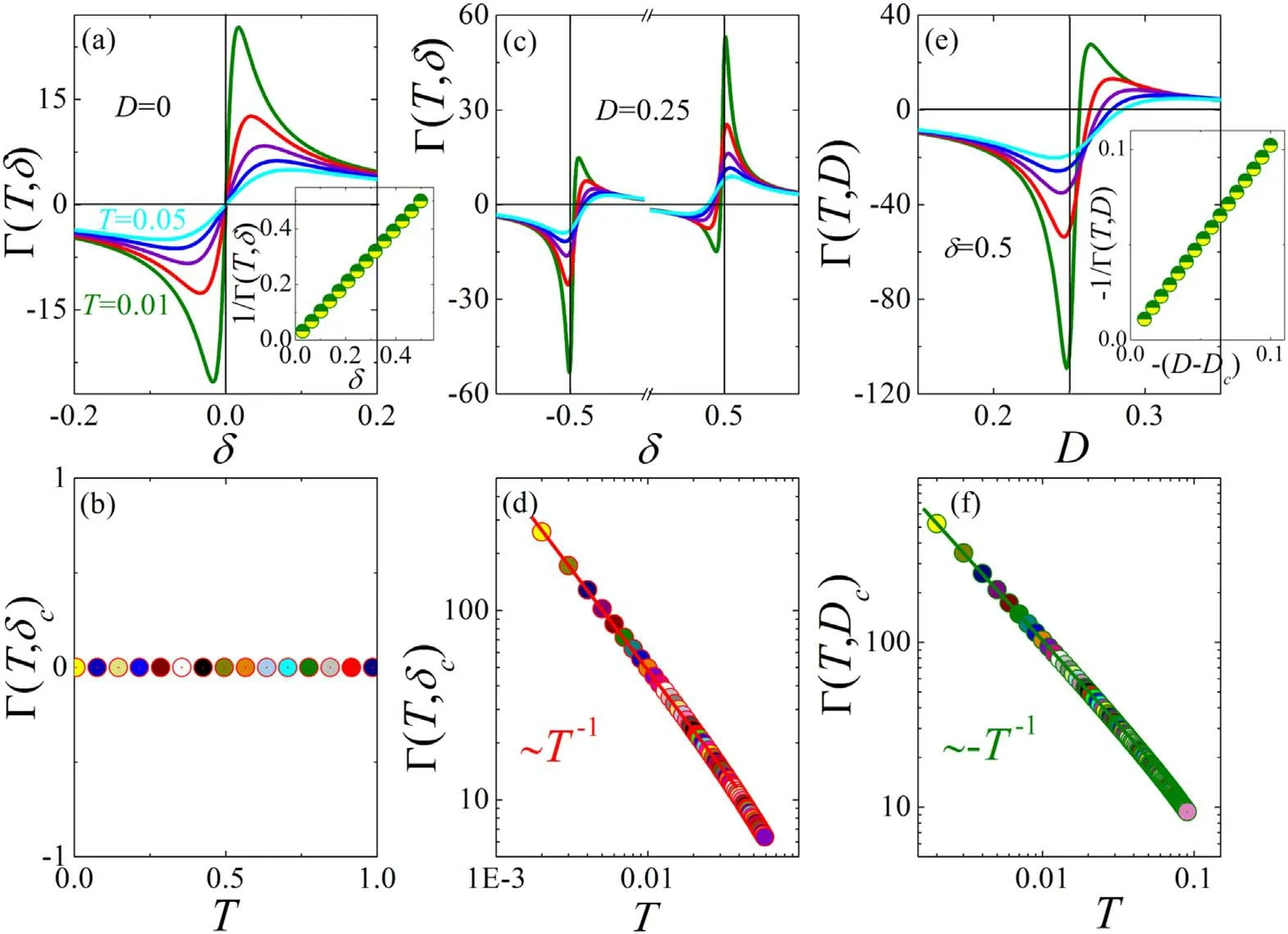
Figure 2.From T = 0.01 to 0.05,Güneisen ratio as a function of δ for(a)D = 0 and(c)D = 0.25;the inset in(a)is the inverse of Güneisen ratio as a function of δ at the lowest temperature.(e)Güneisen ratio as a function of D for δ=0.5,the inverse of Güneisen ratio as a function of(D-Dc)is plotted in the inset at the lowest temperature.The temperature dependence of critical Güneisen ratio for(b)D = 0,(d)D = 0.25 and (f) δ=0.5.

As a magnetic field is turned on,it brings to plentiful QPTs.In the absence of DM interaction,first,it is reduced to spin-1/2 XX chain with δ = 0,which can be diagonalized exactly,

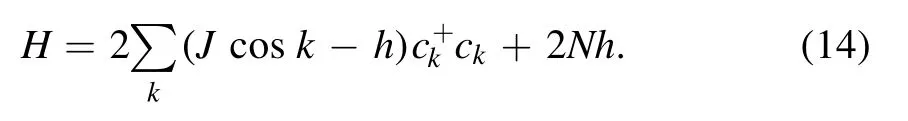
One can find that the system is partially filled by JW fermions for h < 1.0,while it is completely pushed down into Fermi sea beyond h = 1.0.The QPT takes place at hc= 1.0,which is similar to the metal–insulator transition in 1D correlated electron system[9].In this case,the self-duality is broken by the zeeman splitting.Near the QCP,in figure 3(a),the GR Γ(T,h) changes sign and takes the scaling form Γ(T,h)～1/(h-hc) at the lowest temperature (see the inset).At the QCP,Γ(T,hc) shows a power-law divergence:Γ(T,hc) ～T-1upon cooling down to zero temperature,as plotted in figure 3(b).

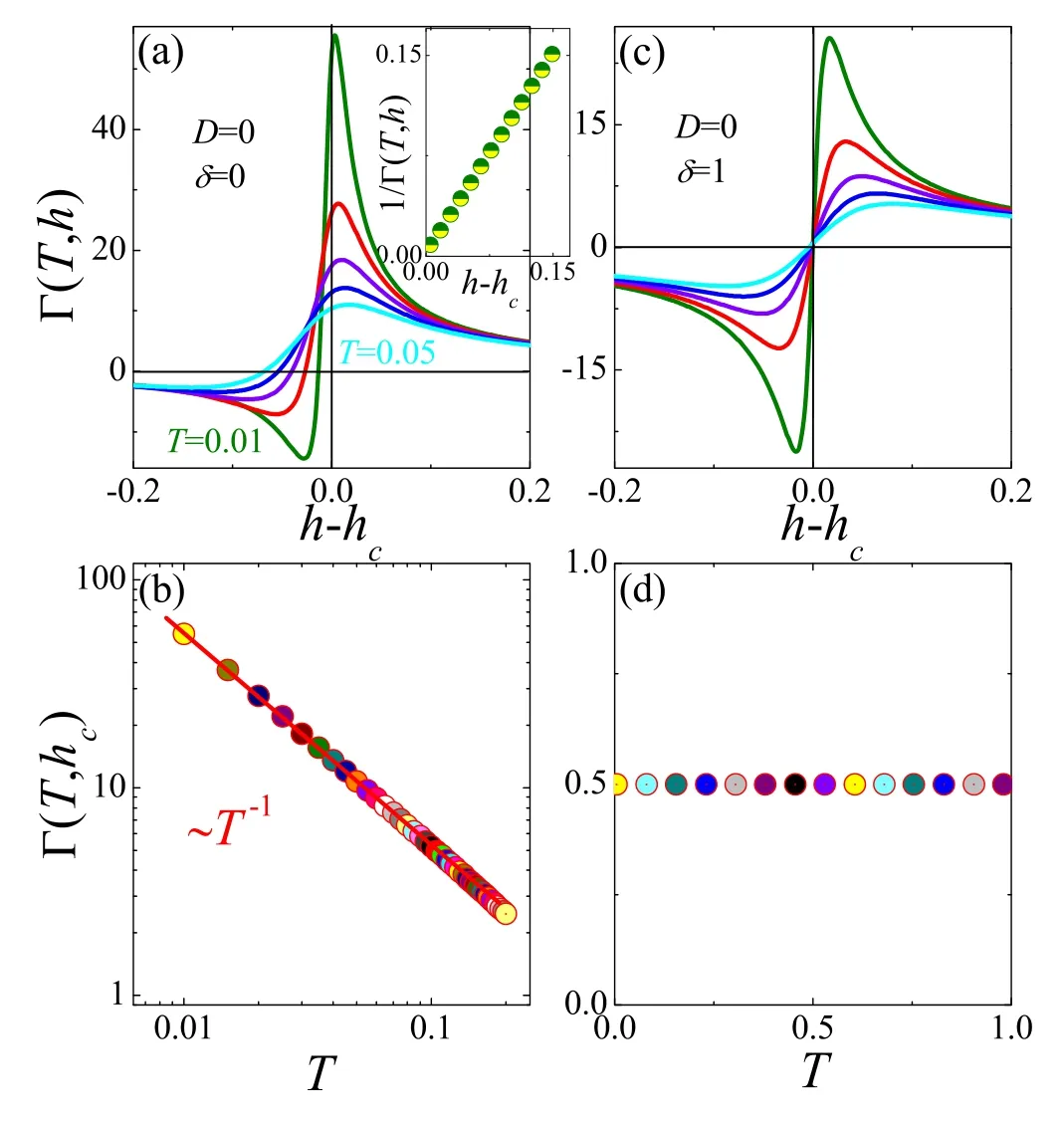
Figure 3.For D = 0,the field dependence of Güneisen ratio under different temperatures in (a) δ=0 and (c) δ=1; the inverse of Güneisen ratio as a function of (h-hc)is plotted in the inset of (a)at the lowest temperature; the temperature dependence of critical Güneisen ratio in (b) δ=0 and (d) δ=1.0.

For δ = 1.0,the system becomes a transverse-field antiferromagnetic Ising model,

In the fermion presentation,the local unitary transformationinterchanges J and –J [41].Thus,the Hamiltonian (14) is simplified as

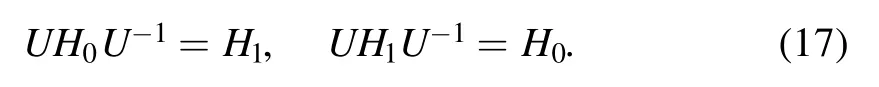
It keeps Abelian Z2symmetry under self-duality transformation,UH(hc)U-1=H(hc).In figure 3(c),it is clearly shown that near hc,the Güneisen ratio Γ(T,h) changes sign and intersects precisely at the QCP.At finite temperature,according to the maxwell relation and self-duality transformation,the GR at hcis calculated as

In figure 3(d),one can find that the GR Γ(T,hc) = 1/2 is independent of the temperature.

However,the DM interaction has a more important impact on the QPTs and quantum criticality of the system.In figure 4(a),for a fixed δ = 0.5,the D-h phase diagram is cut apart into three regimes: topological,TLL and ferromagnetic(FM) phases,which are labeled by three critical lines:h = 1.0,D = 1/2δ and h = (4D2- δ2+ 1)1/2,respectively.One can find that in the topological and FM phases,Dth= 0 demonstrates the gapped behavior,while in the TLL regime,Dthbecomes finite,suggesting the gapless low-lying excitation.Of course,the phase boundaries are manifested by the QCP of the entropy,the field or DM interaction dependence of which presents a sharp peak,as shown in the figure 4(b)and the inset.In particular,for D < 1/2δ and h < 1.0,the ground state lies in the topological state,because the Ising order wins over the DM interaction and Zeeman splitting,which is responsible for the topologically nontrivial phase.As a matter of fact,Jx> Jy,the x-x correlation is dominant,and then,beyond h=1.0,the field may induce Ising-type QPT.The QCP is captured by the sign change of Γ(T,h) as a function of h at low temperature,as shown in figure 5(a),which still takes the scaling form Γ(T,h)～1/(h-hc).Thus,for D < 1/2δ,the transverse-field Ising terms are predominant,while the y-y correlation and DM interactions can be regarded as perturbed terms,which approximately keeps the self-duality Z2symmetry of the QCP [9].As T → 0,at hc= 1.0,the GR Γ(T,hc) tends to a finite value and can be expanded as Taylor’s series,

Figure 4.For δ = 0.5,(a)D-h phase diagram;the field dependence of(b)entropy and(c)correlation function with different DM interactions;(d)the correlation function as a function of D under different fields;the inset in(b)is the D dependence of entropy,while the inset in(c)is the first derivative of correlation function.

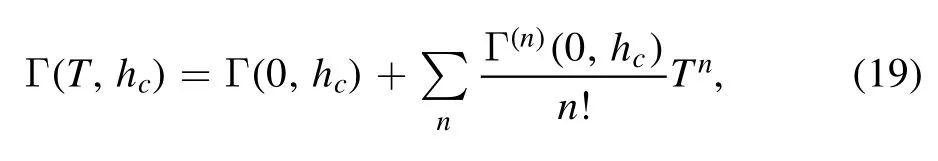
which is demonstrated in figure 5(b) and similar to the topological QPT occurred in quantum anomalous Hall insulator.Furthermore,from figure 4(c),one can see that the x-x correlationas a function of h overlap with each other and shows continuous variation with a hidden QPT for D < 0.5δ,which is manifested by the sharp peak of the field derivative at h = 1.0 (see the inset),indicating the typical transverse-field Ising properties.However,for D > 0.5δ,the DM interaction is predominant,resulting in the spin canting responsible for the gapless TLL phase.Beyond hc= (4D2- δ2+ 1)1/2,it will go into the FM phase,which is clearly demonstrated by the singularity of the field dependence of Cxx.The quantum criticality is also manifested by the sign change of the field dependence of GR Γ(T,h)(see figure 5(c)).Nonetheless,the self-duality symmetry is broken by the DM interaction associated with gapless and gapped phases near hcthat cannot be mapped into each other,giving rise to the power-law temperature divergence Γ(T,hc) ～T-1(see figure 5(d)).In another way,below h=1.0,the dominant x-x Ising coupling is manifested by the D dependence of Cxxthat stays at a constant(see figure 4(d)),which is responsible for the topological order.Strikingly,the absolute constant decreases slightly because of the gradual enhancement of Zeeman energy.The GR Γ(T,D)near Dc= 1/2δ with its sign changed is shown in figure 5(e),which takes the scaling form Γ(T,D)～1/(D-Dc).At the QCP,in figure 5(f),Γ(T,Dc)diverges as T → 0 with a power-law temperature dependence Γ(T,Dc) ～-T-1,because of the broken self-dual QCP.

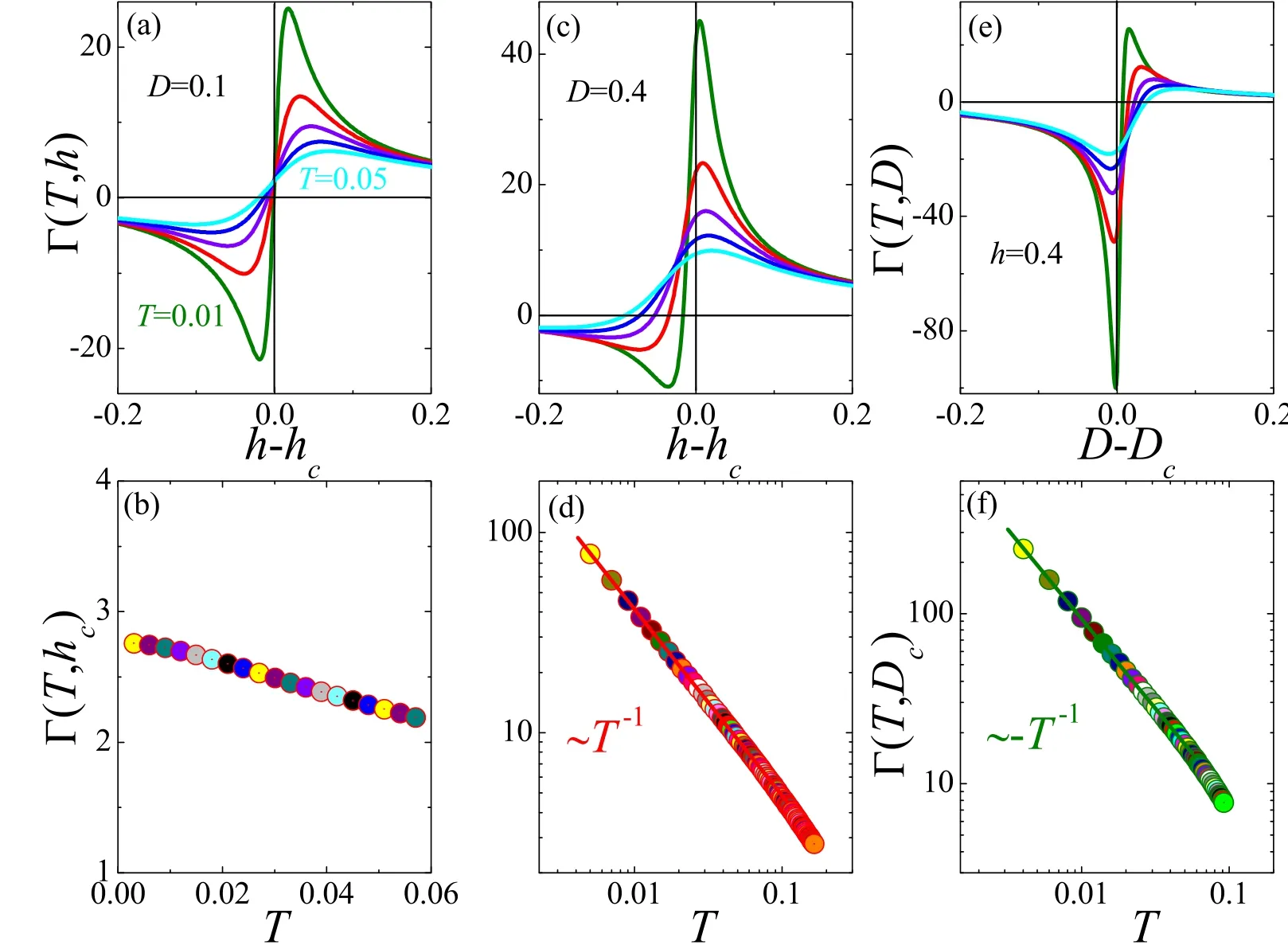
Figure 5.At low temperatures,for δ=0.5,the field dependence of Güneisen ratio in (a) D = 0.1 and (c) D = 0.4; (e) Güneisen ratio as a function of D with h=0.4; the temperature dependence of critical Güneisen ratio in (b) D = 0.1,(d) D = 0.4 and (f) h=0.4.

4.Conclusion

In conclusion,the QPT and quantum criticality of spin-1/2 XY chain with DM interaction is investigated,which is exactly solvable within the Jordan–Wigner transformation.It is shown that the thermal Drude weight is a good quantity to characterize the gapped (Dth= 0) and gapless (Dth> 0)ground states.The continuous QPT is marked by a QCP,demonstrated by a characteristic GR with or without selfduality symmetry.In the absence of DM interaction and magnetic field,it is reduced into an anisotropic XY chain,which can be mapped into an interacting Kitaev topological superconductor model within spinless fermion presentation,wherein the anisotropic parameter δ plays the same role as that the superconducting pairing gap Δ protects the topological order.Evidently,δc= 0 is a self-duality QCP manifesting gapped topological QPT across the gapless QCP,characterized by the GR Γ(T,δc) = 0 independent of temperature.As the DM interaction emerges,it induces a QPT into a gapless TLL phase with the self-duality symmetry broken.In a magnetic field,for D = 0 and δ = 1.0,the system is reduced into a transverse-field Ising model with self-duality Z2symmetry at hc= 1.0,which is demonstrated by the GR Γ(T,hc) = 1/2 irrelevant of temperature.

In addition,in a general case,the transverse-field Ising terms are predominant for D < 1/2δ,which still keeps the self-duality Z2symmetry approximately at hc= 1.0,demonstrated by a saturated value of Γ(T,hc) upon cooling down to zero temperature.However,for D > 1/2δ,the selfduality symmetry of QCP is broken such that the GR displays a power-law divergence: Γ(T,rc) ～±T-1.Therefore,the GR that remains finite as T → 0 should be identified and served as a universal thermodynamic signature of self-duality QCP.