Monte Carlo study of the magnetic properties and magnetocaloric effect of an AFM/FM BiFeO3/Co bilayer
2021-10-13ChunluChangWeiWangHeMaHanHuangJinchengLiuandRuizeGeng
Chun-lu Chang,Wei Wang,∗,He Ma,∗,Han Huang,Jin-cheng Liu and Rui-ze Geng
1 School of Science,Shenyang University of Technology,Shenyang 110870,China
2 School of Electrical Engineering,Shenyang University of Technology,Shenyang 110870,China
Abstract The magnetic properties and magnetocaloric effect of an antiferromagnetic/ferromagnetic(AFM/FM)BiFeO3/Co bilayer with mixed-spin(5/2,3/2)have been studied based on Monte Carlo simulation.The magnetization,susceptibility,and critical temperature are investigated under various exchange couplings and an external magnetic field.In particular,the influence of exchange couplings and an external magnetic field on the magnetic entropy change,adiabatic temperature change,and the relative cooling power(RCP)are studied.The simulation results indicated that the decrease of the exchange coupling and the increase of external magnetic fields can cause an increase of magnetic entropy change,adiabatic temperature change,and RCP.In addition,the hysteresis loops of the system are presented for different exchange couplings and temperatures.
Keywords: BiFeO3/Co bilayer,magnetization,critical temperature,entropy change,hysteresis loops,Monte Carlo simulation
1.Introduction
BiFeO3belongs to the family of multiferroic materials and also encompasses ceramic materials.It can play a significant role in the application of magnetoelectric read heads [1],magnetoelectric transformers [2],memory devices [3],and tunable microwave devices [4].In practical applications,BiFeO3-based components,such as the BiFeO3/Co bilayer,which can be synthesized by rapid hot pressing[5],solid-state reaction methods[6],the Pechini method[7],and so on,have attracted much attention.In addition,much effort has been devoted to the study of the magnetic,as well as electrical properties of the BiFeO3/Co bilayer based on diverse methods from theoretical and experimental aspects[8–10].
In recent years,research on the magnetocaloric effect(MCE),which was first proposed in 1881 by Warburg[11],is attractive because of its potential application in sustainable energy-related emerging technologies,for instance,magnetic refrigeration[12–15].As far as we know,MCE is an intrinsic and exciting nature of the magnetic system,which can be defined by the fact that the temperature of a ferromagnet varies with the strength of the magnetic field in an adiabatic process [16,17].From a physical point of view,MCE is directly related to the coupling between magnetic atoms in the magnetic sub-lattice and the applied magnetic field [18].It is worth mentioning that isothermal entropy change (-ΔS),adiabatic temperature change (ΔTad),and relative cooling power (RCP) are representative characteristics that can better describe MCE,and these parameters are necessary to obtain a high magnetic refrigeration efficiency [19].There are many investigations on the experimental and theoretical study of MCE.Experimentally,there are many reports of MCE on diverse nanoparticles or compounds.To name a few,the Ln0.67Sr0.33MnO3(Ln =La,Pr,and Nd) nanoparticles were fabricated by the sol-gel method,and much work was devoted to studying their structural and magnetic properties [20].Another conclusion is that all the samples showed considerable MCE in a wide temperature range.Some research results indicated that the physical properties of thin films are different from their bulk counterparts [21,22].A report suggested that MCE was successively reached at a low magnetic field [23],and the study also paid attention to the MCE of Ni-Mn-Ga thin films.Further,some other studies focused on the LaFe13-xSixcompounds [24],Heulser alloys Ni-Mn-X with (X =Ga,Sn,…) [25],[Gd/Tb] multilayers[26],and so on.The experimental research of BiFeO3-based ceramics shows that the external magnetic and electric field have a significant influence on the magnetic properties of the system [27,28].In addition,the atom doping concentration can modify the MCE of the BiFeO3-based system [29].
On the other hand,more efforts have been devoted to the theoretical investigations of MCE for nanomaterials,such as nanoparticles,nano-compounds,and thin film by various methods.A study was implemented by Hu et al to study the MCE in anisotropic zinc ferrite nanoparticles based on Monte Carlo (MC) simulation [30].The magnetic entropy change and adiabatic temperature change were predicted in detail,and the emphasis was on the effect of anisotropy on these properties.In order to foster favorable materials for magnetic refrigeration devices,a study was carried out on the magnetic properties and MCE of the MnFe4Si3system based on the MC method[31].The structure was composed of a hexagonal lattice with Fe (S=3/2) and Mn (S=3/2).The magnetic entropy change,adiabatic temperature change,RCP,as well as magnetization,were obtained for different parameters and discussed in detail.In addition,the second-order phase transition was predicted at the Curie temperature.The results in this study provided good proof that MnFe4Si3can be a suitable material for magnetic refrigeration.At present,many researchers are dedicated to the investigation of MCE for thin films by various methods.Giant magnetic entropy change is mainly rooted in the magnetic state change,which was concluded from a study of magnetic properties and MCE of multifunctional α-FeRh thin films [32].MC simulation,as one of the most conventional and successful methods,has also been extended to study the MCE of thin films.An investigation of MCE for La1-xCaxMnO3thin films based on this method revealed that the external magnetic field has an important impact on MCE for such thin films [33].The surface effect on the magnetocaloric properties of perovskite ferromagnetic thin films was studied by Elyacoubi et al based on MC simulation[34].Some results were discussed in detail,such as the maximal entropy change and that RCP increases when enlarging the external magnetic field,while RCP decreases when the value of the surface exchange coupling increases.In the field of theoretical calculation of magnetic nanomaterials,the mixed-spin Ising model is a well-known model which can help in understanding the magnetic nature of various magnetic nano-systems and could be taken into account to investigate the MCE.Albayrak studied the entropy and isothermal entropy change of the mixed-spin(1,1/2)Ising model [35].The influence of the crystal field and external magnetic field on the variation of the peak value of isothermal entropy change was discussed emphatically.Apart from the research mentioned above,there are many other investigations on the MCE of thin films,for instance AlCMn3[36],NdMnO3[37],Ho3Pd2[38],Sr2CrMoO6[39],Sr2CrIrO6[40],and SmFe1-xMnxO3[41].All these studies reveal that exchange coupling and an applied external field play a significant role in the variation of the MCE,and this is exactly what our present research focuses on.
In our previous works,the MC simulation and the Ising mixed-spin model were significantly applied to investigate the magnetic,electric,as well as thermal dynamic,properties of various nanosystems[42–48].We have ever devoted ourselves to the study of the dielectric properties of the BiFeO3/FM bilayer system [49].It should be mentioned that there have been many experimental[50,51]and theoretical[52,53]works which have studied the MCE behavior of multiferroic materials,and a study has released that BiFeO3has great potential applications because of its higher Curie temperature (TC=1100 K) and Nell temperature (TN= 650 K) [54,55].However,few theoretical works have been conducted on the MCE in an AFM/FM BiFeO3/FM bilayer system.This further stimulated our interest to conduct such a study to discuss,in depth,the effect of exchange coupling,the external magnetic field on MCE,and the magnetic properties of the BiFeO3/FM bilayer system.The rest of this paper is arranged as follows: in the next section,the model and the method applied to this study are presented.In the third section,we show the detailed results of the simulation and provide some discussion.The last section includes a brief summary.
2.Model and method
An AFM/FM BiFeO3/Co bilayer with mixed-spin(5/2,3/2)consisting of 2N2×L spins on a three-dimensional honeycomb lattice,as plotted in figure 1,is constructed.N and L are defined as the number of spins in each layer and the thickness of the bilayer system,respectively.For such a bilayer system,we adopt L=2.
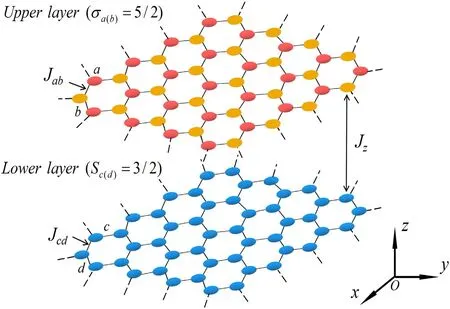
Figure 1.The schematic of an AFM/FM mixed-spin (5/2,3/2) Ising model with a BiFeO3/FM bilayer structure.
The Hamiltonian of the system is considered as follows:
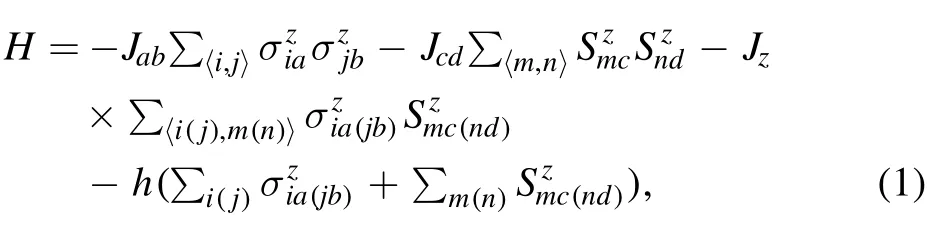
where the first item Jab(<0) represents the intralayer exchange coupling between sublattices a and b in the upper layer,and Jcd(>0)refers to the intralayer exchange coupling between sublattices c and d in the lower layer.Jzdenotes the interlayer exchange coupling which is positive between sublattices a and c,but negative between sublattices b and d.In the whole simulation process,Jabis considered to be the unit of energy and temperature,thus |Jab| takes the value of 1.〈i,j〉,〈m,n〉,and〈i,m〉stand for the summation over all the first nearest neighbor sites at sublattices a,b,sublattices c,d,and between sublattices a(b)and c(d),respectively.are the z-component spins of spin-5/2 with the values ±5/2,±3/2,±1/2 andare the z-component spins of spin-3/2 with the values±3/2,±1/2.The last item h is the applied external magnetic field.
The method used for this simulation to calculate the BiFeO3/Co bilayer is MC simulation based upon the standard Metropolis algorithm [56].For the present bilayer,the periodic boundary condition is applied in the xy plane,and the free boundary condition is considered in the z-direction.In order to determine the finite-size effect caused by the number of each layer 2×N2for such a bilayer system,we present in figure 2 the temperature dependence of susceptibility χ when 2×N2is changed from 2×52to 2×502with fixed|Jz|/|Jab|=0.8,Jcd/|Jab|=1.2,T/|Jab|=0.05.From the figure,we can see every χ curve has a peak that corresponds to a temperature defined as critical temperature (TC).It is an important parameter for better understanding magnetic phase transition from order to disorder for magnetic nanostructures[28,34,35].It is found that the χ curves intersect each other at the same TCwhen 2×N2is larger than 2×202,whereas the TCappears earlier for 2×N2smaller than 2×202,suggesting that the system can exhibit an obvious finite-size effect for small size.Consequently,in order to save computation time,we choose 2×N2=2×202for the following simulation.In order to balance the system,the first 2×105MC steps (MCS) among the total was abandoned in our simulation and we used the rest 3×105MCS to calculate the average values of the thermodynamic quantities as follows:
The magnetization of sublattices a,b,c,and d are calculated as:

Figure 2.The temperature dependence of χ for different system sizes 2×N2 with |Jz|/|Jab|=0.8,Jcd/|Jab|=1.2.
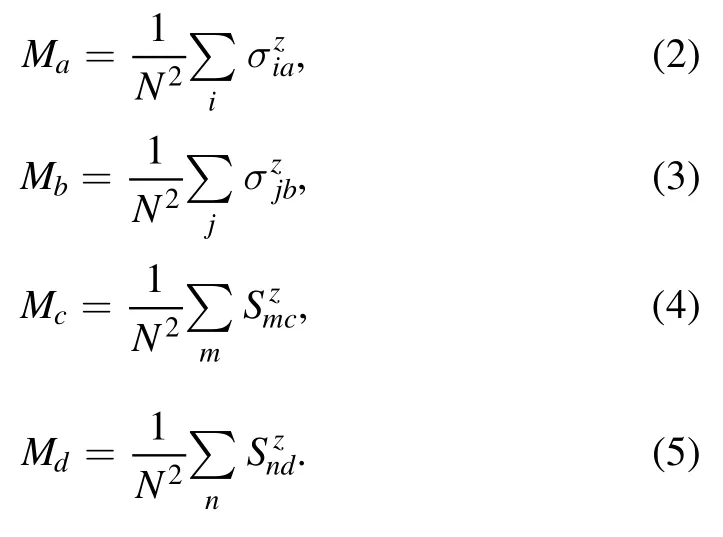
Thus,the total magnetization of the system is shown as:

The total susceptibility of the bilayer system is:
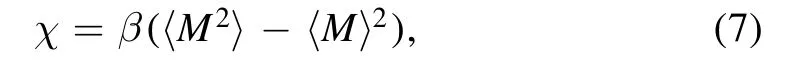
The characterization of the MCE can be described by the following formulas:
The magnetic entropy per site is obtained by:
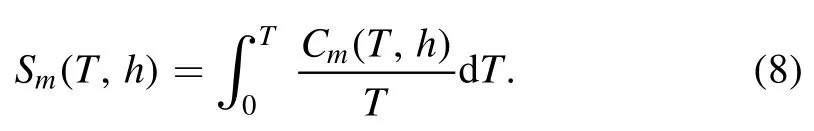
The magnetic entropy change is presented by:
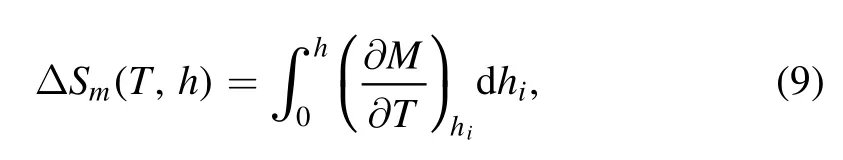
The adiabatic temperature change is deduced by:
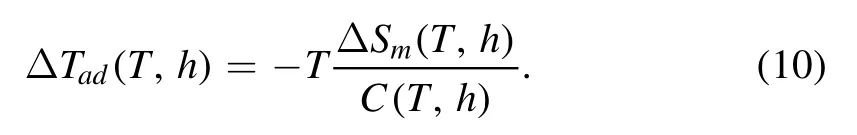
The C appearing in the above equation is the representation of the total magnetic specific heat.The lattice term,electronic term,and magnetic term are taken into account.On the strength of the Debye model[57],the approximated value of it can be described as:
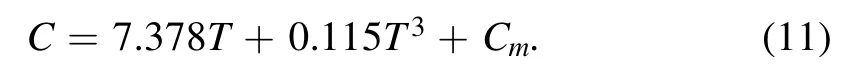
Finally,the RCP of the system is given by:
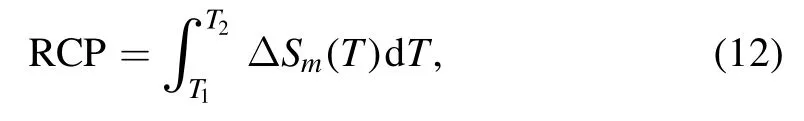
T1and T2are the cold and hot temperatures corresponding to both ends of the 1/2-maximum value ofΔ,respectively.
3.Result and discussion
In this section,some significant results of the effects of multifarious physical parameters,for instance,exchange couplings (Jcd,|Jz|) and external magnetic field h on the magnetic properties,the MCE as well as the hysteresis loops of a mixed-spin (5/2,3/2) Ising bilayer,are presented in detail and discussed.
3.1.Magnetization and susceptibility
Figure 3 shows the magnetization(M),susceptibility(χ),and the critical temperature (TC) of the bilayer system under the influence of the exchange interaction Jcdwith other fixed parameters |Jz|/|Jab|=0.8,h/|Jab|=0.5.Figure 3(a) shows the variation of magnetization with Jcd.Just one saturation is observed,so a conclusion can be drawn that M is not sensitive to the variation of interlayer exchange interaction Jcd.The M curve holds a constant when Jcd/|Jab|=2.0 for T is lower(0 ~1),while with the decreasing of the value of Jcd/|Jab|,this phenomenon gradually becomes inconspicuous.In the perspective of theory,the magnetization is presented under the interaction of exchange coupling,temperature,and external magnetic field.A larger exchange coupling value is more advantageous in competition with temperature,which causes the spins in the sublattice to align in its direction,thus showing a stable magnetization externally.However,when the exchange coupling decreases or the temperature increases,the spins have more chance to flit,so the magnetization changes for the response.It gradually decreases with the increase in temperature,and at the same temperature,it decreases with the decrease of Jcd/|Jab|.A similar phenomenon can also be seen in [38,58].The total susceptibility of the system varying with Jcdis displayed in figure 3(b).The six χ curves have the same shape.As the temperature rises,χ first increases and then gradually decreases after reaching a peak.The increase of Jcd/|Jab| can cause the position of the peak to shift to a higher temperature region.Physically,with the increase of Jcd/|Jab|,more thermal energy is needed to overcome the forces from exchange coupling to break the magnetic order,thus TCincreases correspondingly.For a deeper understanding of the variation of TCwith Jcd,the TCcurve is plotted in the (TC-Jcd/|Jab|)plane.In figure 3(c),a smooth curve can be seen.With the increase of Jcd/|Jab|,the curve gradually extends upward.In addition,the TCcurve splits the entire phase plane into two parts,with the ferromagnetic phase below TCand the paramagnetic phase above TC.A similar phenomenon can be seen in [47,48].
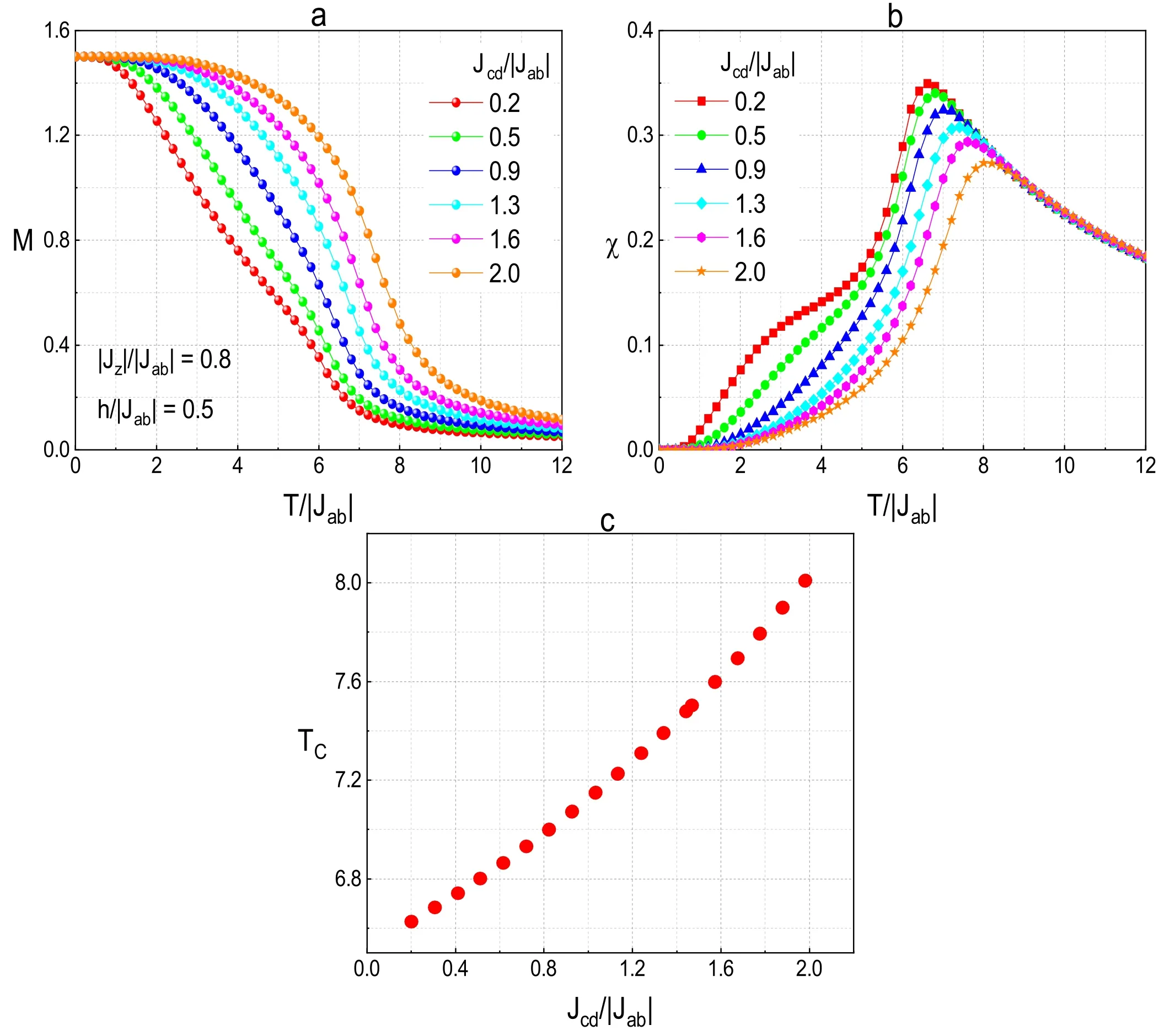
Figure 3.The influence of Jcd on a) M,b) χ,and c) TC with fixed |Jz|/|Jab|=0.8,h/|Jab|=0.5.
Similarly,as shown in figure 4,the influence of intralayer exchange coupling |Jz|/|Jab| on M,χ,TCwhen Jcd/|Jab|=1.2,h/|Jab|=0.5 is studied.The M curve plotted in figure 4(a) is slightly different from that in figure 3(a).There is just one saturation as well,but as the temperature rises,the six M curves finally coincide with each other,which is different from the phenomenon in figure 3(a).Figure 4(b)shows the change of TCwith |Jz|.Obviously,the peak of the curves shifts to the right as |Jz| increases.The curve is shown in figure 4(c),depicted in the (TC-|Jz|/|Jab|) plane.It is clear that as |Jz|/|Jab| increases,the TCgoes up in response.The phase plane is also divided into two parts by TC—the lower and upper parts correspond to the magnetic phase and paramagnetic phase,respectively.Taking interlayer exchange coupling Jcdand intralayer exchange coupling |Jz| into consideration,we can conclude that both have a similar impact on χ and TC.Similarly,these results are in good accordance with that in [46,48,58,59].
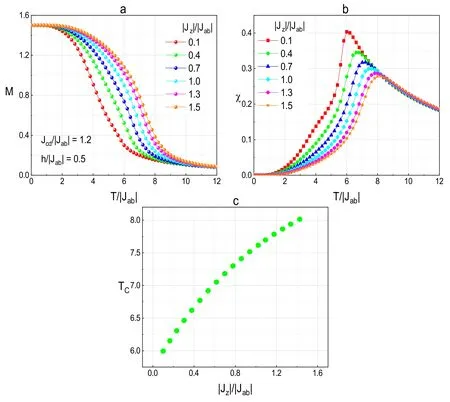
Figure 4.The influence of |Jz| on a) M,b) χ,and c) TC with fixed Jcd/|Jab|=1.2,h/|Jab|=0.5.
3.2.Magnetocaloric effect
Figure 5 shows the magnetic entropy change (-ΔS) and adiabatic temperature change(ΔTad)of the bilayer system for different values of Jcd/|Jab| for fixed values of Δh/|Jab|=0.5,|Jz|/|Jab|=0.8.From figure 5(a),a phenomenon can be seen whereby -ΔS initially increases with the increase of T/|Jab|,and then decreases with the continuous increase of T/|Jab| after reaching the maximum value.We have to mention that the temperature corresponding to the maximum is near the critical temperature.This is consistent with that shown in[14,37,40],which present that the maximum of the-ΔS appears in the vicinity of the critical temperature.Thus,the prominent increase in the variation of -ΔS results from the heat that the system releases during the phase transition.Turning our attention to figure 5(b),similar curves to those shown in figure 4(a) are seen again.The biggest difference between them is the order of magnitude.When Jcd/|Jab|takes the value of 0.2,the -ΔS is observed to be 0.033 75,while the ΔTadis observed to be 0.004 25.Moreover,the ΔTadcurve tends to decline with the increase of T/|Jab| more obviously than the -ΔS curve.
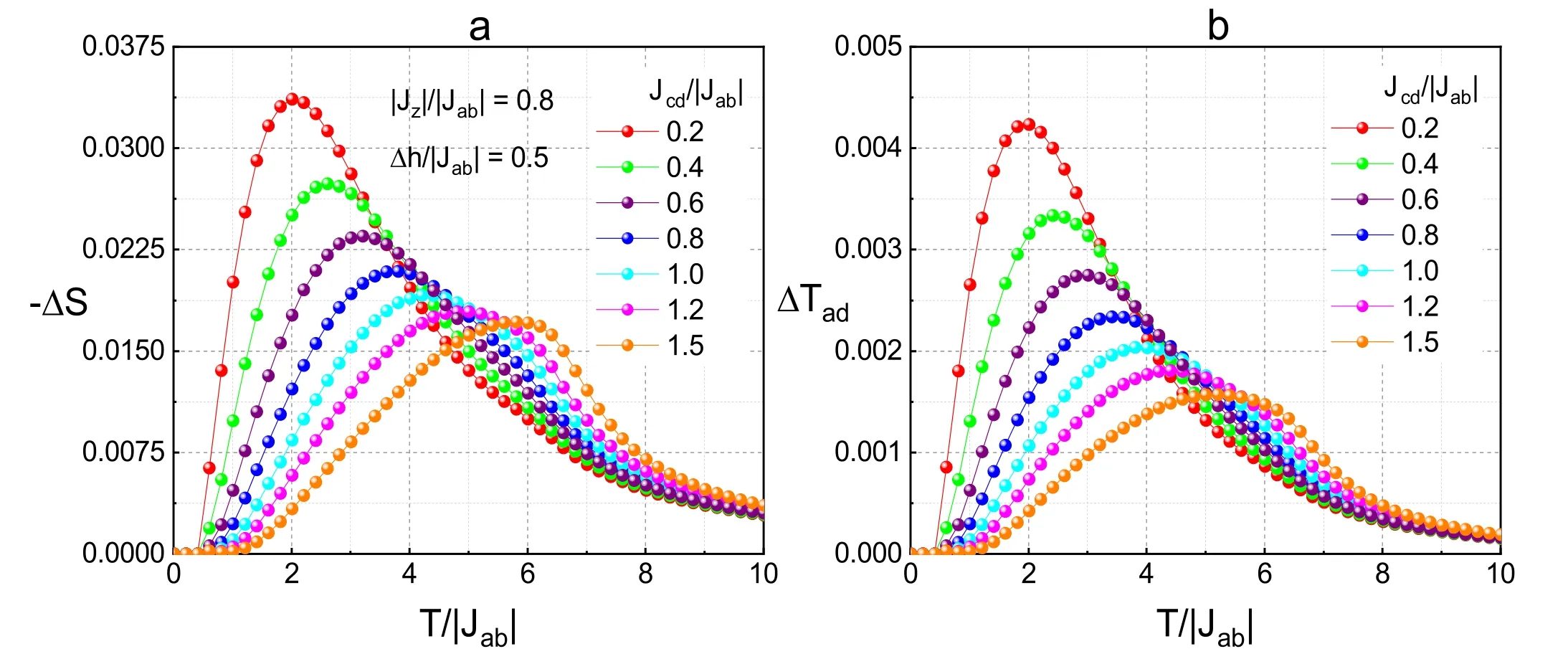
Figure 5.The a) -ΔS and b) ΔTad as a function of T for various Jcd/|Jab| with fixed |Jz|/|Jab|=0.8 and h/|Jab|=0.5.
The-ΔS and ΔTadof the bilayer system under the effect of|Jz|/|Jab|for fixed Jcd/|Jab|=1.2,Δh/|Jab|=0.5 is shown in figure 6.In figure 6(a),each curve has a maximum,and the temperature corresponding to it is in the vicinity of TC.The location of the maximum shifts to the high temperature region as |Jz| increases.The value of it can be seen as 0.026 when|Jz|/|Jab|=0.2.Figure 6(b) presents the maximum moves to the high temperature region with the increase of|Jz|/|Jab|,and it can reach 0.0028 for |Jz|/|Jab|=0.2.
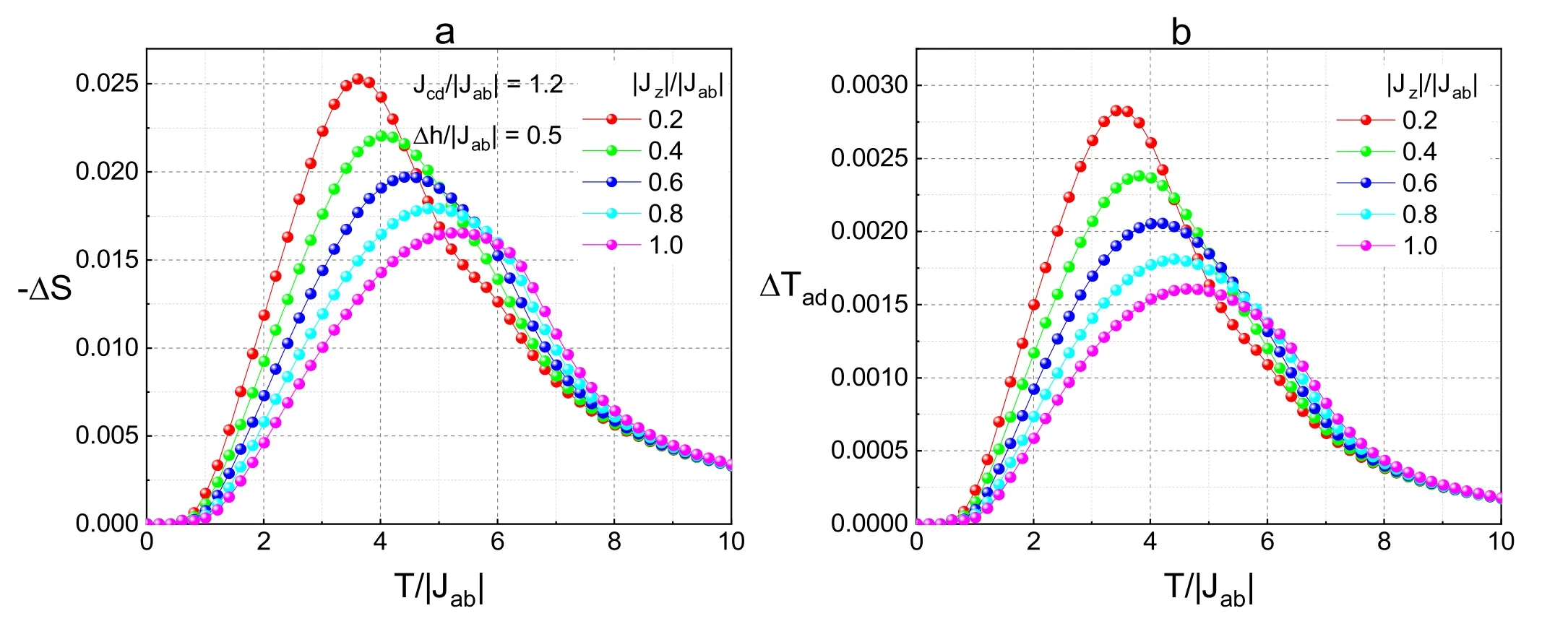
Figure 6.The a) -ΔS and b) ΔTad as a function of T for various |Jz|/|Jab| with fixed Jcd/|Jab|=1.2 and h/|Jab|=0.5.
All the results regarding the properties of the bilayer system are simulated in the presence of an external magnetic field,so it is of great necessity to investigate the dependence of -ΔS and ΔTadon the Δh,which is displayed in figure 7.Figure 7(a) gives the -ΔS as a function of Δh and T.The other parameters are selected as Jcd/|Jab|=1.2,|Jz|/|Jab|=0.8,respectively,and this figure shows us an intuitive phenomenon that when T changes from 6.0 to 9.8,there exists the maximum and it increases as Δh changes from 3.25 to 4.0.Figure 7(b)presents the ΔTadas a function of Δh and T.The maximum of the curves can be seen when T changes from 4.5 to 8.8,and it increases with the enlargement of Δh.Some comparisons may be implemented between these results and other studies,which investigated the influence of an external field on the -ΔS and ΔTadof the system[14,31,34,35,37,38].
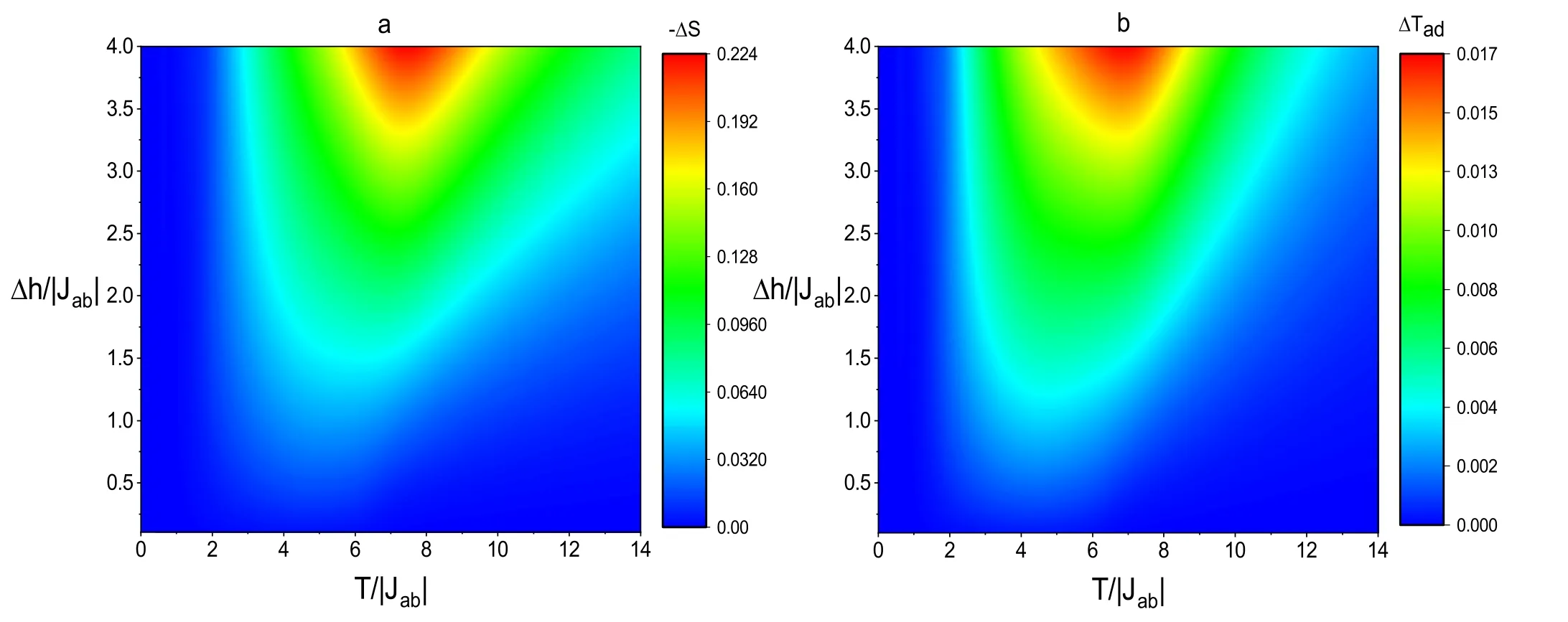
Figure 7.The phase diagram of the a) -ΔS and b) ΔTad under the effects of Δh and T for Jcd/|Jab|=1.2,|Jz|/|Jab|=0.8.
The relative cooling power (RCP) is a significant physical parameter to elucidate the character of the MCE.As given in figure 8,the Δh dependence of RCP corresponds to different values of exchange couplings—figure 8(a) for Jcd/|Jab|=0.6,1.2,and figure 8(b)for|Jz|/|Jab|=0.2,0.8.It can be seen from figure 8(a) that RCP increases monotonously and smoothly as the field Δh increases,and can reach values of 2.00 and 1.75 for Jcd/|Jab|=0.6 and 1.2,respectively.Similar results can be seen in [31,36,38],and RCP decreases gradually with the increase of Jcd/|Jab| for a certain Δh.A similar phenomenon in figure 8(a) can also be seen in figure 8(b)—that is,RCP goes smoothly with the increase of Δh,and the large |Jz|/|Jab| corresponds to the small RCP.Therefore,a conclusion can be drawn that weakening the exchange coupling and heightening the external magnetic field can contribute to magnifying the RCP of the system and make the material a better candidate for a magnetic refrigerant.This conclusion is in accordance with[34,37,40].
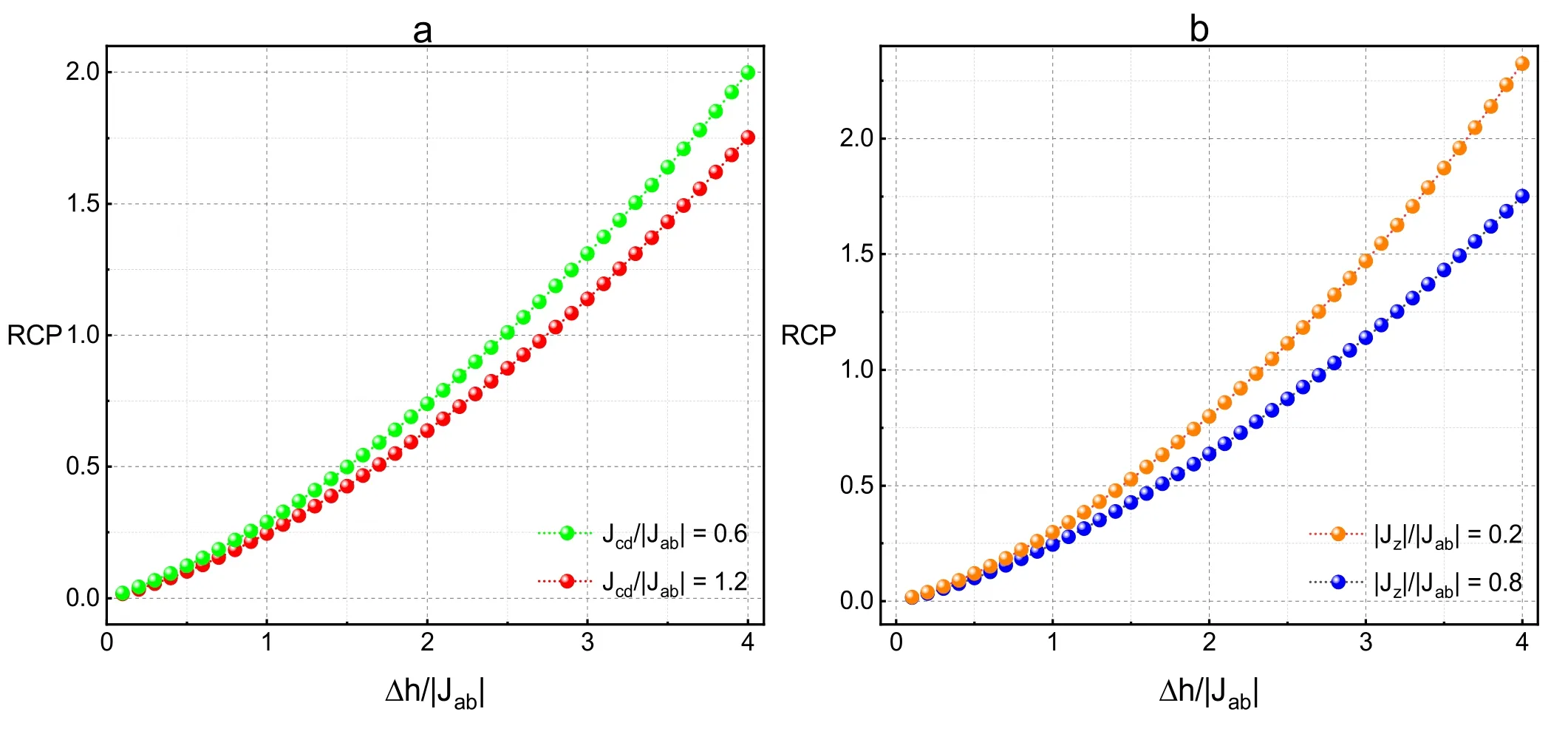
Figure 8.The influence of h on the RCP(a)for various Jcd/|Jab|=0.6,1.2 with fixed|Jz|/|Jab|; (b)for various|Jz|/|Jab|=0.2,0.8 with fixedJcd/|Jab|=1.2.
3.3.Hysteresis loops
In this subsection,we discuss the hysteresis loops of the system under the influence of exchange couplings,and the temperature dependence of the hysteresis loop is also presented.Figure 9 presents the magnetization as a function of the external magnetic field h for different values of Jcd/|Jab|with|Jz|/|Jab|=0.8,T=0.05.Only one loop can be seen and the area of the loops gets wider with Jcd/|Jab| changing from 0.1 to 2.1.It is reasonable that the coercive field and the residual magnetization augment with the increase of exchange coupling.This action originates from the enlargement of the exchange interaction energy.An analysis of these results shows that the present AFM/FM BiFeO3/Co can exhibit some properties similar to those found in ferromagnetic materials [60,61].
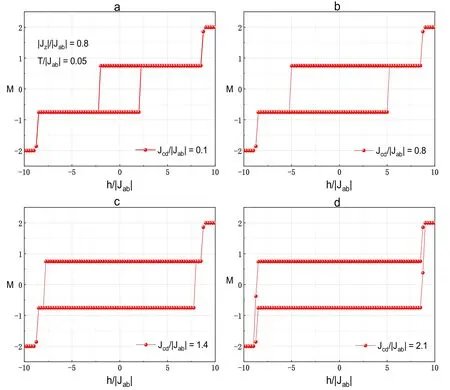
Figure 9.The hysteresis loops of the system for different values of Jcd/|Jab|with|Jz|/|Jab|=0.8,T/|Jab|=0.05,a)Jcd/|Jab|=0.1,b)Jcd/|Jab| = 0.8,c) Jcd/|Jab| = 1.4,d) Jcd/|Jab| = 2.1.
Analogically,figure 10 displays the magnetization as a function of the external magnetic field h for various values of|Jz|/|Jab|with Jcd/|Jab|=1.2,T=0.05.Similarly,the increase of|Jz|/|Jab|is not advantageous for the number of hysteresis loops,but it is beneficial for the increase of the area for the loops.
Finally,the impact of temperature on the hysteresis loop with the parameter Jcd/|Jab|=1.2,|Jz|/|Jab|=0.8 is shown in figure 11.From the figure,we can see that the remaining magnetization and the coercive field decrease gradually as T changes from a lower value to a larger; eventually,the loop vanishes at T=6.5,corresponding to the critical temperature.Similar phenomena have also been found in the investigations of nanoislands [62,63],graphene-like quantum dots [64],laddertype graphene nanoribbons[65],a graphene monolayer[66]and triple-layer[67]as well as other magnetic nanosystems[68–72].
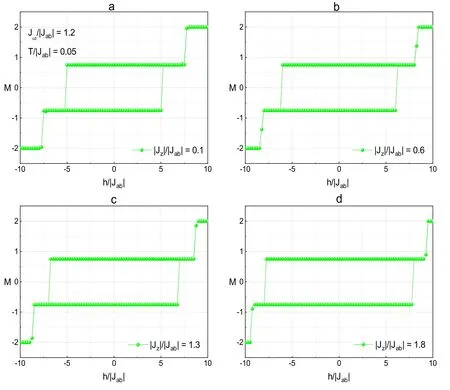
Figure 10.The hysteresis loops of the system for different values of|Jz|/|Jab|with Jcd/|Jab|=1.2,T/|Jab|=0.05,a)|Jz|/|Jab|=0.1,b)|Jz|/|Jab| = 0.6,c) |Jz|/|Jab| = 1.3,d) |Jz|/|Jab| = 1.8.
4.Conclusion
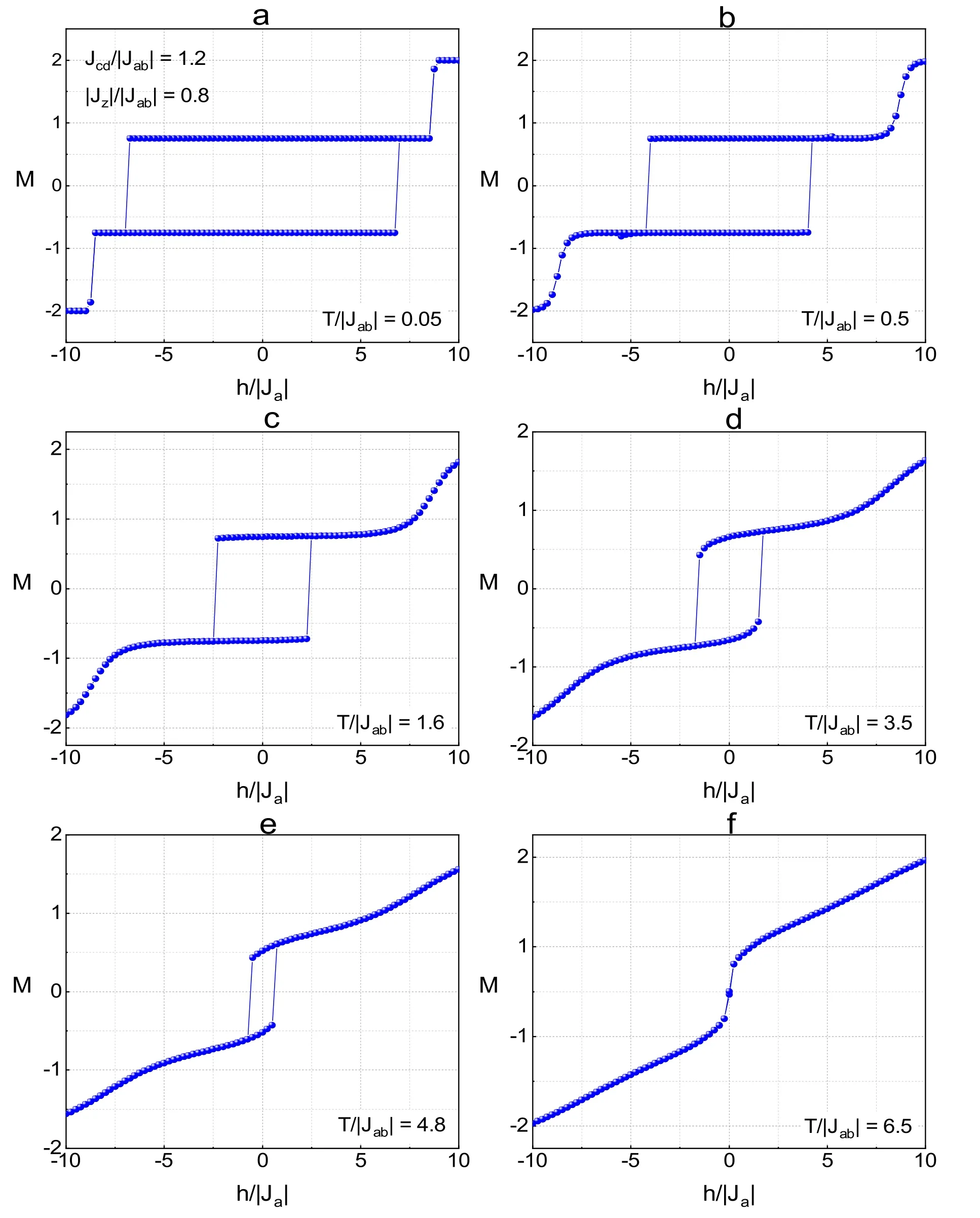
Figure 11.The hysteresis loops of the system for different values of T/|Jab|with Jcd/|Jab|=1.2,|Jz|/|Jab|=0.8,a)T/|Jab|=0.05,b)T/|Jab|= 0.5,c) T/|Jab| = 1.6,d) T/|Jab| = 3.5,e) T/|Jab| = 4.8,f) T/|Jab| = 6.5.
The magnetic properties,magnetocaloric effect as well as hysteresis behaviors have been investigated and predicted for a mixed-spin (5/2,3/2) AFM/FM Ising BiFeO3/Co bilayer applying the Monte Carlo method.The results show that either exchange coupling or an external magnetic field has an important influence on the magnetic properties and the magnetocaloric effects.The presence of Jcd,|Jz|and h causes the system to undergo a rough process to accomplish phase transition,while the decrease of Jcd,|Jz|,and the increase of h has a significant advantage in increasing the values of Δh,ΔTad,and RCP.Furthermore,the larger Jcdand |Jz| are beneficial for the enlargement of the area for the hysteresis loops.These results indicate that the BiFeO3/Co bilayer has appropriate properties to be a suitable candidate for use as a magnetic refrigerant material.We hope the study that we have implemented can provide direction for experimental research and theoretical reference for other works.It can be remarked that,although much effort has gone into the magnetic and electric properties of the BiFeO3/Co bilayer,there is still much more to do,such as dynamic magnetic properties as well as the effect of atom doping,which will be investigated in detail in the future.
杂志排行
Communications in Theoretical Physics的其它文章
- Electron Acceleration by a radially polarised cosh-Gaussian laser beam in vacuum
- The continuous wavelet derived by smoothing function and its application in cosmology
- Joule–Thomson expansion of RN-AdS black hole immersed in perfect fluid dark matter
- The collision frequency of electron-neutralparticle in weakly ionized plasmas with non-Maxwellian velocity distributions
- Quantum corrections to the entropy in a driven quantum Brownian motion model
- Grüneisen ratio quest for self-duality of quantum criticality in a spin-1/2 XY chain with Dzyaloshinskii–Moriya interaction
