具变系数的非局部高阶Kirchhoff方程的整体吸引子族

吕鹏辉， 林国广， 孙玉婷

(1. 苏州大学应用技术学院， 江苏 苏州215325)

(2. 云南大学数学与统计学院， 云南 昆明650500)

(3. 陆军边海防学院昆明校区， 云南 昆明650207)

1 引言

设Ω⊂RN是具有光滑边界的有界区域， 本文主要研究Ω 上具有变系数非局部高阶Kirchhoff方程的渐近行为:

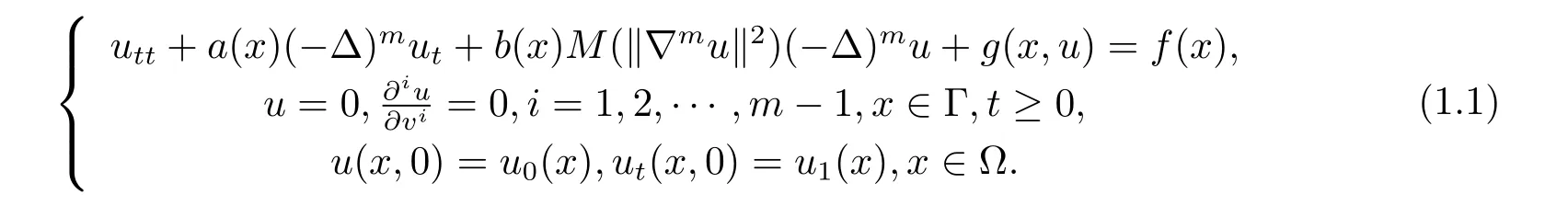
其中Γ 为Ω 的光滑边界，v是边界Γ 上的外法向量，m ＞1，a(x)，b(x) 为关于空间变量x的变系数函数，f(x) 是外力项，g(x，u) 是满足一定增长条件和耗散条件的关于未知函数u的非线性源项.

一般而言， 整体吸引子是一个具有不变性的非空紧集， 并且能够吸引任何有界集. 对于耗散动力系统， 整体吸引子是解释系统解的长时间动力学的核心概念， 对于自治动力系统， 通常用整体吸引子来刻画其渐近行为.

吸引子包含了系统几乎所有的长时间信息， 因此关于吸引子存在性及结构的研究对整个系统的长时间演变过程有着非常重要的意义. Kirchhoff方程作为一重要的数学物理方程， 研究其吸引子就显得相当重要， 近年来， 得到了许多有关Kirchhoff型方程的长时间动力学行为，I.Chueshov[1]研究了带非线性强阻尼Kirchhoff方程utt-σ(‖∇u‖2)Δut-φ(‖∇u‖2)Δu+f(u) =h(x) 的长时间动力行为. Guoguang Lin， Penghui Lv 和Ruijin Lou[2]研究了具阻尼项的广义非线性Kirchhoff-Boussinesq 方程的整体动力学， 研究得到了该类方程的整体吸引子和指数吸引子. 更多有关低阶波动方程或Kirchhoff方程的研究可见文献[3-5].

随着研究的深入， 学者开始研究高阶波动方程的长时间动力学行为. Salim A. Messaoudia ， Belkacem Said Houari[6]研究了具有Dirichlet 边界条件的多维高阶Kirchhoff方程， 估计了在正初始能量下解爆破. 林国广， 李卓茜[7]研究了一类非线性非局部且具强阻尼项的高阶Kirchhoff方程的初边值问题， 得到了该类高阶方程的整体解的存在唯一性， 并且得到了该类Kirchhoff方程的整体吸引子族， 且整体吸引子族具有有限的Hausdorff维数和Fractal 维数. Fucai Li[8]研究了有界域上具有非线性耗散的高阶Kirchhoff型方程

其中m ＞1，q，p，r ＞0. 当p ≤r时， 得到方程的整体解， 同时当p ＞max{r，2q}时， 对于所有具负初始能量的初始数据， 解在Lp+2范数下将有限时间内爆破. 详细的关于更多高阶Kirchhoff方程的相关研究可见文献[9-11].

目前带变系数的高阶Kirchhoff方程的渐近行为见文较少. 本文在得到问题(1.1) 的渐近行为时， 主要的问题是如何处理变系数， 在变系数情况下如何得到渐近紧性. 本文运用合理的假设和莱布尼兹公式克服了变系数带来的困难， 进而得到有界吸收集和渐近紧性.

本文第2 部分介绍有关概念和动力系统的相关定义及理论; 第3 部分得到问题的先验估计和整体解; 第4 部分得到问题(1.1) 的整体吸引子族.

2 预备知识

本节主要给出动力系统和整体吸引子(族) 的相关理论.

首先引进本文需用到的相关记号:

定义H=L2(Ω) 上的内积和范数分别为(·，·) 和‖·‖，Lp=Lp(Ω)，‖·‖p=‖·‖Lp， 其中p ≥1.现令

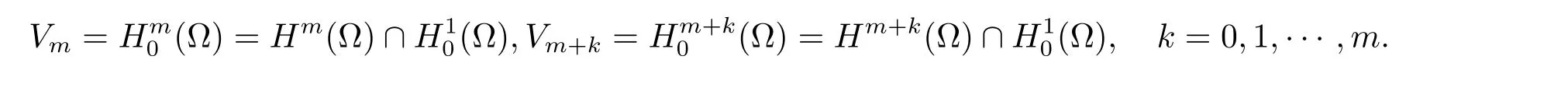
其相应的内积和范数分别为特别地， 当t →∞时， 从u0出发的一切轨道S(t)u0收敛于A0内， 即有dist(S(t)u0，A0)→0(t →∞)， 则称紧集A0为半群{S(t)}t≥0的整体吸引子.

引理2.3[7]设X是Banach 空间， 连续的算子半群{S(t)}t≥0满足

(1) 半群{S(t)}t≥0在X中一致有界， 即∀R ＞0 存在正常数C(R) 使得‖u‖X ≤R， 有

(2) 存在X中有界吸收集B0， 则任意一个有界集B ⊂X， 存在一个时刻t0， 使得

(3) 对t ＞0，S(t) 是全连续算子;

则半群{S(t)}t≥0具有紧的整体吸引子A0.

定义2.4 (整体吸引子族) 设Xk，k=1，2，···，m， 是Banach 空间，{S(t)}t≥0为连续的算子半群， 如果紧集Ak ⊂Xk满足

(1) 不变性 在半群{S(t)}t≥0作用下为不变集， 即S(t)Ak=Ak(∀t ≥0);

(2) 吸引性Ak吸引Xk中一切有界集， 即∀Bk ⊂Xk为Xk中的有界集， 有

特别地， 当t →∞时， 从u0出发的一切轨道S(t)u0收敛于Ak内， 即有dist(S(t)u0，Ak)→0(t →∞)， 则称紧集Ak为半群{S(t)}t≥0的整体吸引子族.

引理2.5 设Xk，k=1，2，···，m， 是Banach 空间， 连续的算子半群{S(t)}t≥0满足

(1) 半群{S(t)}t≥0在Xk中一致有界， 即∀R ＞0 存在正常数Ck(Rk) 使得‖u‖Xk ≤Rk，有

(2) 存在Xk中有界吸收集B0k， 则任意一个有界集B ⊂Xk， 存在一个时刻t0k， 使得

(3) 对t ＞0，S(t) 是全连续算子;

则半群{S(t)}t≥0具有紧的整体吸引子族Ak.

3 整体解的存在性

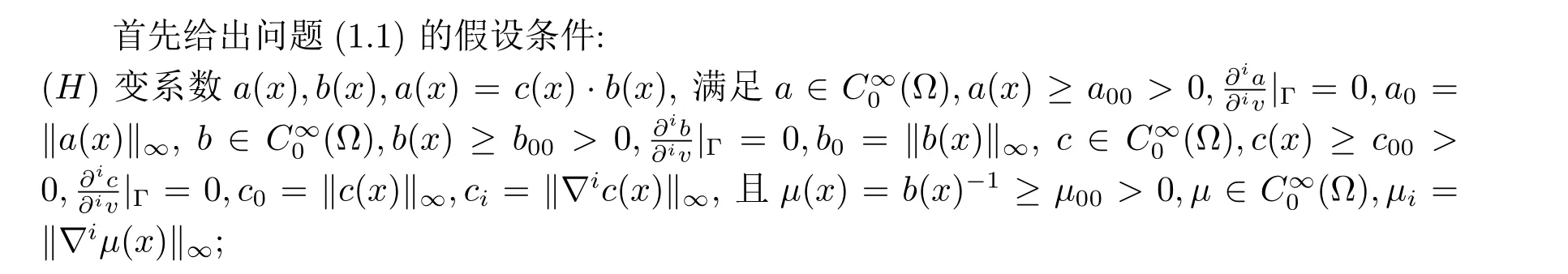
(M)M ∈C1(R+)， 且0＜M0≤M(s)≤M1，∀s ∈R+，x ∈Ω，k= 0，1，···，m， 非线性项g(x，u) 满足下列条件: 存在正常数β1，β2，β3，β4，β5＞0， 对∀u ∈R，x ∈Ω， 满足

其中v=ut+εu. 且存在一个正常数R0和t0＞0， 使得

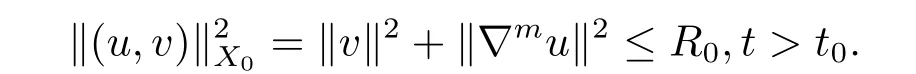
证 将v与方程组(1.1) 在L2(Ω) 中作内积， 得

分别处理(3.9) 中各项:

因此， 存在一个正常数R0和t0＞0， 使得

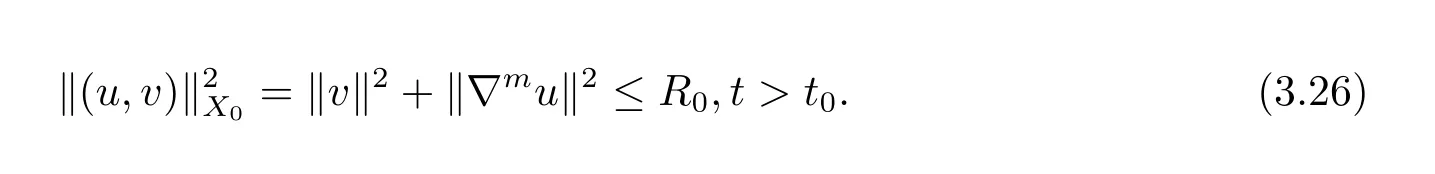
引理3.1 证毕.

引理3.2 设(H) 成立，M满足(M)，f ∈Vk， (3.1)-(3.5) 成立， (u0，u1)∈Xk，k=1，2，···，m， 由问题(1.1) 确定的(u，v) 满足

引理3.3 (整体解的存在唯一性) 在引理3.1 和引理3.2 假设条件下， (u0，u1)∈Xk，k=0，1，···，m， 则初边值问题(1.1) 存在唯一的整体解(u，v)∈L∞([0，+∞)，Xk).

证 存在性 利用Galerkin 方法证明整体解的存在性.

第一步， 近似解构造

满足初始条件un(0)=un0，unt(0)=un1， 当n →+∞时， 在Xk中(un0，un1)→(u0，u1)， 由常微分方程的基本理论可知近似解un(t) 在(0，tn) 存在.

第二步， 先验估计

现需证明Xk(k= 0，1，···，m) 空间解的存在在性， 故在(3.45) 两端同时乘以λkj(h′j(t)+εhj(t))， 并对j求和， 令vn(t)=unt(t)+εun(t).

由引理3.1 和引理3.2 得

当k=0 时， 得到X0空间中解的先验估计

由此可知， (un，vn) 在L∞([0，+∞);X0) 中有界， (un，vn) 在L∞([0，+∞);Xk) 中有界.第三步， 极限过程

在Xk，k=0，1，···，m空间中， 从序列un中选取子列， 仍用un表示， 则

在L∞([0，+∞);Xk) 中弱* 收敛.

由Rellich-Kohdrachov 紧嵌入定理知Xk(k= 1，2，···，m) 紧嵌入X0， 有(un，vn)→(u，v)

在X0中几乎处处强收敛.

由(3.48) 得

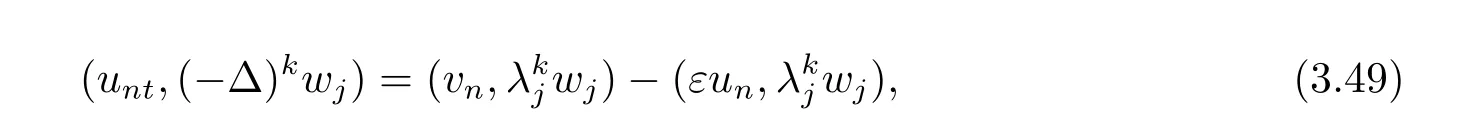
从而解的唯一性得证.

4 整体吸引子族的存在性

定理4.1 在引理3.1 和3.2 的假设条件下及引理3.3， 问题(1.1) 存在整体吸引子族:

定理4.1 证毕.