Sturm-Liouville 算子的一维奇异扰动的逆特征值问题

吴雪雯

(西北工业大学数学与统计学院， 陕西 西安710072)

1 引言

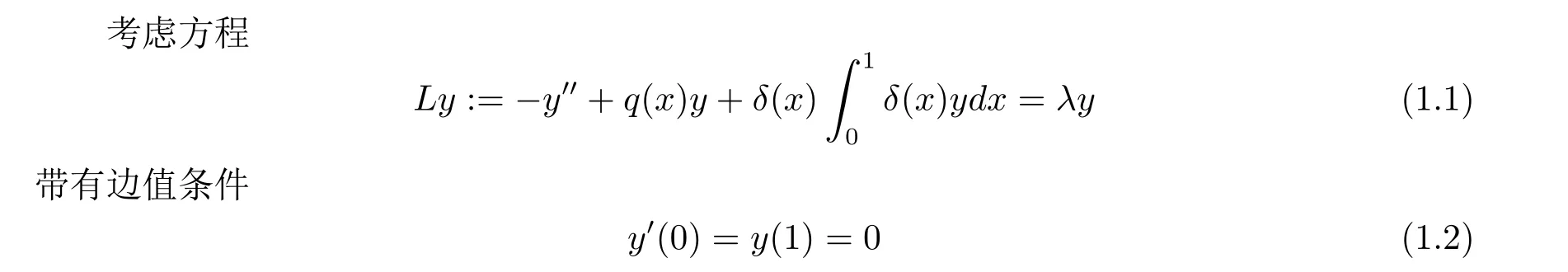
其中q(x)∈L2(0，1)，δ(x) 是狄拉克函数. 这里算子L是自伴的并且是Sturm-Liouville 算子L0y:=-y′′+q(x)y带有边值条件(1.2) 的一个一维奇异扰动. 由文献[1] 知， 算子L0在L2(0，1) 上是自伴的且下半有界， 它的谱由特征值组成.

本文的目的是通过运用Sturm-Liouville 算子的逆谱理论(见文献[1])， 由算子L0及L的谱重构(1.1) 中的势函数q(x). 然而， 方程(1.1) 的初值问题无法直接解出. 结合文献[2] 中的方法， 我们研究的逆问题可以由Sturm-Liouville 算子的逆谱理论有效地解决.

Sturm-Liouville 算子的一维扰动的谱问题[2-5]中已有所研究. 关于逆问题， 扰动项是属于L2(0，1) 中函数的算子已被考虑过， 例如文献[6， 7]. 由文献[2]， 我们知道扰动项的函数可以为奇异函数. 我们的文章考虑的算子L0的扰动项是δ(x). 通过运用文献[2] 中的方法， 我们得到了算子L的特征值函数， 这为我们之后考虑的逆问题提供了一个必要的准备. 关于其它的Sturm-Liouville 算子的一维扰动的逆问题， 见文献[8， 9].

本文的主要结论是， 已知算子L0的谱为{λn}∞n=0， 如果一列实数列{μn}∞n=0满足一个交替性质及渐近式， 则存在势函数q(x) 使得算子L的谱是{μn}∞n=0. 下一节我们将陈述这个主要结论及证明， 并且给出重构q(x) 的具体算法.

2 预备知识

首先我们提及一些需要用到的预备知识， 参见文献[2， P8-10].

引入关于算子L0的如下的线性赋范空间H±1(L0). 定义H+1(L) 是D(L1/2) 以

为范数的线性赋范空间， 易知，H+1(L0) 是完备的;H-1(L) 是L2(0，1) 以

3 主要结论及其证明