单纯形上二次型函数的最值搜索算法
2021-10-12李光辉李俊鹏
李光辉,李俊鹏
(凯里学院理学院,贵州 凯里 556011)
1 引言
在许多实际问题中都会遇到求解二次型函数全局最值的问题,由于受到各种条件的限制,有时需要求解二次型函数在一些特殊约束下的最值.随着科学技术的发展,人们所遇到的二次型优化问题也越来越复杂.由于约束区域与函数向量都更为复杂,所以难以用统一的数学公式给出最优化结果的显示表达.
约束域上二次型的优化问题有着广泛的应用,例如,文献[1-2]都使用算法搜索出在一些特殊区域上的二次型的全局最值.著名的Cramér-Rao不等式就是根据二次型下界所确定的,文献[3]中第4章详细讨论了这一问题.文献[4-5]介绍了关于二次型优化在其他领域中的应用.在特殊的约束条件中,单纯形是一类常见的约束域,它是由q维空间中q个线性无关的点z1,z2,···,zq∈Rq所围成的区域,将这一区域记为


的最值问题.
在单纯形约束域上求解二次型最值问题有着重要的背景.例如,在混料试验设计中,为了判断一个设计是否为最优,可以通过二次型优化确定其方差函数在约束域上的最值,从而得到结论.关于混料设计中方差函数的优化问题可以参见文献[6-7].
鉴于此,本文研究在单纯形域上二次型的优化问题,构造了在单纯形域上搜索二次型最值的两类算法.这两类算法都能实现任意的函数向量所确定的二次型在单纯形上的全局最值搜索.本文首先介绍单纯形上二次型函数的定义;第2节构造了一类适用于单纯形上二次型优化的Newton-Raphson算法;第3节讨论了随机搜索算法在搜索二次型函数最值的应用;第4节通过模拟试验说明这类算法的有效性;最后提出可进一步研究的问题.
2 单纯形上的Newton-Raphson算法
由于形如(1)式中的q维空间的单纯形可以通过线性变换为标准单纯形

即对于任意的单纯形都可以表示为

的形式.所以本文主要讨论在Sq−1上的二次型优化问题.设D是m阶实对称矩阵,需要优化的模型为

其中f(x)=(f1(x),f2(x),···,fm(x))T是已知的函数向量.
Newton-Raphson算法的基本思想是由某一点x(0)∈Sq−1的梯度方向确定最优步长t,使得下一步迭代值x(1)=x(0)+t·∇Φ(x(0);D)能使得 Φ(x;D)达到最大 (或最小),这里∇Φ(x(0);D)表示x(0)点处的梯度向量.下面从梯度搜索方向与边界点搜索两方面讨论.
为了使得x(0)点下一步搜索方向的向量必须与Sq−1共面,考虑将x(0)处的梯度投影在单纯形上.因为二次型函数Φ(x;D)在任意一点x∈Sq−1的梯度向量为

则过x0=(x01,x02,···,x0q)T且方向与∇Φ(x0;D)一致的直线为

则直线l1上任意点x在Sq−1上的投影可表示为,其中

表示由x指向x′的向量,其中Iq为q阶单位阵,,1q是元素全为1的q维列向量.
显然对于任意的t∈R都有‖gp(t;x0)‖=0,即gp(t;x0)与单纯形Sq−1是共面的,所以在x0处沿gp(t;x0)移动的点始终位于Sq−1上.gp(t;x0)就是x0点的梯度向量在单纯形上的投影,通过控制参数t可以确定下一步迭代的最优解,即下一步迭代点与x0之间存在形如x=x0+gp(t;x0)的关系.下面讨论边界点搜索的问题.
由于当x0点位于Sq−1的边界时,下一步迭代的最优解往往会超出Sq−1.为了更好地实现在边界上的搜索,设立一个松弛变量ε>0,令

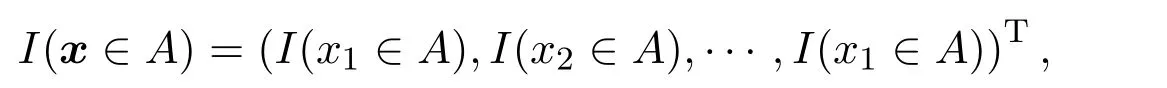
其中I(·)为示性函数.记I+=I(x>1),I−=I(x<0).对于任意点,如果x中所有大于 0的分量为xi1,xi2,···,xik,令,j=1,2,···,k.定义变换系数

令γ=(γ1,γ2,···,γq)T,定义在边界上搜索的函数为
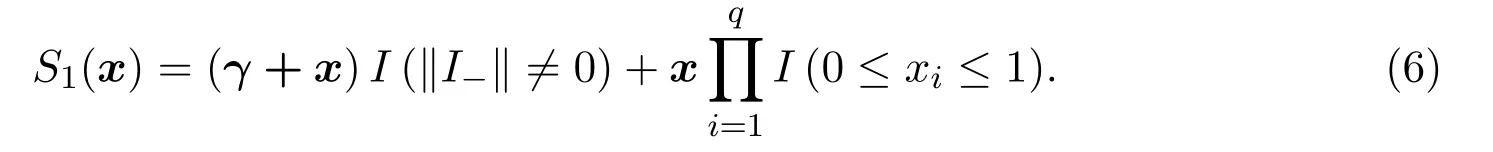
称(6)式中的S1(x)为I型贴边函数,其功能主要是将超出Sq−1的点沿梯度投影在边界上.由于二次型函数(3)在Sq−1上往往会呈现出多峰的形态,所以为了搜索出全局最值点,可以考虑同时投入若干个初值点,同时进行搜索,每个点经过形如(4)式的迭代称为一步搜索,将所有点都经过一步搜索的过程称为一轮搜索.以搜索二次型函数最大值为例,将搜索过程整理为以下算法.

算法1: 单纯形上的Newton-Raphson算法输入:迭代初值x(0)1,x(0)2,···,x(0)n 以及松弛变量 ε>0 1: For j=1 to N 2: For i=1 to n 3: 确定常数a(j)i≥0使得x(j)i+gp(t;x(j)i)∈Sq−1ε成立4: t(j)i−opt=arg max 0≤t≤a(j)i{Φ(x(j)i +gp(t;x(j)i))}5: x(j+1)i =S1(x(j)i +gp(t(j)i−opt;x(j)i))6: End for 7: End for
3 单纯形上的随机搜索算法
根据文献[8]的思想,首先构造单纯形区域上的均匀分布的随机点集,然后将其映射到一个子区域,从中选取最优点作为迭代的下一步,以此类推,直到所有点都固定.以下从随机点的产生与迭代过程的进行两方面进行讨论.
为了使得搜索效率更高,本文采用单纯形格点集混合均匀分布的随机点集作为备选点集.根据文献[9]中所介绍的在单纯形上生成均匀分布的随机点集的方法,可以令矩阵
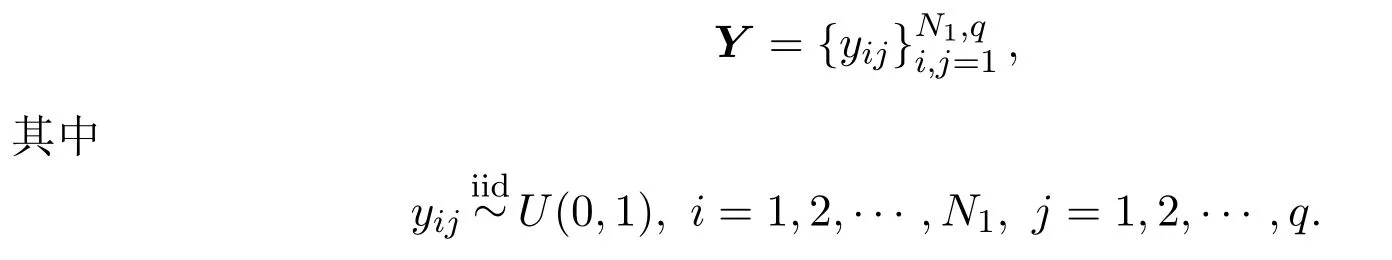

以搜索二次型函数最大值为例,将以上搜索过程整理为以下算法.

算法2: 单纯形上的随机搜索算法输入:迭代初值x(0)1,x(0)2,···,x(0)n,拟分量变换参数序列 λ(M)<···<λ(2)<λ(1),松弛变量ε>0,固定格点集T2=L(q,m).1: For j=1 to M 2: For i=1 to n 3: 产生服从单纯形上均匀分布的随机点集,并按行排列为T(j)1 ~ U(Sq−1)4: T(j+1)C =C([T(j)T 1 ,TT2]T,x(j)i ,λ(j))5: T(j+1)=■■ x(j)i T(j+1)C■■,并记T(j+1)为T(j+1)中各行为点构成的集合6: x(j+1)i =argmax x∈T(j+1)Φ(x)7: End for 8: End for
经过M轮搜索后,会驻留在Φ(x;D)的各个子区域的最值处.
4 模拟实例
本节使用两种算法搜索三分量二次型函数 Φ(x)=fT(x)Mf(x)−6在S3−1上的最大值,其中f(x)=(x1,x2,x3,x1x2,x1x3,x2x3)T,使用 3分量 2阶格子点集L{3,2}={z1,z2,···,z6}.并令

Φ(x)的曲面图如图1(a)所示.
使用两种算法搜索Φ(x)在S3−1上的最大值.首先在S3−1中产生100个均匀分布的随机点作为初值.使用算法1,取松弛变量ε=0.1,经过 35轮迭代即可得到最优解.

图1 (a)二次型曲面图;(b)算法1搜索过程Φ(x)迭代值;(c)算法2搜索过程Φ(x)迭代值
不论使用哪种算法,最终搜索得到的最值点都相同,100个初值最终都重合到7个点处,分别是S3−1上的3个顶点z1=(1,0,0),z2=(0,1,0),z3=(0,0,1)和三个棱中点z4=(0.5,0.5,0),z5=(0.5,0,0.5),z6=(0,0.5,0.5).从图1(a)中也可见,z0是Φ(x)函数的一个极大值点.算法1之所以会确定该点是因为搜索过程中,在该点处的梯度向量始终为0,所以后续的迭代都无法进行.算法2则是因为该点是极大值点,在以该点为中心的一个子单纯形领域内,再无法产生使得函数值更大的备选点.所以,这两类算法不仅可以搜索得到二次型函数在单纯形域上的全局最值,还可以搜索出各个极值点.
5 讨论
通过实例可以验证这两种算法的有效性,并且这类算法对于单纯形域上的其他函数也同样适用.一般的,如果Φ(x)在任一点x∈Sq−1处的梯度都存在,那么使用算法1的收敛速度会更快.而如果Φ(x)形式复杂,梯度向量没有显示表达,则使用算法2更为稳健.总体而言,算法2易于实施,不用关心迭代点的搜索方向,只考虑备选点集分布的均匀性即可.
此外,如果搜索区域是单纯形内部的一个子区域,特别当约束条件过多,区域形式较为复杂的时候,如何在边界上执行搜索过程就是一个难题,并且对于初值的选取十分敏感.为此,可以考虑在约束区域内产生均匀足够高阶的格子点集,并且使得这个格子点集合能够包含这一区域各个顶点与棱中点,由此可以确定出一组较好的搜索初值.
这两类算法在单纯形上的二次型函数的搜索是十分有效的,如果约束过多,函数复杂,使用算法2来搜索函数最值是比较有效的方法.
