基于逆溶解度性质的硫酸钠-水体系成核动力学的研究

王彦飞，焦 健，蒋淑婉，许史杰

（天津科技大学化工与材料学院，天津市卤水化工与资源生态化利用重点实验室，天津300457）

硫酸钠主要用于制造水玻璃、玻璃、瓷釉、纸浆、制冷混合剂、洗涤剂、干燥剂、染料稀释剂、分析化学试剂、医药品、饲料等［1-2］。结晶是硫酸钠从水相中分离和纯化的主要步骤，本文通过实验确定其在水溶液中的介稳区数据，对理解成核现象和控制晶体尺寸分布具有重要的意义。文献上对于溶解度随温度增大而增大的物系（正溶解度）介稳区及成核动力学报道较多，但对于溶解度随温度增大而减小的物系（逆溶解度）的介稳区及成核动力学报道非常匮乏。在硫酸钠-水体系中，在不同的温度范围内，平衡的固相盐主要有两种稳定相，分别是无水硫酸钠和十水硫酸钠。当温度高于305.55 K时，平衡固相是无水硫酸钠；当温度低于305.55 K时，平衡固相是十水硫酸钠。本文在308.15 K到336.15 K范围内，通过聚焦光束反射测量技术（FBRM）测定硫酸钠在水中的介稳区宽度，考察了升温速率、饱和温度对硫酸钠结晶介稳区宽度的影响，揭示成核规律，为类似逆溶解度结晶过程的优化提供指导。

1 成核理论

根据经典成核理论，成核速率是由成核能量、频率因子和过饱和度所决定的［3-5］，这说明了介稳态的存在，也说明了控制成核过程的难度。在成核领域许多研究者对成核动力学做了大量的研究，相继提出不同的模型。

1.1 Nyvlt′s模型

1985年，Nyvlt提出了半经验模型用于描述结晶成核的行为，该模型因其简单性被广泛使用［6-9］：

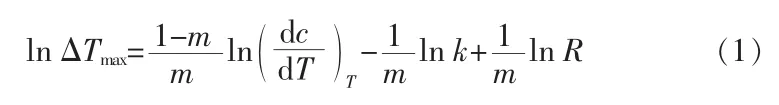
式中：dc/dT为t温度下溶解度的温度系数，mol/（L·K）；m为 表 观 成 核 级 数，k为 成 核 常 数。lnΔTmax与lnR成线性关系，斜率为1/m。Nyvlt′s模型的缺点是成核级数没有明确的物理意义，m是不确定的。

1.2 修正的Sangwal′s模型

2016年，Xu等［10］提出修正的Sangwal′s模型，该模型基于经典成核理论，即假设指前因子、表面能与降温速率和饱和温度是无关的，得到与饱和温度和成核温度无关的参数M和N。修正的Sangwal′s模型用下式表示：

式中：T0为饱和温度；ΔTmax为成核温度与饱和温度的差值；R为降温速率，K/h。

斜率N和截距M可以用下式表示：

式中：Rg为气体常数，8.314 5 J/（K·mol）；ΔHs为溶解焓，J/mol；f为成核速率与溶液过饱和度变化速率的比值；Vs为溶质的分子体积（对硫酸钠而言，Vs=8.80×10-29m3）；kb为玻尔兹曼常数（1.380 7×10-23J/K）；A为成核动力学相关的指前因子，其范围在1015～1042m-3·s-1；γ为晶核的表面能，mJ/m2。

研究发现，在给定加热速率下（T0/ΔTmax）2/（T0-ΔTmax）随ln［R/T0（T0-ΔTmax）］线性减小，斜率N为负。通过式（3）可以直接计算出界面能。之后通过式（5）和式（6）进一步计算出临界吉布斯自由能大小和临界核的大小：

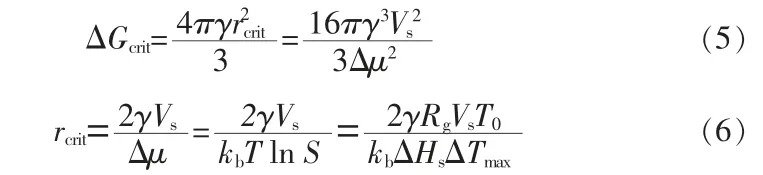
根据经典成核理论，稳态成核率可用式（7）表示：

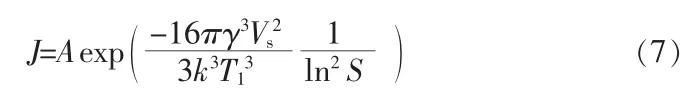
对于真实溶液，溶质浓度的比值（c1/c0）、饱和温度（T0）、成核温度（T1）和过冷度（ΔT）之间的关系可以用式（8）来表示：

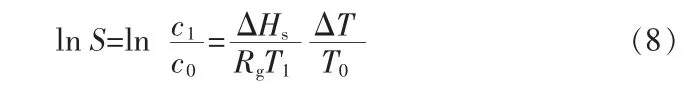
溶质在溶液里的化学势μl（J/mol）与溶质在固相里的化学势μs（J/mol）的化学势差值Δμ可以表示为：

因此等式（7）可以转化为下列表达式：

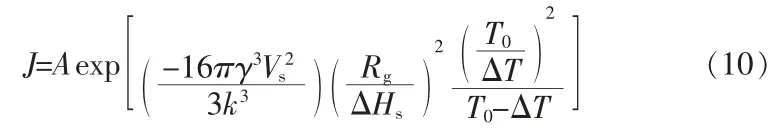
将上述修正的Sangwal′s模型用于硫酸钠升温结晶过程中的成核行为的描述，旨在探索升温速率以及饱和溶液温度与介稳区之间的关系，并揭示升温速率和溶液温度对成核固液界面张力和有效碰撞因子等成核参数的影响规律。

2 实验部分

2.1 实验试剂及仪器

实验试剂：硫酸钠（质量分数≥99.5%）；蒸馏水，电导率σ＜1×10-4S/m。

实验仪器：K6型Huber（加热制冷循环器）；iC FBRMTM型聚焦光束反射测量仪；CP114型精密分析天平；HD2004W型机械搅拌器；XD-2型X射线衍射仪。

2.2 介稳区宽度的测定

采用聚焦光束反射测量技术（FBRM）测定了硫酸钠的亚稳区宽度。把浓度已知的硫酸钠溶液降温至饱和温度T*以下5.00 K，搅拌速率定为600 r/min，恒温到溶液中没有晶体，再以一定升温速率加热，升温至FBRM数值发生骤变，把此刻的温度记为Tn。图1展示了FBRM数据伴随温度的变化。通过系列实验，获得硫酸钠在不同升温速率下的介稳区数据。

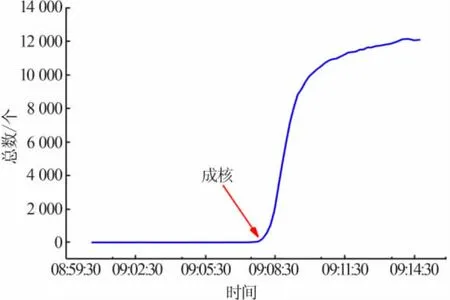
图1 在成核点处的FBRM数据Fig.1 FBRM data at the nucleation point

3 结果与讨论

3.1 溶解度数据模型关联

硫酸钠在水中溶解度数据报道较多，并经过验证是比较可靠的。所以本文直接采用文献［11］报道的硫酸钠在308.15～336.15 K下纯水中的溶解度。

对离散的溶解度数据点，采用Van′t Hoff方程来回归溶解度与温度之间的关系，结果如图2所示。方程形式见公式11，基于热力学方程，溶解熵ΔS和溶解焓ΔH可以根据拟合出来直线的截距和斜率求出。

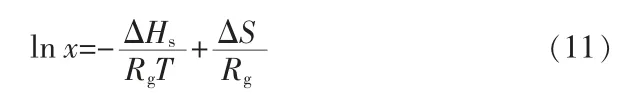
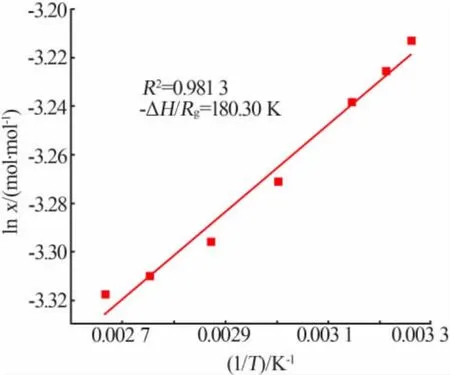
图2 Van′t Hoff方程拟合的溶解度数据Fig.2 Solubility data fitted by Van′t Hoff equation

3.2 不同条件对硫酸钠介稳区宽度的影响

在升温速率为2.0～35.0 K/h时，测定了不同饱和温度下（308.15、318.15、323.15、336.15 K）硫酸钠的介稳区数据，结果如表1所示。由表1可知，固定饱和温度不变时，升温速率越快介稳区越宽；保持升温速率恒定时，饱和温度越高介稳区越窄。

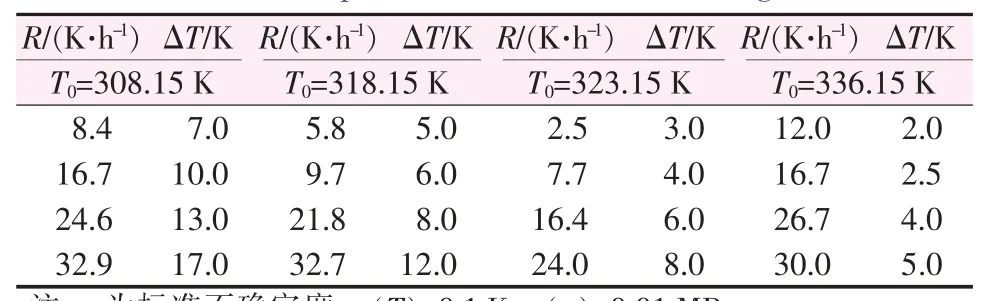
表1 不同饱和温度下和不同升温速率下硫酸钠的介稳区数据Table 1 Metastable zone data of sodium sulfate at different saturation temperature and different heating rates

3.3 成核参数的计算

为了描述硫酸钠-水体系介稳区在热力学和动力学影响下的变化规律，采用了Nyvlt′s模型和修正的Sangwal′s模型，分别如等式（1）、（2）所示。图3为升温速率和饱和温度与介稳区的关系。由图3可知，等式（1）很好地表达了lnΔT与lnR之间的线性关系。在Nyvlt′s模型中，可以用表观成核级数m来估计成核机理［12-13］。表2给出了Nyvlt′s模型拟合得到的不同饱和温度下硫酸钠在水中的成核级数。m值为1～2.5，说明硫酸钠-水体系的成核机理是爆发式的［14］。

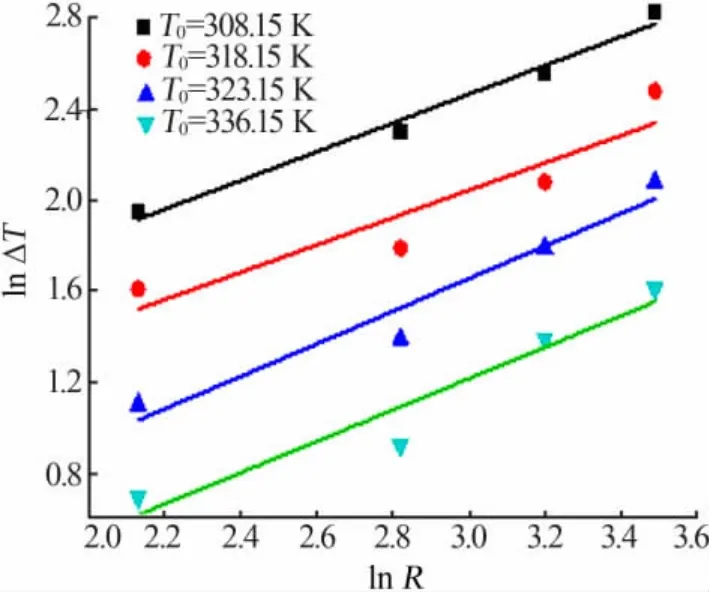
图3 升温速率和饱和温度与介稳区的关系Fig.3 The relationship between metastable zone and heating rate and saturation temperature

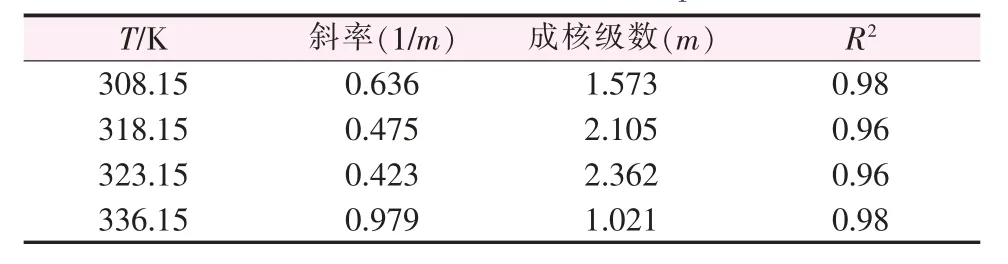
表2 不同饱和温度下用Nyvlt′s模型拟合获得的成核参数Table 2 Nucleation parameters obtained by fitting Nyvlt′s model at different saturation temperature

修正的Sangwal′s模型中有饱和温度和升温速率两个变量，这两个变量对介稳区的影响只能单独讨论。这就是在表3和表4中γ和A值存在差异的原因。表3和表4给出了相关动力学参数。表3中，饱和温度越低、表面张力越大，介稳区越宽；表4中，升温速率越快、表面张力越大，介稳区越宽。

表3 成核动力学参数值Table 3 Nucleation kinetic parameters

表4 不同饱和温度下的成核动力学参数值Table 4 Nucleation kinetic parameters at different saturation temperature

图4 和图5反映了成核过程中饱和温度与升温速率之间的相互作用。图4是在给定饱和温度下，升温速率对介稳区的影响趋势。在图4中，T02/ΔT2/T1与ln（R/T0/T1）服从线性关系，由图4可知，T0越大，直线越陡，这说明随着饱和温度的增加，升温速率对介稳区的影响越来越明显［15］。图5反映了饱和温度对介稳区的影响趋势。在图5中，T02/ΔT2/T1与ln（1/T0/T1）服从线性关系，由图5可知，随着升温速率的增加，抑制了饱和温度对硫酸钠介稳区的影响。

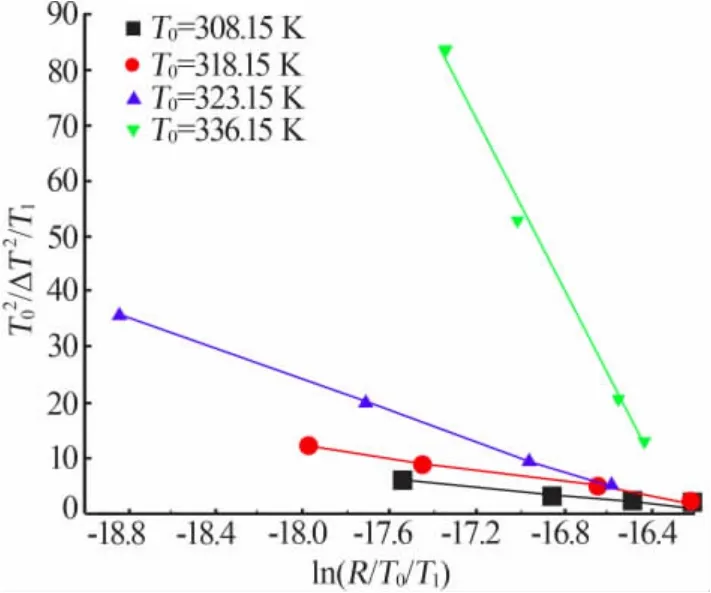
图4 给定饱和温度下升温速率与介稳区的关系Fig.4 The relationship between the heating rate and the metastable zone at the given saturation temperature

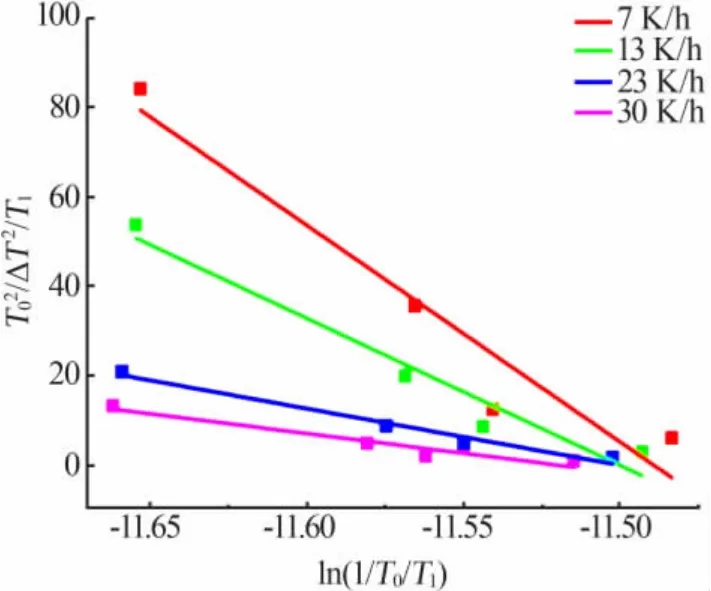
图5 给定升温速率下饱和温度与介稳区的关系Fig.5 The relationship between saturation temperature and metastable zone at the given heating rate

3.4 成核动力学行为描述

如图6所示，表面张力与饱和温度是负线性相关。饱和温度T0越低，表面张力γ越大，所以介稳区越宽。在给定的溶剂中，介稳区主要受热力学项γ的影响，在热力学主导体系中，饱和温度T0的变化对表面张力γ有着显著的影响，说明溶质-溶质和溶剂-溶剂之间的分子键能对温度的敏感性较强。在硫酸钠-水体系中，饱和温度越高，溶质浓度越低，表面张力随着温度的变化呈现直线型变化。因此，调节初始温度是控制硫酸钠溶液介稳区较为有效的方法。

图6 表面张力与饱和温度之间的关系Fig.6 The relationship between surface tension and saturation temperature

通过等式（6）和等式（9）计算了临界尺寸和化学势差，临界尺寸与化学势差之间的关系如图7所示，同一温度下化学势差与临界尺寸成反比，临界尺寸随着化学势差的增加而减小。化学势差随着饱和温度的减小而增加。由等式（9）看出，化学势差随着升温速率的增加而增加，也就是说饱和温度越低、升温速率越快，成核过程中创建固液界面需要更大的驱动力，介稳区越宽，成核就越困难。

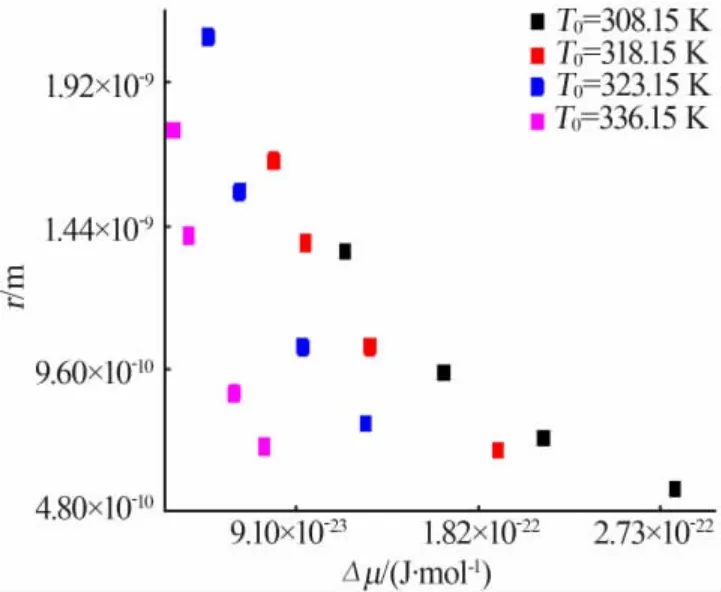
图7 不同饱和温度下临界尺寸与瞬时驱动力之间的关系Fig.7 The relationship between critical size and instantaneous driving force at different saturation temperature

通过等式（5）和等式（9）计算了临界吉布斯自由能和化学势差。从图8可以发现在整个温度范围内临界吉布斯自由能与化学势差是非线性关系，随着化学势差的增加临界吉布斯自由能整体呈现下降趋势；同时，临界吉布斯自由能随着饱和温度的升高而减小，随着饱和温度的升高，加快溶质分子在溶液中聚集，克服自由能势垒所做的功就会减少，介稳区越窄，这与正溶解度体系不同。当饱和温度不变时，升温速率越快（化学势差越大），吉布斯自由能越大，介稳区越宽。

图8 相应升温速率下不同饱和温度下临界吉布斯自由能与化学势之间的关系Fig.8 The relationship between the critical Gibbs free energy and the chemical potential at the corresponding heating rate and different saturation temperature

从等式（5）和等式（6）可以看出，当γ独立于Δμ时，lnΔμ和lnr、lnΔμ和lnΔG服从线性关系。图9显示，在不同饱和温度下，瞬时驱动力与临界晶核尺寸和临界成核势垒均呈负线性相关，瞬时驱动力（化学势差）越大，临界吉布斯自由能和临界晶核尺寸的值越来越小。但是，在不同饱和温度下，lnr与lnΔG是非线性关系，这就意味着γ受Δμ的影响，值得深入去研究γ与Δμ之间的关系，该研究为瞬时驱动力对成核行为的影响奠定了理论基础。

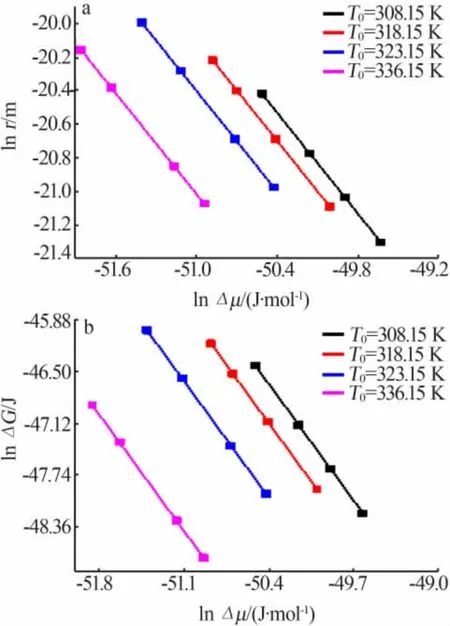
图9 相应升温速率下不同饱和温度下临界尺寸与化学势之间的关系（a）；相应升温速率下不同饱和温度下临界吉布斯自由能与化学势之间的关系（b）Fig.9 The relationship between the critical size and the chemical potential at different saturation temperature and corresponding heating rate（a）；The relationship between the critical Gibbs free energy and the chemical potential at different saturation temperature and corresponding heating rate（b）

图10给出了lnr和lnΔG的关系，可以看出在相同饱和温度下，临界晶核尺寸随临界成核势垒的增大而增大。但是在不同饱和温度下，lnr和lnΔG呈非线性关系，这可能是由于温度对固液界面张力的影响比较显著。

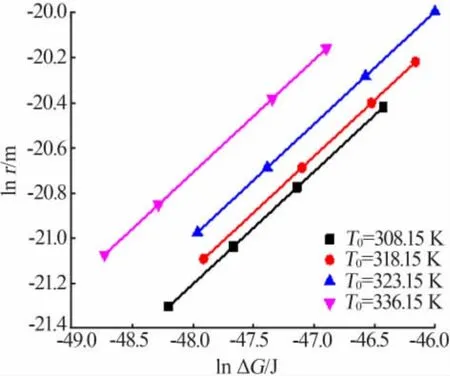
图10 相应升温速率、不同饱和温度下临界吉布斯自由能与临界尺寸的关系Fig.10 The relationship between the critical Gibbs free energy and the critical size at different saturation temperature and corresponding heating rate

根据修正的Sangwal′s模型和经典成核理论，通过等式（10）可以计算得到成核速率。如图11所示，饱和温度越低成核速率越大，更有利于成核过程；当饱和温度保持不变时，随着化学势差的增加即升温速率增大时，成核速率也相应增大。

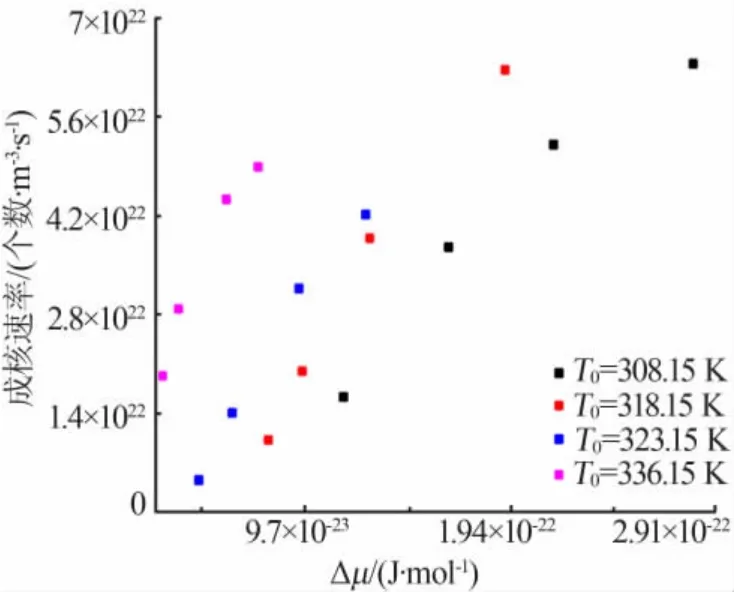
图11 相应升温速率、不同饱和温度下化学势与成核速率之间的关系Fig.11 The relationship between chemical potential and nucleation rate at different saturation temperature and corresponding heating rate

成核速率受结晶推动力和成核温度双重因素的影响。表5为不同饱和温度和不同过热度下化学势。从表5的纵向可以看出，当化学势差随着成核温度的升高而增大（过热逐渐增大）时，结晶推动力成为主导因素，导致硫酸钠成核速率加快。从表5的水平方向可以看出，当化学势差随着（成核温度）饱和温度的减小而增大时，成核温度在与化学势差的竞争中略占优势，因此，即使化学势差减小，成核速率也会增大。也就是说，虽然化学势差是结晶过程的驱动力，但化学势差的降低并不总是意味着成核速率的降低。

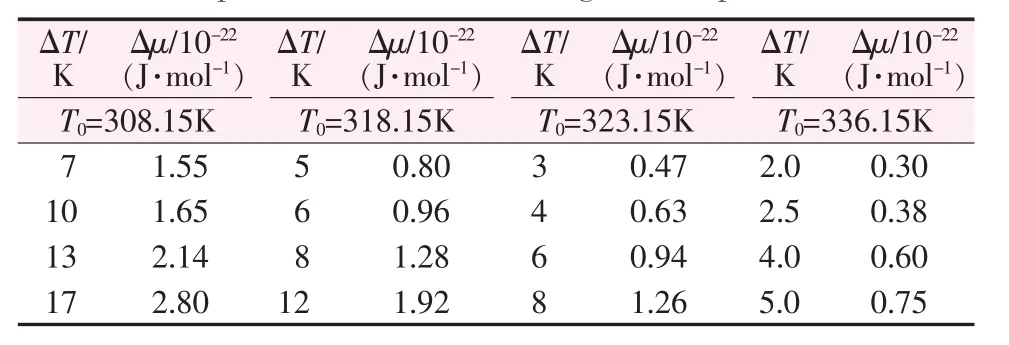
表5 不同饱和温度和不同过热度下化学势的值Table 5 Values of chemical potential at different saturation temperature and different degree of superheat

4 结论

借助FBRM测定硫酸钠在不同饱和温度、不同升温速率下的介稳区宽度，并考察了饱和温度和升温速率对硫酸钠介稳区的影响。结果表明，饱和温度越低、升温速率越快，介稳区越宽、成核越困难。基于修正的Sangwal′s模型计算出体系的固液界面张力、临界晶核尺寸和临界吉布斯自由能。通过Nyvlt′s模型分析了硫酸钠-水体系的成核机理。分析了饱和温度和化学势对成核过程的影响，验证了饱和温度和化学势在成核过程中是竞争关系。数据表明：虽然溶质在固液两相中的化学势差是结晶过程的驱动力，但它并不总会促进成核。以上数据为结晶工艺中的结晶器的设计提供基础数据，并对类似逆溶解度体系提供了有益参考。