采用改进长短时记忆神经网络的水产养殖溶解氧预测模型

曹守启，周礼馨，张 铮

（1.上海海洋大学工程学院，上海 201306；2.上海海洋可再生能源工程技术研究中心，上海 201306）

0 引 言

在水产养殖中，溶解氧（Dissolved Oxygen，DO）已成为预测水质的重要参数[1]。水中溶解氧过高或不足，都会影响生物的繁殖和新陈代谢等生理功能，甚至严重影响生物的正常生长[2-3]。然而，溶解氧易受天气、水质、人类活动等多种因素的影响[4]，具有非线性、大惯性、强耦合、时变性等特点[5-7]。因此，加强溶解氧预测模型研究[8]，提高水产养殖减灾防灾能力，保障水产养殖的安全，已成为农业生产的关键内容[9]。

预测水质变化是一项艰巨的任务，涉及多参数动态时延过程，很难用简单的数学公式或传递函数来体现其模型。此外，传感器的准确度会受到环境因素的影响而降低，导致数据丢失或产生不确定的异常值，这对预测精度提出了挑战。

在现有的解决上述 2个问题的方法中，支持向量机（Support Vector Machine，SVM）和人工神经网络（Artificial Neural Network，ANN）是2种广泛应用于水质预测的方法[10]。为了提高预测精度，Yu等[11]提出了一种基于径向基函数神经网络（Radial Basis Function Neural Network，RBFNN）数据融合方法和最小二乘支持向量机的混合溶解氧预测模型。但是支持向量机容易出现对数据丢失敏感、训练耗时、预测性能差等问题，很难为各种应用选择合适的核函数[12]。相较于支持向量机模型，ANN可以容忍一定程度的数据缺失[13]。Faruk等[10]提出了季节性的平均自回归模型（Autoregressive Integrated Moving Average Model，ARIMA）和神经网络反向传播模型相结合的水质参数月度预测方法。然而，由于网络拓扑和数据的复杂性，人工神经网络模型往往存在过拟合、稳定性差和耗时等问题。上述提及的预测方法均属于浅层结构的机器学习方法，在处理大规模数据时鲁棒性较差，导致模型缺乏长效性和扩展能力，不能完全反应数据的本质特征[14]。

近年来，很多基于深度学习的方法在不同的领域得到广泛应用。深度学习方法能够实现高维函数的逼近，挖掘数据的隐含信息，与浅层结构的机器学习方法相比具有更强的数据学习能力和泛化能力，能高度抽象化数据特征[15]。在现有的方法中，神经网络模型是解决复杂预测问题的强有力工具。循环神经网络（Recurrent Neural Network，RNN）是一种以序列数据为输入的递归神经网络算法[16]，被广泛应用于序列的非线性特征学习，如语音识别和时间序列预测等[17]。长短时记忆神经网络作为RNN神经网络最受欢迎的变体，可以有效地解决 RNN训练时存在的梯度弥散和梯度爆炸问题[18]。Huan等[19]采用梯度提升决策树对数据进行特征选取，建立长短时记忆神经网络溶解氧预测模型，并与 PSO-LSSVM 模型（Particle Swarm Optimization Least Squares Support VectorMachine）对比，证明了其模型的优越性。Fu等[20]应用LSTM神经网络预测交通流。Garn等[21]使用长短时记忆（Long Short-term Memory ，LSTM）神经网络预测英国租户的财务状况，并及时干预可能拖欠租金的租户，以避免收入损失。目前，LSTM神经网络已广泛应用于不同场景的预测，并从很大程度上提高了预测的准确性。LSTM神经网络能够有效预测集约化养殖中DO含量，可以平衡预测的稳定性和准确性。

因此，本文提出了IPSO-KLSTM（Improved Particle Swarm Optimization Long Short-term Memory Neural Network Model Based on K-means Algorithm）模型预测水产养殖溶解氧，应用 K-means算法对数据进行聚类，并利用改进的PSO算法对LSTM网络进行参数选取，以期提高预测精度，并验证模型的准确性和可靠性。

1 数据和方法

1.1 试验区域

试验选取上海市崇明光明田原清水蟹养殖示范基地为试验区域。该养殖区域水资源极其丰富，水中石油类、重金属等水化因子符合渔业水质标准要求，区域面积约78.5 hm2，养殖水深为1.8 m，溶解氧、pH传感器均置于水下1.0 m处，所有数据都已传输到无线传感器监控系统。

1.2 数据来源

水产养殖环境数据采集来自上海海洋大学开发的远程低功耗无线监控系统，如图1所示。该系统集成水质和气象传感器，并通过NB-IoT技术传输数据到远程终端，终端应用软件对数据进行预测预警处理。试验采用的传感器记录了从2021年5月1日—7月6日共67d的溶解氧、pH值、温度、湿度、气压、光照、风速、风向等养殖环境数据，采集间隔为15 min，每天可获取96条数据，共收集了6 432条数据记录，用于2021年7月7、8日的溶解氧预测。在 67d的样本中，训练集与测试集占比为7∶3。将历史数据的 7个影响因子和溶解氧值作为预测模型的输入向量，模型的输出结果为预测日的溶解氧值。

2 预测模型构建

2.1 确定影响DO的环境因素权重

由于采集到的原始数据具有不同维度和量纲，容易影响模型的最终预测效果[22]。在模型研究前，首先对数据进行公式（1）的归一化处理。

式中xk和分别为原始数据和归一化后的数据，xmin和xmax分别为原始数据的最小值和最大值。

水产养殖在线监测系统采集了大量不同类型的数据，若将所有数据直接作为模型的输入，模型会变得非常复杂。本文采用皮尔森相关系数公式（2）选取DO的关键影响因子，以减少输入维度并解决信息冗余问题。溶解氧与不同环境因素之间的皮尔森相关系数结果如表1所示。

式中x和y为维度为1×m的向量，xi和yi分别为向量x和y的第i个元素，和分别为向量x和y元素的平均值。

从表1中可以看出，每个因素的特征重要性排序为光照强度、温度、气压、湿度、pH值、风速和风向。本文选取前6个环境因素作为溶解氧预测模型的输入样本，以降低数据维度和复杂度。

表1 溶解氧与各影响因子的皮尔森相关系数Table 1 Pearson correlation coefficient among dissolved oxygen and influencing factors

2.2 相似度K-means聚类

为避免无规则样本直接作为输入导致预测精度低、收敛慢等问题，本文在预测前先采用 K-means算法将环境因子进行聚类，找出变量的相似性变化规律，然后在同簇别中建立LSTM神经网络模型进行溶解氧预测。

2.2.1 相似度统计量权重确定

环境因子的权重随天气变化会有一定的差异，在计算相似度统计量时，统一各影响因子间的权重会导致相似度大的因子直接决定总体相似度，造成误差[23]。因此，采用灰色关联系数法计算环境因子对平均溶解氧的权重。根据历史天气记录，将收集到的数据按照不同的温度和光照强度分为晴天、多云、阴天、雨天和混合天气（一天中出现2种不同天气类型）5类，气象数据划分见表2，分别计算5种天气类型的因子权重。

表2 天气类型气象数据划分Table 2 Division of meteorological data for weather types

假设有e天某天气类型的历史数据，将每天的平均酸碱度pHavg，日平均温度Tavg，日平均湿度Havg，日平均气压Pavg，日平均风速Savg和日平均光照Lavg作为反映该天的影响因子。构造 6个大小为d×1的属性因子向量z1～z6。以日平均溶解氧作为参考向量，构造出e×1的溶解氧向量z7，利用灰色关联系数法求出 6个因子向量与溶解氧向量在第e个分量的关联系数。

式中λj(a)为因子向量与降解氧向量的关联系数；ρ是[0,1]之间的分辨系数，ρ通常取0.5，a为天气类型的天数；得到的不同类别中环境相关因素对溶解氧的影响权重见表3。

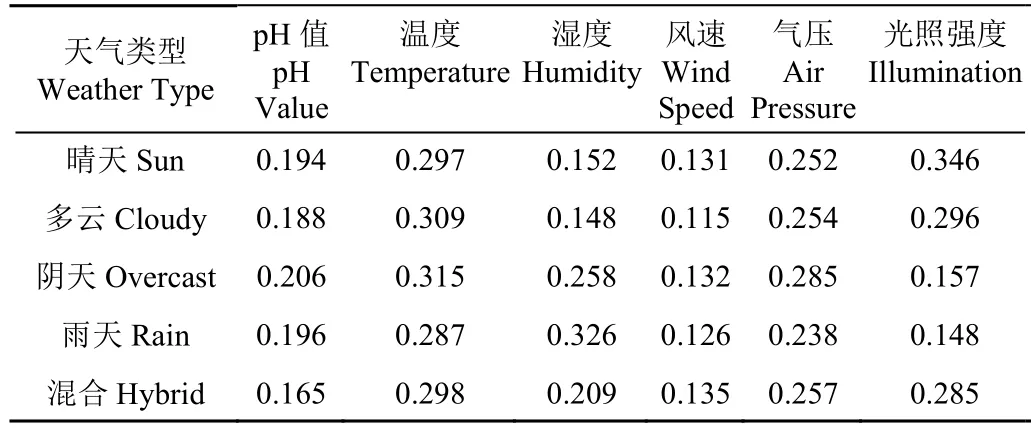
表3 不同天气类型下的影响因子权重Table 3 Weight of influence factors under different weather types

式中rj是zj和z7之间的关联度，jσ为各因子的权重。

2.2.2 组合聚类相似度统计量

在聚类分析中，常用欧氏距离和角余弦来度量 2个样本之间的相似度。假设要比较的 2个个体分别是溶解氧X和其他任意一个影响因子Y。它们都包含t维特征，即X= （x1,x2,… ,xt），Y= （y1,y2,… ,yt）。

欧式距离用来度量多维空间中点之间的绝对距离，反映样本的数值差异。公式如下

角余弦使用向量空间中 2个向量之间的角的余弦值作为2个个体之间差异的度量。公式如下

由于溶解氧在不同环境条件下的变化趋势复杂，仅用1个距离指标来计算样本间的相似性有一定的局限性。为综合考虑历史数据中的数值信息和形状信息，结合欧氏距离和角余弦计算方法，采用宦娟等[9]提出的改进的相似统计量。又由于统一各影响因子间的权重会导致相似度大的因子直接决定总体相似度，造成误差，故将上述计算的不同环境因子对溶解氧的影响权重jσ嵌入到该方法中，以计算样本间的趋势相似性。计算公式如下

其中，

式中xij和yij为样本x和y在第i时刻的第j个特征，其值介于0到1之间。α和β分别是夹角余弦Dcosxy和欧氏距离dxy之间的权重系数，m为特征因素，t为监测时刻。这 2个值将随天气条件而变化，天气变化剧烈时α接近于1，否则，β接近于1，且α+β=1，σj是公式（5）中第j个环境因子对溶解氧的影响权重。

2.2.3 基于组合相似度的K-means聚类

历史天气记录简单将天气分为晴天、多云、阴天和雨天，划分不够明确。易出现不同天气情况溶解氧趋势相似及一天中出现不同天气类型难以归类的情况。又K-means算法的初始聚类中心是随机选择的，这会增加整个计算的迭代时长。因此，本文基于天气类型不同对数据进行有效聚类。在对晴天、多云、阴天、雨天、以及混合天气类型的分类中初始化聚类中心，以节省运算时间和避免出现局部极值。

基于给定的聚类目标函数采用K-means迭代更新算法。每个迭代过程都往目标函数缩减的方向上进行[24]。最终的聚类结果使目标函数得到最小值，从而达到较好的分类效果。聚类结果如图2所示，类1～5分别为改进K-means聚类算法对原始数据的不同分类。从图中可以看出，每个簇中的数据对象都是集中的，簇与簇之间的分散程度相对较高。

2.3 长短时记忆神经网络

长短时记忆（Long Short-term Memory，LSTM）神经网络是一种特殊的循环神经网络（Recurrent Neural Network，RNN）[25]，解决了RNN存在的梯度弥散和梯度爆炸问题，被广泛应用于时间序列中具有长时间间隔和时滞的预测场景。

LSTM在标准RNN的基础上增加了更多的神经网络层，增加了记忆单元和输入门、输出门、遗忘门 3个具有记忆功能的模块，有选择地让信息通过，每个门的功能各不相同。

遗忘门负责决定从记忆单元中丢弃哪些信息。更新公式如下

式中wfx、wfh、wfc和bf分别表示遗忘门的权重系数和偏置。

输入门负责决定哪些信息可以保存在记忆单元中。更新公式如下

式中wix、wih、wic和bi分别表示输入门的权重系数和偏置。wcx、wch、bo分别表示候选向量的权重系数和偏置。

输出门决定将输出哪些信息。除所需的信息外，没有其他信息可以通过输出门。其表达方式如下

式中it、ft和ot分别为输入门、遗忘门和输出门，xt为t时刻的输入，σ(·)为 sigmoid激活函数，tanh(·)为双曲正切激活函数，wox、woh、woc分别表示输出门的权重系数，Ct和为t时刻的候选向量和候选向量更新值，ht和ht-1分别为t、t-1时刻的输出。

2.4 改进PSO优化的聚类LSTM神经网络

2.4.1 粒子群优化算法

粒子群优化（Particle Swarm Optimization，PSO）算法最早由 Eberhart等[26]提出，通过群体中个体之间的协作和信息的共享，使整个群体的运动在问题求解空间中由无序演化为有序，从而获得最优解[27]。

d维搜索空间中，存在n个粒子Y= (Y1, … ,Yn)，其中Yi= (yi1,yi2,… ,yid)T表示优化问题的潜在最优解和粒子在解空间中的位置。粒子的速度V= (V1, … ,VN)包含了它的距离和方向，其中Vi= (vi1,… ,vid)T。粒子特性由 3个指标表示：“位置”()、“速度”()和适应度值。在每次迭代中，粒子通过个体极值和群体极值更新其速度和位置。更新公式如下

式中k为当前迭代次数，ω表示惯性权重，c1和c2表示学习因子，r1和r2为随机设置的常数，取值范围[0,1]。Pi=(pi1,… ,pin)T和Pg= (pg1,… ,pgn)T分别代表个体最佳位置和群体最佳位置。速度的范围是 [vmin,vmax]。

2.4.2 改进粒子群优化算法

PSO作为一种元启发式优化算法，可以用来优化LSTM的参数选择，以减少计算时间，提高预测精度。粒子群算法在解决复杂优化问题上有着显著的效果，但在处理优化问题时缺乏有效的参数控制。易出现收敛速度慢、易陷入局部最优、后期迭代精度低等问题。

1）改进的惯性权重

根据之前的相关研究[28]，惯性权重是PSO模型中最重要的可调参数之一，适当的惯性权重值能平衡算法的局部和全局搜索能力，从而减少了定位最优解所需的迭代次数，并提高了PSO的性能。经典的时变惯性权重方法虽然易于实现，但由于不同的问题有其自身的特点，因而不能体现显著的优势。由于惯性权重与迭代时间呈负相关，粒子在进化初期具有较大的惯性权重以促进群体的多样性。随着迭代次数的增加，惯性权重呈非线性减小。惯性权重的减小可以显著地增强粒子的收敛性。因此本文采用非线性双曲正切函数来平衡局部和全局搜索。表达如下

式中Tω为改进的惯性权重，ωmin是最小惯性权重，ωmax是最大惯性权重。T是当前迭代，Tmax是最大迭代次数。现用Tω代替式（17）中的ω。每个粒子惯性权重Tω根据上式独立更新。

2）改进的学习因子

学习因子c1和c2主要用于调整粒子移动到个体最优位置和全局最优位置的步长。在实际应用中，随着迭代过程的推进，通常要求c1值由大变小，以加快迭代初期的搜索速度，提高全局搜索能力。同时要求c2值由小变大，以便于在迭代后期进行局部细化搜索，同时提高精度[29]。然而，标准PSO通常将其设置为122c=c= 不能满足实际应用的要求。因此，引入余弦函数来改进学习因子，如下式所示

2.4.3 IPSO-KLSTM网络预测模型

溶解氧时间序列数据受到多方面因素的影响，具有复杂的不稳定性、非线性和时变性。为了准确地预测溶氧变化趋势，本文以在时间序列分析中实现性能优越的LSTM模型为基础，在预测前进行K-means聚类，同时提出改进的 PSO算法来优化模型参数，建立IPSO-KLSTM溶解氧预测模型。其预测流程如图3，具体实施步骤如下：

1）通过远程无线监测系统获取试验区域的水质、气象数据，并对其进行预处理，利用皮尔森相关系数筛选出溶解氧的关键影响因子，以降低模型输入的维度和复杂度；

2）为避免天气状况相近而溶解氧变化差异较大的情况，采用灰色关联度计算不同天气下影响因子相似度，根据溶解氧的浓度和曲线形状，利用 K-means算法对数据进行聚类，图3中在建立LSTM网络前数据被分为1～5类，找出数据之间的相似性，以提高预测的准确度；

3）设定 IPSO参数并初始化粒子：确定种群大小、粒子维数、迭代次数、学习因子、惯性权重以及待优化参数的定义区间。初始化粒子的位置和速度，随机产生粒子Yi,1(node,look_back)，其中node表示隐含层神经元的个数，look_back表示时间步长；

4）设置粒子的适应度函数：适应度函数用来衡量每个粒子的性能。以当前粒子作为每个粒子的个体极值点，以适应度最小的粒子作为全局极值点。在 LSTM的训练和测试过程中，目标是使测试样本的实际值和预测值之间的误差最小化。因此，IPSO的适应度函数定义为

式中M为验证样本数，yij和分别为验证样本的真实值和预测值；

5）更新粒子的速度和位置：计算每个粒子的适应度值，确定个体最优适应度值和群体最优适应度值；

6）完成预测并对结果进行分析：将IPSO算法在满足最终条件时得到的参数值代入LSTM神经网络模型，建立IPSO-KLSTM水产养殖溶解氧预测模型，然后将测试样本输入模型进行预测，最后对预测结果进行分析。

3 结果与分析

3.1 算法参数设置

所有试验均在MATLAB环境下进行，并在2.4GHz内核处理器、8.0G内存和Microsoft Windows 10的PC机上运行。在本试验中，使用2.2节提出的聚类模型将所有数据（6432个数据集）划分为5个簇。分别在各个类中应用IPSO-KLSTM模型。利用IPSO算法得到了溶解氧预测模型的最优参数node和look_back。IPSO的初始化参数如下：群体大小P=50，惯性权重ωmax= 0.95，ωmin= 0.3，迭代次数T=200，归一化样本的适应度精度为0.005。IPSO参数的选择是基于大量的试验和参考[30]，这些值在训练数据集上提供了最小的MSE和最好的计算效率。这表明IPSO算法收敛速度快，更适合于寻找LSTM模型的未知参数。通过IPSO算法得到最优组合参数，即node=10，look_back=20。

3.2 模型性能评估

为了进一步检验模型的预测性能，采用平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）、均方根误差（Root Mean Square Error，RMSE）[31]、平均绝对误差（Mean Absolute Error，MAE）和纳什系数（Nash-sutcliffe Coefficient，NSC）[32]对预测结果进行了评价。这些度量可以从不同的数学角度反映原始数据与预测数据之间的误差和拟合程度。这些指标分别由公式（23）～（26）计算。

式中N为每个数据集中预测时间点的数量，Yi是原始数据，fi为预测值，表示原始数据的均值，当NSC的值越高，且MAPE、RMSE和MAE值越低时，模型越精确。

3.3 模型的对比分析

为了验证提出模型的预测性能，本文采用不同的预测模型进行比较。比较模型有粒子群优化的 K-means长短时神经网络模型（PSO-KLSTM）、PSO优化最小二乘支持向量机模型（PSO-LSSVM）、PSO和LSTM组合模型（PSO-LSTM）和传统的极限学习机模型（ELM）、反向传播（BP）神经网络模型、长短时记忆（LSTM）网络模型。为了验证模型在不同天气状况下的预测性能，分别选取2021年7月7、8日作为预测日，预测其24h内的溶解氧含量，如图4所示。其中7月7日是晴天，最低、最高温度分别为 26、35℃；平均光照强度为38 643 Lux。图4 a显示了其6种不同模型对溶解氧含量预测曲线，随着光照强度的增大，引起水中植物的光合作用转换增强，氧气逐步积累在下午四点后达到峰值。同时图5展示了这一天中不同模型对应的预测误差，从图中可以看出，本文提出的IPSO-KLSTM较其他5种模型的误差曲线波动较小。这是由于溶解氧受到光照强度、温度、气压等多种环境因素的影响，在预测前对数据集进行环境因子分析聚类，可以优化输入样本，避免差异样本的干扰，有效提取溶解氧的变化特性。另外，利用IPSO方法优化LSTM模型所需的参数选取，可以提高模型搜索速度，克服了传统LSTM模型在参数选择上的盲目性和局限性，从而提高模型预测精度。

7月 8日为混合天气类型，最低、最高温度分别为25、31 ℃；平均光照强度为31 047 Lux，其白天大部分时间较为晴朗，至下午16:30突降暴雨。图4 b显示了该天气状况下 6种模型的预测曲线，天气突变使得光照强度降低，水生物光和作用受到影响，同时气压降低导致水体对氧的溶解度降低，溶解氧含量快速下降，图5中显示其误差曲线变化波动较大。

表4为不同模型对应的性能评估，可以看出当天气发生突变时，本文提出模型的MAPE、RMSE、MAE和NSC分别为0.129 5、0.645 3、0.461 3和0.902 2。与未经过相似度聚类的模型相比，IPSO-KLSTM预测效果较好，该模型能构造最优化的样本训练集，能够根据天气变化做出相应的学习训练，快速获取最新样本，对突变的天气状况样本具有较强的学习能力，同时也获得了更好的泛化性能，从而降低天气突变时的预测误差。与传统的LSTM、ELM和BP模型相比，该算法的RMSE分别提高了17.10%、24.89%和24.21%，说明只依靠网络自身训练的模型，其预测效果不能满足实际的环境需求，改进的LSTM较好的平衡了预测的稳定性和准确性，能够容忍因不确定的混合天气类型而导致的传感器数据异常或缺失，是一种适合用于预测集约化养殖DO含量的有效方法。

表4 2021年7月7-8日模型预测结果分析Table 4 Analysis of model forecast results on July 7 and 8, 2021

通过对 2种天气情况的预测分析，可以看出，在天气突变的情况下，IPSO-KLSTM 预测误差略有增加，但优于其他5种模型。能有效预测水产养殖中溶解氧含量，为水产养殖的预测和预警提供帮助。

4 结 论

为了解决溶解氧含量预测中传统预测方法预测精度低、鲁棒性差的问题，将 K-means聚类和长短时记忆神经网络（LSTM）相结合，同时引入改进粒子群优化算法（IPSO），建立了池塘养殖河蟹养殖中溶解氧含量的非线性预测模型，得出以下结论：

1）本文利用灰色关联系数确定在不同天气类型下影响因子对溶解氧的权重，并结合改进相似度统计量，用K-means算法将原始数据集划分为5个不同的簇，通过选择与预测日溶解氧高度相关的类别作为输入数据，有利于选取优质训练样本，避免了因天气差异造成的不同趋势样本间的干扰。

2）通过改进 PSO的惯性权重和学习因子，优化LSTM的参数选取，其最优参数组合为隐含层神经元个数node=10，时间步长look_back=20。能避免参数设定的盲目性，减少人工选择参数的主观影响。

3）针对不同天气状况，将提出的模型与PSO-LSSVM、PSO-LSTM和传统单一的BP、ELM、LSTM预测模型相比，本文建立的模型其预测结果更接近真实值。在良好天气情况下，其预测误差曲线波动较小。当天气发生突变时模型具有较低的RMSE、MAE、MAPE和更高的NSC，分别为0.129 5、0.645 3、0.461 3和0.902 2。拟合效果比较理想，一定程度改善了突变状况下的数据缺失、鲁棒性差等问题，在大规模集约化养殖中具有一定优势。

在未来的工作中，我们将在其他类型的水产养殖参数的应用领域进行试验和探讨，并加以推广。同时，我们会更加注重不同模型的对比，以便对模型的性能进行更深入的分析和探讨。