基于犹豫模糊TOPSIS的绿色矿山多属性评价方法

2021-10-12罗德江吴昊何苏李俊波浦华王月奇

矿产综合利用 2021年4期

罗德江，吴昊，何苏，李俊波，浦华，王月奇

（1.成都理工大学数学地质四川省重点实验室，四川成都 610059；2.成都理工大学数理学院，四川成都 610059；3.成都理工大学管理科学学院，四川成都 610059）

我国绿色矿山建设开展以来，取得了可喜的成绩，但国家级绿色矿山试点单位占比偏低[3]。为了全面推进绿色矿山建设进程，2018年1月完成了绿色矿山建设规范（报批稿），2018年10月矿业九大行业《国家绿色矿山建设规划》已由自然资源部发布正式实行。绿色矿山建设规范主要从矿区环境、资源开发方式、资源综合利用等六个方面做出了相应要求。在这些具体的要求中，既有定量的指标，其指标值为精确值，如矿区绿化率、废物处置率等，也有定性指标，其指标值为语言变量，如管理规范、企业核心价值观、办矿理念等。在我国不断加强绿色矿山建设实践的过程中，部分企业取得了很好的效果[1-6]，但如何对企业的绿色矿山建设成效进行科学评估，以最大程度激发企业积极性，促使绿色矿山建设可持续和长效化，是今后的重要工作之一。

1 概述

目前，许多学者依据不同的理论，从不同的视角出发，研究了绿色矿山的评价体系及其评价方法。

评价指标体系设计是否科学合理，对绿色矿山建设评价结果的客观性与准确性会产生直接的影响[7]。宋学峰等根据《国家绿色矿山基本条件》从管理、企业文化和技术等三个方面，构建了包括依法办矿、规范管理、社区和谐与企业文化、综合利用、技术创新、节能减排、环境保护和土地复垦等8个指标的评价体系[8]；汪文生等针对能源矿产中的煤炭这一矿种，选取了研发投入、安全生产累计投入、节能减排投入作为模型的投入指标，以煤炭生产能力、百万吨死亡率和绿化覆盖率作为产出指标，对8家煤炭企业绿色矿山建设效率开展了评价[9]；靖培星等从基本条件、规范管理、资源利用、节能减排、技术创新、环境保护、土地复垦、企业文化与社区和谐等6个方面出发，构建了包含40个指标的评价体系，将绿色矿山建设水平分为“高”、“较高”、“中”和“低”4个等级[10]；宋海彬等[11]针对煤炭企业，从财务、客户、内部业务流程和创新能力等4个方面，选取了25个指标，形成了一个较全面和科学的反映企业可持续发展能力的指标体系；闫志刚等[12]通过对矿山建设中的污染源分析，从矿山生产、节能与环保和管理与安全等3个方面，构建了一个三级指标体系，将绿色矿山建设分为“优秀”、“良好”和“合格”等级；张文龙等[13]认为绿色矿山评价指标的构建应考虑资源开发与利用的全过程，从资源勘探、矿山建设、矿山生产、矿山闭坑到恢复土地使用功能等不同的阶段，选取能反映绿色矿山建设水平的一系列指标，并给出了指标量化与权重计算的建议；黄敬军等[14]构建了盐矿绿色矿山评价指标；张敬明等[15]提出了构建绿色矿山评价指标的原则和框架，并从社会经济、矿产资源开发利用效益、科技资源投入和环境效益等4个方面构建了评价指标体系。从已有的研究成果分析，构建的评价指标因评价对象和评价出发点不同，构建的指标也不尽相同，但一般都考虑了矿产资源开发利用、科技创新和矿山环境等方面；其次是指标值的提取，针对评价指标中的定性指标大多采用专家评分法获得，具有一定的主观性。

绿色矿山评价方法涉及到多属性，综合评价方法得到了广泛的认可与应用[16]。汪文生等从投入与产出的角度，采用数据包络分析法（DEA）对煤炭企业绿色矿山建设资源进行了评价；靖培星等针对指标值为直觉模糊集的形式，提出模糊熵和变权理论确定评价指标的权重，采用灰色聚类模型对井工煤矿绿色矿山建设进行评价，为绿色矿山评价引入了新的方法；黄敬军等针对指标中既有定量指标也有定性指标这一特点，运用层次分析法确定各指标的权重，采用多级模糊模式识别模型开展盐矿绿色矿山建设评价，并根据评价结果分为优、良、中、差4个级别；宋学峰等通过模糊数学综合评价方法对湖南新田钨矿绿色矿山建设水平进行了评价。绿色矿山评价是一个复杂的系统，涉及到资源条件、技术、环境和管理等多种类型的变量，由于部分指标具有模糊特征，评价者往往不能给出各指标值的精确数；其次，当评价者确定某一指标属于一个集合的隶属度时，往往是犹豫或不确定的。如对某一绿色矿山建设水平的指标“企业管理”，一部分评价者给出0.8，另一部分给出0.9，且不能彼此说服。以上两方面的原因造成了不同的评价者对同一绿色矿山建设水平的评价结果不一致，且很难对不同的评价结果做出取舍。将犹豫模糊集理论引入到绿色矿山建设水平评价中，该指标“企业管理”可表示为一个犹豫模糊数{0.8，0.9}或{0.9，0.8}。表明该指标的隶属度不是0.8或0.9，也不是在区间0.8到0.9内变动，而是表明该指标两种可能的值。针对绿色矿山评价这种实际情况，本文将犹豫模糊多属性决策方法引入到绿色矿山建设水平的评价中，并对中国攀西地区的钒钛磁铁矿绿色矿山建设水平开展评价。

2 指标评价

2.1 评价指标体系

绿色矿山指标体系构建是开展绿色矿山建设评价的主要工作之一。本文以自然资源部出台的相关文件、规划和规范为基础，综合国内学者的工作成果，从技术经济、企业管理和矿山环境等三个方面构建评价指标体系。

(1)矿区环境

要求矿区开发规划和功能分区合理，全面实现矿区绿化，生产过程中产生的废弃物全部进行处置，矿山生产和运输等各环节管理规范有序。

(2)资源开发方式

矿山应根据自身的资源赋存状况和生态环境特征，因地制宜选择采矿和选矿工艺；要积极开展技术创新，改进技术工艺；企业的资源开发利用方式应与区域内的环境保护、资源保护以及城乡建设相协调；应最大限度的减少对自然环境的破坏，对已破坏的环境应及时治理恢复。

(3)资源综合利用

矿山应不断的提高资源综合利用水平，保护不可再生的矿产资源。要加强共伴生资源的勘查与开发利用，在现有技术经济条件下可利用的应全部利用；科学利用矿山的固体废弃物和废水等，提高企业效益，保护环境，发展循环经济。

(4)节能减排

矿山应采用新技术、新工艺、新设备和新材料，控制并减少单位产品能耗，减少固体废弃物、废水和废气等“三废”的排放。

(5)科技创新与数字化矿山

企业作为创新的主体，应建立科技研发队伍，对企业生产中的关键技术开展技术攻关，不断改进企业的工艺技术与设备水平；采用计算机和智能控制等技术建设智能矿山和生产自动化系统，提高矿山生产的自动化水平，实现生产全过程集中管控和信息联动。

(6)企业管理与企业形象

矿山应建立完善的资源管理、生态环境保护、安全生产等规章制度与工作机制；具有以人为本、创新学习、绿色发展的企业核心价值观，具有符合企业特点和推进实现企业发展战略目标的企业文化；构建矿山与地方共建、利益共享和共同发展的理念，提高矿区人民生活质量。

2.2 评价方法

在复杂系统的评价中，因涉及到管理、技术、环境和资源等各种类型的属性，往往存在着模糊不确定性。如何解决复杂系统评价或决策的不确定性，一直是一个广泛关注的焦点。扎德[17]于1965年提出的模糊集理论是解决此类评价问题的一类有效方法。自模糊集理念提出以来，相继出现了直觉模糊集、区间型模糊集和犹豫模糊集等许多拓展形式。目前在众多学者的关注与研究之下，犹豫模糊集相关理论得到了不断的完善，且深入到各个学科，应用于决策分析和聚类分析等领域。

在众多的多属性决策方法中，TOPSIS是一种应用广泛的多属性决策方法。TOPSIS的基本思想是通过计算待评价方案与理想方案之间的距离来进行方案排序，以确定最佳方案。在这一方法中，属性值为精确值，而大量的决策问题属性值存在语言变量与区间值的情形。解决这一矛盾有效方法是模糊集及其拓展形式，并产生了模糊TOPSIS、犹豫模糊TOPSIS。本文提出将犹豫模糊TOPSIS应用于绿色矿山建设水平评价，并进行实证分析。

考虑一个多属性决策问题：A={A1， A2…，Am}为方案集，Ai为待评价的矿山，为指标集。X={X1，X2…，Xn}第i个待评价矿山Ai关于X的一个犹豫模糊集为：

其中表示第i个矿山Ai在第j个属性xi下可能的隶属度，该隶属度可由一个犹豫模糊元素hij来表示，则犹豫模糊决策矩阵H可表示为：

2.2.1 权值的确定

评价指标权重的估计在多属性决策中扮演了重要的角色。在绿色矿山综合评价中，指标权值对评价结果有着重要的影响，因此合理确定各指标权值是绿色矿山评价的关键问题之一。主观赋权法充分利用了专家知识，较好的体现了决策者的意向，但评价结果具有较大的主观性；客观赋权法则较好的克服了主观性，具有较强的数学理论依据，但没有利用专家的知识。针对由数值信息表示的多属性决策问题，最大偏差法对具有较大偏差的指标赋予较大的权重，对具有较小偏差的指标赋予较小的权重[18]。在犹豫模糊环境下，各评价指标的权重可归结为一个优化问题：

式中：Wj为评价指标的权重，dij为犹豫模糊元素之间的距离。dij采用模糊欧氏距离：

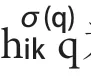
2.2.2 犹豫模糊理想点的确定

TOPSIS是通过计算待评价方案与理想方案之间的接近程度来确定最佳方案，使用方便灵活，应用比较广泛。在该方法中，确定正理想解与负理想解是关键之一。在犹豫模糊环境下，可拓展到犹豫正理想解S+与犹豫负理想解S-[32]。

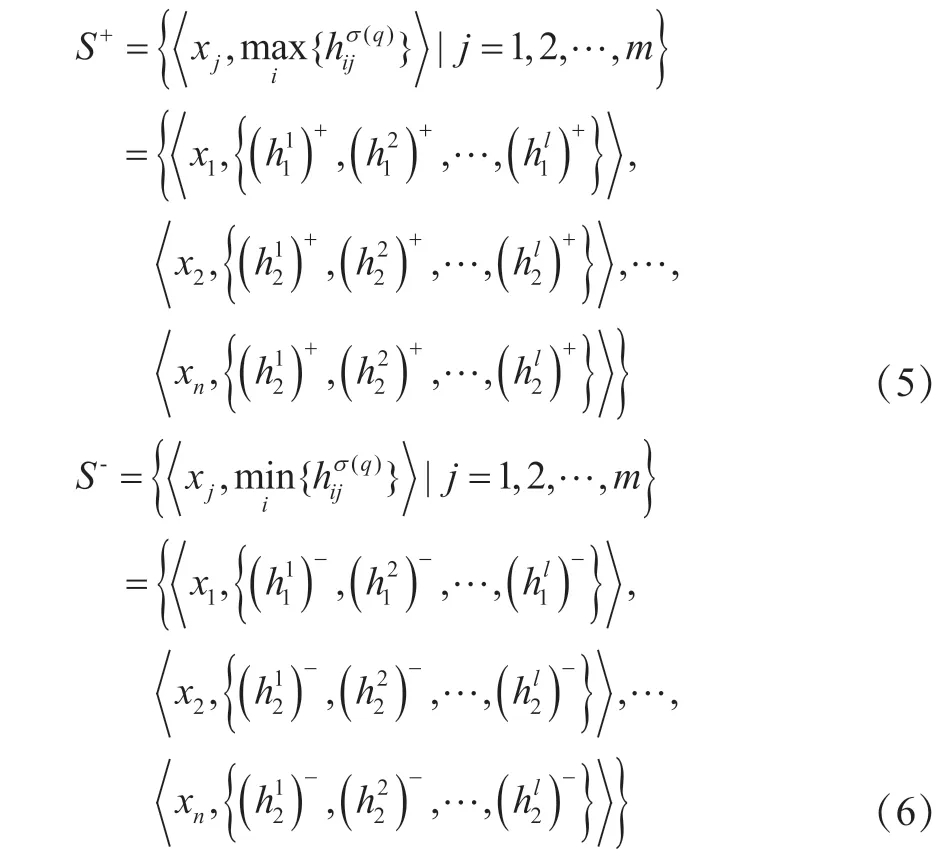
式中： xi为i第个指标。

2.2.3 基于犹豫模糊的TOPSIS评价方法

在确定完评价指标的权重和犹豫模糊正理想解和犹豫模糊负理想解后，把TOPSIS决策方法扩展到犹豫模糊集中，对各待评矿山排序，对各绿色矿山建设水平进行评估。

（1）根据评价指标集，获取指标值；根据乐观原则或悲观原则，通过拓展犹豫模糊元素进行标准化处理。

（2）计算各评价指标的权重。在绿色矿山评价中，矿区环境、资源开发方式、资源综合利用、节能减排、创新与数字化矿山、企业管理与企业形象等指标的重要性是不同的，通过求解较优化模型（2）来确定各指标的权重。

（3）根据式(4)与式(5)确定犹豫模糊正理想解和犹豫模糊负理想解。

（4）计算各矿山到犹豫正理想解与犹豫负理想解的加权距离。各方案间的距离由Hamming距离、Euclidean距离和、Hausdorff距离等在犹豫模糊环境下的拓展得到[19],包括犹豫模糊Hamming距离(HNHD)、犹豫模糊Euclidean距离(HNED)、犹豫模糊Hamming-hausdorff距离(HNHH)和混合犹豫模糊Euclidean距离(HHNED)。

（5）计算各方案的相对贴近度。各方案的相对贴近度（Ci）的计算公式为：

式中：di-为各矿山到犹豫负理想解的加权距离；di+为各矿山到犹豫正理想解的加权距离。

（6）对各绿色矿山建设水平进行评估。根据步骤（5）中计算的相对贴近度，按照Ci的值对方案进行排序，Ci值越小，对应的绿色矿山建设水平越高。

3 研究区和数据来源

3.1 研究区

攀西地区位于中国的西南部，包括攀枝花市和凉山彝族自治州。攀西地区地处横断山系,属青藏高原、云贵高原向四川盆地的过渡带。攀西地区曾发生过多次泛大陆解体、离移、拼接和镶嵌以及多期多阶段构造-岩浆-流体活动及变质变形作用，地质构造复杂多样，多旋回岩浆活动强烈，为区内矿产资源形成和聚集提供了有利条件。

攀西地区是我国钒钛磁铁矿矿床高度集中分布的成矿带，该成矿带南北长约 300 km，东西宽10 ～ 30 km，面积约 6 000 km2，是世界上同类矿床的重要产区之一。攀西地区的攀枝花矿区、红格矿区、白马矿区和太和矿区等4 个矿区构成了特大型矿床，矿体厚度达数十米至200 m 以上，伸数百米至千余米。攀西地区钒钛磁铁矿探明储量 93.96 亿t，其中钒的储量以V2O5计为 2348 万t，钛资源量为8.7 亿 t，约占全国各类铁矿资源的 1/5，是国内著名的三大综合利用矿产资源之一。

攀西作为我国钒钛磁铁矿资源最丰富、最集中的地区，其钒钛磁铁矿资源开发与综合利用已取得了显著成就，特别是最近几年，开发势头强劲，进入了快速发展阶段，矿山 “三率”和矿产资源综合利用水平都得到了显著的提高，已成为我国钒钛产业发展较好，钒钛资源开发利用水平较高、开发前景最广阔的地区。

3.2 数据来源与分析

指标矿区环境、资源开发方式、资源综合利用、节能减排、创新与数字化矿山与企业管理企业形象的指标值不能直接获取，而是邀请专家根据相关资料给出评估值。专家给出评估值的依据有冶金行业绿色矿山建设规范、作者作为主要研究人员参与者的地质调查项目《西南典型地区矿产资源综合评价与区划》、《西南地区矿产资源综合区划》、《矿产资源环境承载力评价研究》。收集专家给出的每座矿山关于每个指标的评估值，可以认为是犹豫模糊元素（表1）。

表1 犹豫模糊评估值矩阵Table 1 Hesitant fuzzy evaluation matrix

4 结果和讨论

4.1 犹豫模糊数据的拓展

在表1中，不同犹豫模糊元素中所含值的数量是不同的。不同类型的决策者往往会采取不同的方式对犹豫模糊元素进行拓展。保守型的决策者可能通过选取最小值到犹豫模糊元素中得到犹豫模糊决策矩阵（表2）；进攻型的决策者可能通过选取最大值到犹豫模糊元素中得到决策矩阵（表3）。如矿山KS04的评价指标X1的两个可能值{0.9，0.7}，若按照乐观准则应扩展为{0.9，0.9，0.7}，按悲观准则则扩展为{0.9，0.7，0.7}。

表2 悲观准则的犹豫模糊评估值矩阵Table 2 Hesitation fuzzy evaluation value matrix of the pessimistic criterion

表3 乐观准则的犹豫模糊评估值矩阵Table 3 Hesitation fuzzy evaluation value matrix of the optimistic criterion

为了分析两种拓展方式对评价结果的影响，只考虑评价指标权重相等的情况，评价结果见表4和图1。

图1 乐观准则下等权与不等权的评价结果Fig.1 Evaluation results of equal and unequal rights under optimism criterion

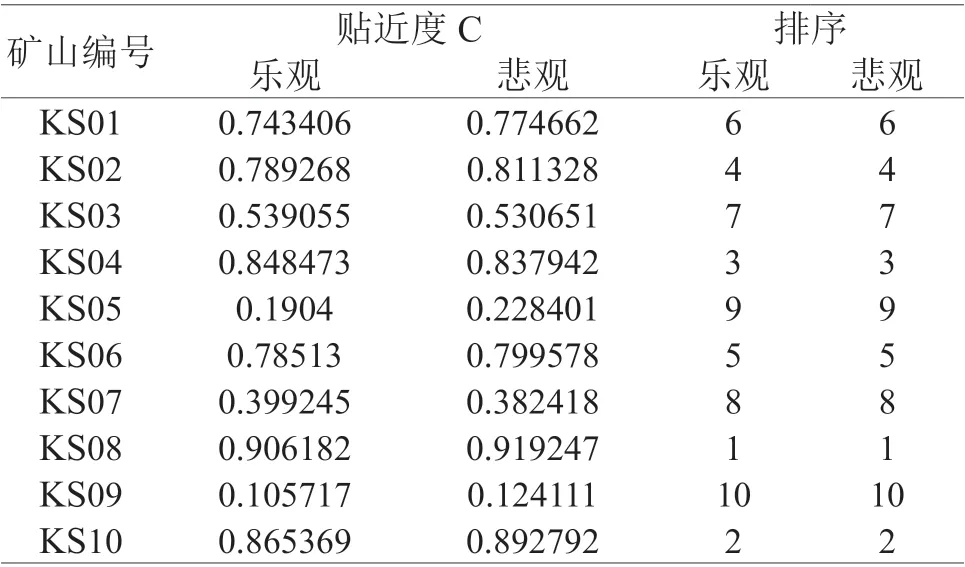
表4 不同准则的等权评价结果Table 4 Evaluation results of different criteria

从表4可知，根据悲观原则和乐观原则对犹豫模糊数据进行拓展，各矿山评价结果是一致的。

4.2 权重对结果的影响

评价指标权重对绿色矿山评价结果有影响。为了讨论权重的影响，采用上节中的两种方式对犹豫模糊元素进行扩展（表2、3）。通过求解较优化模型（式2），可以得到在不同扩展方式下的各评价指标的权重（表5）。不同的拓展方式下，评价指标X6的权值都是全部6个评价指标中最大的。事实上，较优化模型2是基于最大偏差法建立的，因评价指标X6的属性值有较大的偏差，所以被赋予了较大的权重。

表5 不同准则的各评价指标的权重Table 5 Weight of each evaluation index for different criteria

利用计算出的权重值，采用基于犹豫模糊欧氏距离的犹豫模糊TOPSIS方法，可得各矿山的排序（表6和图1）。①权值的影响：乐观准则下的各评价采用指标等权值与不等权值，除KS02与KS06矿山外，其余矿山的排序是一致的。悲观准则下的各评价指标等权值与不等权值，各矿山的排序是一致的（表6）；②拓展方式的影响：从表6的第8列与第9列可以看出，对各评价指标赋予不同的权值后，各矿山的排序一致的占全部矿山数的80%，不一致矿山数为20%。在乐观准则下，矿山KS02的排名是第5，在悲观准则下则排名第4。矿山KS06也有类似的情形。从不同角度的分析表明，评价指标的权值对绿色矿山建设水平的评价结果有影响。

表6 不同准则的不等权评价结果Table 6 Evaluation results of different distance measures

4.3 犹豫模糊距离对评价结果的影响

犹豫模糊距离测度是犹豫模糊集理论的一项重要研究内容，通过计算距离测度，可以方便的比较不同方案之间的相似性和差异性。为了讨论不同的距离测度在评价矿山绿色建设水平中的影响，分别采用HNHD、HNED、HNHH和HHNED等距离来计算各矿山的贴近度，再根据贴近度对各绿色矿山建设水平排序（表7）。

表7 不同距离的评价结果Table 7 Evaluation results of different distances

从表7的第4列至第9列可以看出，采用HNED、HNHH与HHNED时，根据悲观原则与乐观原则，各矿山评价结果是一致的；采用HNHD时，在乐观原则下有KS01、KS02、KS03、KS05与KS105座矿山的评价结果与后三座矿山距离的评价结果不一致。在悲观原则下有KS01、KS02和KS063座矿山的评价结果与后三座矿山距离的评价结果不一致。无论是在乐观准则还是悲观准则下，采用HNHD时矿山KS01的排名都比较高。