促进深度学习 凸显数学本质

彭文芳

摘 要：数学教学中促进学生深度学习，凸显数学本质，学生才能在学习中处于高阶思维的状态，从而思维能力得到发展。怎样促进学生深度学习呢？一是“巧设问题，实现知识的深度理解”，二是“经历过程，聚焦知识的深度建构”，三是“适时思辨，凸显思维的深度发展”，四是“适当延伸，促进知识的深度迁移”。数学深度学习，需要精心设计和科学引导，多种途径有机融通，才能让学生的学习更深入、更清晰、更合理，让学生的学习真正触及数学的本质，学习能力真正得到发展。

关键词：深度学习;问题;思维潜力;拓展迁移

深度学习是源于学生自身内部动机对有价值的学习内容展开准确、完整、深刻、丰富的学习。教师应引导学生运用批判思维学习新知，建构新体验，进而促进问题解决能力、批判性思维、创造性思维等高阶能力的发展。数学教学中凸显数学本质的关键是促进学生的深度学习。

一、巧设问题，实现知识的深度理解

问题是激发和引领课堂教学的重要推手，是撬动学生思维的杠杆。以问题驱动为主线的深度学习，是以问题驱动的形式让学生在学习过程中逐步走向知识的深入理解，是对知识内部意义的追寻和理解。学生通过解决逐层深入的问题，能实现对知识的重组与建构。因此，教师在教学中要设计有层次的问题，营造深度学习的氛围，促进深度学习逐层深入，实现知识的深度理解，触及数学的本质。

例如，教学“工地要运80吨黄沙。如果有下面3种货车选择：A货车载重量3吨，每辆运费65元;B货车载重量5吨，每辆运费60元;C货车载重量12吨，每辆运费70元，可以怎样设计运输方案？按你设计的方案，运这批黄沙一共要运费多少元？”教学时围绕以下四个问题引导学生思考：（1）如果你是工地老板，设计运输方案，你首先考虑以什么为标准？（省钱）（2）要想省钱，你怎么考虑？这个问题学生出现三种考虑：①一种都用80除以载重量老老实实算。②先比较三种货车中A和B车发现B货车量多钱还便宜，再比较B和C车，C车量翻倍而钱只增加少量，明显C车便宜，所以考虑先选C车。③求出三种货车每吨的运费，再比较，也发现C车便宜，所以也考虑先选C 车。（3）根据你列出的算式，你想到什么方案？（80÷12 = 6（輛）……8（吨））根据列出的算式的答案，这个问题学生得出三种方案：①考虑不浪费车的空间，选6辆C车、1辆A车和1辆B车;②考虑不浪费空间，选5辆C车和4辆B车;③考虑浪费空间却省钱，选7辆C车。（4）看三种方案算出的钱数，为什么第三种方案浪费空间最多还最省钱？这个问题有的学生说因为C车价格超便宜，有的学生说因为A车和B车各1辆合起来的钱比1辆C车贵多了……

以上四个问题，激发学生整合生活经验、整合数学知识，多角度分析问题、寻求多种思路，引导学生一步步将学习引向深入，帮助学生深度理解选择设计方案的有关知识、方法，使学生能灵活解决实际问题。

二、经历过程，聚焦知识的深度建构

数学本质是对数学概念的产生与发展、运算规则的形式和应用、问题解决等根本性的认识，课堂教学中学生经历知识产生、发展、应用的学习过程，经历数学问题的发现、提出、分析、解决的过程，是对数学本质全面的把握。经历过程的学习是引发深度学习的前提和根本，学生经历学习的过程，才能深度建构新知。

例如，“方程的意义”的教学。方程概念的建立，是小学阶段从算术思维转向代数思维的拐点，需要设置隐含代数思想的情境。方程用等式表示数量关系。要让学生体会方程“用等式表示数量关系”的本质特征，在教学过程中，通过设置具体情境帮助学生寻找相应的等量关系，构建“方程”的概念。

（1）情境引入，初步体会

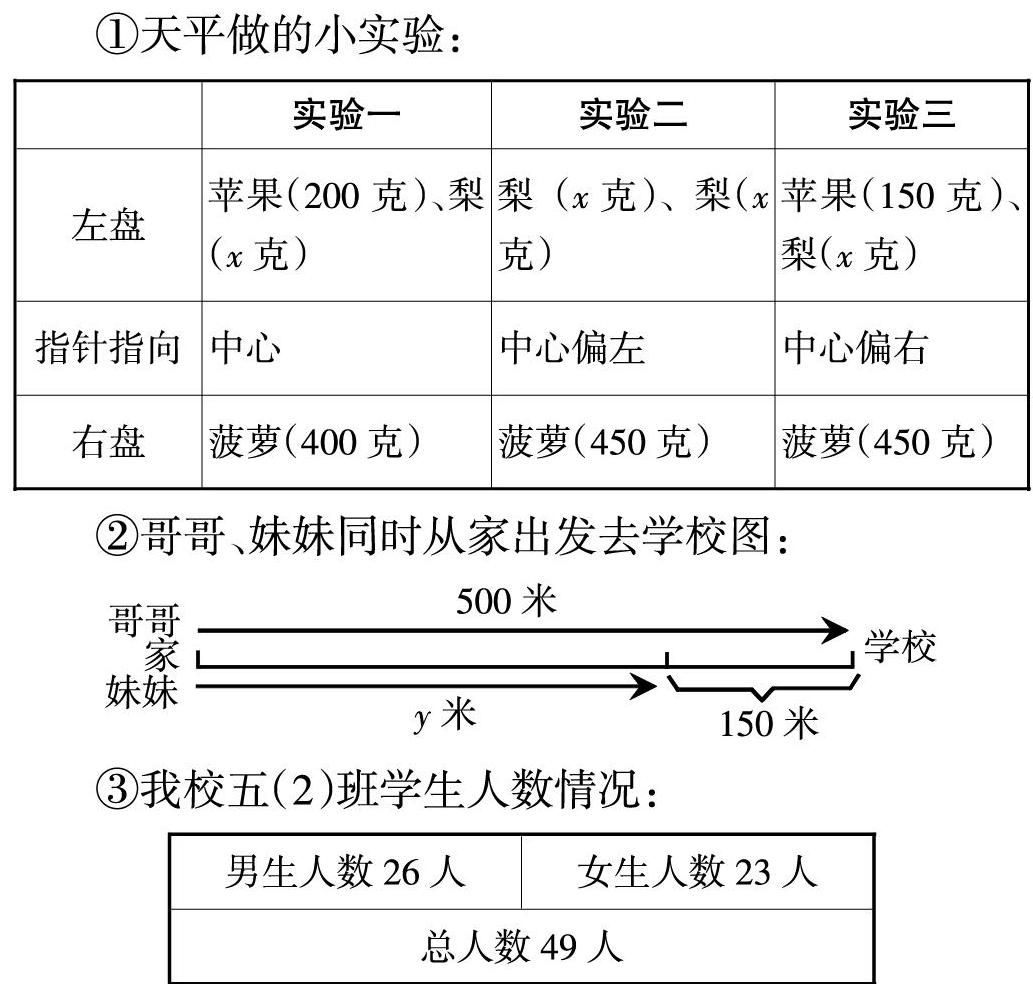
教学时出示以下三个情境：

①天平做的小实验：

②哥哥、妹妹同时从家出发去学校图：

③我校五（2）班学生人数情况：

学生依据三个情境展现说出数量关系，并列出式子。让学生感知“方程”与已有知识经验的联系，体会“方程”与等量关系的联系。

（2）分类梳理，建构概念

学生依据三个情境展现说出数量关系，并列出式子：①200+x=450②2x>450③150+x<450④500-y=150⑤150+y=500⑥26+23=49⑦a+26=50⑧7b=49，教师提出问题：你能给这些式子分类吗？学生有的分成两类：不相等的式子②③是一类，相等的式子①④⑤⑥⑦⑧是一类，有的分三类：不相等的式子②③是一类，相等的式子中含有未知数的①④⑤⑦⑧是一类，不含未知数的⑥又是一类。今天我们就来研究表示相等关系的式子。教师继续引导学生思考：比较这些式子，你发现了什么？

依据学生的回答揭示“方程的意义”。学生依据数量关系列出的式子进行分类梳理，逐步发现等式与方程的区别，抽象概括出方程的意义。

三、适时思辨，凸显思维的深度发展

思辨是指教师引导学生在分析、推理、判断、交流等思维活动中用数学方法从数学角度进行的思考和辨析。思辨可以帮助学生克服思维定式的消极影响，能引发学生的思维冲突，激发学生对问题进行深度思考的欲望。值得思辨的问题往往是知识的核心，也是教学的重点和难点，有思辨数学学习才有深度。因此，教学中教师要设计驱动学生思辨的活动，引导学生在思考、辨析中理解，促进深度学习的有效开展，引领学生思维深度发展。

“认识负数”一课，围绕“假如世界没有负数可以吗？”“0是正数还是负数”这两个话题，学生展开交流，学生在课堂中各抒己见。

1.纵向思辨，教师提出问题：“假如世界没有负数，可以吗？”生1：不可以没有负数，如果没有负数，零下的温度就没办法表示了。生2：不可以没有负数，如果没有负数，电梯地下一层没办法表示。生3反驳：可以没有负数，地下一层可以用字母A表示。生2回驳：如果地下100层呢？生3反驳：可以用“AB”“AABB”等来表示;生4回驳：用这么多字母表示你记得这些都表示哪一层吗……思辨“假如这个世界没有负数，可以吗？”的过程，学生从思辨“地下一层的表示”再到思辨“地下100层的表示”，思维不断深入，在思辨中感悟负数的产生给生活带来的方便，在思辨中学生的思维能力也得到发展。

2.横向思辨，教师提出问题：“0是正数还是负数呢？”生1：负数的前面都有个负号，0前面没有，所以是正数。生2： 因为正数都有对应的负数，而0却没有，所以0既不是正数也不是负数。生3： 正数比0大，负数比0小，0既不是正数也不是负数。生4：正数都表示一个值，而0不表示一个值，它又没有负号，所以0不是正数也不是负数……思辨“0是正数还是负数”的过程中，学生列举0不满足负数的多个特点来思辨，在思辨中学生对正数、负数有了更深入的理解，在思辨中学生的思维能力也得到发展。

在思辨的过程中，学生为了表明自己的观点，思维瞬间被激活，对信息进行判断、分析，并通过列举、推理、展示等方法验证自己的观点，大脑处于积极思考状态，思维潜力被充分挖掘，这样的过程使学生的学习走向深入，使学生的数学语言表达能力、逻辑推理能力和思维批判能力真正得到锻炼和发展。

四、适当延伸，促进知识的深度迁移

延伸拓展是指在原有知识基础上增加新的知识，或将原有知识进行延伸联系以解决新的知识。数学知识是互相关联的，教学不能局限和固守在某一节课或某一个知识点上，需要有整体意识，从知识关联的角度以整体化的方式把握数学知识本质，获得结构化和系统化的知识。

例如，在教学“方程的意义”时，出示下面巩固练习：“根据方程选题目：6m=300 ①每辆小汽车m元，6辆这样的小汽车一共300元。②一辆汽车每小时行驶m千米，这辆汽车6小时行驶300千米。”教师提出问题引导：选哪一个符合方程的等量关系呢？学生得出多种思考：选①， 因为单价×数量 = 总价;选②，因为速度×时间 = 路程，两个都可以选。教师继续追问：“6m=300在生活中还可以表示哪个等量关系？”学生得出多种思路：每天生产m个零件，6天生产300个;每班有m人，6个班300人……小结得出：方程在生活中有着不同的表現。一个根据方程选等量关系的练习就打通了这一类等量关系之间的联系，让学生感悟方程的不同表现形式，感悟它与以前学的算术理解的差异，拓宽了学生的思路，使学生深度学习持续发展，有效促进了学生学习的拓展迁移能力。

总之，数学深度学习，需要精心设计和科学引导，多种途径有机融通，才能让学生的学习更深入、更清晰、更合理，让学生的学习真正触及数学的本质，让学生的思维能力、学习能力真正得到发展。

参考文献：

[1]王冬晖.数学问题四驱动：小学数学深度学习的有效途径[J].新课程，2018（2）：266.

[2]金洁.聚焦学生经历 有效建构概念[J].教学月刊，2017（4）：46-49.