基于多复域的频响函数灵敏度分析

田 宇， 曹芝腑， 姜 东，

（1.南京林业大学 机械电子工程学院，南京 210037；2.东南大学 空天机械动力学研究所，南京 211189）

参数灵敏度分析在工程结构优化[1]、模型修正[2-4]和参数识别[5-8]中具有广泛应用。通过参数的灵敏度分析，可以量化工程结构中各设计参数对结构性能的影响程度和影响规律，指导结构设计和分析[9-10]。复杂结构的影响因素比较多，通过灵敏度分析可以将对结构性能影响较大的参数作为变量，从而降低结构分析设计难度，提升分析效率。

直接求导法通过对频响函数的模态展开式进行求导，得到频响函数灵敏度微分方程，该方法计算量较大，且存在由模态截断导致的频响函数分析误差。频响函数残差法是在实数域上进行参数摄动，在函数偏导数急剧震荡处或摄动量过小时，计算精度容易受摄动步长的影响。Lin[11]运用加权灵敏度法，在建模存在较大误差的情况下，依然可以得到收敛性好的频响函数灵敏度分析结果。Zhu等[12]基于Sherman-Morrison-Woodbury公式，提出了一种频响函数的再分析方法，利用该方法可以得到多参数同时摄动时的频响函数灵敏度，提高分析效率。黄修长等[13]基于频响函数综合的子结构方法推导了结构动力系统的灵敏度，提高了结构建模与优化设计的效率。周俊贤等[14]基于频响函数、模态、静力位移的灵敏度分析，对结构的局部损伤进行识别。Esfandiari等[15]提出了一种基于频率响应函数主成分变化和灵敏度分析的模型修正方法，用不完全测量的结构响应结合主成分分析得到灵敏度，该灵敏度分析方法比直接使用频响数据的结果更准确。Wang等[16]提出了一种基于频响函数灵敏度分析的优化方法，研究了频响函数在一定频带宽度约束下的桁架结构的动态尺寸优化问题。

复变量求导法通过提取复数域的虚部响应得到参数灵敏度，避免差分运算，可以得到高精度的一阶导数。Wang等[17]将复变量求导方法应用于弹簧质量系统的固有频率和振型的一阶导数的求解。Gao等[18]通过求解奇异函数和强非线性函数的偏导数，证明了复变量求导法得到的导数解精度远高于差分法。Garza等[19]运用复变量求导方法计算结构动响应的一阶和二阶灵敏度，与前向差分法和中心差分法的灵敏度分析结果相比较，说明复变量求导法不易受摄动步长影响。在频响函数灵敏度分析中，运用复变量求导法计算频响函数灵敏度更加高效精确。但由于频响函数本身含有复数，对设计变量再进行虚部摄动时，需要对方程本身的复域与摄动量的复域进行解耦，产生了不同复域下的虚数单位同时运算的问题。

本文提出了一种基于多复域的频响函数灵敏度分析方法，建立复数在实域中的等价矩阵格式，得到多复域下结构动力学方程与灵敏度方程的解耦形式，实现频响函数关于结构参数的灵敏度求解，为频域内结构动响应的灵敏度分析提供更加准确的数值求解方法。

1 理论基础

1.1 复变量求导法

复变量求导法是一种计算精度高且不受摄动步长影响的数值灵敏度求解方法，复数的定义为

式中:C1为所有单复数的集合；i1为虚数单位，=-1；R为所有实数的集合。在复变量求导法中，通过构造设计参数的虚部摄动量，利用复数域泰勒展开公式，可以得到其对应的一阶灵敏度

式中:θ为设计参数；h=Δh×θ为参数摄动量，Δh为摄动系数。

则式（2）的虚部响应可以表示为

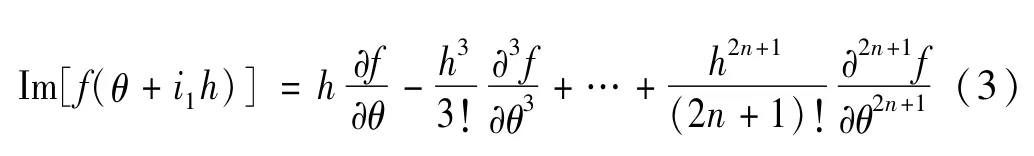
式中，Im（f）为函数f的虚部响应，最后得到θ的一阶偏导数可表示为

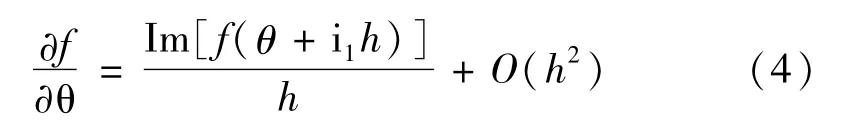
式中，O（h2）为摄动量的二阶截断。由式（4）可以看出，计算函数的一阶灵敏度时，对实函数的自变量摄动i h，求出复变函数的值，取其虚部再除以h，即可得到函数的一阶灵敏度，避免了极小数相减的问题。该过程可以解决一般解析分析无法解决的强非线性和隐函数偏导数计算问题，且一步即可完成计算，计算量比常规差分法更小。计算系统频响函数灵敏度时依然可以使用此方法。

1.2 复域的矩阵等价

在采用复数进行分析时，通常采用式（1）的形式构造计算方程。为了将复数的实部和虚部进行分离，可以采用实数域的矩阵形式得到复数域的等价格式。对同一个运算过程，矩阵形式的计算结果重新化为多项式形式后，与使用式（1）的多项式形式计算出的结果完全一致[20]。任何单复数都可以用一个2×2的实数矩阵表示。定义如下

式中，X1为单复数x0+x1i对应的矩阵表达形式，其每个元素与C1中的每个元素一一对应。

双复数的定义在单复数的基础上，含有两个不同方向的虚数单位。在所有的多复数中，双复数的性质是已知和研究最多的，并已经应用于多个应用领域，如分形和量子理论[21-22]。双复数可以用2×2的复数矩阵或4×4的实数矩阵表示，定义如下

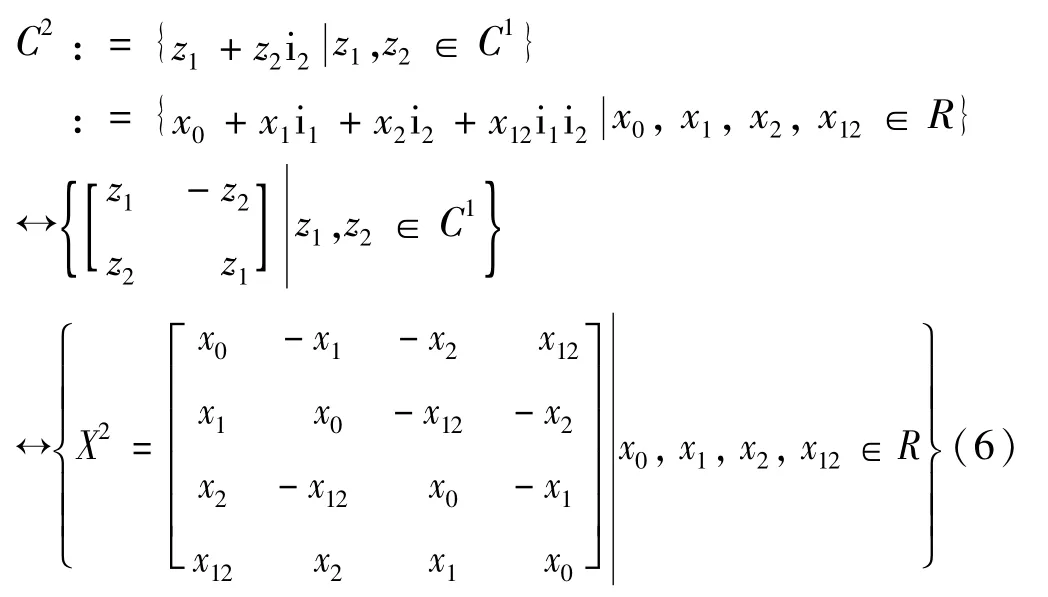
式中，X2中的每个元素与C2中的每个元素一一对应，任何双复数都可以用一个2×2的复数矩阵或4×4的实数矩阵表示。

每增加一个虚数单位，就要对矩阵进行一次扩维。含有n个虚数单位的参数，需要2n×2n维实数矩阵进行等价。

表示多复数的实数矩阵在文献[23]中称为柯西-黎曼矩阵，这种形式的柯西-黎曼矩阵与多复数之间存在一一对应关系。因此，多复数的算术运算（+，-，×）等价于矩阵表示上的算术运算。

1.3 多复域频响函数灵敏度分析

为了求解结构频响函数关于设计参数的灵敏度，考虑频域内结构的动力学方程中已有的i复域，引入仅考虑设计参数摄动的j复域，从而实现多复域下的频响函数灵敏度分析。

频域内结构的动力学方程为

式中:M，C，K分别为系统的质量矩阵、阻尼矩阵和刚度矩阵；i和j为虚数单位；ω为圆频率；θ为设计参数；x（ω）和F（ω）为位移与激励的傅里叶变换。

首先，对i复域内的结构矩阵进行等价转换。利用复数的等价矩阵表达，式（7）中各项的等价实数矩阵为

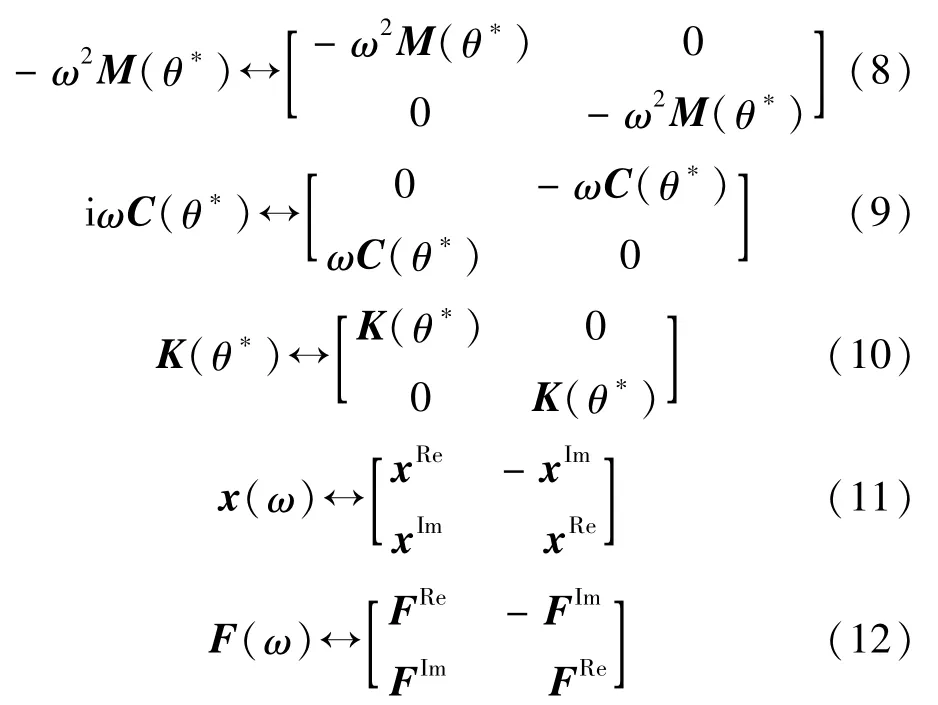
式中:xRe，xIm分别为x（ω）的实部和虚部；FRe，FIm分别为F（ω）的实部和虚部。 将式（8） ～式（12）代入式（7）可得

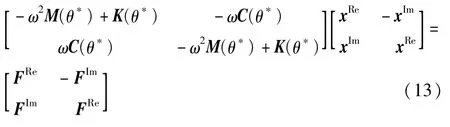
式（13）为四个等式构成的方程组，其中只有两个有效方程，舍去x矩阵与F矩阵的第二列，式（13）可简化为

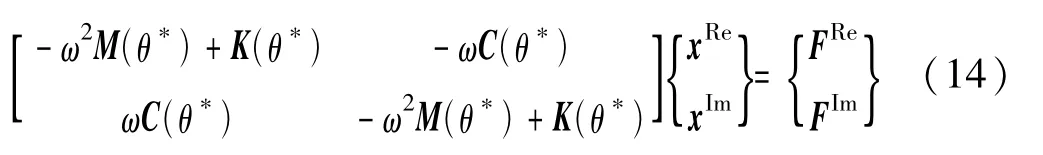
然后，考虑设计参数θ所在的j复域，再次利用复数的矩阵表达对j复域内的参数进行等价转换。将式（14）展开为j复域下的表达式

式中，ΔM，ΔC和ΔK分别为M，C，K的摄动量。利用双复数式（6），将式（15）转化为实数矩阵的表达

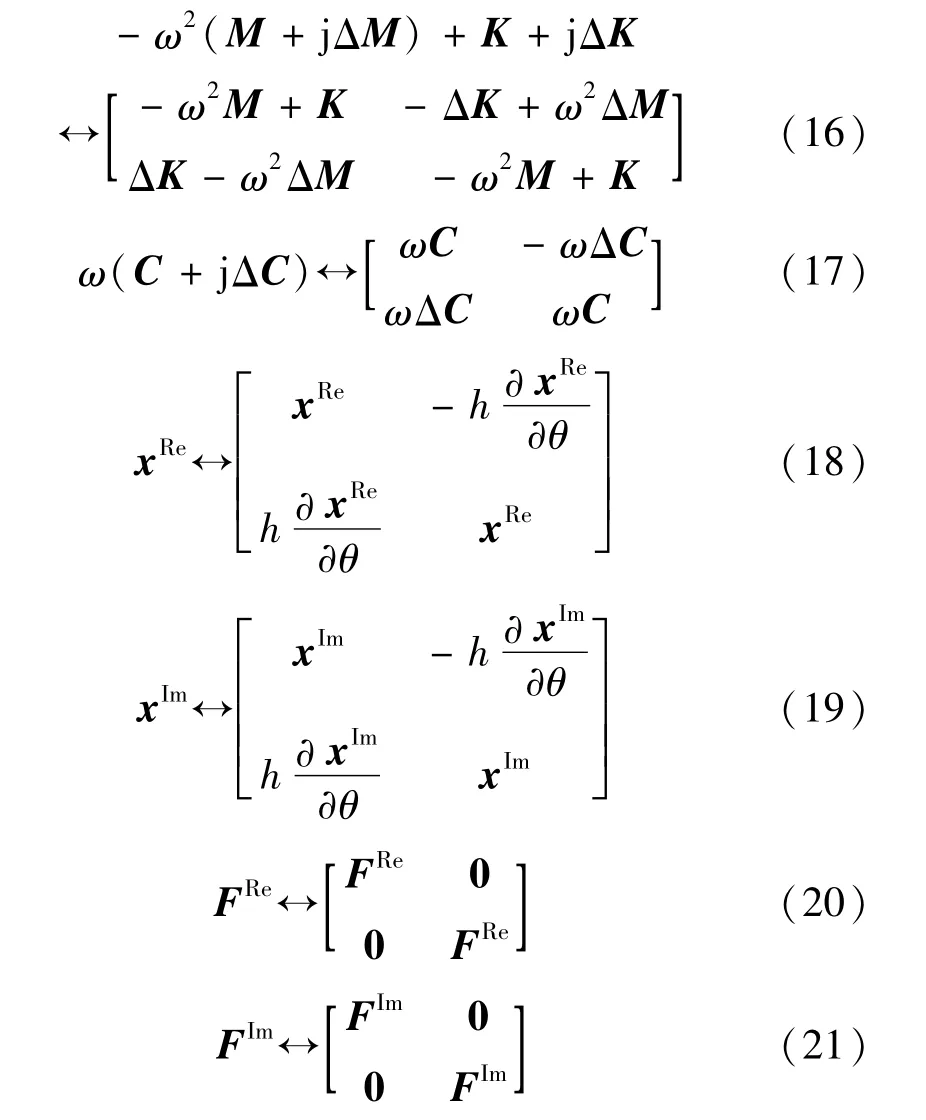
最后，通过在i复域和j复域上的二次转换，得到扩维后的控制方程式（22），即为频响函数对设计参数θ的灵敏度计算公式。

若对某设计参数的摄动只导致质量矩阵、阻尼矩阵和刚度矩阵中的某一个或两个矩阵发生变化，则只要将不发生变化的摄动矩阵ΔM，ΔC或ΔK变为零矩阵代入式（22）即可。

1.4 实现流程

基于多复域的结构频响函数灵敏度分析方法（见图1），按照如下步骤实现:

图1 多复域法频响函数灵敏度分析流程图Fig.1 Flow chart of sensitivity analysis of frequency response function in multicomplex domain

步骤1对结构进行动力学建模，得到结构的质量矩阵、阻尼矩阵、刚度矩阵和外部力向量，从而得到结构的频响函数方程；

步骤2构造设计参数的虚数摄动量，该虚数方向与频响函数自身虚数的方向不同，使设计参数从实数变为复数，结构质量矩阵、阻尼矩阵、刚度矩阵也变成对应复数量，频响函数函数方程变为多复数方程；

步骤3将摄动后的频响函数方程运用多复数理论进行扩维，得到等价的实数矩阵，并利用数值分析方法对该实数矩阵求解；

步骤4提取实数矩阵的运算结果，得到结构的实部响应和虚部响应，并可计算得到频响函数对设计参数的的实部灵敏度和虚部灵敏度。

2 算例研究

2.1 多自由度系统

为验证多复域方法灵敏度分析方法的有效性，用五自由度弹簧质量阻尼系统开展研究，结构如图2所示。

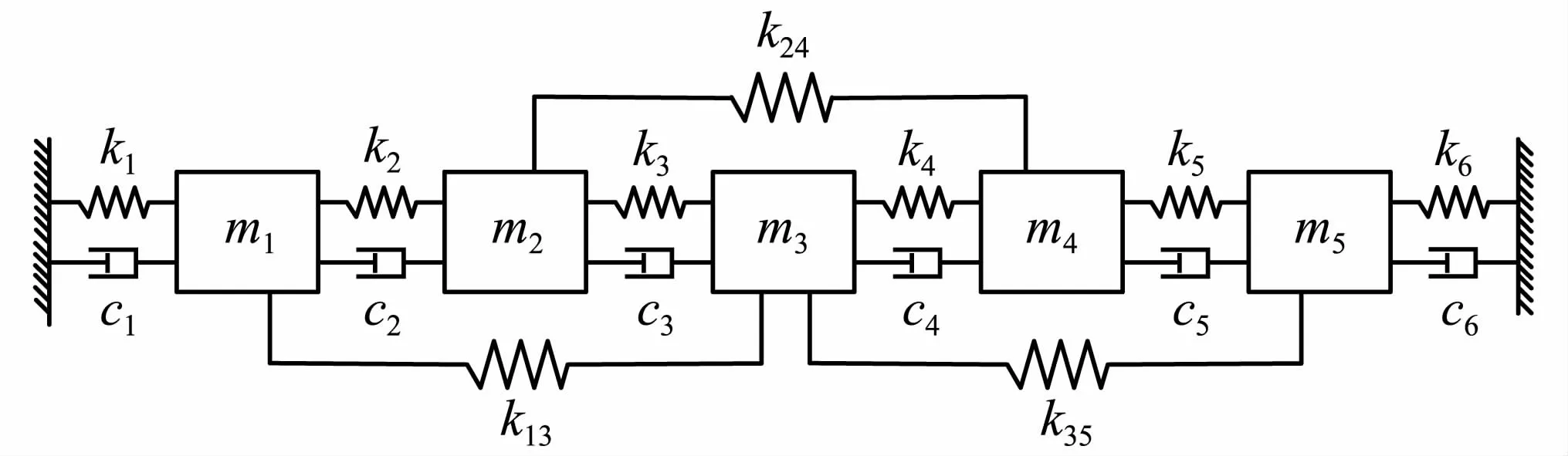
图2 五自由度弹簧质量阻尼系统Fig.2 Five degrees of freedom spring mass damping system

该系统两端固定，共有5个质量参数，9个刚度参数和6个阻尼参数，分析模型选取的参数值为m1=5 kg，m2=2 kg，m3=1 kg，m4=2 kg，m5=5 kg，c1=c2=c3=c4=c5=c6=0.5 N·s/m，k1=k2=k5=k6=100 000 N/m，k3=k4=50 000 N/m，k13=k24=k35=40 000 N/m。计算结构的幅频曲线，如图3所示。

图3 五自由度系统幅频曲线Fig.3 Amplitude-frequency curve of a five degree of freedom system

2.1.1 灵敏度分析

利用多复域法计算弹簧质量阻尼系统频响函数对结构参数的灵敏度。为了便于比较两种方法，选取合适的分析频段，先计算出系统的幅频曲线见图3。

由系统幅频曲线可知，该系统的一阶模态频率在110 Hz附近，为方便讨论，取频率范围108～112.5 Hz进行研究，分别给出系统频响函数幅值和频响函数对特定质量参数、阻尼参数、刚度参数的灵敏度。

记结构频响函数为Hlp，表示在第p个自由度上施加单位简谐力时第l个自由度的稳态位移频率响应。使用有限差分法和多复域法计算结构频响函数H11的幅值及实部、虚部响应对不同参数的灵敏度，摄动系数设为10-6。以频响函数的实部灵敏度为横坐标，虚部灵敏度为纵坐标，画出灵敏度的奈奎斯特图。结构频响函数幅值及频响函数的实部和虚部分别对质量参数、阻尼参数、刚度参数的灵敏度如图4所示。

图4中Am表示频响函数的幅值，图4（a）、图4（c）、图4（e）分别为结构频响函数幅值对质量参数m4、阻尼参数c1和刚度参数k1的灵敏度曲线，图4（b）、图4（d）、图4（f）为位移频率响应H11分别对质量参数m4、阻尼参数c1和刚度参数k1的实部和虚部灵敏度的奈奎斯特图。奈奎斯特图上每一点都是对应一个特定频率点下的频响函数灵敏度，横坐标和纵坐标分别为频率响应的实部灵敏度和虚部灵敏度。频响函数灵敏度更大的点计算误差也越大，更需要被关注，而频率-灵敏度图中绝大部分都为数值较小的点，误差大的部分难以被重点关注。奈奎斯特图中数值较小的点都集中在原点附近，数值越大的点距原点越远，变化较大的灵敏度在图中得到了很好的反映，精确度和误差也因此更容易比较。通过选取特定点计算响应对质量、阻尼和刚度的灵敏度，发现多复域方法是一种有效的方法，可以得出较为精确的灵敏度曲线，但精确度需要进一步探究。

图4 两种不同方法计算得到的频响函数灵敏度曲线Fig.4 Sensitivities of the FRF calculated by two different methods

2.1.2 摄动系数影响分析

为给出多复域法计算结果的精确误差，计算有限差分法和多复域法不同方法在摄动系数从10-1～10-7时与精确值之间的误差，以解析法的计算结果为精确值，给出频响函数灵敏度精确值的计算表达式（23）。

定义每次摄动后的灵敏度分析结果误差e为

表1 两种分析方法对于精确值的误差Tab.1 The error of the two analytical methods for the exact value

可以看出，多复域方法的误差明显小于有限差分法，具有更高的精度。画出两种方法在不同摄动系数时的灵敏度奈奎斯特图，如图5所示，通过图片更加直观地反应两种方法的误差。

图5 摄动系数对频响函数灵敏度的影响Fig.5 Influence of perturbation of two different methods on the sensitivities of the FRF

在摄动系数变小的过程中，有限差分法得出的刚度灵敏度曲线逐渐归一，误差逐渐减小。但在摄动系数过小之后，误差又开始逐渐增大。运用多复域方法计算刚度灵敏度在摄动系数到达10-2后，曲线迅速平稳，可以看出多复域方法收敛快，精度高。

2.2 桁架结构

进一步说明多复域灵敏度分析方法在复杂结构中的适用性，本文以GARTEUR AG-11[24]桁架结构为例开展频响函数灵敏度分析。

图6所示GARTEUR AG-11桁架结构的几何尺寸为宽3 m，长3 m×5 m，采用杆单元建立该结构的有限元模型，共划分为36个单元和32个节点，每个节点有两个自由度Zix和Ziy，节点编号与自由度编号如图所示。其中31和32号节点为边界节点，约束其全部自由度。结构的材料分别参数为:弹性模量E=7.5 GPa，密度ρ=2 800 kg/m3，横截面积A=0.004 m2。结构阻尼矩阵采用比例阻尼，设C=αM+βK，利用加权最小二乘法计算得出合理的α和β，取α=β=0.000 1。

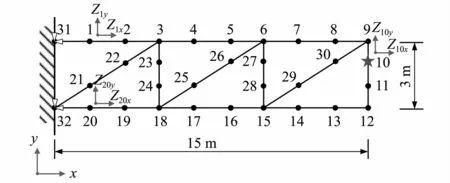
图6 GARTEUR AG-11桁架结构Fig.6 GARTEUR AG-11 truss structure

计算桁架结构在10号节点x向自由度Z10x的原点频响函数，记为H，其幅值曲线如图7所示。

图7 桁架结构频响函数幅值Fig.7 Amplitude of FRF of truss structure

2.2.1 灵敏度分析

桁架横截面积A是桁架结构的重要参数，决定桁架的刚度和质量。分析桁架频响函数对横截面积的灵敏度，可以为结构的优化设计和模型修正提供参考。桁架结构的横截面积是较为复杂的参数，横截面积的变化会引起系统质量矩阵、阻尼矩阵、刚度矩阵的变化。

在用公式表达弹簧质量阻尼系统的灵敏度分析的基础上，给出适用于更一般连续系统的方法。考虑连续结构如图8所示的简单杆桁架结构系统的质量、阻尼和刚度摄动。

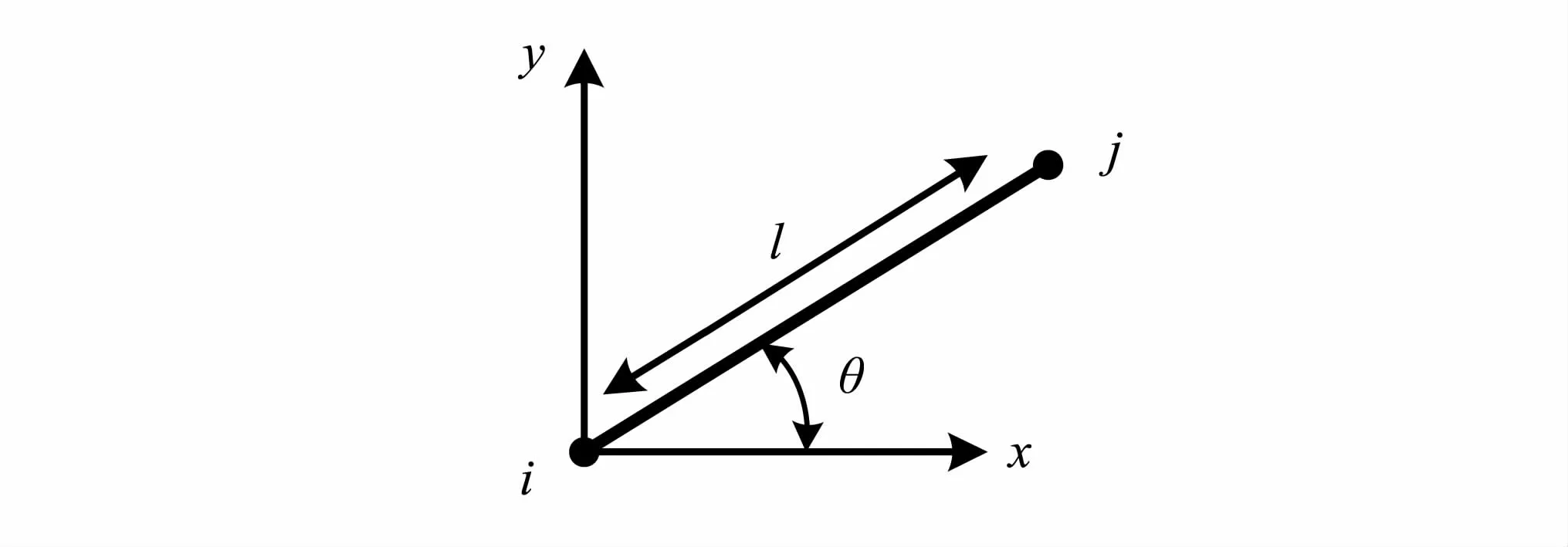
图8 桁架单元Fig.8 Truss element

图8为桁架结构的一个单位元素，单元两侧的节点用i和j表示，每个节点两个自由度，分别为x向和y向的平动自由度。则集中质量矩阵表示为

式中:上标t为单元编号；ρ为密度；A为横截面积；l为长度。单元刚度矩阵表示为

式中:E为弹性模量，每个子阵[kij]t维数为2×2。给定倾斜角度θ，则转换矩阵为

当总质量扰动为Δmi时，在节点i处的质量单元矩阵的单元局部坐标的变化量为

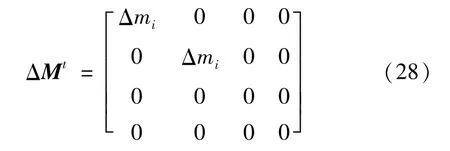
在全局坐标系中，质量单元矩阵的相应变化为

上面的形式可以写为

式中，上标T为矩阵转置，其中

由于质量矩阵组装性质，描述总质量变化的矩阵ΔM为

式中，Yij中的元素按节点编号排列，只有第（2i-1）个和第（2i-2）个对角元素非零。

如果将多个集中质量添加到多个节点，则由于集中质量只修改质量矩阵对角线上的元素，频响函数的灵敏度可以由此计算得出。类似式（32）要求在矩阵ΔM的对应位置添加变量值。

假设长度l保持不变，横截面积A作为变量，通过式（25）和式（26）影响质量矩阵和刚度矩阵。我们取单元t为例考虑横截面积变化情况:A^=A+ΔA。

单元t的横截面积变化ΔA时，其质量矩阵和刚度矩阵均发生变化。为了简化，设ΔA＞0，表示质量单元和刚度单元变化的矩阵为

则同理可知，将ΔA代入有限元分析计算，得出的质量矩阵M、刚度矩阵K即为所需的ΔM，ΔK。

在得到质量、阻尼、刚度矩阵的变化量ΔM，ΔC，ΔK后，代入式（22），采用多复域方法，得到Z10x的原点频响函数H关于横截面积A的实部和虚部响应灵敏度奈奎斯特图，如图9所示。从图中可以看出，本文方法得到的结果与有限差分法的结果一致，对于复杂桁架结构，横截面积A的变化同时引起质量矩阵、阻尼矩阵和刚度矩阵的变化，该情况下多复域方法仍然有效。

图9 摄动系数为10-5时多复域方法的灵敏度分析结果Fig.9 Sensitivity analysis results of multicomplex domain method with perturbation of 10-5

2.2.2 灵敏度影响因素

为探究多复域方法对复杂结构进行灵敏度分析时的准确性和有效性，考虑摄动量对该方法计算精度的影响。分别使用有限差分法和多复域法，将摄动系数从10-1变化到10-8，计算频响函数H对设计参数横截面积A的灵敏度，并用式（23）和式（24）计算出精确值和误差e，结果如图10所示。

图10 摄动系数对有限差分法与多复域法计算频响函数灵敏度的影响Fig.10 The influence of perturbation coefficient on the sensitivity of FRFs by finite difference method and multicomplex domain method

多复域法和有限差分法在摄动量变小的过程中，误差都逐渐收敛。但有限差分法计算结果在摄动系数到达10-6后开始产生波动，在10-8处产生了剧烈变化，精度明显下降，而与之相对应的多复域法仍然稳定。

3 结 论

本文提出了一种多复域的结构频响函数灵敏度分析方法，通过实数域的矩阵格式对复数的实部和虚部进行分离，实现了复变量求导法在结构频域响应灵敏度分析中的应用，并通过多自由度系统和GARTEUR结构进行参数研究，证明了该方法的有效性。

相较于传统的实数域有限差分法，本文给出的一种多复域灵敏度分析方法保留了复数域灵敏度分析方法的优点，计算精度高，不受摄动步长影响，可以为频响函数灵敏度分析提供更加准确的结果。本文仅针对方程中存在两个复域的情况进行了研究，若存在更多复域时，可对方程进行多次扩维，用以一次摄动多个参数或求更高阶灵敏度，对此该方法依然有效。