六自由度机械手静力学分析

2021-10-11毕方淇王文丽张立凯陈金利张荣彬

装备机械 2021年3期

□ 毕方淇 □ 王文丽 □ 张立凯 □ 陈金利 □ 蒋鑫 □ 张荣彬 □ 李志

淄博市农业机械研究所山东淄博 255000

1 分析背景

近年来,工业机器人在各行各业应用和普及,极大促进了我国迈入工业4.0的智能化进程。在这一过程中,机器人的研究应用占据重要位置。机器人是我国智能装备、智能农业的重要基础和组成部分,但我国机器人研究起步较晚,技术相比国外还有一定差距,我国对机器人的研究依然任重而道远[1-4]。

六自由度机械手是一种较为常见的工业机器人,有较为严格的工作精度和结构刚度要求。对六自由度机械手各零部件进行研究,获得相应零部件的刚度、应力、应变情况与变化规律,对确保六自由度机械手稳定运行有重要作用。

在文献[5-6]所进行的机械手分析中,采用的分析模型过于简化,模型中未提供机械手内部结构,较难反映机械手受力后的真实情况。樊炳辉等[7]分析的机械手自由度较少,与六自由度机械手结构有较大差异。文献[8-9]所做研究与笔者所分析的六自由度机械手结构差别较大,且针对六自由度机械手框架式零部件的结构验证与分析较少。

笔者以典型六自由度机械手为研究对象,应用SolidWorks软件建立几何模型,应用Workbench软件进行静力学分析,获得六自由度机械手大臂和小臂刚度、应力、应变云图,验证六自由度机械手零部件的合理性,为后续设计和改进提供数据参考。

2 力学理论

根据六自由度机械手受力情况,其零部件受力后变形为弹性变形,不应出现塑性变形。由此,仿真分析中涉及弹性力学平衡微分方程、几何方程和物理方程[10]。

2.1 平衡微分方程

平衡微分方程为:

(1)

式中:σx、σy、σz为主应力;τxz、τyz、τyx、τzx、τxy、τzy为切应力;x、y、z为单位体积上作用的体积力F在三个坐标轴上的分量。

2.2 几何方程

几何方程为:

(2)

(3)

式中:u、v、w为表征质点相对于三个坐标轴方向的位移量;εx、εy、εz为主应变;γxy、γyz、γzx、γyx、γzy、γxz为切应变。

2.3 物理方程

物理方程为:

(4)

式中:D为弹性矩阵;E为弹性模量;μ为泊松比。

3 几何模型结构

六自由度机械手的结构较为复杂,需要考虑完整支撑、旋转、连接、固定等功能。虽然有限元仿真时需要对六自由度机械手的结构进行简化,但是设计过程中应对六自由度机械手的结构进行完整、详尽设计。六自由度机械手几何模型如图1所示。

图1 六自由度机械手几何模型

4 网格划分

根据六自由度机械手几何模型,对六自由度机械手的大臂和小臂单独建模,如图2所示。

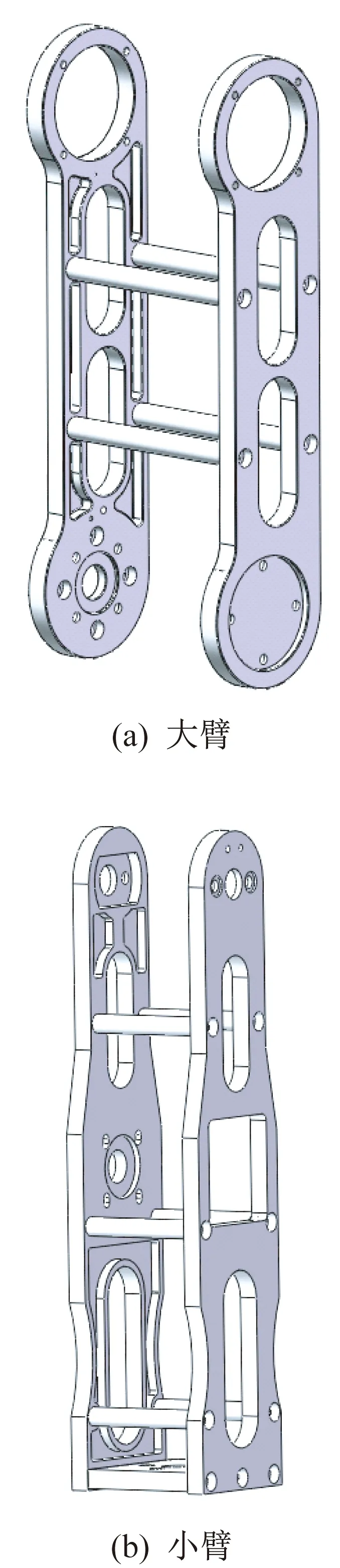
图2 结构单独建模

为保证有限元网格划分的精度和经济性,对大臂、小臂模型进行如下简化:

(1) 将倒角和倒圆角简化为直角;

(2) 将孔底118°锥角简化为平面;

(3) 大臂、小臂左右侧板与直杆之间无间隙;

(4) 对某些不影响结构强度的较薄位置适当加厚,以减少网格数量。

网格划分时,网格大小为5 mm,划分方式为自由划分。网格划分参数见表1。

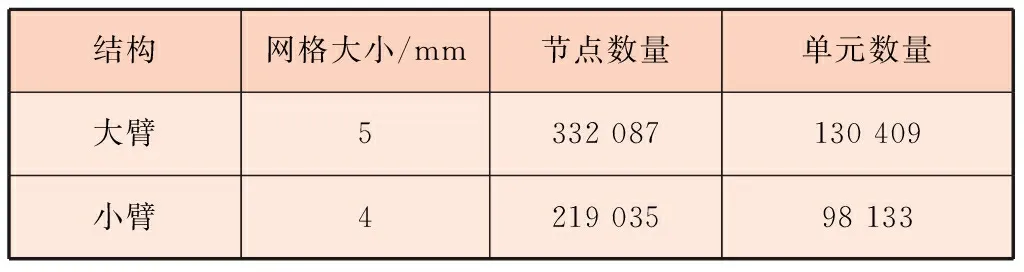
表1 网格划分参数

大臂、小臂模型网格划分后的局部情况如图3所示。

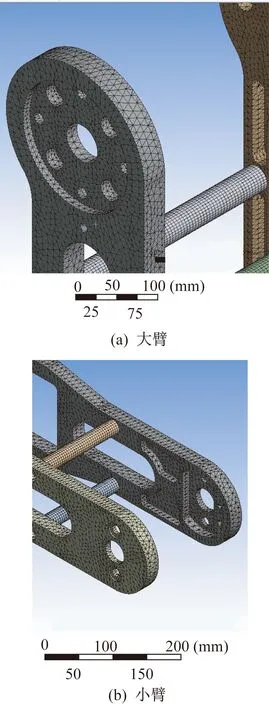
图3 模型网格划分

5 静力学分析

大臂、小臂的材料为铝合金,力学参数见表2。

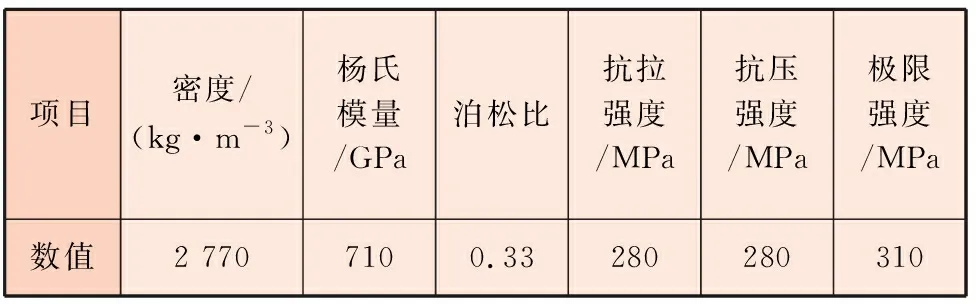
表2 铝合金力学参数

分别按照大臂和小臂在水平、竖直两个方向极限位置施加静力载荷[5],载荷大小为后续结构质量。根据重力方向,将不同方向的载荷乘以负载因数2.4,分别施加给大臂和小臂。经计算,大臂的质量为46 kg,则其受力为1 081.92 N;小臂的质量为11 kg,则其受力为258.72 N。

固定大臂和小臂与上一级结构活动关节部位,在大臂和小臂关节端分别施加载荷。

水平放置的大臂刚度、应力、应变云图如图4所示,竖直放置的大臂刚度、应力、应变云图如图5所示。

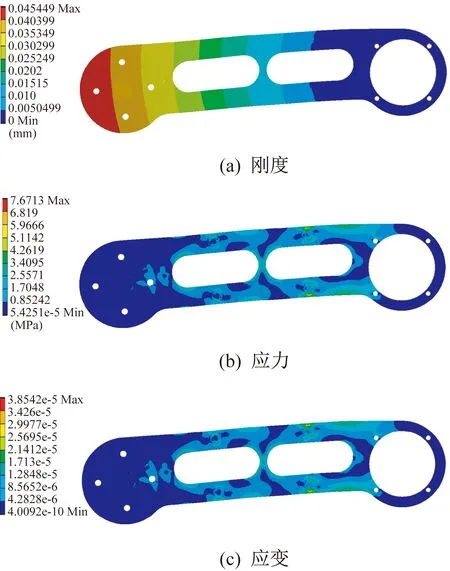
图4 大臂水平放置分析云图

图5 大臂竖直放置分析云图

水平放置的小臂刚度、应力、应变云图如图6所示,竖直放置的小臂刚度、应力、应变云图如图7所示。

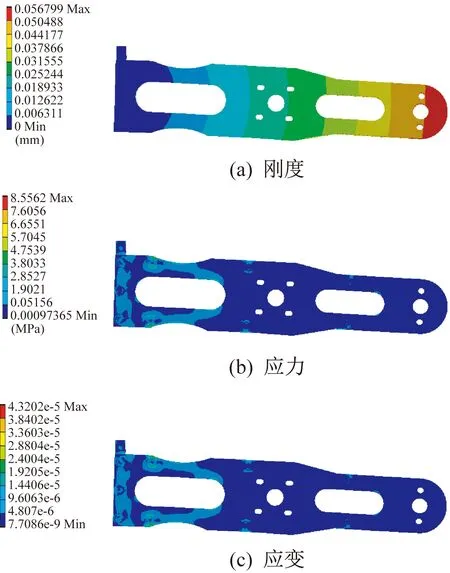
图6 小臂水平放置分析云图

图7 小臂竖直放置分析云图

根据分析结果可以看出,大臂和小臂在水平或竖直方向受力时,刚度均较好,大臂在水平放置时最大变形为0.045 mm,小臂在水平放置时最大变形为0.057 mm,可以满足零部件使用要求。对大臂和小臂的应力、应变进行分析,可以得到应力、应变均在安全范围内,最大应力出现在螺栓沉头孔边缘尖锐处,在此处增加倒角或倒圆角,可以有效改善应力分布。通过分析确认,大臂和小臂可以满足使用要求。