跨模态检索中的相似性漂移问题*

郑奇斌，刁兴春，王彦臻，曹建军，刘 艺，秦 伟

(1. 陆军工程大学 指挥控制工程学院， 江苏 南京 210007； 2. 军事科学院， 北京 100089；3. 军事科学院 国防科技创新研究院， 北京 100071； 4. 天津(滨海)人工智能创新中心， 天津 300450；5. 国防科技大学 第六十三研究所， 江苏 南京 210007)

随着多媒体、互联网和大数据等技术的迅速发展，文本、图像等不同模态的数据迅速涌现[1]。不同模态的数据结合在一起，显示出较单模态数据更加丰富的自然和社会属性[2]。而近年来机器学习等技术的发展使得综合利用多模态数据成为可能，特别是得益于深度学习技术的发展，跨模态检索[3]、视觉问答[4]、跨模态推理[5]等多模态应用取得了巨大的进步。

跨模态检索旨在发现不同模态(除少数工作，如文献[6]涉及两种以上模态的数据，大部分研究都聚焦于文本和图像两种模态)数据对象间的相似关系，例如通过文本描述检索具有相似语义的图像，或通过图像检索具有相似语义的文本[7]。由于不同模态数据的表征是异构的，其相似度难以直接计算，通常需要将文本、图像等数据映射到目标表示空间或一个公共表示空间中[2-3]。现有研究通过典型相关分析[7-11]、主题模型[12-14]、稀疏表示[15-16]等方法实现跨模态映射，而近年来基于深度学习的方法[6, 17-22]由于其优异的性能成了主流。

尽管以上方法各不相同，但其中采用的映射函数形式几乎是线性变换或深度神经网络，并通过相应的损失函数学习其具体参数。其中，最常见的损失函数是最大边界损失[17, 23]，此外还有对抗型损失[24]、最大似然估计损失[25]等。这些损失函数的目的是使跨模态映射函数能够同时保持对象的模态内和模态间近邻关系。然而实际中由于训练数据不足等原因，并不能保证学习到的映射函数可以完全跨越模态间的障碍。Collell和Moens[26]对线性变换和深度神经网络的跨模态映射能力进行测试，发现其对模态内近邻关系的保持较好，而对模态间近邻关系的保持存在缺陷。

在此基础上，本文发现常见跨模态函数存在“相似性漂移”问题——映射函数对模态间近邻关系的保持能力与邻域的大小相关，在较小的邻域内近邻结构与真实近邻保持一致；而当邻域变大时，映射函数的近邻保持能力迅速降低。“相似性漂移”问题的存在会增大跨模态检索中误匹配的概率，降低其准确性。为了降低其影响，本文提出了一种基于“邻域传播”的匹配策略——通过样本的模态内近邻替代它自身，在映射空间中的较小邻域中进行跨模态相似样本的匹配。

本文首先介绍常见的跨模态映射函数，并引出其“相似性漂移”问题；然后，提出基于“邻域传播”的匹配策略，在不改变跨模态映射函数的条件下，降低“相似性漂移”问题对跨模态检索精度的影响；最后，通过在真实数据集上的实验分析，对“相似性漂移”问题的存在性以及匹配策略的有效性进行验证。

1 映射函数与“相似性漂移”问题

跨模态检索任务是找到待查询对象xi∈X在目标集合的跨模态近邻yi∈Y，为计算任意跨模态对象间的相似度，可以通过映射函数f:X→Y或g:Y→X将源对象映射到目标对象的表示空间[7]。构建跨模态映射函数的过程中，通常需要f和g能够同时保持对象的模态内近邻关系和模态间近邻关系。以f为例，为了在目标空间中保持模态间近邻关系，对任意xi∈X和yi∈Y，映射f需要满足：

(1)

式(1)表示如果不同模态的样本xi和yi相似，则通过f将xi映射到Y中后，f(xi)和yi的距离应小于δ。

同时，为了保持模态内对象的近邻关系，映射f还需要保持X的模态内近邻关系：

(2)

式(2)表示如果同模态对象在原始表示空间中距离较小，在映射后它们的距离仍然要保持足够小；反之，如果同模态对象在原始表示空间中差异较大，在映射后它们的距离仍然要保持足够大。由式(2)可以进一步导出：

(3)

式(3)说明为了保持模态内关系，f必须为Lipschitz连续的，其中KX> 0为Lipschitz常数。现有研究中最常用的线性变换

f(x)=W0x+b0

(4)

以及深度神经网络

f(x)=W1σ(W0x+b0)+b1

(5)

都满足上述条件。其中，W0和W1为线性映射矩阵，b0和b1为偏置，σ为非线性映射函数。为了使映射f能保持对象间的近邻关系，实际中经常通过最小化最大边界损失(max-margin loss)[17]来学习f：

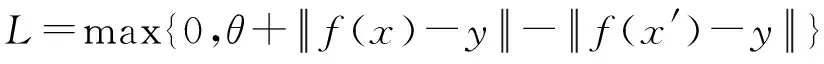
(6)

其中：θ为边界；x,y为相似的样本对；x′,y为不相似样本对。

尽管深度神经网络具有强大的学习能力，但是因为训练数据不足等原因，想要在跨模态映射中“完美”地保持模态内近邻关系和模态间近邻关系并非容易。Collell和Moens[26]通过在不同多模态数据集上的实验证明，尽管现有方法都致力于在跨模态映射中保持样本的近邻关系，但是最终学习到的映射函数并不能很好地保持样本的模态间近邻关系：主流的线性变换和深度神经网络更倾向于保持模态内近邻关系，而对模态间近邻关系的保持较差。因此，相似的跨模态样本经过映射后不一定保持靠近，而不相似的跨模态样本却可能接近，从而导致检索的准确率下降。

Collell和Moens[26]提出平均近邻覆盖率(mean Nearest Neighbor Overlap，mNNO)来度量跨模态映射对近邻关系的保持能力，给定两个一一配对的对象集合V和Z，mNNO定义为：

(7)

其中，索引相同的vi∈V及zi∈Z为匹配的对象，N为数据集V和Z的对象总数，NNK(vi)和NNK(zi)分别为vi和zi的K近邻对象索引集合。mNNO通过计算映射前后对象的平均K近邻结构覆盖率来度量映射f对近邻结构的保持能力，mNNO(X,f(X))表示模态内近邻覆盖率，mNNO(Y,f(X))表示模态间近邻覆盖率。mNNO越高，则通过f进行映射后，匹配的准确率也会越高。

mNNO对不同粒度(由K值体现)的近邻覆盖率取平均值，从整体上度量跨模态映射对近邻关系的保持能力，而本文发现在不同的K值下，映射函数的模态间近邻保持能力是变化的：当K较小时，样本在映射空间中的跨模态近邻和真实近邻的覆盖率较高；随着K变大，跨模态近邻覆盖率迅速下降。本文将这种映射函数对模态间近邻关系的保持能力随邻域变化的现象称为“相似性漂移”，如图1所示。

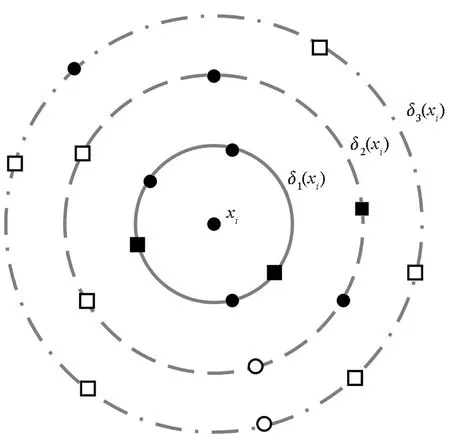
图1 相似性漂移问题示意Fig.1 Illustration of similarity drifting

图1中展示的是xi在映射空间Y中的近邻结构，其中圆点表示xi同模态近邻在Y中的象，方形表示其跨模态近邻，实心表示真匹配，空心表示误匹配。由于映射函数的“相似性漂移”问题，在映射空间中的同模态近邻大部分为真匹配；而跨模态近邻中误匹配较多。此外，图1中随着邻域δ的增大，发生误匹配的概率逐渐变大。这是由于对象间的相似性经过跨模态映射f后难以完全保持，并且其失真程度随着相似性判定的粒度增长(也就是邻域的扩大)而迅速升高。

跨模态映射函数的“相似性漂移”问题显然会增大误匹配发生的概率，并降低跨模态检索的准确性。

2 基于邻域传播的匹配方法

由于跨模态映射函数的“相似性漂移”问题，映射空间中样本的模态间近邻关系难以保持。而相对模态间近邻关系，包括线性变换和深度神经网络在内的映射函数都可以较好地保持样本的模态内近邻关系。此外，映射函数对模态间近邻结构的保持能力是随着邻域的增大而降低的，当邻域较小时，映射函数可以较好地保持模态间的近邻关系。因此，可以借助样本xi同模态近邻在映射空间的象，在其较小邻域中进行近邻匹配，进而降低“相似性漂移”造成的影响，得到更加准确的匹配结果。综合上述讨论，本节提出一种基于“邻域传播”的匹配方法，其基本思想如图2所示。

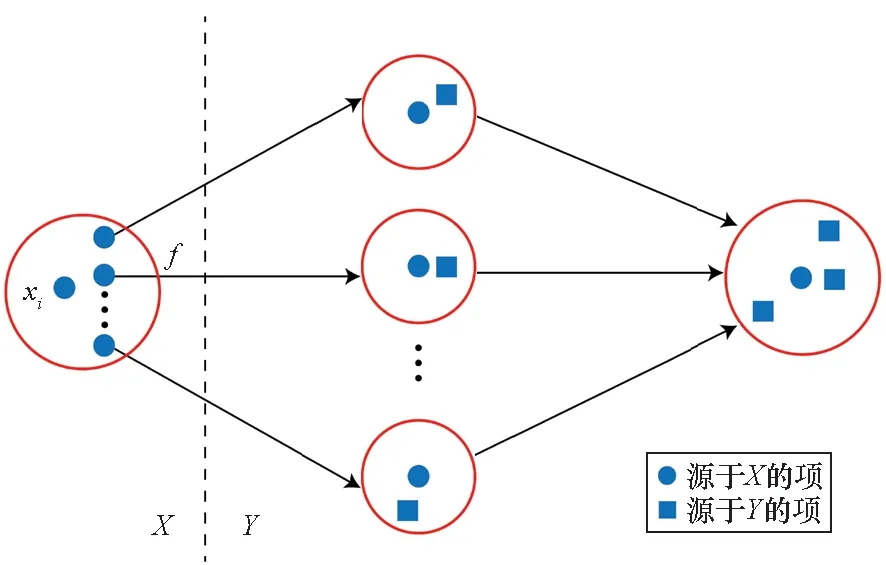
图2 基于邻域传播的匹配示意Fig.2 Illustration of neighbor-propagation matching

不同于传统方法直接通过f将xi映射到Y空间中后再进行相似度匹配，图2为了寻找样本xi的跨模态相似样本，首先通过给定的阈值τ在表征空间X中筛选同模态相似样本；然后利用f将这些样本投影到Y空间中，并在Y空间中这些样本的邻域内进行近邻匹配，选择每个样本的最近邻作为各自的跨模态相似样本；最后将上述结果求并集，得到样本xi的所有跨模态相似样本。上述过程可以形式化为：

(8)

其中，yl∈Y为目标项集中第l项，s为相似度函数(本文中使用余弦相似度)。模态内相似度阈值τ决定了匹配的粒度，本文中由用户根据其对准确率、召回率的偏好，以及数据的分布来决定。详细步骤见算法1。

算法1 邻域传播匹配

首先，利用现有方法学习跨模态映射函数f(例如，通过式(6)中的最大边界损失学习式(5)中的深度神经网络作为映射函数f)；然后对每个待查询对象qi，筛选所有相似度大于阈值τ的模态内近邻qj(j≠i)，并利用学习到的函数f将其映射到目标空间中后，选择T中与qj的相似度最高的tj作为查询对象的匹配对象，并将(qi,tj)加入匹配结果集合中。

设|Q|=n，|T|=m不考虑步骤1中跨模态映射学习的复杂度，上述算法的复杂度为O(n2m)。其中，查询集中共有n个待查询项；对每个待查询项，根据阈值τ过滤其近邻的复杂度为n-1，相似度高于阈值的最多为n-1个，而查询每个近邻在目标项集中的最近邻复杂度为m，则整个算法的复杂度为O(n×(n-1)×m)=O(n2m)。

3 实验分析

为了验证“相似性漂移”问题以及基于邻域传播的匹配策略，本节在真实数据集上对二者进行了实验分析。

3.1 数据集和实验设置

数据集及特征提取: IAPR TC-12[27]，Wikipedia[7]，训练集和测试集按照4 ∶1的比例划分。其中，图像的特征通过预训练神经网络模型VGG[28]提取，而文本的特征通过双向门限循环单元网络(Bi-directional Gated Recurrent Unit，Bi-GRU)[29]提取。

跨模态映射：分别通过式(4)中的线性变换[21](记为Linear)，及式(5)中的前馈神经网络完成。与文献[26]一样，W0和W1的初始参数产生自均匀分布[-1,1]，b0和b1初始化为0，非线性映射σ采用分别采用ReLU[20]、TanH[30]、Sigmoid[23]三种激活函数，网络的深度为五层。

实验中主要验证两个问题：

1)“相似性漂移”问题验证：利用线性变换和深度神经网络对不同数据集上的文本和图像数据进行跨模态映射，通过计算不同邻域的平均最近邻覆盖率[26]，分析跨模态映射对模态间关系保持能力和相似性粒度之间的关系，验证“相似性漂移”问题的存在。

2)“文本-图像”匹配方法验证：对相似性匹配方法在文本和图像的双向匹配任务中的表现进行比较，验证邻域传播匹配的有效性。其中，直接通过对象自身相似度阈值进行匹配的方法记为TH，本文提出的邻域传播匹配方法记为NP。

通过线性变换和深度神经网络进行跨模态映射，然后通过余弦相似度执行文本到图像以及图像到文本的相似度计算和匹配，并通过准确率(Precision)、召回率(Recall)指标进行对比：

(9)

(10)

其中，TP指正匹配对象的数量，FP指误匹配对象的数量，FN指未匹配到的正确对象数量。此外，为了更加直观地体现方法间的性能差异，还计算了曲线的AUC(area under curve)值，也就是曲线与坐标轴围成的面积。

3.2 最近邻覆盖率测试

本节的实验中，分别测试在给定不同最近邻参数K的条件下，线性变换(记为Linear)和深度神经网络(同文献[26]，激活函数使用ReLU，记为NN)在跨模态映射中对模态内关系(记为f(X),X)和模态间关系(记为f(X),Y)的保持能力，包括文本到图像(记为I2T)以及图像到文本(记为T2I)两个方向，以余弦距离(记为Cos)和欧式距离(记为Euc)为相似性度量。两个数据集上的平均最近邻覆盖率测试结果如图3～6所示。

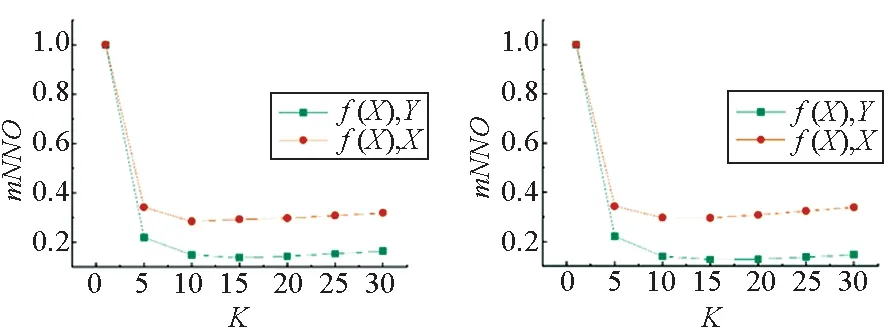
(a) I2T_linear_Cos (b) I2T_NN_Cos

图3所示为Wikipedia数据集中图像-文本的平均近邻覆盖率，经过两种跨模态映射后，图像模态内对象近邻结构覆盖率较高，而图像到文本的跨模态近邻覆盖率较低。此外，模态内近邻和模态间近邻的覆盖率随着K的增大，呈现降低的趋势。

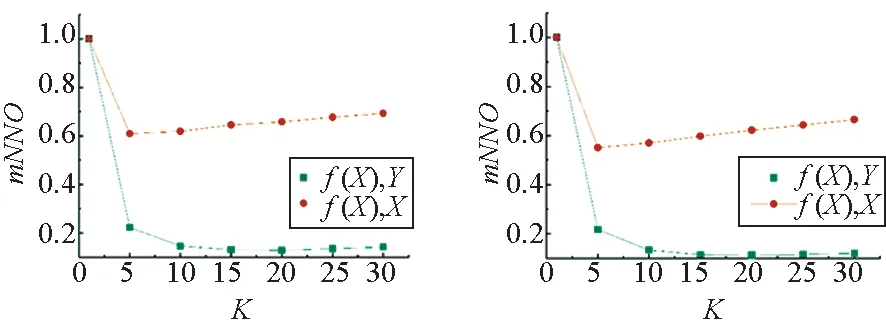
(a) T2I_linear_Cos (b) T2I_NN_Cos

图4所示为Wikipedia数据集上文本-图像的平均近邻覆盖率结果。跨模态映射对Wikipedia数据集的文本数据的模态内近邻结构保持能力更高(高于图像数据约0.2)。此外，当K=1时，该数据集的模态内和模态间的近邻覆盖率同样保持最高，而随着K的增大，模态间平均近邻覆盖率仍然随之降低，但模态内近邻覆盖率在降低之后有轻微回升。

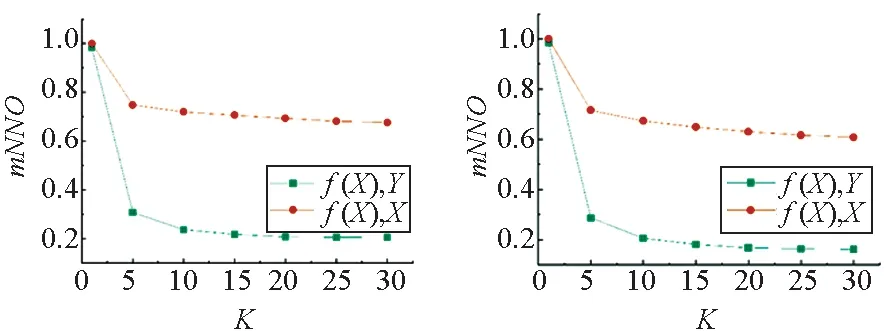
(a) I2T_linear_Cos (b) I2T_NN_Cos

图5为IAPR TC-12数据集中图像-文本的平均近邻覆盖率，可以发现，通过线性变换或者神经网络将图像数据映射到共同空间中后，无论使用余弦距离还是欧式距离，两种跨模态映射对模态内关系的保持能力要高于对模态间关系的保持能力。并且，无论对图像到图像的模态内保持，还是图像到文本的模态间保持，其平均覆盖率当K=1时最大，而随着K的增长，很快下降到一个稳定的值。

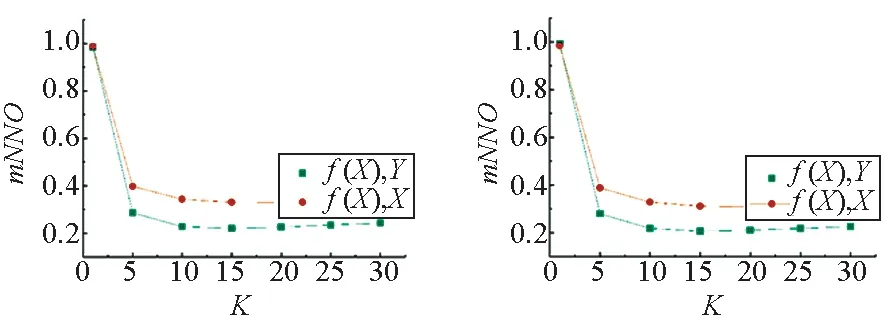
(a) T2I_linear_Cos (b) T2I_NN_Cos

在图6的IAPR TC-12数据集上文本-图像的平均近邻覆盖率测试中，线性变换和深度神经网络同样倾向于保持模态内近邻关系，但是二者的差距较小。此外，当K为1时，两种跨模态映射函数的近邻保持能力仍最高，并且当K>1时迅速下降达到较低水平。

3.3 跨模态匹配验证

在IAPR TC-12和Wikipedia两个数据集上执行双向(图像到文本，记为I2T；图像到文本，记为T2I)匹配，其准确率-召回率曲线如图7～10所示。

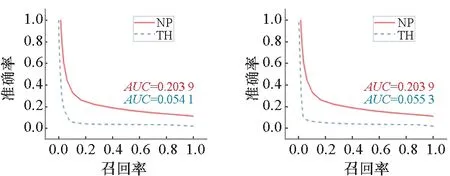
(a) Lin (b) Sigmoid

图7为IAPR TC-12数据集的图像-文本匹配结果，其中基于邻域传播的匹配方法在线性变换以及Sigmoid和TanH作为激活函数的深度神经网络中均取得了更高的准确率，而在以ReLU作为激活函数的神经网络中准确率较低，但仍然高于通过阈值直接匹配的方法。

(a) Lin (b) Sigmoid

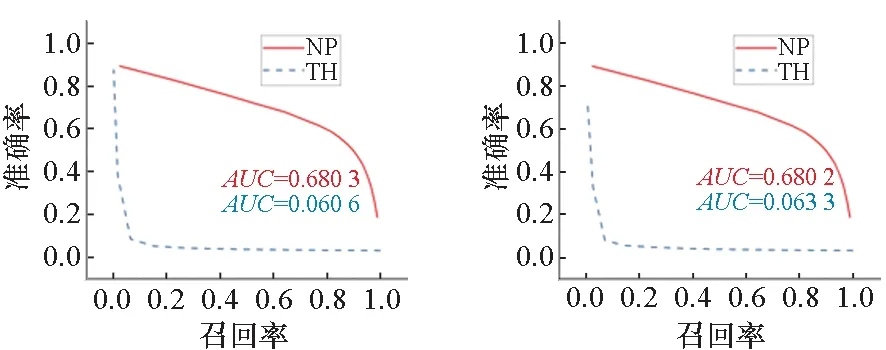
图8为IAPR TC-12数据集的文本-图像匹配结果，在线性变换和以TanH、Sigmoid为激活函数的深度神经网络中，基于邻域传播的匹配方法取得了更高的准确率，其AUC值远高于直接通过阈值进行匹配的方法；而在采用ReLU的深度神经网络中，两种匹配方法近似，其AUC值都较低。

(a) Lin (b) Sigmoid

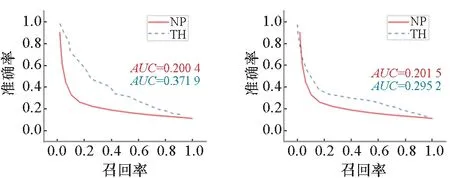
图9 为Wikipedia数据集图像-文本匹配结果，其中基于邻域传播的匹配方法表现不佳，在四种跨模态映射函数中其准确率始终低于基于阈值的匹配方法。

(a) Lin (b) Sigmoid

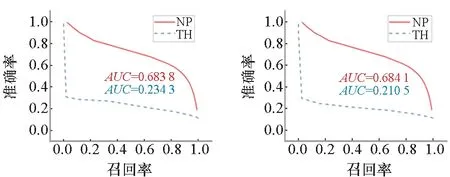
图10中，基于邻域传播的匹配方法在Wikipedia数据集文本-图像匹配任务中，准确性远远超过了基准方法。其AUC值高出基于阈值匹配的方法约0.45。

为验证基于邻域传播的匹配方法在部分情况下失效的原因，实验还通过计算样本与其近邻之间的距离，对数据集中文本和图像数据样本的近邻结构进行分析。其中，样本与其近邻的距离通过平均K近邻距离(mean K Nearest Neighbor Distance，mKNND)进行度量，其定义如下：

(11)

其中，NNj(xi)表示xi的第j近邻，d表示距离(实验中采用余弦距离)。

图11 (a)中，Wikipedia数据集图像数据的平均K近邻距离明显高于IAPRTC-12数据集，并且随着K的增大而增大。而在图11 (b)中，两个数据集的文本数据平均K近邻距离明显低于图像数据，其中Wikipedia数据集的平均K近邻距离更低并且随着K的增大增长较慢。根据图11的结果，可以推断图 9中基于邻域传播的匹配方法失效的原因之一是Wikipedia数据集的图像样本间差别较大，在邻域传播的过程中误差增大，导致匹配失效。此外，两个数据集上文本数据的近邻结构更加紧凑，这也是文本-图像匹配准确度高于图像-文本匹配的主要原因。

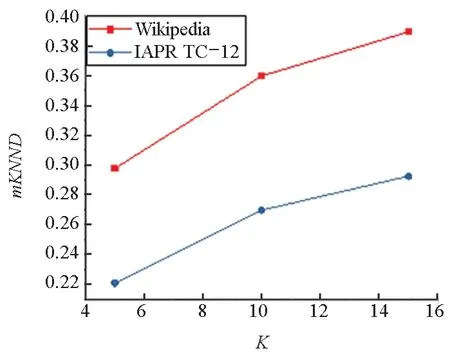
(a) 图像(a) Image

通过上述实验可以说明，尽管基于邻域传播的匹配方法在特殊情况下会失效，但是在大部分条件下都能有效地提升跨模态匹配的准确率，特别是当模态内和模态间近邻保持能力差别较大时。因此，本文提出的基于邻域传播的匹配方法对提升跨模态检索准确率具有重要意义。

4 结论

现有跨模态检索问题的研究中，通常通过深度神经网络或线性变换对不同模态的文本和图像数据进行跨模态映射，在此基础上进行相似度计算。而本文发现跨模态映射函数对近邻关系保持能力随着相似性判定的粒度增大而衰减，即存在“相似性漂移”问题。该问题导致误匹配的概率上升，进而降低检索的准确性。

为降低相似性漂移问题的影响，本文提出基于邻域传播的匹配方法，利用同模态近邻样本来发现待匹配对象的跨模态近邻。通过实验验证可以证明，该匹配方法对降低“相似性漂移”问题的影响，提高跨模态检索的准确率具有明显效果。尽管其有效性受到模态内近邻结构的影响，但是这不影响其具有重要参考意义。在未来的工作中，可以通过与普通的匹配方法结合来克服其局限性。例如设定一个阈值，当查询样本和其模态内近邻的距离小于阈值时采取邻域传播的匹配方法，当距离大于阈值时仍然通过该样本自身来进行匹配。