复合固体推进剂颗粒填充模型及其统计特性分析*

颜小婷，夏智勋，那旭东，沙本尚

(国防科技大学 空天科学学院, 湖南 长沙 410073)

固体火箭发动机具有成本低、结构简单、可靠性高等特点，在火箭和导弹中均有广泛应用。固体推进剂是固体火箭发动机的主要能量来源，其燃烧特性可显著影响固体火箭发动机的性能。固体推进剂的燃烧特性会同时受到外部燃烧环境和内部细观结构的影响，从细观角度研究各种因素对固体推进剂燃烧特性的影响，找出各种因素之间的制约关系，不仅可以掌握改善和提高推进剂燃烧性能的方法，还可以对推进剂配方的设计提供建议，大大降低推进剂配方研制的成本和危险。

当对体积足够大的复合固体推进剂进行空间平均分析时，推进剂的化学性质和物理性质均趋于一致。然而，从细观角度上来讲，复合固体推进剂中氧化剂颗粒和金属颗粒在基体中随机分布，会造成局部不均匀。推进剂宏观尺度上的燃烧特性和力学特性与推进剂成分组成、粒径分布以及细观尺度上的颗粒排列均密切相关，如燃烧速率、金属团聚或弹性模量等均在一定程度上由细观结构形态控制[1]。要分析细观结构对推进剂性质的影响，首先要对推进剂的细观结构有一个直观详细的认识。目前可采用的试验手段包括光学分析方法[2]、微型计算机电子扫描(microComputer Tomography, micro-CT)[3-5]和X射线断层摄影术(X-ray Computed Tomography, XCT)[6-7]等。由于试验方法耗时长、成本较高，且得到的推进剂细观结构不易直接用于后续计算分析，需要建立一个能够描述给定成分组成的推进剂异质细观结构颗粒填充模型，以此来预测推进剂特性。

利用数值算法生成颗粒填充模型的相关研究始于20世纪50年代，其所仿真的对象不仅限于固体推进剂，还包括沥青、混凝土、土壤等任意颗粒填充系统[8]，目前已成功实现三维填充模型的颗粒形状包括球体、椭球体、圆柱体以及各种多面体等[9]。表1对目前已有的部分颗粒填充模型进行了分类总结。复合固体推进剂填充体积分数较大且颗粒多采用多级配粒径分布，因此采用分子动力学方法更为普遍。Lubachevsky等首次提出了事件驱动的并行颗粒随机装填算法，也被称为LS算法[12]。之后又对算法进行了改进，使其可以用于二维圆盘颗粒和三维球状颗粒的随机装填[13]。由于LS适应性比较强，许多学者以其为基础发展了自己的颗粒填充模型[14-22]。本文所研究的对象为复合固体推进剂，因此采用的是事件驱动的分子动力学方法。本文工作是之后固体推进剂细观燃烧模型和铝团聚模型的基础。与颗粒粒径和颗粒质量分数相比，颗粒形状对推进剂燃烧性能的影响相对较小，因此模型中所有颗粒简化为球体。

表1 颗粒填充模型分类

利用颗粒填充模型得到的推进剂细观结构常用于后续对推进剂的燃烧性能或力学性能相关研究。然而，由于结构中颗粒数目大、计算量惊人，无法直接利用与实际试验所用尺寸相同的颗粒堆积体来进行数值计算。因此，研究者通常利用颗粒堆积体的代表体元(Representative Volume Element, RVE)来进行后续研究。此时，可以认为作为研究对象的复合材料的微结构为周期性结构，即为代表体元的重复性排列，代表体元必须可以在统计意义上代表整个颗粒堆积体，即与颗粒堆积体具有相同的统计相关函数值。显然，代表体元的尺寸越大，计算结果越准确，然而所需的计算成本也越高。因此，研究者必须要在保证计算精度的前提下找到尺寸最小的代表体元。

材料微观结构的统计相关函数的量化对于其结构、特性等相关研究非常重要，不同统计相关函数可以定义特定类别的无序材料的材料特性[23]，还可以用于计算异质推进剂的局部密度波动的固有长度，进而研究其对燃烧不稳定的影响[24]。Smith等对复合材料的统计特性进行了长期研究。起初的研究对象为由基体和单一半径颗粒组成的二维可穿透同心壳(Penetrable-Concentric-Shell，PCS)模型[25]，研究了颗粒不同渗透性下两点函数与两点距离和颗粒体积分数之间的关系。之后对单分散球体进行了拓展，针对“最近颗粒表面”建立了“最近表面分布函数”[26]。Hlushkou等[27]研究了三种不同粒径分布的颗粒填充结构的统计特性，计算得到多分散硬球随机填充结构的扩散系数。Lochmann等[28]研究了四种不同颗粒粒径分布的随机填充结构的统计特性，发现颗粒粒径分布对于结构的几何特性和统计特性具有较大影响。Kumar等[29]使用Rocpack生成了固体推进剂的微观结构，通过对一点和两点概率函数的计算描述了其统计形态，并引入增强模拟退火对周期单元内的颗粒位置进行了优化。Collins等[30]同样利用Rocpack生成固体推进剂微观结构并对其一点、两点和三点概率函数进行了研究，研究非线性过程时，更高阶统计可以对材料给出更精确的描述。

本文采用分子动力学方法，以硝酸酯增塑聚醚(Nitrate Ester Plasticized Polyether, NEPE)固体推进剂作为研究对象，生成了三维球状颗粒的随机填充结构体。利用Monte-Carlo方法对颗粒填充结构体的两点相关函数进行了计算，研究了细观特性对颗粒填充结构体的统计特性的影响。此外，基于得到的两点相关函数计算了不同颗粒相的最小RVE尺寸，进而得到了该NEPE固体推进剂的最小RVE尺寸，为后续NEPE固体推进剂细观燃烧模型相关研究提供基础。

1 复合固体推进剂颗粒填充几何模型

1.1 算法基本原理

NEPE推进剂由基体、氧化剂颗粒和金属颗粒构成，其中氧化剂颗粒和金属颗粒在基体中随机分布。在利用分子动力学生成推进剂颗粒填充模型过程中，首先将氧化剂颗粒和金属颗粒的中心随机分布在基体内建立初始构型，然后给定颗粒速度和粒径增长速度，其中粒径增长速度与颗粒粒径成正比。采用分子动力学算法计算基体内颗粒运动、颗粒间碰撞以及颗粒变大过程。随着颗粒粒径不断增大，颗粒体积分数不断上升，最后达到给定体积分数。颗粒粒径增大和颗粒运动会导致颗粒间碰撞的发生，从而使得颗粒位置不断调整，以避免出现颗粒重叠的情况。当颗粒体积分数到达给定体积分数时，计算停止，生成给定配方的推进剂颗粒填充模型。由此可见，分子动力学颗粒填充算法的核心问题是预测颗粒间的碰撞时间和碰撞后颗粒运动速度的改变量。所有颗粒被简化为球形颗粒进行处理。

由于颗粒在基体中随机分布，颗粒的初始位置和初始速度可以由随机数发生器随机给出。在初始时刻指定颗粒所占基体体积分数为1%，根据配方颗粒粒径分布来给定颗粒初始粒径。指定颗粒i的直径为di，粒径增长速度为ai，则t时刻该颗粒的粒径为di(t)=ait,(t>di0/ai)，颗粒状态变量为S(t)=(Ri(t),Vi(t))，其中Ri(t)和Vi(t)分别为颗粒i的颗粒中心位置和运动速度。根据分子动力学算法基本原理可以看出，颗粒初始状态对最终形成的推进剂颗粒填充模型的细观结构会有所影响，初始状态不同，最终形成的推进剂细观结构也不同，但是不会影响后续从宏观上对推进剂属性的分析和计算。

在从宏观角度研究推进剂特性时，可将整个复合材料视为代表性体积单元的周期性堆积。由于颗粒的运动与初始位置都是随机的，可能会出现颗粒越过RVE边界的情况，此时需要给出边界的颗粒施加周期性边界条件。对于D维问题，认为其周边有3D-1个计算域与其相邻，计算域边界设置为周期性边界，具有可穿透性，以此来确保填充模型体积分数的一致性和颗粒个数的恒定性。

1.2 NEPE推进剂颗粒填充几何模型构建

研究对象为NEPE推进剂，其主要成分粒径分布及质量分数如表2所示。其中黏合剂包括25%的聚乙二醇(PolyEthylene Glycol, PEG)和75%的塑化剂，塑化剂主要成分组成为50%的硝酸甘油(NitroGlycerin, NG)和50%的1,2,4-丁三醇三硝酸酯(ButaneTriol TriNitrate, BTTN)。

表2 NEPE推进剂主要成分粒径分布及质量分数

利用上文介绍的颗粒填充算法，根据所给配方和给定基体尺寸计算生成各颗粒的个数，计算得到NEPE推进剂的颗粒填充结构体。由于颗粒粒径之间差距较大，为了提高计算效率，生成两种不同边长的推进剂填充体用来分别计算不同粒径颗粒相的两点相关函数。实际生成的NEPE推进剂结构体边长分别为400 μm和1 000 μm，各相的颗粒个数和体积分数见表3。

表3 NEPE推进剂颗粒填充结构体颗粒组成及体积分数Tab.3 Composites and volume fraction of NEPE propellant pack

由于填充体中颗粒个数须为整数，无法保证不同边长填充体中各颗粒相体积分数完全相同，在此研究中近似认为生成的两填充体中同种颗粒相的体积分数相同。图1给出了构建的边长为400 μm的颗粒填充结构体的三维模型。其中，红色颗粒分别代表AP130和AP13，蓝色颗粒分别代表HMX86和HMX12，白色颗粒代表Al28。

图1 NEPE推进剂颗粒填充结构体Fig.1 Pack of NEPE propellant

图2 扫描电子显微镜下NEPE推进剂表面形态Fig.2 Surface morphology of NEPE propellant observed by the scanning electron microscope (SEM)

图2给出了在扫描电子显微镜下观察到的NEPE推进剂的表面形态，可以看出，颗粒随机分布在基体内且整体分布均匀，小颗粒可均匀分布于大颗粒之间，颗粒所占体积分数较高。这说明利用颗粒填充模型生成的颗粒填充体可以较好地体现出实际推进剂的细观结构。为了更准确直观地验证计算结果的准确性和可行性，在表4中将利用颗粒填充模型计算得到的颗粒体积分数与文献[5]中通过微计算机断层扫描技术重构丁羟推进剂细观结构得到的颗粒体积分数进行对比。对比结果显示，本文建立的细观填充模型与实际推进剂的颗粒体积分数误差较小，主要误差来自于细观填充模型无法考虑推进剂中可能存在的孔隙。

表4 丁羟推进剂二维断层图像[5]与细观填充体中各组分体积含量对比Tab.4 Comparison of the volume fraction of each component between the two-dimensional tomographic image of butyl hydroxide propellant [5] and the pack

2 复合固体推进剂细观结构统计特性分析

2.1 两点概率函数及其Monte-Carlo模拟

给定颗粒条件和颗粒堆积体的边长时，颗粒随机填充模型可以有多种实现方式，最终生成N种颗粒堆积构型，所有这些不同的颗粒随机堆积构型即构成样本总体Ω，每个构型均为该样本总体的成员，且空间为ω。从微观角度来看，样本总体中每个成员的微结构都与其他成员不同，但同时从宏观角度考虑则是相同的。宏观尺度是一种长度尺度，此时材料可被假设为具有平均量的连续结构。因此，可将整体均值定义为集合中所有成员上这些数量的期待值。即当样本总体中每个成员的概率和概率密度分别为P(ω)和p(ω)时，在填充模型中的x点处的函数F(x,ω)的总体均值可定义为：

(1)

此时为计算F(x,ω)的总体均值，需要计算每个成员的F(x,ω)值来求取平均值，计算量较大，因此可通过引入各态历经性来简化求值过程。

各态历经性的基本假设是样本总体中任一成员的所有状态都可应用于样本总体中的所有成员。由于从宏观尺度上来讲，颗粒填充模型生成的所有构型具有相同的物理性质和化学性质，因此可以认为样本总体Ω符合各态历经性假设，样本成员的体积为Vω。此时，可以通过研究单个样本成员的体积平均值来得到样本总体均值，即

(2)

由于在宏观尺度下材料可被视为具有周期性结构，因此可利用体积为V0的单个周期单元来计算样本总体均值，即

(3)

为描述多相颗粒填充模型的统计特性，首先要定义特征函数Iγ(x,ω)。

(4)

即当投点x落入γ相颗粒中时，特征函数取值为1，否则取值为0。

根据前文，其总体均值可由式(5)计算得到。

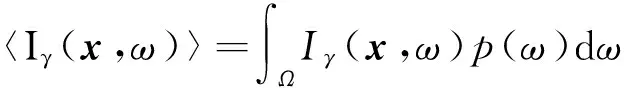
(5)

n点相关函数可以用来研究异质颗粒填充模型的微观结构的统计特性，其定义式可表示为：

(6)

即n点相关函数等于n个点x1，x2，…，xn随机投入空间时分别同时处于γ1，γ2，…，γn相的概率。通常来说，n点相关函数很难计算。研究对象仅为颗粒填充模型的几何参数即代表体单元的长度，不涉及颗粒间作用力对生成的推进剂的力学性质的影响，因此只需研究常用的一点相关函数和两点相关函数即可。

一点相关函数为最简单的多点概率统计，计算可得到生成推进剂颗粒填充模型中x点位于γ相的概率，其定义如下：

(7)

引入各态历经性，则一点相关函数可表示为：

(8)

式中，φγ为颗粒填充模型中γ相所占体积分数。

两点相关函数计算得到的是推进剂模型中两点x1，x2分别同时位于γ1相和γ2相的概率，其定义为：

(9)

根据两点相关函数的定义，在极端条件下两点相关函数满足以下取值式：

(10)

(11)

其中，δγ1,γ2为克罗内克符号(Kronecker symbol)，即

(12)

x12趋于0时，两点趋于一点。由于同一点不可能同时位于两个不同相内，因此γ1和γ2为不同相时，两点相关函数取值为零；γ1和γ2为相同相时，两点相关函数转变为一点概率函数问题。x12趋于无穷时，由于两点之间距离足够大，此时x1和x2具有统计独立性，两点相关函数取值为常数，与两点坐标及相对位置无关。

由于一点相关函数和两点相关函数较难直接计算，通常采用Monte-Carlo积分方法对其进行估算，即利用无穷和来近似积分。因此一点相关函数和两点相关函数可分别由式(13)、式(14)计算。

(13)

(14)

由上文可知，两点相关函数值会随两点之间距离增大最终收敛趋近于φγ1φγ2。本文目的在于得到最小周期单元体的尺寸，当随机选取两点x1和x2的两点相关函数值与φγ1φγ2足够接近时，可以认为尺寸不小于此时两点距离的推进剂颗粒填充模型与宏观推进剂在几何统计角度上具有相同特性。由于算法生成的推进剂颗粒填充模型具有各向同性，周期单元体的最小尺寸在各个方向具有相同值。因此，Monte-Carlo方法的实施主要通过在颗粒填充模型中多次置入距离为rd的两点来进行，通过计算不同rd下的两点概率函数来得到周期单元体的最小尺寸。

为了兼顾计算效率和计算精确性，采用介于投针方法和采样模板(Sampling Template, ST)方法之间的伪投针方法，即在颗粒填充模型中首先随机选取点x1作为球心，然后随机给出N2组天顶角θ和方位角φ，以rd作为半径在球面上随机选取N2个点作为x2，该过程重复进行N1次。对x1的取值施加边界限制，若x2位于颗粒填充体之外，则对其相应坐标施加周期性边界条件以保证计算结果的完整性。

2.2 NEPE推进剂细观结构统计特性及其RVE最小尺寸

根据上文可知，在极端条件下两点相关函数取值仅与两点所在两相的体积分数相关，为两相体积分数之积。因此可以将该值作为收敛值，随着两点距离增加，两点相关函数的值会逐渐趋近于该收敛值。当两点相关函数值与收敛值的误差始终小于5%时，认为其达到收敛值，此后两点之间距离继续增大对于两点相关函数的值不再有影响。达到收敛值时的两点之间距离则为对应颗粒相具有统计均匀性的微观结构的最小代表体元尺寸。所有颗粒相的最小代表体元尺寸的最大值即为该颗粒填充体的最小代表体元尺寸。

3 两点相关函数计算结果及影响因素分析

3.1 取样次数和球面取点数

研究对象为六相体，具有21个不同的两点相关函数，由于整体来说不同的两点概率函数具有相同的分布趋势，仅数值不同，因此这里只给出AP13-AP13的两点概率函数作比较。

图3给出了球面取点数N2均为100时不同N1下的两点相关函数，宏观来看曲线基本重合。图4给出了5次试验下两点相关函数的标准差，可以看出，标准差随N1的增大逐渐降低，当N1取50 000时，标准差基本比较稳定，并始终处于较低水平。

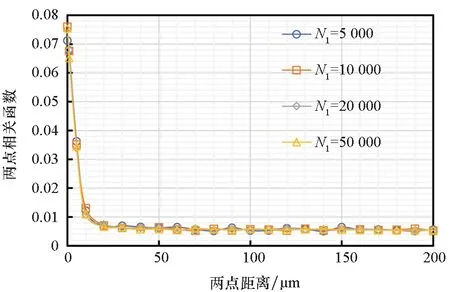
图3 N2为100时的两点相关函数Fig.3 Two-point correlation function when N2 is 100

图4 N2为100时两点相关函数的标准差Fig.4 Standard deviation of two-point correlation function when N2 is 100

图5和图6给出了取样次数为50 000时，不同N2下的两点相关函数及标准差，可发现此时N2对取值准确度的影响已基本可以忽略。N1取50 000时，无论N2如何取值，两点相关函数达到稳定值以后标准差始终低于0.000 5。因此，为同时保证计算精度和计算效率，在本文中取样次数N1和球面取点数N2分别取50 000和25。

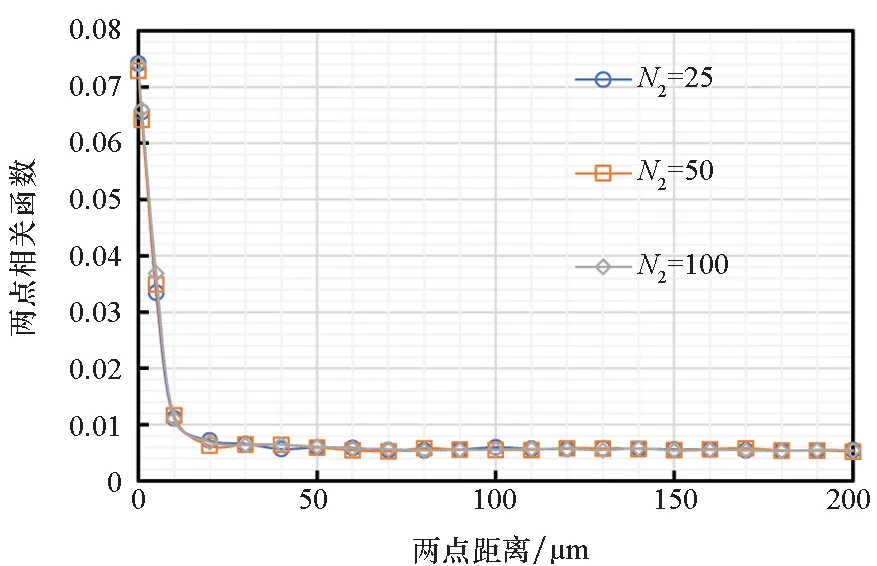
图5 N1为50 000时的两点相关函数Fig.5 Two-point correlation function when the N1 is 50 000

图6 N1为50 000时的两点相关函数的标准差Fig.6 Standard deviation of two-point correlation function when the N1 is 50 000

3.2 颗粒粒径

颗粒体积分数相同时，颗粒粒径越大，个数越少。图7和图8分别给出了HMX12和HMX86的两点相关函数和标准差随两点距离的变化情况，为提高计算效率，HMX12的两点相关函数利用边长为400 μm的填充体进行计算。

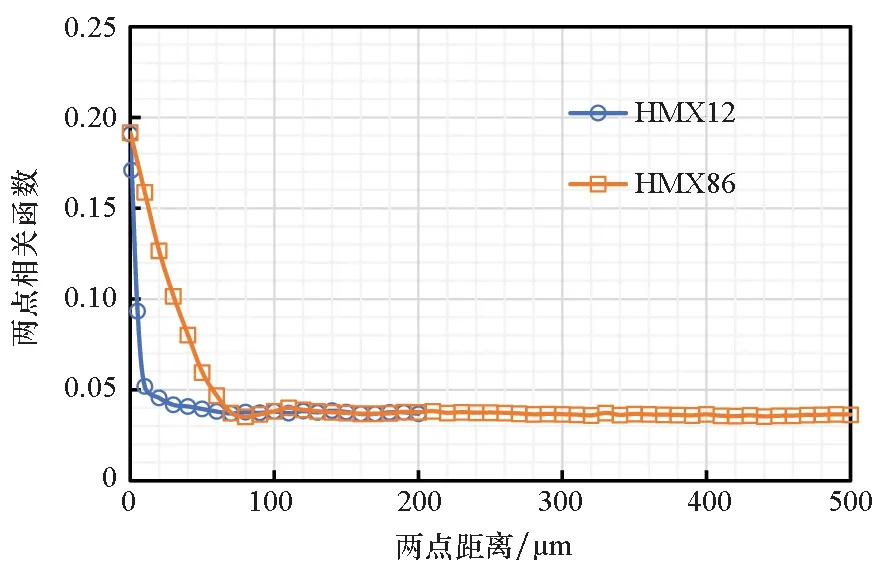
图7 HMX12和HMX86的两点相关函数与两点距离的关系Fig.7 Two-point correlation function as a function of rd of HMX12 and HMX86

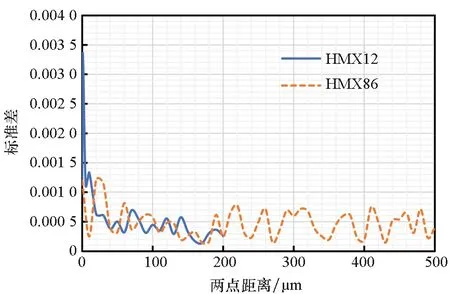
图8 HMX12和HMX86的两点相关函数的标准偏差与两点距离的关系Fig.8 Standard deviation of two-point correlation functions as a function of rd of HMX12 and HMX86

由图7～8可以发现，颗粒体积分数相同时，两种颗粒的两点相关函数收敛于相同值，粒径小的颗粒的两点相关函数达到收敛时所需两点之间的距离更小。由于两种颗粒个数不同，用变异系数(Coefficient of Variation, CV)来比较数据的离散程度。HMX12和HMX86的变异系数随两点距离的变化情况如图9所示，标准差和变异系数随两点距离与颗粒粒径比的变化情况分别如图10、图11所示。

图9 HMX12和HMX86的变异系数与两点距离的关系Fig.9 Coefficient of variation comparison of two-point correlation functions as a function of rd of HMX12 and HMX86

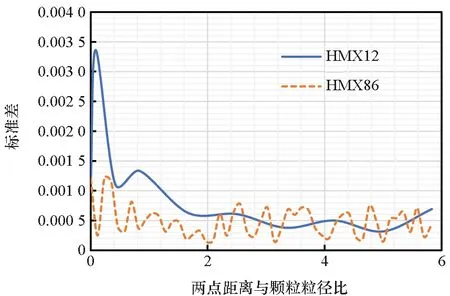
图10 HMX12和HMX86的两点相关函数的标准差与两点距离与颗粒粒径比的关系Fig.10 Standard deviation of two-point correlation functions as a function of rd/d of HMX12 and HMX86

图11 HMX12和HMX86的变异系数与两点距离与颗粒粒径比的关系Fig.11 Cofficient of variation comparison of two-point correlation functions as a function of rd/d of HMX12 and HMX86

N1和N2相同时，从图9可知HMX12的变异系数似乎低于HMX86。在图10和图11，以两点距离与颗粒粒径的比值作为横坐标，可发现在趋于收敛之后两种颗粒的标准差和变异系数均基本处于相同水平。因此可认为，两种颗粒体积分数相同时，其颗粒粒径对于N1和N2的选取没有什么影响。

图12给出了HMX12和HMX86的两点相关函数相对于收敛值的误差，可看出HMX12的两点相关函数更快达到收敛。为更直观地观察达到收敛值时两点之间的距离，选取局部图进行放大，如图13所示。通过观察和计算可得到在此推进剂填充模型中HMX12的代表体元尺寸为60 μm，HMX86的代表体元尺寸为300 μm。即体积分数相同时，粒径小的颗粒所需的RVE尺寸更小。

图12 HMX12和HMX86的两点相关函数关于收敛值的误差Fig.12 Error between two-point correlation function and convergence value of HMX12 and HMX86

图13 HMX12和HMX86两点相关函数关于收敛值误差的局部放大图Fig.13 Error comparison between two-point correlation functions of HMX12 and HMX86 and the convergence value within a certain range

3.3 颗粒体积分数

图14比较了AP13和HMX12的两点相关函数，可以发现在粒径相近时，两种颗粒收敛的速度近似相同，需要分别计算其最小RVE尺寸才能发现体积分数对其的影响。图15给出了AP13和HMX12的变异系数随两点距离的变化情况。从图15可发现，AP13的变异系数基本上均大于HMX12，说明当颗粒粒径相同时，其在颗粒填充体内所占体积分数越大，利用Monte-Carlo方法计算其两点相关函数时所需取点越少。

图14 AP13和HMX12的两点相关函数Fig.14 Two-point correlation functions of AP13 and HMX12

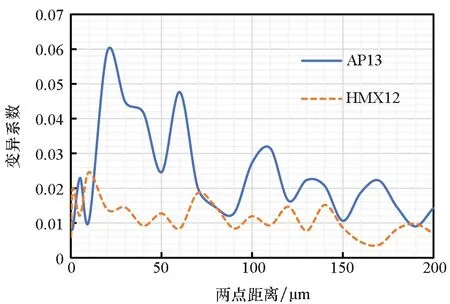
图15 AP13和HMX12的变异系数Fig.15 Coefficient of variation comparison of two-point correlation functions of AP13 and HMX12

图16给出了AP13和HMX12的两点相关函数值对于收敛值的误差，根据2.2节给出的RVE最小尺寸判断依据可看出，AP13和HMX12均可选取60 μm作为其代表体元尺寸，由于AP13和HMX12的粒径较小，这种结果可能是由取点不够密集造成。因此，在两点距离50～70 μm之间重新密集取点计算两点相关函数及其相对于收敛值的误差，进而计算AP13和HMX12的代表体元尺寸。图17为图16的局部放大图。根据RVE最小尺寸判断依据，由图17可得，HMX12在两点距离为54 μm时达到收敛，AP13在两点距离为60 μm时达到收敛，且AP13相对于收敛值的误差波动更大。说明颗粒粒径相近时，体积分数越大，其代表体元长度越小。

图16 AP13和HMX12的两点相关函数关于收敛值的误差Fig.16 Error comparison between two-point correlation functions of AP13 and HMX12 and the convergence value

图17 AP13和HMX12的两点相关函数关于收敛值误差的局部放大图Fig.17 Error comparison between two-point correlation functions of AP13 and HMX12 and the convergence value within a certain range

3.4 不同颗粒粒径分布

图18给出了两种颗粒相的三个两点相关函数的分布，图19比较了这三个两点相关函数的变异系数。可以发现，AP130-AP130的变异系数最大且波动较大，HMX86-HMX86的变异系数始终处于较低水平且相对平缓，AP130-HMX86的变异系数基本处于二者之间。

图18 AP130-AP130，HMX86-HMX86和AP130-HMX86的两点相关函数Fig.18 Two-point correlation functions of AP130-AP130, HMX86-HMX86 and AP130-HMX86

图19 AP130-AP130，HMX86-HMX86和AP130-HMX86的变异系数Fig.19 Coefficient of variation comparison of two-point correlation functions of AP130-AP130, AP130-HMX86 and AP130-HMX86

图20给出了这两种颗粒相的三个两点相关函数关于收敛值的误差。可发现，在给定两点长度内，两点相关函数已达到较好收敛效果。为了更清晰地比较不同两点相关函数收敛速度及其最小代表体元尺寸，图21通过对数据范围进行筛选对图20进行了放大。根据RVE最小尺寸判断依据可得出AP130-AP130的最小代表体元尺寸为750 μm，HMX86-HMX86的最小代表体元尺寸为130 μm，AP130-HMX86的最小代表体元尺寸为120 μm。由此可推，对于多级配模型，不同颗粒相的两点相关函数比单颗粒相的两点相关函数收敛更快，其最小代表体元尺寸比两种单颗粒相的最小代表体元尺寸小。

图20 AP130-AP130，HMX86-HMX86和AP130-HMX86的两点相关函数关于收敛值的误差Fig.20 Error between two-point correlation functions of AP130-AP130, HMX86-HMX86 and AP130-HMX86 and the convergence value

图21 AP130-AP130，HMX86-HMX86和AP130-HMX86的两点相关函数关于收敛值误差的局部放大图Fig.21 Error comparison between two-point correlation functions of AP130-AP130, HMX86-HMX86 and AP130-HMX86 and the convergence value within a certain rangee

4 结论

本文利用基于分子动力学的复合固体推进剂颗粒填充模型，以NEPE固体推进剂为研究对象，生成了指定成分的NEPE推进剂的颗粒填充体。为了得到颗粒填充体的最小代表体元尺寸，为之后对于推进剂燃烧特性的研究提供模型基础，基于Monte-Carlo理论，采用伪投针方法对颗粒填充体的统计特性进行了研究。研究发现：

1)两种颗粒体积分数相同时，其颗粒粒径对于投点次数的选取几乎没有影响，但是对最小代表体元尺寸有较大影响。体积分数相同时，最小代表体元尺寸与颗粒相直径具有直接关系，直径越大，实现统计均匀性所需的两点距离越大。

2)当颗粒粒径固定时，其在颗粒填充体内所占体积分数越大，利用Monte-Carlo方法计算其两点相关函数时所需取点的次数越少。当颗粒相直径相近时，颗粒在填充体中体积分数越大，实现统计均匀性所需的两点距离越小，即其最小代表体元尺寸也越小。

3)对于多级配粒径分布模型，分别位于不同颗粒相的两点相关函数比对应的两种单颗粒相的两点相关函数收敛更快，即多级配颗粒的最小代表体元尺寸要小于对应单颗粒的最小代表体元尺寸。为保证计算精度，颗粒填充体的最小代表体元尺寸应不小于填充体内所有颗粒相的最小代表体元尺寸中的最大值。因此，在实际应用中，可考虑只计算单颗粒相的最小代表体元尺寸，其中的最大值即可用作该颗粒填充体的最小代表体元尺寸。