动态威胁环境下单无人机测向定位航迹优化算法*

陈方正，郝绍杰

(中国电子科技集团公司第四十一研究所， 山东 青岛 266555)

随着无人机(Unmanned Aerial Vehicles，UAV)技术的发展，将UAV平台作为机动观测站，搭载测向设备对敌方目标进行探测定位越发受到重视。单站测向定位是指利用运动的单个观测站在不同位置测得的目标方位角信息[1]，结合某种估计算法实现对目标的快速定位和跟踪。测向手段既可以是传统意义上的无线电测向，也可以是利用光电设备的测向[2]。利用UAV等单观测站进行测向定位航迹优化问题的本质是研究如何通过优化观测平台的运动轨迹来提升对目标预测的可观测性问题。目前比较有代表性的方法包括，基于Fisher信息矩阵(Fisher Information Matrix, FIM)及其变形形式的最优航迹规划算法[3-6]，以方位角度变化率最大为目标的航迹优化算法[7]，以定位误差几何因子(Geometrical Dilution Of Precision，GDOP)最小化为目标的最优定位航迹优化算法[8]，以滤波协方差最小为准则的航迹优化算法[9]，以及将上述多种目标函数结合的航迹优化算法[10]等。

然而这些研究大多基于理想空间条件下，即未考虑UAV等单观测站定位航迹受威胁和障碍等约束条件的影响，限制了单站测向定位的实际应用，因此近年来结合复杂的飞行环境，进行测向定位航迹优化成为研究的热点。He等[11]研究了在威胁障碍环境下机动单站对静止和机动目标定位的最优机动策略。吴昊等[12]考虑多种战场威胁约束，通过打分函数引导路径选择，得到在约束条件下的UAV最优定位航迹。由于定位问题的特殊性，事先并不能知道目标的确切位置，因此需要UAV等单观测站边定位边规划。然而以往关于单站测向定位航迹优化的研究都是基于静态环境下的单步最优原则。在动态战场环境下，单步最优原则使得UAV的预判信息极为有限，可能导致UAV由于机动能力不足而与障碍发生碰撞。

因此本文以单架UAV作为测向定位平台，针对动态战场环境下的测向定位问题，基于动态窗口法(Dynamic Window Approach，DWA)思想，提出多步预测求解最优航迹的算法，在线生成满足UAV运动学约束的航迹，解决单架UAV在动态战场环境下的测向定位航迹优化问题。

1 问题描述

1.1 测向定位的问题描述

考虑到进行测向定位时目标与UAV之间的高度差异远小于水平方向的距离，因此将UAV测向定位简化为二维平面中的定位问题，如图1所示。其中：oxy为地面惯性坐标系；XT为待定位目标，其坐标为[xT,yT]T；XU,k代表UAV，k为时间步，Vk为其速度矢量，ηk为其观测的目标的方位角。UAV离散形式运动学模型可写为：

XU,k+1=AXU,k+BUk

(1)

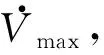
(2)

其中，Δt为状态变化时间间隔。

对于测向定位问题，假设目标静止，不考虑过程噪声，选取XT为待估计的状态变量，则目标离散状态方程可写为：

XT,k+1|k=Φk+1|kXT,k|k

(3)

其中

(4)

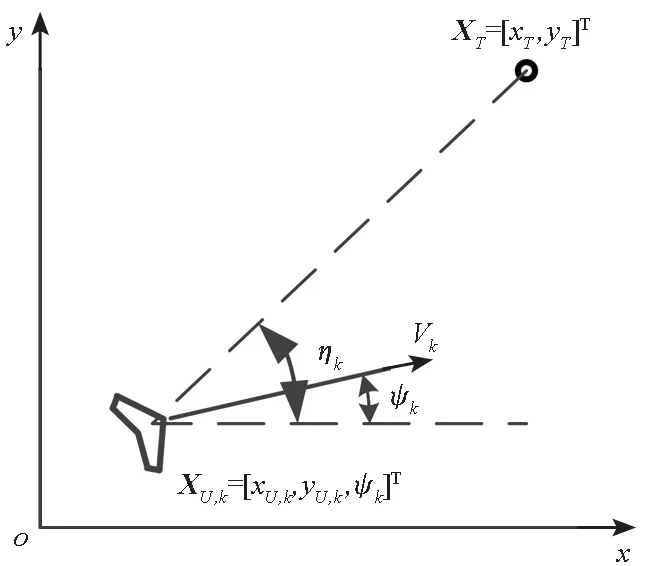
图1 测向定位示意图Fig.1 Illustration for bearing-only target localization

由图1可知，UAV对目标的方位观测方程可表示为：

(5)

式中，εk是均值为0，方差为σ2的高斯白噪声序列。

1.2 测向定位在动态战场环境下面临的问题

典型战场环境包括：敌方雷达探测威胁、火力威胁、地形威胁、建筑等障碍物威胁以及危险天气威胁等各种威胁因素。以往关于定位航迹优化的研究中都是针对静态环境[11-12]，即威胁因素状态固定，这与实际差异较大。本文中将威胁因素归纳为雷达探测威胁和障碍物威胁，研究在动态战场环境下雷达突然开关机和障碍物机动时UAV的最优测向定位航迹。

1.2.1 敌方雷达探测威胁

被敌方雷达捕获会使UAV处于危险之中。雷达能否探测到UAV与其反射信号的信噪比有直接影响。根据文献[12]对于确定的目标和雷达，其信噪比SN可表示为：

(6)

式中，下标i表示雷达编号，di为雷达与UAV之间的距离，dmax,i为雷达最大探测距离，bi为常数。UAV飞行过程中应当尽量避免被雷达探测到。动态战场环境下，探测雷达可能突然开机，而若此时UAV正好处于雷达探测范围中，UAV飞行航迹应能使SN尽快降低。

1.2.2 障碍躲避

UAV处于火力威胁、地形威胁、建筑等障碍物威胁以及危险天气威胁之中时将会导致其坠毁，因此可以将上述威胁均等效为障碍物，UAV不能与其碰撞。障碍物既可以是固定的，也可以是不断运动的。在二维环境下，本文将不同障碍物均等效为不同直径的圆形固定障碍或者可动障碍，UAV在飞行过程中时刻需要对这些障碍进行躲避，避免与障碍物相撞，即满足：

obj,k=Rj,k-rj>0

(7)

式中，j为障碍物编号，Rj,k为UAV与障碍物中心的距离，rj为障碍物半径，obj,k为UAV与障碍物边缘的距离。

2 基于DWA的多步预测方法

在以往关于单站测向定位航迹优化的研究中多是基于单步最优机动策略。如图2所示，即根据观测站的机动能力和单位时间运动距离，在可行航向区间内离散若干航点，根据定位最优准则，从这些航点中选择最有利于快速定位的航向。然而这种方法在障碍环境中预判信息极为有限，不能充分利用观测站的机动性提前躲避障碍，可能会导致UAV因机动能力不足而与障碍碰撞。

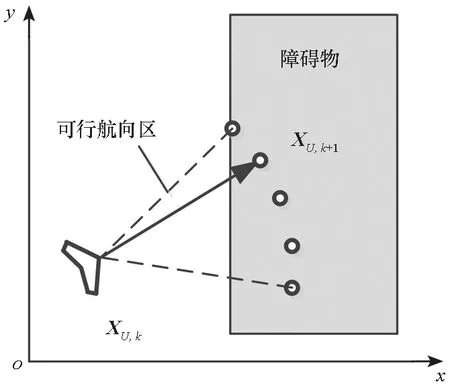
图2 单步最优机动策略示意图Fig 2 Illustration for one-step optimal maneuver strategy

DWA算法的主要思想是在速度空间中选择不同的线速度和角速度组合作为控制量，基于UAV运动学模型，计算在模拟预测时间内可能的飞行航迹集合，通过对这些航迹进行评价，选择最优航迹的控制量作为下一步的控制目标。DWA因实时性强和直接考虑机器人运动学约束等特性而被广泛应用于动态复杂环境下的机器人的障碍威胁规避[13]。DWA可以有效增加测向UAV的预判信息，解决复杂障碍环境下的UAV避碰和定位问题。

本文以FIM行列式最大作为UAV测向定位航迹优化的准则，以提高对目标的定位精度。基于DWA多步预测的思想，需要解决对预测航迹的评价问题。文献[14]推导了无过程噪声条件下FIM的递推计算方法：

(8)

式中，FIMk为Fisher信息矩阵，Rk为观测噪声序列εk的协方差矩阵，Hk为观测方程h(·) 的雅可比矩阵，表达式为：

(9)

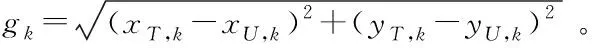
JFIM=det(FIMk+n)

(10)

敌方雷达威胁评价函数由式(11)计算，为UAV在整条预测航迹上被q个雷达探测的SN值之和。该评价函数使UAV更倾向于选择不容易被发现的航迹，若UAV不在雷达探测范围内，则航迹不受影响。

(11)

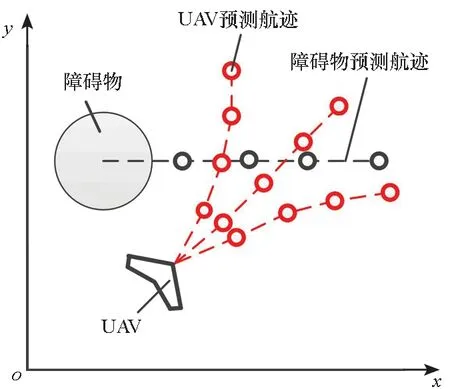
图3 预测碰撞时间计算示意图Fig.3 Calculation of predicted collision time

障碍躲避采用与碰撞时间相关的评价函数[15]。如图3所示，假设UAV可以通过自身传感器估计障碍物的运动速度和方向[16]，则可以对其运动航迹进行预测，基于UAV和障碍物每一时刻的位置，通过式(7)可以判断两者发生碰撞的时间。对于UAV附近的多个障碍物，需依次进行判断，并选择最小碰撞时间作为该条预测航迹的避碰评价函数JT。在所有的预测航迹中，选择预计碰撞时间最晚的航迹有利于UAV躲避障碍，因此以JT最大为避碰准则。

综合考虑定位、雷达威胁和避碰因素，一条航迹的总评价函数为：

Jp=c1JFIM,p+c2JSN,p+c3JT,p

(12)

式中，c1=0.2，c2=0.3，c3=0.5为权重因子，p为预测航迹数。考虑到无人机避障和躲避雷达威胁是其生存进而完成定位任务的前提，因此无人机避障和雷达躲避的评价指标权重系数较大。多条航迹构成目标函数集合，则

J=[J1,J2,…,Jp]T

(13)

3 基于DWA的单UAV测向定位航迹优化算法

基于DWA的单UAV测向定位航迹优化算法如算法1所示，其中P为扩展卡尔曼滤波(Extended Kalman Filter， EKF)过程中的估计误差方差矩阵。

算法1 基于DWA的单UAV测向定位航迹优化算法

算法1中，第2～12步通过基于DWA的UAV航迹优化算法形成下一步控制指令。由于该控制指令是由对最优航迹的评价得到的，因此包含了多步预判的信息。第13步UAV根据控制指令机动。第14步UAV基于新的测向值，使用EKF进行目标状态估计；第15步UAV更新FIM。如此反复迭代直至UAV定位误差收敛。

4 仿真实验

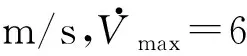
4.1 无障碍条件下定位航迹对比

首先考察定位目标函数的有效性，飞行环境中不考虑障碍物和雷达威胁，此时JSN为0，JT为固定常数，UAV航迹优化目标函数仅与JFIM有关。分析预测步数不同对航迹形状和定位误差收敛过程的影响，并与一般匀速直线航迹进行比较。每种条件进行50次Monte-Carlo仿真，每次测量平均定位误差均方差(Root Mean Square Error, RMSE)为：

(14)

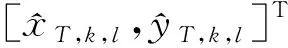
表1 不同航迹最终定位结果

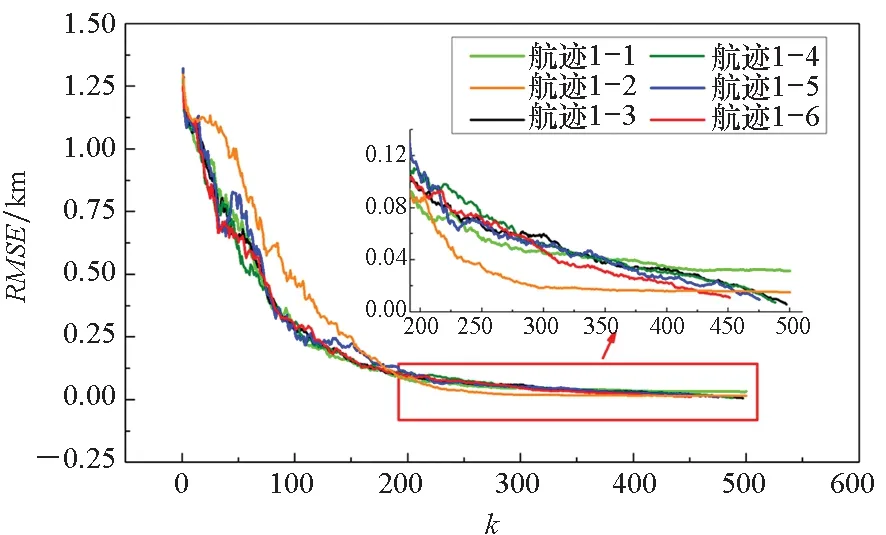
图4 平均定位误差收敛曲线Fig 4 Convergence curve for RMSE

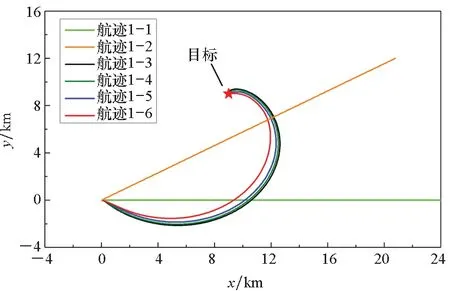
图5 不同航迹对比Fig.5 Comparison of different trajectories

结合表1和图4可知，当k≤200时，航迹1-1比航迹1-2 RMSE收敛速度快，但是最终定位精度却最低。而优化航迹1-3～1-6不但前期RMSE收敛速度快，并且能够达到更高的定位精度，这说明评价函数JFIM对于提升UAV测向定位精度是有效的。图4中，当k≥300时，n值越大，RMSE收敛加快，这说明增加预测步数n有利于进一步改善UAV的定位收敛过程。

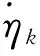
4.2 动态复杂障碍条件下航迹对比

在仿真环境中引入障碍和雷达干扰，其中两个固定障碍半径均为r1=r2=1 km，位置分别为Xob,1=[2 km,2 km]T，Xob,2=[12 km,4 km]T，运动障碍半径为r3=1 km，初始位置为Xob,3=[8 km,2 km]T，沿x轴做速度为Vob=12 m/s的匀速直线运动，雷达位置为Xradar=[6 km,2 km]T，最大探测半径为dmax,1=4 km。其他仿真条件不变，每种条件同样进行50次Monte-Carlo仿真，结果如表2所示，其中航迹2-2～2-4均达到收敛表1中相同的收敛精度，说明动态环境的引入没有影响最终的定位性能。而航迹2-1由于与障碍发生碰撞未完成定位任务，因此无最终定位精度。

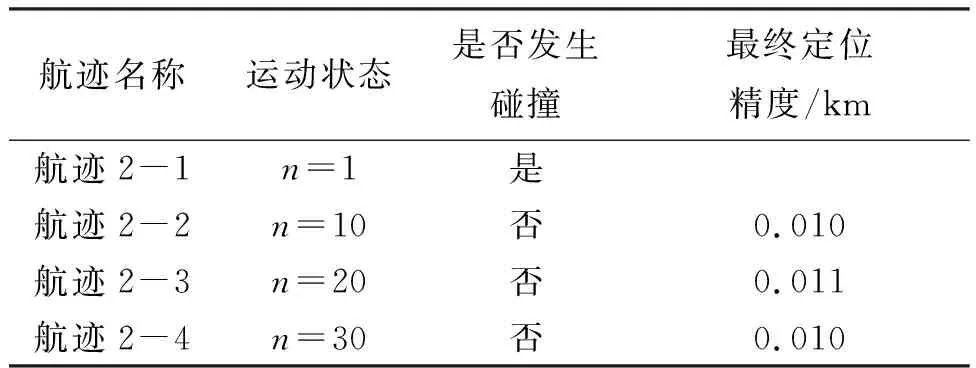
表2 不同航迹定位结果

不同时刻航迹如图6所示。当k=150 时，各条航迹如图6(a)所示。此时雷达未开机，不会对UAV航迹产生影响。对于航迹2-1，n=1为单步最优原则。当UAV预测到将与障碍物碰撞时，由于其机动能力有限，无法产生有效规避，从而导致其最终与障碍物发生碰撞。对于航迹2-2～2-4，均未与固定障碍1发生碰撞，并且n越大，预知信息越多，航迹越平滑。当k=290时，各条航迹如图6(b)所示。雷达突然开机时，UAV均在雷达探测范围内，此时UAV迅速转向逃离雷达探测边界，从而减小被雷达探测到的概率。在k=290～330范围内，航迹2-2～2-4依次与运动障碍相遇，由于UAV能够对障碍物运动进行预判，因此3条航迹均能成功避开运动障碍物，整个运动过程未发生碰撞，如图6(b)～(d)所示。

当定位结束时，如图6(e)所示，各条航迹均收敛到目标附近，定位过程结束。比较航迹2-2～2-4发现，n值越大，UAV控制信息中包含的预测信息越多，航迹越平滑。

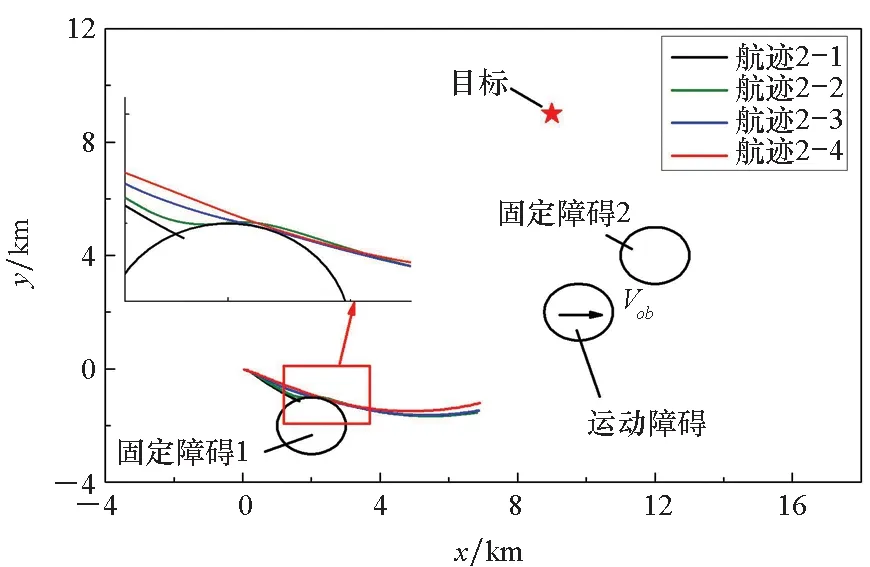
(a) k=150时刻航迹(a) Trajectories at k=150

(b) k=290时刻航迹(b) Trajectories at k=290

仿真结果表明，本文提出的算法能够在雷达探测威胁和动态障碍环境的影响下依然保证较高的测向定位精度，实现了UAV在动态战场环境下对目标的测向定位航迹优化。

5 结论

本文基于DWA多步预测的思想，提出了一种应用于动态战场环境下的单站测向定位航迹优化算法。该方法将测向定位目标函数由单步最优原则扩展到对多步预测航迹的评价，同时考虑对雷达探测威胁和运动障碍的躲避，在线生成满足UAV运动学约束的航迹。仿真结果表明，增加预测步数，一方面有助于提升测向定位的收敛速度，另一方面由于增加了UAV对障碍的预判信息，使其更早地对障碍物(包括运动障碍)进行规避。航迹优化算法使UAV在复杂动态环境的影响下依然能够完成高精度测向定位任务。