数值模拟气液针栓式火箭发动机喷雾燃烧对声学激励的响应*
2021-10-10沈赤兵杨林涛
金 烜,沈赤兵,林 森,杨林涛
(1. 国防科技大学 空天科学学院 高超声速冲压发动机技术重点实验室, 湖南 长沙 410073; 2. 西安卫星测控中心, 陕西 西安 710043)
高频燃烧不稳定是液体火箭发动机研制过程中极具挑战性的课题[1]。发生高频燃烧不稳定时,燃烧室壁面热流增大导致发动机在几分之一秒内被烧毁,高幅值的压力振荡甚至会引起发动机瞬间爆炸。目前,关于高频燃烧不稳定性的维持机理尚未达成共识,预测燃烧稳定性依然是新型发动机研制过程中最困难的一环[2],一个原因就是喷注器采用不同的推进剂组合,引起雾化、蒸发、混合与燃烧等过程发生变化。工程上往往采用大量全尺寸试车来克服高频燃烧不稳定,但试错法的燃烧试验成本和迭代设计成本高昂,因此能在发动机预研阶段采用理论分析、数值仿真和试验验证等多种手段来探索不稳定机理有着巨大的经济价值和时间效益。
国内外对液体火箭发动机非线性不稳定燃烧机理[3-5]和各类抑制装置[6-8]已开展了系统的研究。同时随着推进剂无毒化逐渐成为未来的主流,常规的同轴式喷注器和撞击式喷注器分别采用液氧/液氢等低温推进剂组合与液氧/煤油等常温推进剂组合,已开展大量燃烧稳定性研究并广泛应用于新型运载火箭[3, 9-10]。
起源于20世纪50年代的针栓式喷注器具有结构简单、面积可调和燃烧稳定等诸多优点[11],若采用液氧/甲烷双组元推进剂,可在未来星际探索中实现飞行器就地加注和重复使用[12]。针栓式发动机燃烧特性关于几何尺寸和喷注条件的参数化研究已见诸报道[13-17],但其中关于其声学振荡特性的研究还较少,且局限于燃烧室压力采集及其频谱分析、非稳态喷雾燃烧的光学观测及其模态分解等分析手段。
相比于试验和非线性理论分析,数值模拟振荡燃烧可获取更详细的流场信息。前期的仿真工作[15]说明LOX/GCH4针栓式发动机工作时燃烧稳定性较好,燃烧室压力以低频小幅振荡为主。本文在此基础上借鉴文献[9-10]中旋转齿轮声学扰动装置的思路,通过对燃烧流场施加速度扰动来产生横向声学振荡响应,以期在热试之前预先了解声学激励频率对非稳态喷雾燃烧的影响。
1 数值物理模型
1.1 物理模型
LOX/GCH4针栓式火箭发动机样机采用设计流量为356 g/s的液氧中心式气液针栓喷嘴(液氧和气甲烷的设计流量分别为257 g/s和99 g/s)。如图1(a)和图1(b)所示,液氧通过针栓中心流道后自针栓头端的一系列孔呈放射状径向喷出,气甲烷从喷注器集气腔流经针栓外侧的环缝轴向喷出形成气膜,径向射流与轴向气膜呈90°交叉撞击后推进剂发生雾化、混合与燃烧,局部动量比为1,相关结构参数如下:Ls=12 mm,Dp=12 mm,h=0.66 mm,d=0.84 mm,N=12。数值模拟采用的计算域见图1(c),全文坐标原点取燃烧室入口横截面的中心点,流动方向为x,宽度方向为z,高度方向为y;本文通过矩形燃烧室方案实现用横向振荡模拟圆筒形燃烧室内可能出现的复杂切向振荡,同时矩形燃烧室方案有利于在壁面局部位置开设观察窗,便于热试过程中同步观测喷雾分布和火焰形态(开窗观测手段已在针栓式液体火箭发动机中多次应用[5, 13-14]);矩形燃烧室内部空间宽45 mm,高141 mm,长348 mm,喷管喉部处高收缩至8.2 mm,喷管出口处高扩展至11.9 mm;数值计算时还在z=0平面上设置多个压力监测点,其中P4和P7位于燃烧室轴线,其余位于壁面,各点对应的x轴坐标如下:-28 mm(P01/P02), 0(P1/P2), 174 mm(P3/P4/P5), 174 mm(P6/P7/P8)。

(a) 针栓式发动机结构示意图(a) Schematic of pintle engine
1.2 计算方法和网格划分
LOX/GCH4针栓式火箭发动机的两相喷雾燃烧流动采用Euler-Lagrange方法开展计算,控制方程包含Euler坐标系下的雷诺平均纳维-斯托克斯(Reynolds Averaged Navier-Stokes,RANS)方程(气相)和Lagrange坐标系下的离散颗粒轨道方程(液滴),两相之间的耦合通过气液相互作用源项实现。采用有限体积法离散控制方程,而后采用密度基隐式算法进行求解。考虑到计算资源有限,计算中采用Jones-Lindstedt四步反应机理结合涡耗散概念模型对GOX/GCH4化学反应过程进行模拟[18]。
计算域构型(见图1(c))中GCH4的入口边界给定质量流量和温度(300 K);液氧喷注采用离散相模型(Discrete Phase Model, DPM),以针栓头端的液氧喷孔面(见图1(b))作为入口喷射源,颗粒类型为Droplet,所有液滴的喷注方向垂直于喷孔面,并设置液滴的质量流量、入口温度(80 K)、入口速度(33.48 m/s,对应喷注压降为1 MPa)和液滴粒径(10 μm);出口边界由数值计算外推给定。所有壁面边界采用绝热非滑移壁面条件,液滴与壁面发生碰撞后发生球形反弹。特别说明的是,液滴粒径的选择是基于前期的仿真研究[15],燃烧室压力振荡幅度随着液滴粒径增大而上升,当液滴粒径大于60 μm时出现低频不稳定燃烧,进一步增至110 μm以上则发生熄火。为避免低频不稳定燃烧对声学振荡的影响和发动机性能下降,此处液滴粒径取10 μm。
由于计算域构型结构不规则,喷注器集气腔和环缝部分采用结构网格,燃烧室和喷管部分采用非结构网格,两部分在环缝出口面进行拼接。其中,非结构网格部分采用自下而上的方法生成:先在不同边界处生成密度不同的面网格,在此基础上于针栓头端表面生成的边界层网格,最后在其余空间里充填局部加密的体网格,从而保证混合反应区和尾喷管有相对较密的网格。整个计算域包含74万个网格单元,满足标准k-ε湍流模型和壁面函数的使用要求,时间步长取5×10-6s。
关于计算方法及其验证和网格无关性的详细介绍参见文献[15],同时文献[5]通过对比封闭方腔内的一维声学振荡理论解和二维仿真结果,证明了本文的计算方法适合于声学振荡数值模拟。
1.3 声学激励方法
本文的计算顺序是先按前文设置计算至稳定燃烧阶段(作为无激励工况进行对照),而后以此结果为初始状态并开启声学激励继续仿真。根据2.1节无激励设计工况下矩形燃烧室构型的计算结果可知,燃烧室内的混合比O/F分布极不均匀,主反应区和高温燃气大部分聚集在燃烧室前半段,而声学激励的存在将进一步促进甲烷与氧气之间的反应,因此本文选取燃烧室前半段施加如图2所示的在y方向上的速度扰动(见式(1)),其产生的影响相比于选取燃烧室后半段将更明显。数值计算中通过加载自定义函数(User Defined Function, UDF)将动量源项Mom′(即网格单元内的动量变化率,见式(2))导入动量守恒方程来实现。

图2 横向速度扰动设置Fig.2 Setup of transverse velocity disturbance

(1)
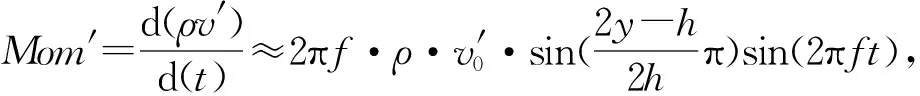
(2)
其中,v′0为扰动幅值(60 m/s),h为燃烧室高度(141 mm),f为扰动频率,ρ为气体密度。本文重点研究相同扰动幅值下喷雾燃烧对不同扰动频率(3 000 Hz、4 538 Hz和6 000 Hz)的动态响应,其中4 538 Hz是该燃烧室的一阶横向(1T)振荡模态固有频率(fc=c/(2h),c为热力计算得到的相应燃烧室声速(1 280 m/s))。
2 计算结果及讨论
2.1 无激励工况
由于目前对LOX/GCH4针栓式发动机的燃烧流场缺乏了解,本节首先采用开窗热试观测结果对仿真计算进行验证。无激励验证工况的喷注器环缝宽度h和喷孔直径d分别为2.23 mm和0.56 mm,对应GCH4和LOX的流量分别为37.2 g/s和84.5 g/s,其余发动机结构参数及仿真设置与本文1.1节一致,开窗热试采用文献[14]提出的单相机方案对喷雾(背景光成像)和火焰(自发辐射成像)同步观测。稳定燃烧阶段喷嘴附近的喷雾轨迹和火焰形态如图3所示,对比表明:①仿真得到的液氧液滴分布区域与热试结果相近,均在针栓头附近完成了快速蒸发,而观察窗范围内均以喷雾外缘区域燃烧最为剧烈,验证了计算方法和网格的合理性;②热试结果显示液氧射流的喷雾锥角更大且射流表面存在表面波结构,原因在于仿真采用RANS方法和DPM分别模拟湍流流动和液氧射流,前者无法精确模拟连续相流场中的小尺度涡结构,后者忽略了液氧射流的破碎雾化过程(假设液氧在喷孔出口已雾化成离散液滴),故无法反映真实的气液雾化过程;③自发辐射成像得到的火焰分布范围比仿真结果更广,原因除了喷雾锥角的差异外,还在于试验拍摄得到的图像是沿视图方向的积分,所有液氧射流蒸发燃烧都会在图像上产生叠加作用,另外观察窗玻璃边缘位置的烧蚀现象也对图像产生了干扰(如图3所示红色虚线框),而仿真结果给出的仅是燃烧室对称面上的归一化释热率,主要体现上下两股液氧射流的燃烧反应,轴线附近没有明显的火焰;④热试图像中火焰附着在液氧喷孔位置,而仿真得到的燃烧火焰距液氧喷孔有一段距离,原因在于仿真过程中燃烧反应的快慢由气相组元的混合速率决定,液氧离开喷孔后要经历蒸发与混合后才能参与燃烧。
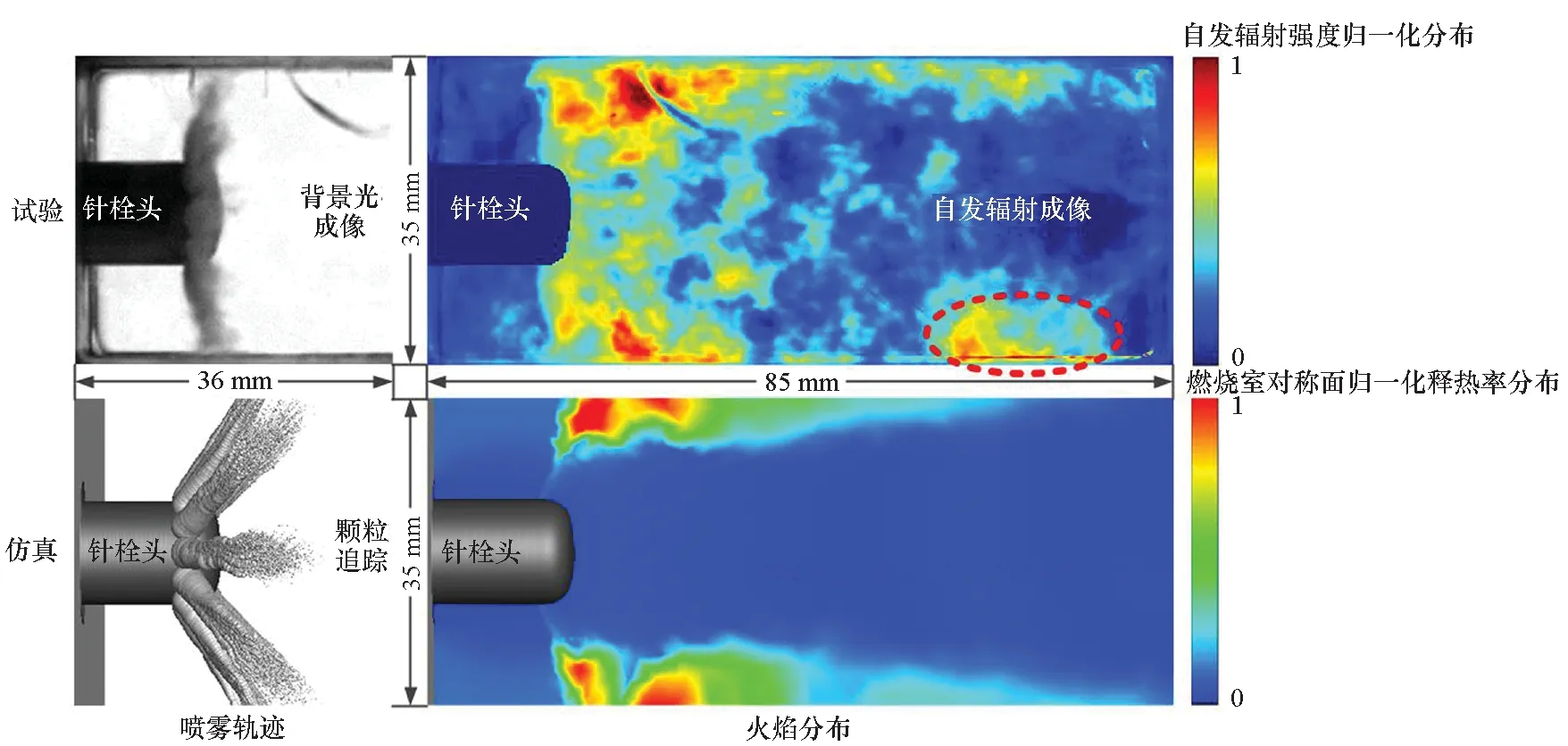
图3 关于喷雾轨迹和火焰形态的试验与仿真结果对比Fig.3 Comparison of experimental and simulation results on spray trajectory and flame distribution
下面针对1.1节给定的无激励设计工况进行分析,图4所示为该工况的燃烧室(P3)和集气腔(P01)压力振荡波形,可以看出:燃烧室压力时均值为1.71 MPa,基本达到设计值(1.8 MPa);燃烧室中段壁面处的无量纲压力振荡幅度P′(1.17%)强于其他位置,未出现燃烧不稳定现象(P′>3%);集气腔压力振荡略滞后于燃烧室压力,且无量纲振荡幅度P′仅为0.15%,这说明燃烧室压力振荡前传至集气腔的过程中出现了极大的耗散。图4中燃烧室(P3)压力振荡波形表现出37 Hz和73 Hz这两个振荡主频,根据文献[15]可知,这两个振荡主频分别由火焰在y方向的摆动过程和液氧的非稳态蒸发过程引起的。

图4 无激励工况下P1与P3处达到稳定的压力振荡波形Fig.4 Stable pressure oscillation wave at P01 and P3 without acoustic excitation
为了区分燃烧室内的火焰模式,这里引入火焰因子FI的概念[19],如式(3)所示。

(3)
从图4选取相隔约半个喷雾火焰摆动周期的两个时刻,相应燃烧流场(见图5)中GCH4来流集中在针栓头下游并维持一定长度的低温区,该低温区伴随燃烧火焰在y方向往复摆动,伴随上下壁面附近回流区尺寸的此消彼长。初始喷注粒径较小(10 μm)的液氧射流在穿透GCH4来流的过程中发生偏转并快速蒸发,未表现出明显的摆动现象。在回流区作用下高温GOX往低温区扩散并与GCH4发生剧烈反应,导致燃烧室内的混合比O/F分布极不均匀。另外,火焰因子的分布也表明燃烧室内的释热反应以扩散火焰为主,且火焰分布区域主要集中于两条混合比等值线(0.5和500)之间。

(a) 内部温度云图及绿色的混合比等值线分布(0.5和500)(a) Interior temperature distribution with mixing ratio iso-lines (0.5 and 500) colored by green
2.2 扰动频率对压力振荡的影响
在t=370.35 ms时刻开启声学激励,不同扰动频率下燃烧室各监测点的无量纲压力振荡幅值如图6所示,当扰动频率与燃烧室1T振荡模态固有频率接近时压力振荡最为剧烈。位于燃烧室头部的监测点(P1和P2)的压力时间历程见图7,f=4 538 Hz时开启速度扰动至稳定振荡阶段(振荡幅度并未完全保持不变)所需的时间间隔最长(约50 ms),相应的压力时均值涨幅最大;在t=475.35 ms时刻关闭速度扰动后燃烧室压力振荡逐渐消失且压力时均值开始下降,约50 ms后压力振荡波形恢复至无激励状态,这说明通过添加速度扰动可产生燃烧室声学振荡响应。随着速度扰动的开启和关闭,集气腔压力出现了相似的变化过程(以f=4 538 Hz为例,见图8),但产生的振荡幅度和时均值的变化幅度均远小于燃烧室压力,这说明燃烧室压力振荡前传至集气腔的过程中出现了极大的耗散,且燃烧室压力振荡并非GCH4喷注引起。

图6 不同扰动频率下各监测点的无量纲压力振荡幅度Fig.6 Dimensionless pressure oscillation amplitude of each monitoring point for different disturbance frequency

(a) f=3 000 Hz
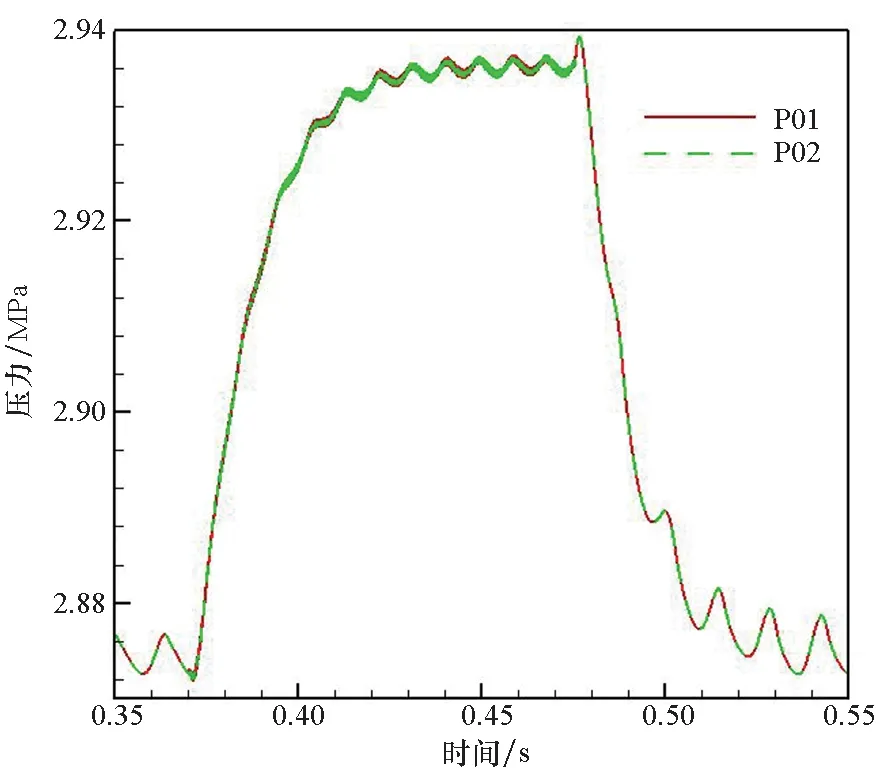
图8 f=4 538 Hz激励条件下集气腔内的压力时间历程Fig.8 Time histories of pressure oscillation in the gas manifold under acoustic excitation with f=4 538 Hz
结合图7中局部放大图和图9所示不同扰动频率下稳定振荡阶段监测点P1处的压力频谱可知,扰动频率变化并未改变燃烧室压力的1T振荡模态,振荡频率均以扰动频率为主,其中f=4 538 Hz时振荡主频对应幅值最大并产生高阶谐振。
2.3 激励条件下的声学响应特性分析
下面结合燃烧流场和声能平衡方程来解释不同扰动频率下喷雾燃烧对声学激励动态响应的差异。从图7中不同扰动频率下的压力振荡波形放大图中选取相隔半个压力振荡周期的两个压力极值点对应的时刻,得到如图10所示的燃烧流场,其中左列包括纵向截面上的温度云图和速度场矢量(以蓝色箭头表示),右列包括液滴分布和z=0平面上的压力场云图,可以看出:激励条件下燃烧室上下壁面附近的相对压力变化符合1T振荡模态,同时速度扰动促进了液氧蒸发和燃烧室前半段GOX/GCH4之间的混合反应,低温区长度缩短。相比于3 000 Hz和6 000 Hz,f=4 538 Hz时喷雾燃烧过程对横向声学激励的响应最为强烈,燃烧室内的回流区结构变化最大,燃烧反应在前半段基本完成,因此温度进一步趋于均匀。Hardi等[9]通过旋转齿轮控制辅喷管出口的开启与关闭,从而对LOX/GH2同轴喷注缩尺火箭发动机施加燃烧室横向声学激励,发现当激励频率等于燃烧室1T振荡模态固有频率时,反应速率(反比于火焰长度)和火焰区域的氢氧基(OH*)自发辐射强度显著强于非共振频率,与本文仿真结果一致。

图9 不同扰动频率下P1处的压力频谱图Fig.9 Spectrogram plots of the pressure trace at P1 for different disturbance frequency
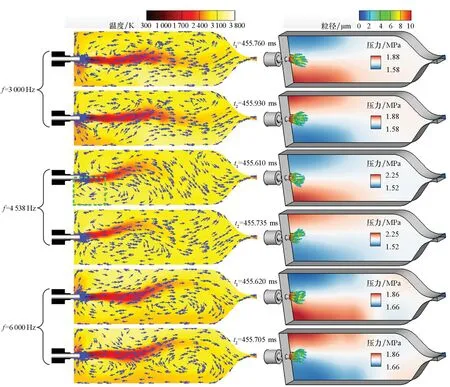
图10 不同扰动频率下相隔半个1T模态压力振荡周期的燃烧流场Fig.10 Snapshots of combustion ow eld with an interval of about half a period of 1T-mode pressure oscillation for different disturbance frequency
另外,在速度扰动作用下燃烧火焰与压缩波(通过速度矢量表示)在y方向发生同步摆动,其中以f=4 538 Hz更为明显,根据Rayleigh准则,燃烧释热将为高压区(波腹)提供能量并维持声学振荡模态。相比之下,针栓喷嘴下游的低温区与液氧液滴分布则在y方向上仅出现同步的小幅摆动现象,原因在于液氧和GCH4来流分别在密度和轴向喷注速度上远大于高温燃气(惯性不同),声学激励对两者的影响较小。
为了进一步定量分析压力和燃烧释热之间的关系,在稳定振荡阶段针对图10中绿色虚线框(0≤x≤0.07 m,-0.07 m≤y≤0)内的流场区域进行积分求解面积平均压力和释热率,压力和释热率之间的关系如图11所示,扰动频率f取3 000 Hz、4 538 Hz和6 000 Hz时指定区域内的平均压力和燃烧释热的同频振荡相位差分别为65.45°、-8.18°和-63.53°,相位差约等于(fc-f)·π/fc,因此在合适的扰动幅值下,相位差由扰动频率与1T模态振荡固有频率之间的相对大小决定。

(a) f=3 000 Hz


(4)
式中,p为压力,Q为燃烧释热,u为速度矢量,ρ为密度,“-”和“′”分别表示平均值和脉动值。
三种扰动频率下压力和燃烧释热的同频振荡相位差在±90°之间,这说明声学激励项S1作用下燃烧释热产生项S2随时间的积分为正,声学源项S大于声能耗散项D,进而维持了燃烧室内的压力振荡幅度;在p′u′项的作用下激励区往无激励区传递声能,因此燃烧室压力振荡幅度沿x方向显著减小。当f=4 538 Hz时压力和燃烧释热基本表现出同相同步的周期性振荡,因此燃烧释热产生项S2及可维持的燃烧室压力振荡幅度均更大,同时该工况下燃烧反应最为充分,外加额外引入的动量源项,使得燃烧室压力时均值超过了设计压力(1.8 MPa);而当关闭速度扰动后,由于燃烧释热产生项S2和流体流动产生项S3无法维持,在声能耗散项D作用下燃烧室压力迅速恢复至无激励条件下的稳定燃烧状态,这说明该针栓式发动机对燃烧室声学振荡具有较强的耗散作用,需采取额外的措施(如本节引入的动量源项)才能维持喷雾燃烧与声学振荡之间的强耦合关系。
最后,以f=4 538 Hz为例分析声学激励对低频振荡的影响。如图7(b)所示稳定振荡阶段的压力振荡幅度的变化对应一个58 Hz的低频振荡(振幅过小,图9中没有体现),图12给出了相隔约半个低频振荡周期的两个时刻的燃烧流场,可以看出,低温区在y方向的摆动幅度较大,而两条混合比等值线(0.5和500)的分布区域相比于无激励工况(见图5)显著减小,这进一步说明燃烧反应基本在燃烧室前段完成,并导致激励条件下低频振荡对应的频率(58 Hz)高于无激励工况(37 Hz),同时混合比等值线在速度扰动作用下出现小尺度波动。火焰因子的分布则显示燃烧室内的释热反应表现出扩散燃烧和预混燃烧并重的特征。另外,火焰除了集中于针栓头附近外,还在速度扰动的作用下广泛分布于燃烧室的一侧壁面附近。

图12 f=4 538 Hz激励条件下相隔约半个低频振荡周期的燃烧室内部温度场(包含绿色混合比等值线(0.5和500))及对称面上的燃烧因子分布Fig.12 Instantaneous interior temperature elds, superimposed on the contour are the mixing ratio iso-lines (0.5 and 500), and FI distributions in the combustor symmetry plane with an interval of about half a low-frequency oscillation period under acoustic excitation with f=4 538 Hz
3 结论
本文采用Euler-Lagrange方法对LOX/GCH4针栓式发动机在不同扰动频率的横向声学激励作用下的声学振荡开展数值模拟,并通过开窗热试证明该计算方法和网格能较为准确地捕捉喷雾轨迹和火焰形态。主要结论如下:采用的声学激励措施能产生同频率的燃烧室1T振荡模态声学响应,喷雾燃烧对声学激励的响应强弱受扰动频率的影响较大,其与燃烧室1T振荡模态固有频率(4 538 Hz)的相对大小决定了压力和燃烧释热相位差;相比无激励工况,速度扰动使得液氧蒸发和GOX/GCH4之间的混合反应均有所增强,低温区长度缩短,存在预混火焰转变为扩散火焰的趋势,进而增大了低频振荡对应的频率;速度扰动关闭后声学源项无法维持导致燃烧室压力迅速恢复至无激励条件下的稳定燃烧状态,这说明该针栓式发动机对燃烧室声学振荡具有较强的耗散作用;由于声能自动从激励区往无激励区传递,稳定振荡阶段燃烧室内的压力振荡幅度沿x方向呈现显著减小的趋势。当扰动频率等于4 538 Hz时达到稳定振荡阶段所需时间间隔最长(约50 ms),此时压力和燃烧释热相位差仅-8.18°,两者接近同相振荡,可维持的无量纲压力振荡幅度高达0.36,且在声学激励这一动量源项作用下压力时均值增长至无激励工况的设计压力(1.8 MPa)以上;同时回流区结构显著改变,喷雾和火焰伴随压力横向振荡出现明显的同步摆动现象。
