自编码器融合极限学习机的广义负荷建模

何怡林，李长安，吴忠强

(1.燕山大学工业计算机控制工程河北省重点实验室，河北 秦皇岛 066004;2.燕山大学河北省重型机械流体动力传输与控制重点实验室，河北 秦皇岛 066004)

0 引言

随着分布式电源与大电网的联合运营，电网结构发生了变化。由于分布式电源存在随机性、变动性等特点，使电力系统互动性增强，电压稳定及频率稳定问题更为突出[1-2]。由于广义电力负荷种类和比例的扩大，节点存在复杂性、波动性、可控性和敏感性等问题[3]，建立精确度高且具时效性的负荷模型，成为电力系统仿真研究及分析的一大难题。

常见的广义负荷建模方法主要分为机理建模方法和非机理建模方法。机理建模方法主要依靠物理和电学的基本定律，如传统的经典模型、增广模型等[4]。现有的许多研究也提出了采用改进的结构模型来等效描述广义负荷特性[5-6]。但机理模型结构易受电源种类及所在比例等因素影响，局限性较大。非机理建模方法将负荷群看作一个“黑箱”，根据负荷母线电压、频率、有功功率和无功功率，建立数学解析函数。文献[7]针对广义负荷在时间变化下难以进行动态建模的问题，提出一种结合聚类分析的非机理建模方法。神经网络具有较强的容错性和鲁棒性，能有效地拟合复杂的非线性函数，所建模型不受负荷成分和特性的限制，为广义负荷建模提供了一条新途径。文献[8]提出将分段函数拟合的思想应用于广义负荷人工神经网络类模型的训练，可以较好地提高人工神经网络模型在广义负荷建模中的泛化能力和稳定性。文献[9]建立了一种基于测量的递归神经网络(recursive neural networks,RNN)广义负荷等效模型。

针对广义负荷模型的多变性、不同分布式能源占比情况下特性难以描述等问题，提出一种基于自编码器融合极限学习机(auto encoder- extreme learning machine，AE-ELM)的建模方法。首先，利用自编码器能降低输入数据维度的优势，提取特征值，通过其最小化重构误差的特点，求得自编码器的编码结构。然后，将此结构用于极限学习机的输入端，即得到已优化隐层节点数的极限学习机结构，完成网络融合。最后，利用极限学习机的监督学习特性，调整隐层至输出层的权值，保证网络收敛至最优值。通过与常用的神经网络进行对比试验，验证了该方法的精确性和有效性。

1 负荷模型

1.1 多项式负荷模型

照明、电热等用电设备采用二次多项式静态负荷模型表示。

(1)

式中：U、P、Q分别为负荷的实际电压、有功功率、无功功率；UN、PN、QN分别为负荷的额定电压、有功功率、无功功率；aP、bP、cP和aQ、bQ、cQ分别为负荷有功和无功多项式静态模型二次项、一次项、常数项的系数，其值均大于0小于1，且满足aP+bP+cP=1、aQ+bQ+cQ=1。

1.2 感应电动机模型

感应电动机模型采用考虑转子电磁暂态的3阶模型[10]。其运动方程如式(2)所示。

(2)

电磁力矩如式(3)所示：

Te=E′dId+E′qIq

(3)

机械负载特性取为转速的2次函数，如式(4)所示：

(4)

1.3 双馈风机模型

双馈风机主要由风力机、齿轮箱、双馈感应发电机(double fed induction generator，DFIG)等组成。

风力机模型[11]如下：

(5)

式中：Pw为风轮转化的风能；ρ为空气密度；Cp()为风能转换效率系数；λ为叶尖速比；β为叶片桨矩角；AR为风轮扫过的面积；vw为风速；Tw为风力机的机械转矩；ωw为风力机的角速度。

DFIG转子运动方程如式(6)所示。

(6)

式中：Te为风力机的电磁转矩；HJ为风力机的转动惯量。

1.4 蓄电池模型

对蓄电池进行建模，其开路电压Uoc和等效串联电阻R0皆是电池荷电状态(state of charge,SOC)的非线性函数[12]，如式(7)所示。

(7)

式中：ib为电池实时充放电电流；CSOC(0)为初始荷电状态；F为电池容量；t为充放电时间。

2 AE-ELM建模

2.1 自编码器

自编码器(auto-encoder，AE)采用无监督的训练方式，能完整、有效地复现输入数据，最小化误差重构，实现数据的特征提取，并减少冗余数据。自编码器可以看作是一种三层的前馈神经网络。输入层和输出层的维度一致，隐层学习并提取输入层特征，是编码(encode)过程；用学习到的新特征重构出原始输入数据，则是解码(decode)过程。三层自编码器结构如图1所示。

图1 三层自编码器结构图

编码过程为：

h=S(w1x+b1)

(8)

式中：x为输入数据特征向量，x=[x1x2...xt]T;w1为编码器的权值矩阵;S()为激活函数。

解码过程为：

(9)

激活函数采用Sigmoid函数，如式(10)所示。

(10)

式中：z为未激活前的变量。

2.2 极限学习机

极限学习机(extreme learning machine，ELM)是一种有监督的学习方法，不需要迭代调参，即可获得唯一的最优解。它的自适应、自主学习能力强，与传统神经网络相比，具有学习效率高、泛化能力强等优势。给定含N个样本的任意训练集(xj,yj)。其中，xj=[xj1xj2…xjn]T∈Rn，yj=[yj1yj2…yjm]T∈Rm。设n为极限学习机的输入层节点数，l为隐层节点数，m为输出层节点数，α为输入层和隐层的连接权值，d为隐层的阈值，β为隐层与输出层的连接权值。

α、β及d的表达式如式(11)～式(13)所示。

(11)

(12)

(13)

激活函数为式(10)，则网络输出为：

(14)

式(14)可简写为：

G=Hβ

(15)

其中：

(16)

式中：H为隐层输出矩阵，H的第i列对应输入第i个隐层输出向量。

α和d在训练前可以随机设定，且在训练过程中保持不变。当激活函数无限可微时，隐层与输出层的连接权值β不需要迭代调整，通过以下方程组的最小二乘解来求解。

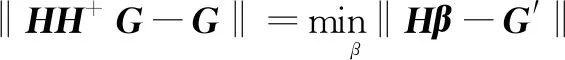
(17)

其解为：

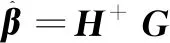
(18)

式中：H+为隐含层输出矩阵H的Moore-Penrose广义逆。

2.3 AE-ELM的广义负荷建模

自编码器融合极限学习机，是将AE的降维思想应用到ELM中，既可以挖掘出输入数据的内在有效特征，又进一步提高了算法效率。首先，利用AE能降低输入数据维度的优势，提取特征值，通过其可最小化重构误差的特点，求得AE编码结构。然后，将此结构作为ELM的输入端结构，可以有效解决ELM隐层节点数难以确定的问题。最后，通过ELM的有监督学习方法，调整隐层至输出层的权值，保证网络收敛至最优值。AE-ELM模型结构如图2所示。

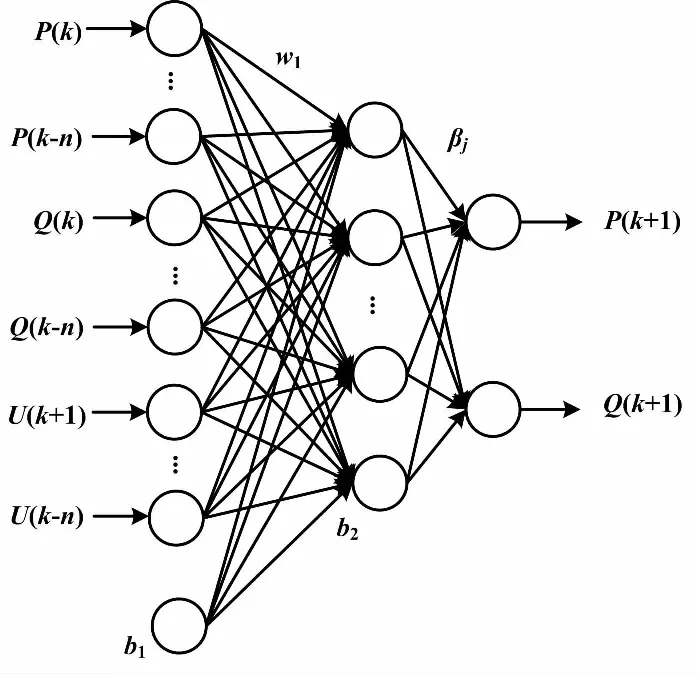
图2 AE-ELM模型结构图

设f(P,Q)为广义负荷系统模型的一般描述，可建立关系式如下：

[P(k+1),Q(k+1)]=f(P,Q)[P(k),P(k-1)，...,P(k-n),Q(k),Q(k-1),...,Q(k-n),U(k+1),U(k+2)，...,U(k-n)]

(19)

式中：P(k+1)和Q(k+1)分别为第(k+1)时刻的有功功率标幺值和无功功率标幺值；P(k),P(k-1)，...,P(k-n)为第k时刻及之前n个时刻的有功功率标幺值;Q(k),Q(k-1)，...,Q(k-n)为第k时刻至之前n个时刻的无功功率标幺值；U(k+1),U(k+2),...,U(k-n)为第(k+1)个时刻至之前(n+1)个时刻的电压标幺值。

基于AE-ELM的建模过程，首先需要循环取多个样本集，进行数据预处理，并训练AE结构；然后，根据误差变化情况，获取临界处的隐层节点数，进而得到已优化的ELM隐层结构；最后计算ELM隐层至输出层的权值，得到最终模型结构。AE-ELM建模训练流程如图3所示。

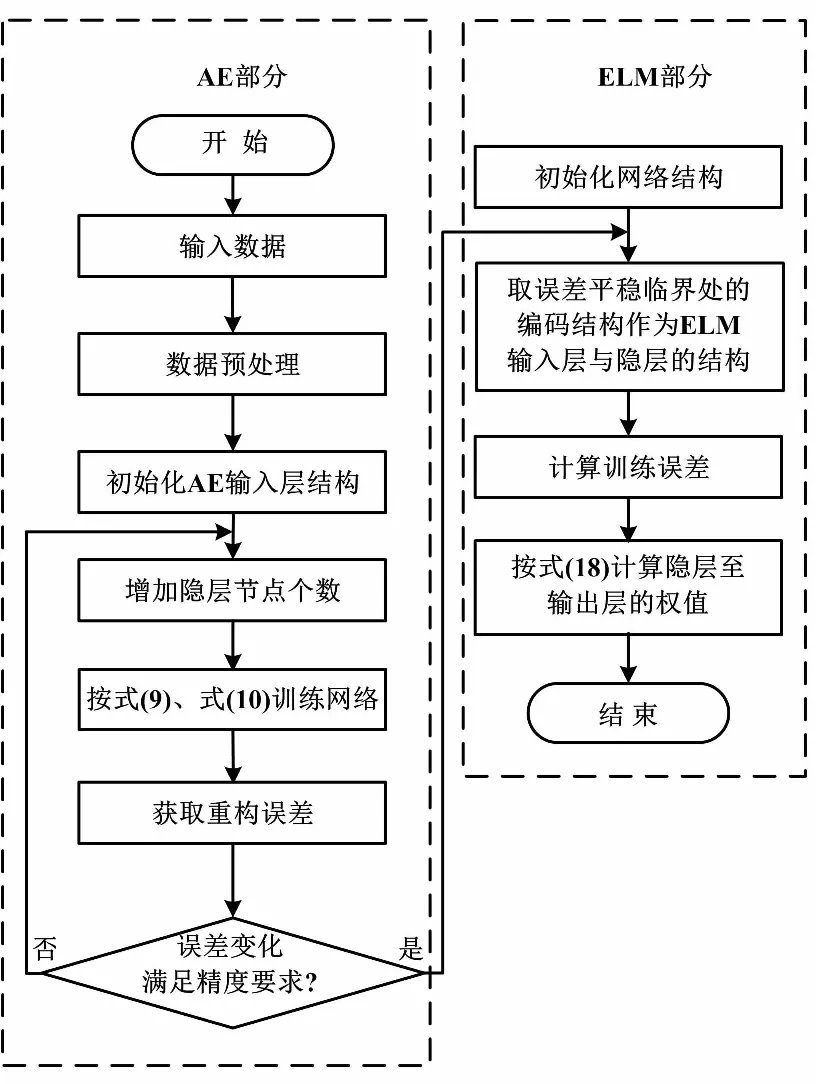
图3 AE-ELM建模训练流程图

3 仿真算例

利用MATLAB建立仿真系统，其电气接线如图4所示。图4中：G为系统网侧发电机，Z为恒阻抗负荷模型，其统一参数为aP=0.3、bP=0.5、cP=0.2、aQ=0.6、bQ=0.25、cQ=0.15。M为感应发电机，其主要参数为：XS=0.091 H，Xm=2.23 H，XR=0.071 H，RS=0.064 Ω，RR=0.059 Ω，H=8 368 kg·m2，A=0.5，B=D=0.2，C=0.1，α=0.2。DFIG为风力发电机组，由6台额定功率为1.5 MVA的风机组成。设定风速vw=11 m/s近似不变，单台风机的主要参数为ρ=1.225 kg/m3、Cpmax=0.48、λ=5.81、HJ=15 856 kg·m2。蓄电池的主要参数为：F=100 A·h，Uoc=300 V，R0=26 mΩ。

图4 仿真系统电气接线图

3.1 不同电压扰动下的建模测试

电压跌落50%时的功率曲线如图5所示。为说明AE-ELM方法的有效性，将其与常用神经网络进行比较。其中，反向传播(back propagation,BP)、径向基函数(radial basis function,RBF)、ELM的网络结构设置与AE-ELM结构相同，以保证公平性。

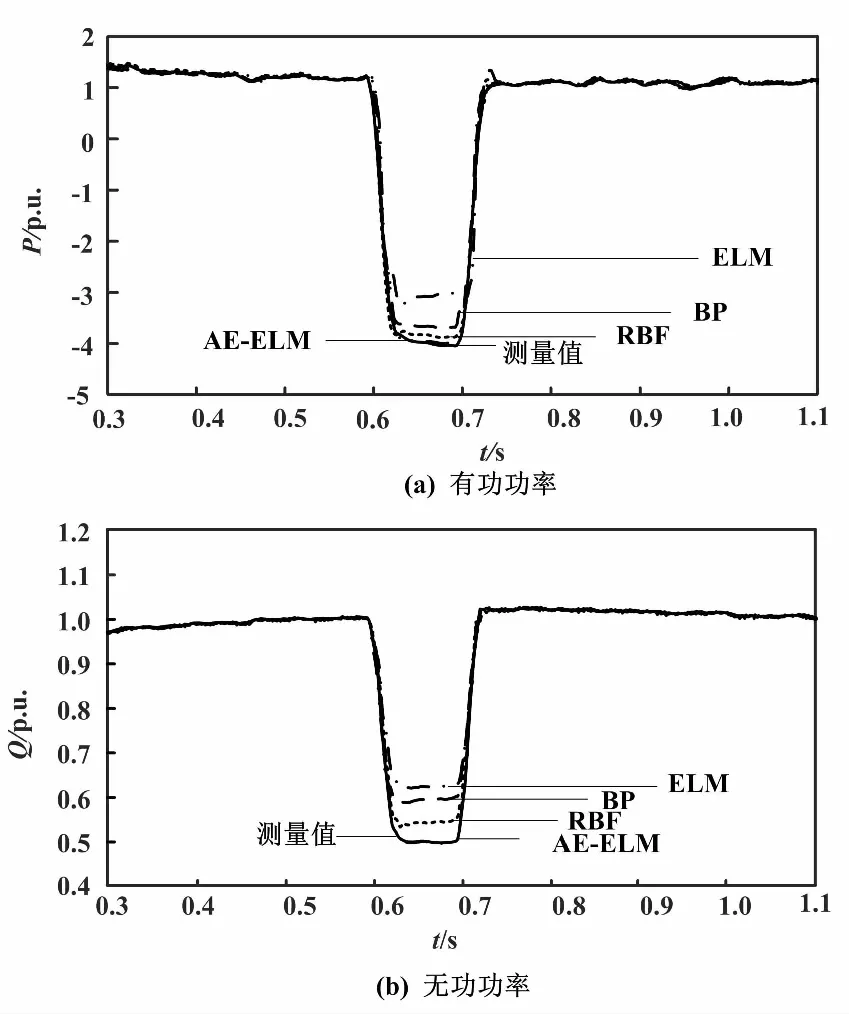
图5 电压跌落50%时的功率曲线图

设仿真时间为2 s，采样周期为0.000 1 s。在负荷母线B2节点处设置不同程度的三相短路故障，使母线电压标幺值下降区间为20%～85%，在0.6 s时发生故障，0.7 s时故障解除。在扰动下，测得负荷母线处的电压、有功功率及无功功率标幺值。电压标幺值每下降5%测量一次数据，将测量数据的三分之二作为训练集，三分之一作为测试集，建立广义负荷模型。选取n=5，可得AE-ELM网络输入维数为16、通过训练确定AE的隐层节点数为11，既满足了所需的精度要求，又确定了ELM的隐层节点数为11。

为了更精确地比较建模效果，定义模型的有功功率与无功功率的绝对平均误差如式(20)、式(21)所示。

(20)

(21)

式中：P′i和Q′i分别为网络输出的第i个有功功率和无功功率数据;Pi和Qi分别为系统第i个有功功率和无功功率的测量数据；O为记录的数据长度。

表1给出了4种建模方法在电压跌落50%时的绝对平均误差情况。

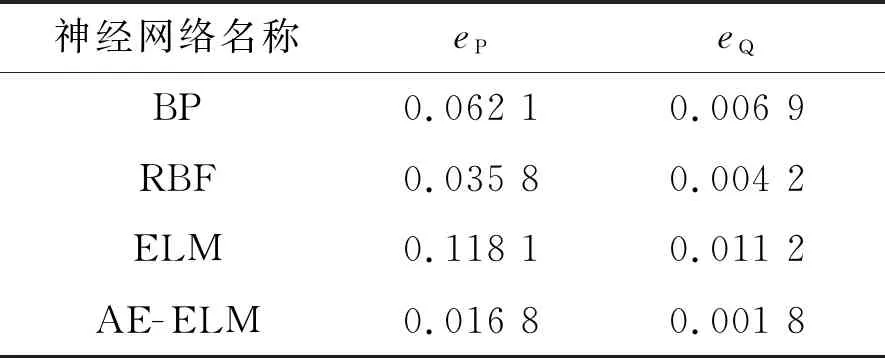
表1 电压跌落50%时的绝对平均误差

从表1可以看出，在同等网络结构下，AE-ELM模型拟合效果最好，其次是RBF神经网络模型，最差的是ELM网络。AE-ELM网络较BP、RBF与ELM网络的有功功率绝对平均误差分别下降了72.9%、53.1%和85.8%，无功功率绝对平均误差分别下降了73.9%、57.1%和83.9%。这说明AE-ELM可以比传统的BP、RBF及ELM网络更为精确地描述广义负荷系统的节点特性。

3.2 不同风机容量下的建模测试

设负荷母线节点B1处在0.8 s时发生三相短路故障，0.9 s时恢复正常，电压跌落50%。在此故障条件下，设定风机容量占比由20%增加至80%，每增加5%测量一次，将测量数据的三分之二作为训练集、三分之一作为测试集。风机容量占比为65%时的功率曲线如图6所示。

图6 风机容量占比为65%时的功率曲线图

风机容量占比为65%时的绝对平均误差如表2所示。从表2可以看出， AE-ELM网络绝对平均误差最小，且较RBF、BP与ELM网络的有功功率误差减少了至少37.0%以上、无功功率误差减少了至少50%。

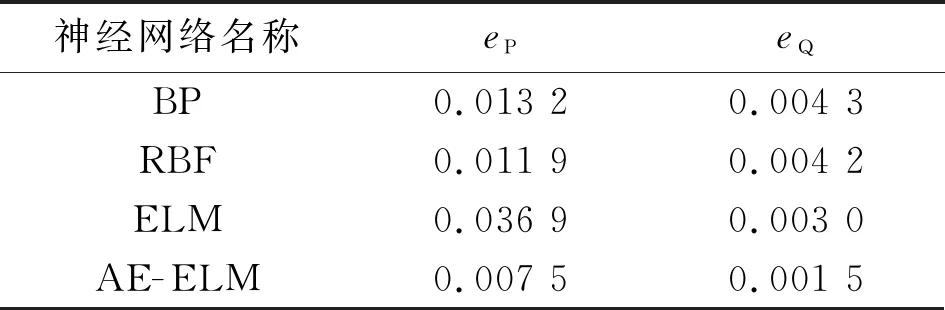
表2 风机容量占比为65%时的绝对平均误差

不同电压扰动下的建模测试和不同风机容量下的建模测试均表明AE-ELM网络优于RBF、BP与ELM网络。这主要是因为BP网络采用梯度算法，调整的参数较多，存在易陷入局部最小值和隐层节点数难以确定等问题；RBF网络具有较强的局部逼近能力，但存在基函数的中心点和隐层节点数难以确定等问题，影响逼近效果；ELM网络训练强依赖于隐层结构的调整，对输入数据维度要求较高；AE-ELM融合了AE网络的降维特性和ELM网络较强的非线性拟合能力，解决了ELM网络隐层结构难以确定的问题。

4 结论

为解决负荷成分和特性的限制，本文提出了一种基于自编码器融合极限学习机(AE-ELM)的广义负荷建模方法。该方法利用自编码器的降维特性，并结合极限学习机不需要迭代调参的优势，可加快训练速度，并且易于控制、通用性好，具有较强的非线性拟合能力等特点，可实现高精度建模。对含有双馈感应发电系统与蓄电池并网的广义负荷系统进行建模测试，与常用的BP、RBF、ELM网络相比，AE-ELM网络可以更加准确地描述广义负荷系统的特性，由此验证了AE-ELM建模的有效性。随着广义负荷成分复杂度的增加，该方法的优势将更为显著，可以有效地应用于各类广义负荷建模。