基于特征放大的小波反应堆CRDM动作检测

徐鸣睿,朱振杰,霍孟友,李建伟

(1.山东大学机械工程学院,山东 济南 250100; 2.山东核电有限公司,山东 烟台 264010)

0 引言

控制棒驱动机构(control rod drive mechanism,CRDM)是用于驱动控制棒的装置，是反应堆内的核心部件。反应堆通过控制棒驱动机构来实现对控制棒的提升与插入，从而控制反应堆功率以及反应堆安全启停。

目前，国内核电站广泛采用了磁力驱动型CRDM[1]。该CRDM通过三组线圈的交替配合来实现控制棒的步进运动。如果控制棒行进过程中钩爪动作出现异常，可能导致控制棒无法到达预期的位置，严重时甚至会导致控制棒意外下落[2-3]。线圈电流上的动作点可用于识别该故障，但是国内核电站中普遍缺少对该动作点的监测手段，因此设计一种对控制棒驱动机构线圈电流上动作点进行可靠检测的方法极其重要。针对控制棒驱动机构线圈电流的动作点检测问题：文献[4]提出对动作点部分进行微分，判断是否有小于零的值，但要求电流曲线及动作点处于较为理想的条件下；文献[5]提出使用小波变换对动作点进行识别，经小波分解后的信号在第五层可较为明显地看出动作点与非动作点的差异，但是其差异度不是很高，易受到噪声的干扰，辨识存在风险。

为实现对控制棒驱动机构线圈电流动作点的可靠检测，本文设计了基于特征放大的小波检测算法。首先，对控制棒驱动机构线圈电流上升段建立模型，通过建立的模型突出动作点的特征，实现对动作点的特征放大；然后，对特征放大后的动作点进行小波分解检测。检测结果表明，这种方法相较于相同条件下的小波变换具有更好的辨识度。

1 控制棒驱动机构结构及动作原理

控制棒驱动机构包含有驱动轴、钩爪、衔铁、线圈等部件。控制棒驱动机构结构如图1所示。一组控制棒驱动机构中包含有提升线圈、锁紧线圈、固定线圈各一个，磁通环与线圈构成电磁铁，电磁铁的通电与否可用于控制钩爪的运动，三个线圈按一定的时序密切配合，实现驱动棒的提升与插入[6]。以提棒为例：当需要将驱动轴提升一步时，先是锁紧线圈通电，使锁紧钩爪抱住驱动轴；然后固定线圈断电，使固定钩爪脱离驱动轴；最后提升线圈通电，将锁紧钩爪连同驱动轴一起向上提升一步。

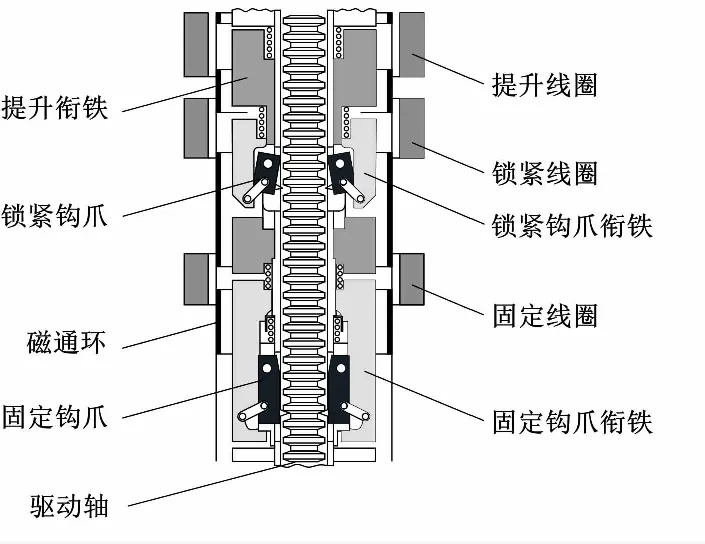
图1 控制棒驱动机构结构示意图

因为驱动轴的提升与插入需要各个部件之间的密切配合，所以稍有差错即可能导致相应的钩爪动作失败。其在控制棒驱动机构线圈电流图上表现为动作点的缺失。正常情况下，线圈电流增大，钩爪会产生相应的动作。而钩爪产生动作后会引起磁通量的减小，造成线圈电感增大、电流减小，并在线圈电流图上产生一个类似于回沟的动作点[7]。一旦出现异常，该动作点将会消失。正常状态下，控制棒驱动机构提升一步线圈电流如图2所示。

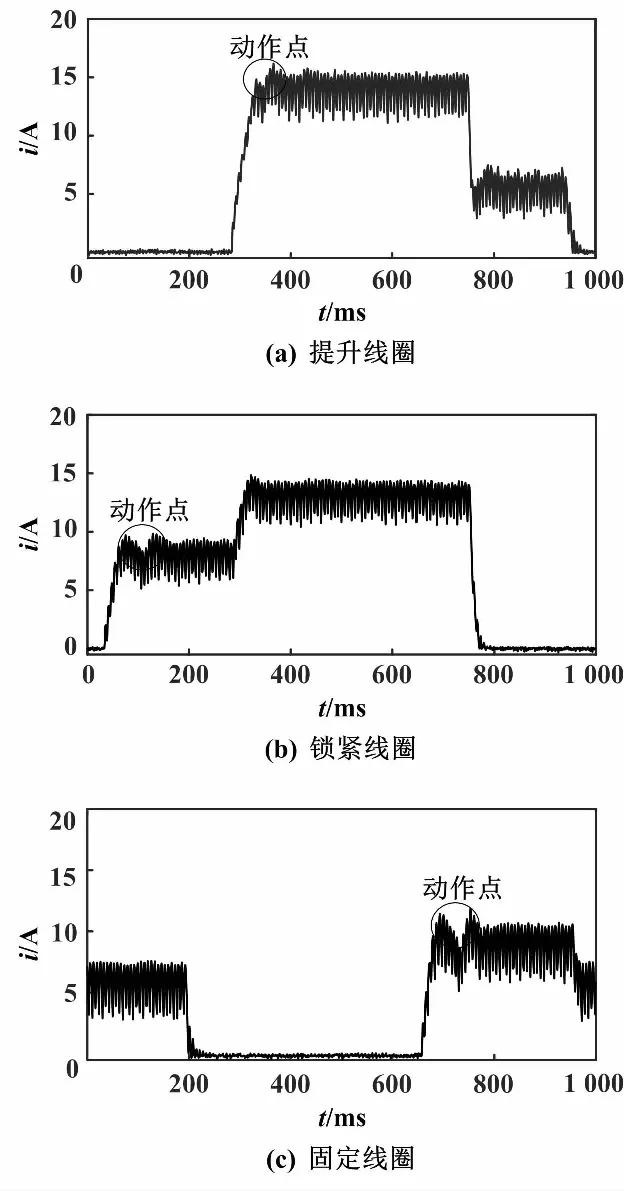
图2 提升一步线圈电流(正常状态)

以提升一步时的提升线圈为例，异常状态提升一步线圈电流如图3所示。

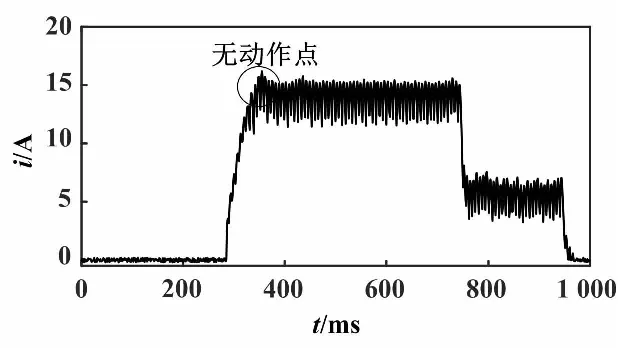
图3 提升一步线圈电流(异常状态)

2 检测原理

对控制棒驱动机构线圈动作点的检测方法是小波奇异点检测，通过检测后的结果来判断控制棒驱动机构的动作是否成功。

通常将信号奇异点分为两类。第一类奇异点是信号幅值在某时刻发生变化，在该处产生一个奇异点，信号不再连续。第二类奇异点是信号的一阶微分产生突变，但原始信号仍然是连续的[8]。

对信号的奇异点进行检测就相当于在不同尺度上对信号进行“磨光”，本质是对原始信号进行滤波，然后对“磨光”后信号的一阶或者二阶导数的零点或者极值点进行检测。

信号奇异点检测的原理如下。

设f(t)是k(t)和g(t)的卷积。

f(t)=k(t)⊗g(t)

(1)

根据傅里叶变换的性质可得：

F[f′(t)]=F[k′(t)]G(ω)=F[g′(t)]K(ω)

(2)

式中：G(ω)和K(ω)分别为g(t)和k(t)的傅里叶变换。

进一步微分可得：

f′(t)=k′(t)⊗g(t)=g′(t)⊗k(t)

(3)

根据式(3)可知，如果将k(t)作为原始信号，将g(t)作为滤波器，则原始信号与滤波器导数的卷积与滤波器与原始信号的卷积相同。因此，原始信号经过小波变换后的突变点或者极值点与原始信号的奇异点相对应，可以利用小波变换来检测信号的奇异点。

使用θ(t)表示“磨光”函数，θ(t)起到低通滤波的作用，通常使用高斯函数或者B-样条函数，且一般满足如下的条件：

(4)

(5)

设θ(t)为二次可导函数，有如下定义：

(6)

(7)

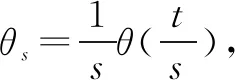
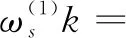
(8)

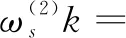
(9)

根据式(8)和式(9)可知，尺度因子s的大小对小波函数平滑后的结果有显著的影响。当尺度因子s较小时，小波函数对原始信号k(t)的奇异点的平滑效果较小；当尺度因子s较大时，小波函数对原始信号k(t)的平滑效果比较明显，k(t)较小的奇异点将会被平滑掉，只有较大的奇异点将会被保留。由此可知，当小波函数为某一平滑函数的一阶导数时，原始信号经小波变换后呈现的局部极值与原始信号的奇异点对应；而当小波函数为某一平滑函数的二阶导数时，原始信号经小波变换后呈现的过零点与原始信号的奇异点对应[9-10]。

3 检测模型

如图2所示，所有动作点均出现在上升段末端，且提升线圈中的动作点幅度最小，难以识别。如果对局部信号特征进行放大，就可以很容易地对动作点进行辨识。现以提升线圈为例：对提升线圈电流信号进行滤波以及后续建模后，使用基于特征放大的小波变换识别控制棒驱动机构的动作。

3.1 线圈电流滤波

由于采集到的线圈电流信号中包含较多的噪声信号，为防止噪声信号对动作点分析的影响，在进行小波分析前，需要对线圈电流信号进行数字滤波。

对信号的频谱进行分析，发现电流信号的有效部分主要集中在信号的低频段。提升线圈电流信号频谱如图4所示。

图4 提升线圈电流信号频谱图

对电流信号采取低通滤波，选用切比雪夫I型数字低通滤波器，通带截止频率选择为28 Hz，阻带截止频率选择为33 Hz。经过低通滤波后，大部分噪声被滤除干净，剩下部分噪声未对动作点部分形成明显的影响，动作点能较为清晰地显示。提升线圈电流滤波信号如图5所示。

图5 提升线圈电流滤波信号

为保证算法识别的准确性，仅对信号的上升段进行分析。首先对提升线圈包含动作点部分的上升段进行截取，截取部分为图5中300～380 ms的曲线。由此获得的提升线圈电流上升段如图6所示。

图6 提升线圈电流上升段示意图

3.2 电流上升段模型构建

控制棒驱动机构电路如图7所示。图7中：R为工作线圈的内阻；L为线圈的等效电感；VT1为逆变管，用于控制电流时序；VT2为斩波管，用于控制电流的大小；R0为一个耗能电阻。当VT1和VT2都不导通时，R0可用于释放工作线圈中产生的自感电动势[11]。

图7 控制棒驱动机构电路图

根据图7所示的电路图，由基尔霍夫电压定律可得到相应的电路方程：

(10)

式中：E为线圈的电压；L为磁路的等效电感；I为线圈上的电流；R为线圈的等效电阻；x为线圈位移。

因为磁路的电感值会随着线圈的移动而发生改变，所以磁路的等效电感L是一个以线圈位移x为自变量的函数。

在线圈电流上升的初段，线圈的位置不变。此时，若假设L的值不发生变化，则式(10)可以简化成式(11)。

(11)

式(11)为一个零状态响应方程，可以推得线圈电流的大小为：

(12)

当线圈电流信号中不包含动作点时，表示钩爪的动作没有完成。此时，线圈的位置没有发生变化，即电感值也没有改变。所以可以根据推导出的线圈电流计算式，对线圈电流上升段曲线进行拟合，最终得到线圈电流上升段模型。

(13)

将拟合得到的模型与无动作点信号的上升段进行比较，得到的无动作点上升段模型与实际无动作点上升段对比如图8所示。由图8可以看出，构建的模型能较好地拟合无动作点电流上升段曲线，表明建立的无动作点线圈电流上升段模型是准确的。

图8 无动作点上升段模型与实际无动作点上升段对比图

3.3 模型构建

含动作点的线圈电流信号和无动作点的线圈电流信号之间的差值就是动作点信号，与高斯函数的一阶导数相似。使用高斯函数的一阶导数来拟合动作点，数学表达式如下：

(14)

式中：a为信号的幅值；μ为信号相对于y轴的偏移量；σ为信号的平缓程度。

根据实际信号，可以计算得到a=3.4、μ=53、σ=10。

将得到的动作点模型与前面建立的无动作点的上升段模型进行叠加后，构建含动作点电流曲线上升段模型。将模型与图6中的含动作点电流上升段进行对比，得到的含动作点上升段模型与实际含动作点上升段对比如图9所示。

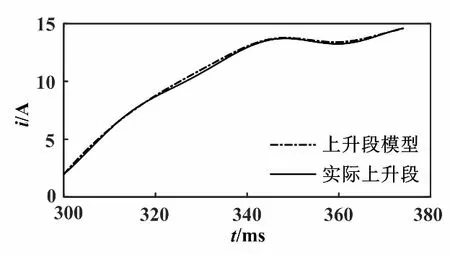
图9 含动作点上升段模型与实际含动作点上升段对比图

由图9可以看出，构建的含动作点电流上升段模型能较好地拟合含动作点电流上升段曲线，表明建立的含动作点线圈电流上升段模型是准确的。同时，含动作点电流上升段曲线的动作点部分可通过建立的模型进行特征放大。

3.4 检测结果对比分析

利用无动作点电流上升段模型，对动作点部分进行特征放大，使用含动作点电流上升段曲线减去已建立好的无动作点电流上升段模型，也就是“放大”后的动作点部分。含动作点上升段与无动作点上升段对比如图10所示。

图10 含动作点上升段与无动作点上升段对比图

为验证算法效果，在MATLAB平台中选用小波基函数sym2对特征放大后的动作点部分使用小波变换，得到的小波分解第五层高频系数结果对比如图11所示。

图11 小波分解第五层高频系数结果对比图

为便于对结果进行分析，将小波变换后曲线中最大幅值与最小幅值之间的差值定义为该曲线的幅值差，将相同条件下含动作点曲线的幅值差与无动作点曲线的幅值差之比定义为动作点的辨识度。辨识度越大，含动作点曲线与无动作曲线间的差异就越大，可设定的辨识度阈值范围也越大。这就能更方便地分辨两种曲线，表明对动作点的检测更可靠。

由图11可知，基于特征放大的小波变换中含动作点曲线的幅值差为1.056 A-0.812 A=1.868 A，无动作点曲线的幅值差为0.098 A-(-0.1 A)=0.198 A，可算得基于特征放大的小波变换中动作点的辨识度为1.868÷0.198=9.43。同理可算得小波变换中动作点的辨识度为3.249÷1.382=2.35。两种方法的小波分解比较结果如表1所示。

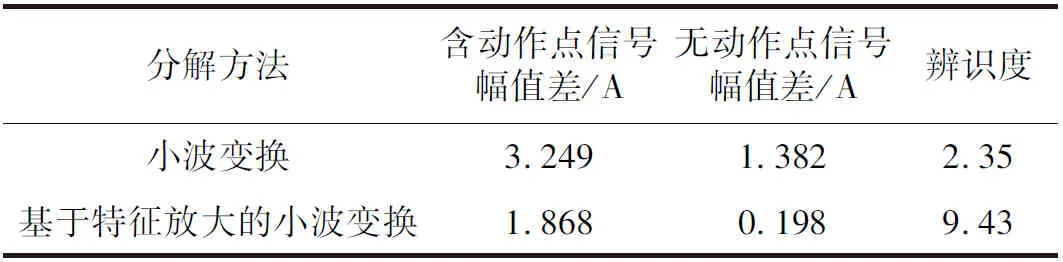
表1 两种方法的小波分解比较结果

由表1可知，使用基于特征放大的小波变换动作点检测方法后，动作点的辨识度由2.35提升至9.43，辨识度阈值范围由1～2.35提升至1～9.43。因此，可在辨识度1～9.43的范围内选取一个合适的辨识度阈值，即可将含动作点信号与无动作点信号较为容易地区分开来。由此可见，与纯小波变换动作点检测方法相比，基于特征放大的小波反应堆CRMD动作检测方法有更高的辨识度及更大的辨识度阈值选取范围，所提供的检测效果更为可靠。

4 结论

本文针对控制棒驱动机构动作点检测可靠性的要求，在小波变换检测控制棒驱动机构动作原理研究的基础上，设计了基于特征放大的小波反应堆CRDM动作检测方法，建立了无动作点电流上升段模型以及电流动作点模型。利用无动作点电流上升段模型对电流动作点的特征进行放大。该模型较好地拟合了无动作点电流上升段曲线和含动作点电流上升段曲线，表明所建模型的准确性。而检测对比分析结果表明，相较于纯小波变换动作点检测方法，基于特征放大的小波反应堆CRDM动作检测方法的辨识度更高、辨识度阈值可选取范围更大，可以提供更为可靠的反应堆控制棒驱动机构动作点检测。