基于马尔可夫过程的快速SIL验证方法研究
2021-10-09崔铭芳杜炘洁
付 进,张 渺,崔铭芳,杜炘洁
(中国石油西南油气田分公司安全环保与技术监督研究院,四川 成都,610041)
0 引言
近年来,社会对工业过程安全日益重视,安全仪表系统的应用也越来越普遍。为保证新建或改造的安全仪表系统能够满足现有的生产工艺需求,将生产风险控制在合理、可接受的范围内,需要对安全仪表系统开展安全完整性等级(safety integrity level,SIL)评价[1]。这也是完整性管理体系中的重要环节[2]。目前,常用的方法主要包括可靠性框图[3]、故障树[4]、马尔可夫(Markov)模型法[5-6]等。其中,Markov模型法对安全仪表系统的各方面因素考虑全面。但该方法运算量大,时间成本相对较高。尤其在安全性能要求高的高冗余系统(例如大型高含硫天然气净化厂的安全仪表系统)中,Markov模型法的缺陷将被进一步放大,因此并未得到广泛应用。
郭海涛等[7]通过对状态转移矩阵预先迭代相乘来降低计算量;Brissaud等[8]通过部分测试和全面测试的试验分析,提出一种简化的计算方法;王海清等[9]提出一种多阶段马尔科夫模型简化算法。这些方法在一定程度上减少了计算量,但其实质都是通过数学近似来简化运算,从而引入了计算误差。因此,本文以Markov过程理论为基础,提出了快速马尔可夫方法(rapid Morkov,R-Markov)。该方法在保证计算精度的前提下显著降低时间成本,能够应用于大规模的安全仪表系统的SIL验证。
1 Markov模型法计算平均要求时失效概率
1.1 SIL定级计算方法
安全仪表系统的SIL定级本质是计算系统中安全仪表功能(safety instrumentation function,SIF)的平均要求时失效概率(probability of failure on demand,PFD)。该概率值pa为回路中传感器、逻辑单元、最终元件的平均要求时失效概率ps、pl、pfe之和[10]。
pa=ps+pl+pfe
(1)
SIL与PFD的关系如表1所示。

表1 SIL与PFD的关系
根据每个安全仪表功能的平均要求时失效概率大小,验证其是否满足所需 SIL要求。如果计算所得的概率小于或等于相应SIL等级的失效概率,说明按现有的配置状态满足SIL的要求;反之,则说明按现有的配置状态不满足所需SIL的要求,要对现有配置中的某一个元件或某几个元件的冗余配置进行改进,例如逐级增加冗余配置。对于改进后的安全仪表功能作再次计算,直到最终概率满足要求为止[11]。
1.2 Markov模型法
Markov模型法基于Markov过程理论,将系统划分为若干独立状态,状态间会以特定概率相互转移。系统将来所处的状态和系统的历史状态无关,只和当前状态有关。Markov模型的这个特性恰好能够解决电子电气系统失效的指数概率密度问题。因此,Markov模型很适合用来进行安全仪表系统失效分析,包括多个影响可靠性的因素,例如结构冗余、共因失效、自诊断、在线或离线测试维修、非理想的维修测试、周期性功能测试、单一或多个维修队伍等。本文涉及的可靠性参数及计算方法如表2所示。表2中,M、S、Cd、CS、β分别代表平均修复时间、装置误动作重启时间、危险覆盖因子、安全覆盖因子以及共因失效因子。

表2 可靠性参数及计算方法
安全仪表系统的过程周期由启动、运行、失效以及修复后再运行等一系列事件序列组成。通过Markov模型可以高效、高精度地模拟系统中的静态关系和复杂的动态变化。但模型的状态数量会随系统的复杂程度递增。如果一个组件有5种失效模式,那么包括正常状态在内共有6种状态,对应的是6维状态转移矩阵。1oo2系统状态转移模型如图1所示。
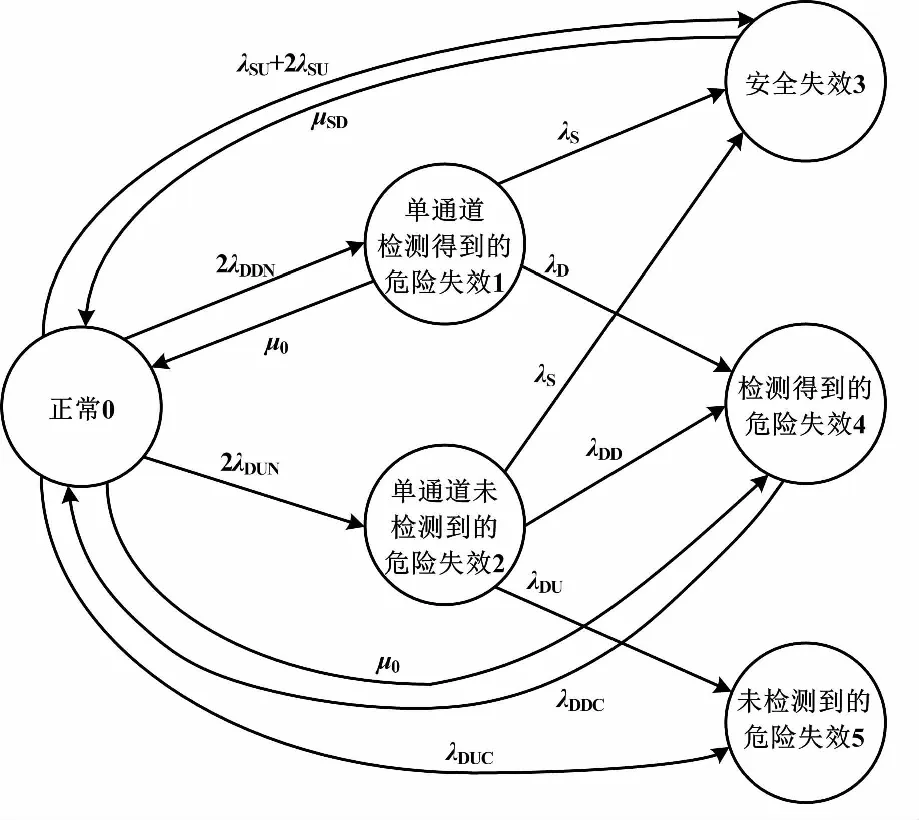
图1 1oo2系统状态转移模型
在状态0,两个通道都可以正常运行。在状态1和状态2,一个通道发生危险失效,但另一个通道仍可执行安全功能,系统仍处于安全状态。另外,状态1的危险失效被检测到后可以进行在线修复,以修复率μ0回到状态0。状态3、状态4、状态5都是系统失效状态:状态3表示系统发生安全失效,状态4表示系统发生检测得到的危险失效,状态5则代表系统发生未检测到的危险失效。当发生共因失效时,系统从状态0直接跳转到状态4或状态5。状态转移矩阵P如式(2)所示。其中,∑表示矩阵元素所在行除该元素外其他元素之和[12]。
(2)
转移矩阵P的元素Pij代表在一个时间段里,系统由状态i转移到状态j的概率。定义初始状态向量S0。该向量在1oo2结构中为6维,代表系统共有6种状态。若系统初始状态正常,则S0=[1 0 0 0 0 0]。经过一个时间间隔,系统处于各状态的概率向量S1=S0P。经过两个时间间隔后,系统处于各状态的概率向量S2=S1P。以此类推,Sn=Sn-1P或Sn=S0Pn。显然,系统越复杂,存在的状态数越多,状态向量S的维数越多,转移矩阵P越复杂,求解P的n次幂时花费的时间也指数倍增加。
假设第6个状态为未检测到的危险失效状态、第5个状态为检测到的危险失效状态、第4个状态为安全失效状态,则定义危险失效向量Vd=[0 0 0 0 1 1]T,安全失效向量Vs=[0 0 0 1 0 0]T。假设测试周期T为一年,约为8 760 h。经过i小时后,系统状态向量Si、要求时失效概率di为:
Si=S0Pi,i=1,2,...,8 760
(3)
di=S0PiVd,i=1,2,...,8 760
(4)
平均要求时失效概率为:
(5)
通过式(5),分别计算出安全仪表功能中传感器、逻辑单元、最终元件的平均要求时失效概率。由式(1)可求得所在SIF平均要求时失效概率,从而得到SIL等级。
2 Markov模型法优化分析
2.1 Markov模型法时间复杂度分析
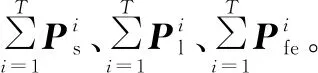
(6)
由式(6)可知,随着T和n取值的增大,计算时间将呈指数上升。而T的取值通常大于8 760。这也是目前Markov模型法在SIL验证中应用较少的原因。对于大型安全仪表系统,出于时间成本考虑,一般会选择其他方法。
2.2 Markov转移矩阵幂运算优化
由式(6)可知,时间开销主要来自矩阵高次幂的累计求和。而由矩阵理论可知,如果方阵可以相似对角化,则存在对角矩阵D和可逆矩阵U,使P=UDU-1成立。Pi可由式(7)计算:
Pi=(UDU-1)i=UDU-1UDU-1×...×UDU-1=UDiU-1
(7)
对角矩阵D的元素对应转移矩阵P的特征值λ,因此Pi的计算就简化为求P的n个特征值λ1、λ2、...、λn的i次幂。式(8)为优化后算法计算平均要求时失效概率时的计算式。
i=1,2,...,8 760
(8)
该算法的时间复杂度为:
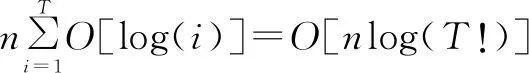
(9)
相比式(6)中的O(T2n3),优化后的时间复杂度显著降低。随着系统冗余程度的提高和测试周期的提高,即n和T越大,算法效率提升越明显。但要使上面的结论成立,需要证明Markov转移矩阵可以相似对角化。
2.3 证明转移矩阵可相似对角化
矩阵可相似对角化的定义为:n阶方阵存在n个线性无关的特征向量。该问题可转化为求证方阵特征值互异。
(10)
考虑式(10)所示1oo1系统的转移矩阵P,求解满足特征方程|λE-P|=0的特征值λ,如式(11)所示。
(11)
式(11)化简可以得到特征方程,如式(12)所示。
(λ-1)[λ3+λ2(λDD+λS+μ0+μSD-3)+λ(λDμ0+λDμSD-2λD-λDμ0+λSμ0-2λS+μ0μSD-2μ0-2μSD+3)+λDμ0μSD-λDμ0-λDμSD+λD-λDDμ0μSD+λDDμ0-λSμ0+λS-μ0μSD+μ0+μSD-1]=0
(12)
由式(12)可知:P中的一个特征值λ1=1,λ2、λ3、λ4为方程剩余项的解,方程中λS、λD、λDD数量级范围为10-8~10-5,危险失效恢复率μ0、安全失效恢复率μSD分别为元件平均修复时间和装置误动作重启时间的倒数,数量级范围为10-2~10-1。将式(12)中失效参数按数量级合,并将特征方程简化为f(λ)=λ3+Aλ2+Bλ+C。令f(λ)=0,A、B、C近似取值范围分别为(-2.927,2.833)、(2.671,2.855)、(-0.838,-0,928)。网格分区生成特征方程曲线族,均与x轴相交于三个不同点,则λ2、λ3、λ4三个特征值互异。特征方程曲线如图2所示。
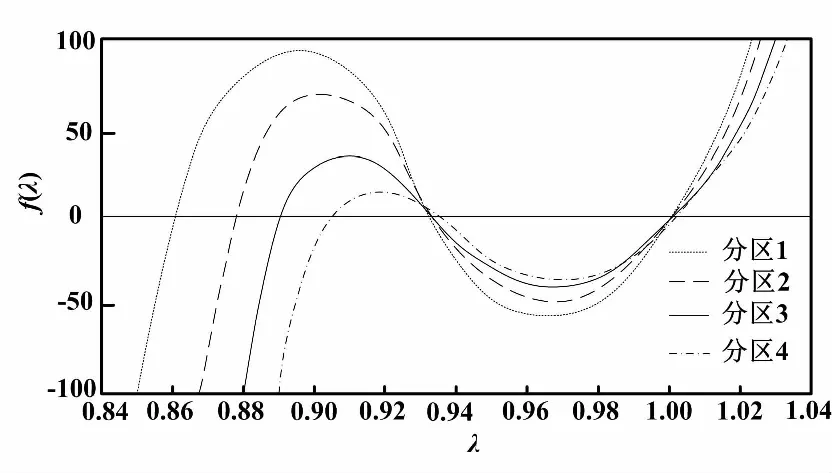
图2 特征方程曲线
将λ=1代入三次特征方程,得:
1+λDD+λS+μ0+μSD-3+λDμ0+λDμSD-2λD-λDμ0+λSμ0-2λS+μ0μSD-2μ0-2μSD+3+
λDμ0μSD-λDμ0-λDμSD+λD-λDDμ0μSD+λDDμ0-λSμ0+λS-μ0μSD+μ0+μSD-1=0
(13)
式(13)化简结果为λDD=λD。根据表2中λDD=CdλD,而危险覆盖因子Cd<1,可知λDD<λD。
对于1oo2系统的六阶转移矩阵P,|λE-P|=0的特征值λ如式(14)和式(15)所示。
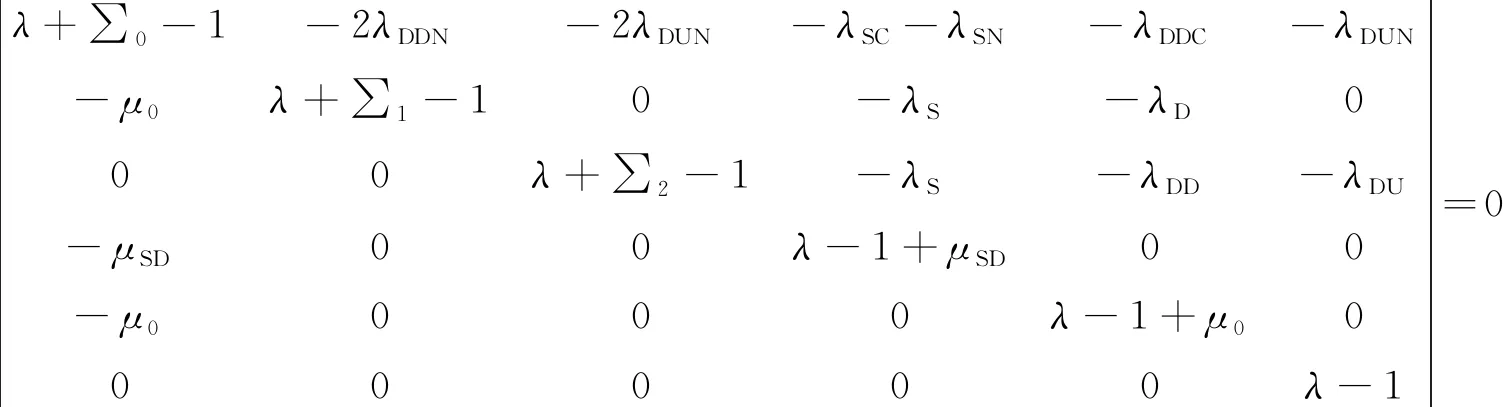
(14)
(15)
式中:∑0为第0行元素之和;∑1为平行元素之和;∑2为第2行元素之和。
为求证特征方程不存在特征值为1的重根,将λ=1代入式(15)中的行列式,化简得到特征多项式为:
Y=μ0μSD∑0∑1∑2-μ0μSD(2λDDNλD∑2+
2λDUNλDD∑1+∑2λDDC)
(16)
由表2可知:λDD<λD,λDDC<λD,λDDN<λD,λDUN<λD。因此,在λD<0.1时,式(16)可化简为:
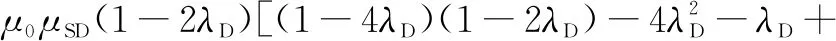
(17)
综上可知,特征方程式(12)、式(14)不存在值为1的重根,即λ1、λ2、λ3、λ4互异。
由此证得上述Markov状态转移矩阵P可相似对角化。
3 试验分析
3.1 天然气集气站安全仪表系统数据
试验采用四川地区某天然气集气站的安全仪表系统可靠性参数。该集气站共划分为15个安全仪表功能,分别执行火灾关断、进站高高压力切断、进站低低压力切断和污水系统低液位关断的安全功能。本次试验选取其中最具代表性的5个安全仪表功能。传感器、最终元件、逻辑单元的可靠性参数分别如表3、表4及表5所示。

表3 传感器的可靠性参数

表4 最终元件的可靠性参数
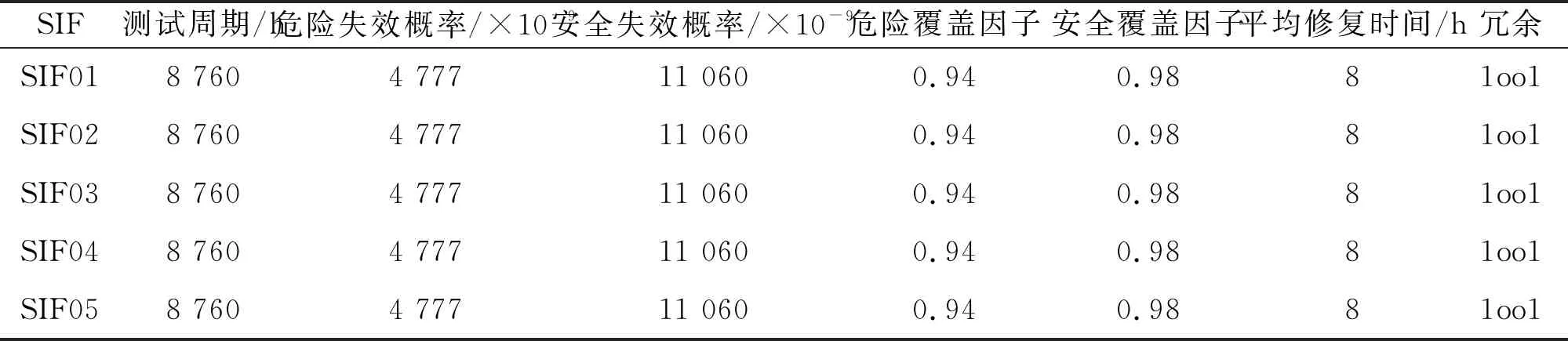
表5 逻辑单元的可靠性参数
3.2 两种方法结果对比
分别使用原始Markov模型法和R-Markov模型法计算5组SIF的平均要求时失效概率,分析比较两种方法花费的时间和计算结果。每组数据分别进行10次试验,时间取平均值。为消除干扰因素,只计算两种方法核心算法耗时,不考虑构建Markov转移矩阵等公共计算开销。两组试验均在相同软件、硬件环境下进行。两种方法计算结果如表6所示。
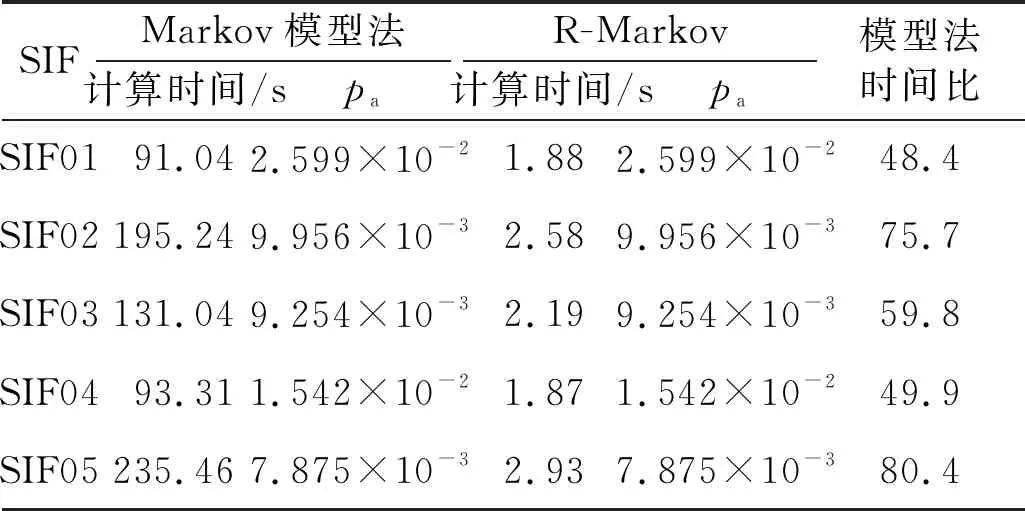
表6 两种方法计算结果
3.3 系统冗余度和测试周期T的影响
从式(6)、式(9)所示两种方法的计算复杂度可知,相比R-Markov模型法,Markov模型法耗时对转移矩阵阶数(即系统冗余度)和测试周期更为敏感。通过一组试验,分别验证系统冗余结构和测试周期对计算时间的影响。试验数据采用表3中SIF02的传感器可靠性参数,仅计算传感器的要求时失效概率。设定测试周期为8 760 h、13 140 h和17 520 h,分别在1oo1、1oo2、2oo3条件下进行运算。单元件运算结果对比如表7所示。冗余结构和测试时间对效率提升的影响如图3所示。

表7 单元件运算结果对比
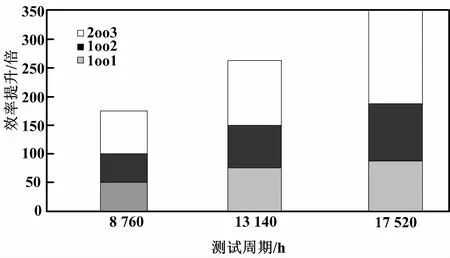
图3 冗余结构和测试时间对效率提升的影响
3.4 结果分析
分析表6、表7数据和图3可得如下结果。
①R-Markov模型法在5组SIF可靠性数据上提高约48~80倍效率。该计算结果和Markov模型法完全一致。
②结合表6中的时间比和表3~表5中各SIF回路的可靠性数据可知,SIF02、SIF03、SIF05中部分元件使用了更长的测试周期和更复杂的冗余结构,此时优化后算法的执行效率有更显著的提高。
③由表7和图3可知,Markov模型法计算效率对系统冗余结构和测试周期非常敏感,而R-Markov模型法的计算耗时始终能控制在非常低的水平。随着冗余结构和测试周期的提高,两者计算时间的比值也显著增加。当测试周期为一年时,R-Markov模型法在3种冗余结构上计算效率分别提高至51.1、51.9和77.2倍。当测试周期为一年半时,计算效率则提高至70.7、72.4和118.6倍。当测试周期为两年时,计算效率达到了91.5、94.6和164.3倍。随着测试周期的进一步增加,这一差距将会更加明显。
4 结论
本文在Markov模型法的基础上,提出了一种新的验算安全仪表系统SIL的方法,解决了Markov模型法计算量大、计算时间长的缺陷。通过数学原理,证明了该方法的可行性。本文采用真实天然气集气站的安全仪表系统可靠性数据进行了两组对比试验。试验结果表明,在不同的冗余结构和测试周期条件下,R-Markov模型法将SIL验算的计算效率提高了48~160倍。分析试验数据,R-Markov模型法即使用于大型复杂系统的SIL验算任务,最终运算时间也可控制在10 s内,为大型化工处理厂批量SIL验算工作提供了高效的解决方案。
