基于递推最小二乘法的仿人机械手控制技术研究

秦洪浪

(陕西工业职业技术学院航空工程学院，陕西 咸阳 712000)

0 引言

智能技术和传感控制技术是机器人研发制造的核心技术。机器人的智能化程度直接取决于核心技术水平的高低[1]。面对复杂的环境，机器人要完成一些具有难度的任务，需要对获取的信息进行综合分析和自主决策，这就意味着对机器人各种核心控制技术具有更高的要求[2-3]。现阶段我国机器人的控制技术虽已达到计算机智能层面，但在远程控制中还存在反应时间长和灵敏差等不足之处[4]。要实现机器人反应灵敏度和动作协调性的提高，需要不断对各种核心技术进行优化。

本文结合仿人机械手的设计原理，在对机械手进行动力学分析的基础上，研究、分析机械手的自抗扰控制技术和响应的算法优化，以提高机械手的整体控制精度。

1 仿人机械手动力控制技术研究

1.1 仿人机械手运动学分析

研究混合采用3D打印材料与铝合金707加工制作仿人机械手，组合使用谐波减速器和永磁同步电机，在保证机械手刚性的同时，兼顾机械手的精度[5]。机械手结构设计主要选用腱传动模式，动力驱动选用电机驱动[6]。基于腱传动原理，欠驱动手指各个指关节通过绳轮串联，牵引绳子即可控制手指的弯曲伸展。

选择合适的电机，在带动轮子转动的同时可起到牵引绳子的作用。电机主要根据功率大小、体积大小和响应速度等因素进行选择，其直径一般为6～14 mm。机械手指结构如图1所示。

图1 机械手指结构

驱动轮结构采用光敏树脂3D打印，钢丝绳通过其通孔可固定整个手掌结构[7]。整个手掌大小与真人手掌结构比例接近1∶1。手指指尖采用应变式薄膜压力传感器，压力检测范围为0～50 N，电阻变化范围为4 000～8 000 Ω。机械手指在不受外界阻力时，计算式如式(1)所示。

v0=w0R0

(1)

式中：v0为绳子速度；w0为电机减速后输出的轴转速；R0为动力轮半径。

假设手掌和手指连接部位的转动关节的速度为w1，其动力轮半径为R1，则w1为：

(2)

手掌和手指连接部位的转动部位相邻关节的转速分别用w2和w3表示，计算方法同w1。当手指碰到障碍物时，各个关节部位具有线性叠加的关系，如式(3)所示。

(3)

式中:R=R1=R2=R3。

将机械手臂结构进行简化处理，联合采用D-H参数法和坐标系后置的方式，可构建仿人机械手的运动学数学模型[8]。根据机械手结构，设置各D-H参数。

坐标后置各参数定义如图2所示。D-H参数值如表1所示。

图2 坐标后置参数定义

表1 D-H参数值

连杆坐标系从{i-1}到{i}，其齐次变换矩阵如式(4)所示。机械手臂的正向运动学求解可用式(5)表示。

(4)

(5)

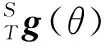
(6)

结合式(5)，可解得工具坐标系相对于惯性坐标系的位置表达式，如式(7)所示。

(7)

采用Robotics Toolbox 10.2.0确定六个关节间所形成的角度矢量。通过输入各关节角度，可得到机械手臂的三维空间姿态[9]。

1.2 自抗扰电机控制技术研究

本次研究的机械手驱动系统采用三相永磁同步电机(permanent magnet synchronous motor,PMSM)，忽略电机铁心饱和和磁滞、涡流造成的损耗，将相电流波看作对称的三相正弦波，对电机的数学分析模型进行简化[10-13]。三相永磁同步电机的电压方程式在ABC三相静止坐标系中，可用式(8)表示。

(8)

式中:u3s为电机三相绕组的电压；i3s为电机三相绕组电流；R为电机三相绕组的电阻；ψ3s为电机三相绕组的磁链。

三相永磁同步电机的电磁转矩方程如式(9)所示。

(9)

式中：Pn为电机的极对数；θm为电机的机械角度，rad。

三相永磁同步电机的机械运动方程如式(10)所示。

(10)

式中：TL为负载力矩,N·m；J为转动惯量,kg·m2；wm为机械转动角速度,rad/s；B为阻尼系数。

采用Clark变换将自然坐标系ABC变换成α-β静止坐标系。在α-β坐标系下，永磁同步电机的状态方程如式(11)所示。

(11)

式中：L为定子绕组电感,H。

为了便于设计控制器，研究选择两相同步旋转坐标系d-p轴下的三相永磁同步电机数学模型进行控制算法设计，主要采用Park转换，如式(12)所示。

(12)

在两相旋转坐标系中，永磁同步电机定子电压方程如式(13)所示。

(13)

式中：Ld、Lq为定子电感轴分量；ud、uq为定子电压轴分量；id、iq为定子电流轴分量；ψf为永磁磁链。

永磁同步电机的矩阵方程如式(14)所示。采用表贴式则存在Ld=Lq的关系，矩阵方程简化后得式(15)。

(14)

(15)

将ABC三相静止坐标系的相关变量变换到同步旋转d-p坐标轴下进行运算是磁场定向控制(field oriented control,FOC)的核心思想[14]。把永磁同步电机的数学模型等效看作是直流电机模型，其电流环采用比例积分(proportional integral,PI)控制器。永磁同步电机的电流环控制策略为id=0，通常采用MATLAB中的S函数编写永磁同步电机在同步旋转d-p轴下的数学模型。自抗扰控制(active disturbance rejection control,ADRC)算法主要针对不确定系统，不需要构建相应的运动数学模型[15]。自抗扰控制系统主要由非线性状态误差反馈、跟踪微分器和扩张状态观测器3个部分组成[16]。机械手自抗扰控制系统均具有惯性，无法实现阶跃信号的控制跟踪，系统输入阶跃信号还会在一定程度上限制最大加速度[17]。本研究采用离散跟踪器建立1个过渡过程，以解决这个问题。离散跟踪微分器的基本形式如式(16)所示。

(16)

式中：u为输入的目标控制信号；xn-1为当前时刻过滤的控制信号;xn为下一时刻过滤的控制信号,如果信号为位置输入，则xn为下一时刻的目标位置；vn-1为当前时刻的目标速度；vn为下一时刻的目标速度；h为积分步长；r为跟踪加速度；h0为滤波系数，不需要滤波时，设置为h0=h。

传统的线性ADRC控制不需要构建控制系统模型，各个参数具有易发生变动的特点。实际控制过程中产生的非线性摩擦和测量噪声会对整体的控制效果造成诸多不良影响。非线性ADRC系统中多且复杂的参数则会直接增加CPU的运行负担[18]。本研究基于对PMSM模型进行前馈，然后采用ADRC算法，以便于控制系统根据在线惯量识别结果完成系统参数的实时调整，从而保证整个电机控制系统的控制精确度和稳定性。因递推最小二乘法具有良好的稳定性，此次研究采用带遗忘因子的递推最小二乘(recursive least square,RLS)法实现控制系统的参数识别，主要识别惯量和阻尼系数2个参数。将参数识别结果和自抗扰算法结合使用，可提高整个机械手控制系统的适应性和控制稳定性[19]。最小二乘法作为1种数学优化技术，可通过最小化误差的平方和找到各个数据的最佳匹配，求得未知数据[20]。在机械手控制技术中，首先进行最小二乘法算法初始化处理。其处理过程如式(17)所示。

P(0)=δI∈CM×M

(17)

式中：δ为足够小的正数；I为单位矩阵，阶数为M×M。

取n=1,2,…,N，则迭代运算过程如式(18)所示。

(18)

更新n=n+1，进一步进行迭代运算。根据电机运动方程和电磁转矩方程，可简化计算得到式(19)。

iq=k1a+k2w+k3TL

(19)

式中：iq为q轴电流，由三相电流合成计算得到；a为电机的加速度；w为电机转速；TL为负载力矩;k1、k2、k3均为系数。

iq、a、w和TL四者存在线性叠加关系，可利用最小二乘法对系数进行最小方差估计。结合系数可分别计算得到系统惯量、阻尼系数和负载力矩的估计值。系统处于初始化状态时，各系数值均为0。因为初始时刻估计值误差较大，电机运行一段时间后才会收敛。所以先根据递推最小二乘法对静态空载下的电机进行系统辨识，把辨识得到的参数写入FLASH；再把电机装入执行关节，对其进行控制。

2 电机自抗扰控制试验

此次研究的电机自抗扰控制试验由4个不同的试验组成；一是电机抗外界干扰试验；二是低速转矩脉动抑制试验；三是在线参数辨识试验；四是位置动态控制试验。所有试验均使用MAXON ECI-40-50W电机。电机抗外部干扰试验的具体过程如下：首先，使电机处于空载状态，并锁定于当前位置；随后，将控制系统的带宽升高至800 rad/s，设定电机的最大输出电流的波动幅度为±3 A，并在电机轴上加入外界干扰力矩。

电机抗外界干扰试验结果如图3所示。

由图3可知，1 s内总共包含2 049个采样点。加入外界干扰力矩之后，电流峰值达到1.5 A。最大位移控制误差为6个脉冲，角度表示为0.526°。电机控制的位置稳态误差为±20个脉冲，控制角度误差为0.017 58°。将减速器的减速比设置成100，电机控制角度误差显示为0.005 26°。通过查询相应的参数手册可得到减速器的角度传达精度，结合机械手设计结构的相关参数值，可计算得到机械手的控制位置精度。X轴的控制精度为0.543 0 mm，Y轴和Z轴分别为0.490 86 mm和0.513 08 mm，各数值均小于1 mm，满足精度要求。

图3 电机抗外界干扰试验结果

设置转速的目标为5 rad/min，则低速转矩脉动抑制试验结果如图4所示。

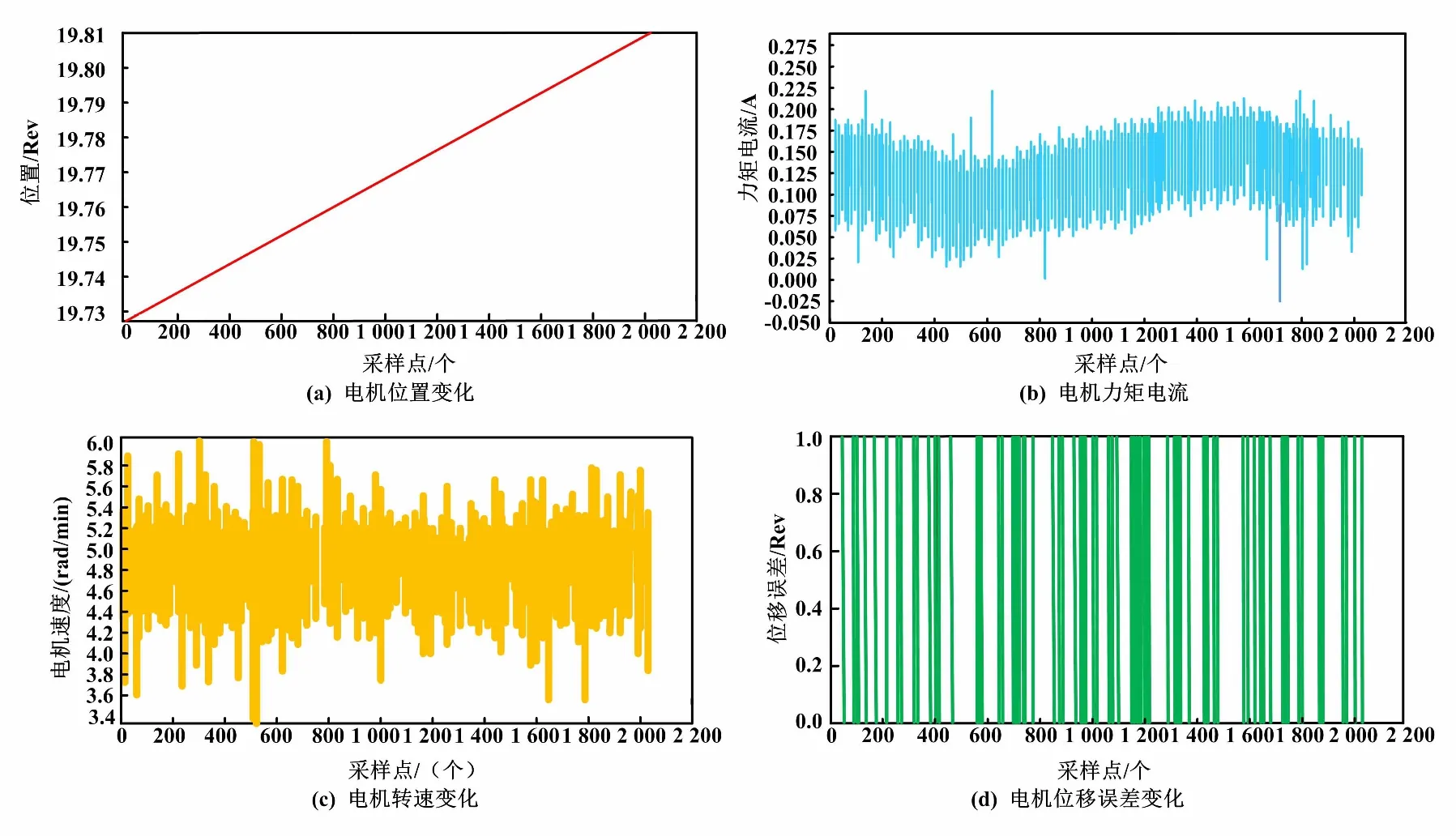
图4 低速转矩脉动抑制试验结果

由图4(a)可知，将匀速状态下的电机控制看作位置和时间的正相关函数，电机位置控制误差为1个脉冲。由图4(b)可知，为了抵抗低速条件下转矩的非线性摩擦，电流整体呈现出波浪形的状态。究其原因，可能是低速下编码器的离散误差致使速度观测器的速度估算出现不准确的现象，使位置控制出现误差。因此，可根据位置控制误差推导出速度控制误差范围值。

基于递推最小二乘法的惯量识别响应曲线如图5所示。

图5 惯量识别响应曲线

由图5可知，在0.7 s左右，实际惯量为初始惯量的10倍。实际值与真实值接近，此时的稳态误差为1×10-7kg/m2。

设置电机电流激励幅值为额定电流的30%，在3个不同测试周期内不断进行在线识别，所得的在线参数辨识试验结果如图6所示。

图6 在线参数辨识试验结果

由图6可知，上述惯量和阻尼参数适用于机械手的自抗扰控制系统。进一步就辨识结果对速度控制和位置控制进行准确度验证，发现自抗扰算法虽然不依赖参数，但通过参数识别可提高控制系统整体的控制精度。

在位置动态控制试验中，设置正弦位置目标信号的角频率为80 rad/s，幅值设为0.015圈。位置动态控制响应曲线和误差曲线如图7所示。

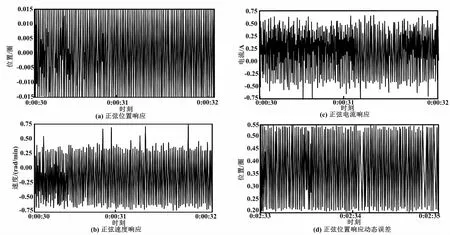
图7 位置动态控制响应曲线和误差曲线

分析图7(a)～图7(c)，不同位置控制响应值分别用圈数、rad/min和A三种单位形式表示。图7(d)为正弦位置响应动态误差随时间变化的曲线。由图7可知，在基于递推二乘法的自抗扰算法的机械手控制数学模型中，在电流控制和采样频率均为20 kHz的条件下，位置动态响应误差可控制在±20脉冲内。

3 结论

仿人机械手控制精度的提高对机器人智能化发展有着至关重要的作用。因此，本文研究在对机械手设计原理和动力学进行分析的基础上，为提高机械手控制精度和灵敏度，对机械手设计中的电机自抗扰控制技术进行研究分析，并引入带有遗忘因子的递推二乘法对电机数学模型的惯量和阻尼系数进行识别，进而实现控制算法的优化。分别对机械手的力矩、速度和位置控制进行性能测试。结果显示，电流控制频率达到20 kHz时，位置动态响应误差可控制在±20脉冲内。该研究表明，引入带有遗忘因子的递推二乘法有助于提高机械手的整体自抗扰控制技术水平。提高机械手的自主反应速度和灵敏度依然是下一步研究的主要方向。