金属壳体振动陀螺的多参数温度补偿技术研究
2021-10-09张勇猛郭锞琛吴宇列
张勇猛,郭锞琛,席 翔,吴宇列
(国防科技大学智能科学学院,湖南 长沙 410073)
0 引言
金属壳体振动陀螺是一种利用壳体弹性波惯性效应测量载体角速度的传感器,具有结构简单、精度高、体积小、可靠性高、寿命长等显著优势,在军用和民用领域都有广阔的应用前景[1-2]。西方发达国家对高精度陀螺仪实施严格的禁运政策。因此,掌握金属壳体振动陀螺的核心技术、提升陀螺精度具有重要意义。
陀螺的温度漂移是指陀螺的输出随着环境温度的变化而出现的趋势性变化。金属壳体振动陀螺的温度漂移是目前制约金属壳体振动陀螺工程化应用的主要因素,也是振动类陀螺普遍面临的重要难题。
温度补偿是提高陀螺温度稳定性的常用方法。国内外许多学者对此进行了研究。研究重点集中在陀螺零偏温度模型的建立。研究人员先后提出了采用线性回归[3-4]、神经网络[5]、模糊算法[6]等多种方法建立模型,对陀螺输出进行补偿。采用零偏温度模型进行时补偿时存在的主要问题是温度的滞回效应。其原因是温度传感器测量的温度与陀螺的真实温度之间不可避免地存在一定的迟滞。
为了克服滞回效应,半球谐振陀螺的研究人员提出了基于零偏频率模型的温度补偿方法[7]。谐振子的谐振频率与温度具有良好的对应关系。因此,可以把谐振子的谐振频率作为补偿基准,建立陀螺输出与频率的数学模型,对陀螺输出进行补偿。由于谐振频率是谐振子本身的固有属性,可以实时反映谐振子本身的温度状态,所以基于零偏频率模型的补偿方法可以有效地减小温度滞回效应的影响,提高温度补偿的精度。
但金属壳体振动陀螺与半球谐振陀螺在驱动和检测方式上存在巨大差异。金属壳体振动陀螺采用压电电极进行驱动和检测。这是一种接触式的驱动检测方法。压电驱动和压电检测具有信噪比高、无需镀膜、工艺简单等优势[8-9],但同时也引入了电极的粘贴误差,例如电极粘贴位置误差以及胶层参数不一致带来的增益误差等。这些误差都会对陀螺的零偏稳定性产生影响。接触式的驱动和检测方法使得金属壳体振动陀螺的零偏输出与谐振子的真实温度之间的重复性变差。采用零偏频率模型进行补偿后的金属壳体振动陀螺仍然存在着不小的温度漂移。
由此可见,采用单一参数对金属壳体振动陀螺进行温度补偿很难取得满意的效果。本文拟采用多参数模型进行温度补偿,以减小温度滞回和压电电极增益不重复引起的零偏漂移。
1 金属壳体振动陀螺的零偏漂移分析
1.1 工作原理
金属壳体振动陀螺谐振子的基本结构如图1所示。

图1 金属壳体振动陀螺谐振子的基本结构
其核心部件是一个具有圆柱壳结构的谐振子,主要由谐振结构、导振结构以及支撑结构三大部分组成。谐振结构是谐振子上壁厚较厚的圆环,是谐振子的主要敏感质量;导振结构是指谐振环下面的壁厚较薄的圆环以及圆盘形的底部;支撑结构是指谐振子底部的安装杆,谐振子通过它固定在底座上。
在谐振子的底部,贴有8片均匀分布的压电电极作为谐振子的驱动和检测部件。谐振子采用高稳定性的弹性合金材料制成,其主要加工工艺是车削。精加工完毕的谐振子仍不可避免地存在材料非均匀与几何误差。为了提高谐振子的均匀性,一般采用在谐振环上刻槽或者打孔的方法对谐振子进行精密修调。
金属壳体振动陀螺检测角速度的理论基础是哥氏加速度。哥氏加速度由法国人科里奥利于1835年提出,是由动参系的转动与动点相对动参系运动相互耦合引起的加速度[10]。在谐振子的驱动电极上施加正弦驱动信号,信号的频率等于谐振子四波腹振型的固有频率,激励出谐振子的驱动模态。
当谐振子敏感轴向有角速度输入时,谐振子上振动的各微元受到哥氏力的作用。哥氏力的方向可由右手法则确定,大小与振动的速度和输入的角速度成正比。金属壳体振动陀螺的工作原理如图2所示。

图2 金属壳体振动陀螺的工作原理
由图2可知,哥氏力的合力沿45°方向,激励出了谐振子的敏感模态。敏感模态振动的幅值与输入角速度的大小成正比,通过解调敏感模态的振动,就可得到角速度的大小。
1.2 动力学模型
圆柱壳体谐振子可以等效为一个二维振荡系统[11]。谐振子的等效二维振荡模型如图3所示。图3中,X、Y为谐振子坐标系。由于谐振子的两个固有刚性轴间隔45°,所以从模态振型的角度来说,X、Y是正交的,θω为刚性轴与X轴的夹角。x、y为二维振荡模型中的固定坐标系,x′、y′为二维振动系统的固有模态刚性轴,2θω是谐振频率为ω1的刚性轴与x轴的夹角。

图3 谐振子的等效二维振荡模型
利用类似的方法,考虑谐振结构的阻尼不均匀误差,令谐振结构衰减时间常数的两个极值分别为τ1、τ2,衰减时间常数为τ1的阻尼轴与x轴的夹角为θτ。
根据美国学者Lynch的理论[12],金属壳体振动陀螺二维振荡模型的运动方程可写为:
(1)
式中:k为谐振结构的运动系数;Ω为输入的角速度;c11为x轴的阻尼系数;c12为x轴耦合到y轴的阻尼系数;c21为y轴耦合到x轴的阻尼系数;c22为y轴的阻尼系数;k11为x轴的刚度系数;k12为x轴耦合到y轴的刚度系数;k21为y轴耦合到x轴的刚度系数;k22为y轴的刚度系数。
上述变量可表示为:
(2)
式(2)中:
(3)
式中:ω1、ω2为谐振结构在两个固有刚性轴方向的固有频率。
谐振子的二维振荡模型考虑了谐振子的频率不均匀、阻尼不均匀以及两个模态之间的阻尼和刚度的耦合作用,对于研究金属壳体振动陀螺的性能具有重要的作用。本文将主要基于此模型研究金属壳体振动陀螺的零偏漂移机理和抑制方法。
1.3 力反馈模式下的零偏漂移机理
金属壳体振动陀螺具有全对称的谐振结构,其驱动模态和检测模态理论上具有相同的谐振频率。因此,在开环模式下,陀螺的量程小、带宽低、线性度差。为了提高陀螺的量程、带宽和线性度,金属壳体振动陀螺通常在力反馈模式下工作。
在力反馈模式下,控制电路通过输出反馈力将谐振子的敏感模态振动抑制为零,从反馈力中解调得到陀螺的角速度。
谐振子在x轴上维持恒幅振动,其振动位移为:
x=Axsinωxt
(4)
式中:Ax为谐振子驱动模态的振动幅值;ωx为陀螺的工作角频率。
将式(4)代入y轴的振动方程中,可得:

k12Axsinωxt
(5)
在力反馈模式下,反馈力Fy使得谐振子在y轴上的响应抑制到0。因此,令式(5)右边等于零,可得反馈力Fy的表达式如下:
Fy=(4kΩ+c12)Axωxcosωxt+k12Axsinωxt
(6)
陀螺的输入角速度可以通过对反馈力Fy用余弦信号作基准解调得到。解调后陀螺的输出为:
(7)

Scloseloop=4kAxωx
(8)
力反馈模式下的零偏输出为:
(9)
式中:Q1、Q2分别为谐振结构在两个固有阻尼轴方向的品质因数(Q值)。
由此可见,在力反馈模式下,陀螺的零偏输出中与频率裂解有关的误差已经被消除了。陀螺的零偏漂移仅与谐振子的阻尼不均匀和阻尼轴方位角有关。通过增大谐振子的Q值,可以减小阻尼不均匀引起的零偏漂移。
2 零偏漂移的补偿参数选择
根据上文对金属壳体振动陀螺闭环模式下的零偏漂移分析,可知引起金属壳体振动陀螺温度漂移的原因主要有:频率裂解、刚性轴旋转、阻尼不均匀、阻尼轴旋转以及谐振子增益的改变。金属壳体振动陀螺的温度补偿参数可以从与这些影响因素相关的电信号中选取。此外,被选作补偿参数的信号还要与陀螺的角速度无关,否则会影响陀螺输出的线性度。
2.1 正交反馈量
当不考虑陀螺测控电路的相位误差时,频率裂解和刚性轴旋转引起的温度漂移可以被力反馈电路抑制。但是,测控电路不可避免地会存在一定的相位误差。此时,频率裂解和刚性轴旋转仍会引起陀螺的零偏漂移。存在相位误差时,频率裂解引起的漂移项为:
(10)
式中:δps为检测环路的相位误差。
此时,测控电路正交回路的反馈量为:
(11)
由此可见,正交反馈量和频率裂解引起的零偏漂移项具有相同的形式,因此可以把正交反馈量作为参考信号,以补偿频率裂解和刚性轴旋转引起的零偏漂移。
2.2 温度
不考虑刚性轴的旋转和频率裂解,当阻尼不均匀变化或者阻尼轴旋转时,金属壳体振动陀螺的零偏输出也会产生漂移。因此,在陀螺测控电路的内部信号中,没有能直接反映谐振子阻尼的信号。但是,谐振子的Q值一般与温度具有良好的对应关系,因此可以以温度为参考信号补偿阻尼不均匀变化和阻尼轴旋转引起的漂移。
2.3 驱动电压
压电电极增益误差也是引起金属壳体振动陀螺温度漂移的一个重要原因。由于压电驱动是一种接触式的驱动方式,升降温过程中电极和胶层的增益存在一定的不重复性,采用温度作为补偿参数很难消除这类非重复漂移。金属壳体振动陀螺有两个基本模态。温度的变化不仅会引起敏感模态压电电极的增益误差,也会引起驱动模态压电电极的增益误差,由于驱动模态和敏感模态的电极采用的是相同的材料和粘贴工艺,温度变化对其增益造成的影响也是基本一致的。因此,本文选取驱动模态的驱动幅值控制信号作为补偿参数。该信号的大小与驱动电压的幅值成正比,可以用于补偿压电电极增益误差引起的温度漂移。
综合以上分析,本文对金属壳体振动陀螺进行温度补偿参数的选择如图4所示。
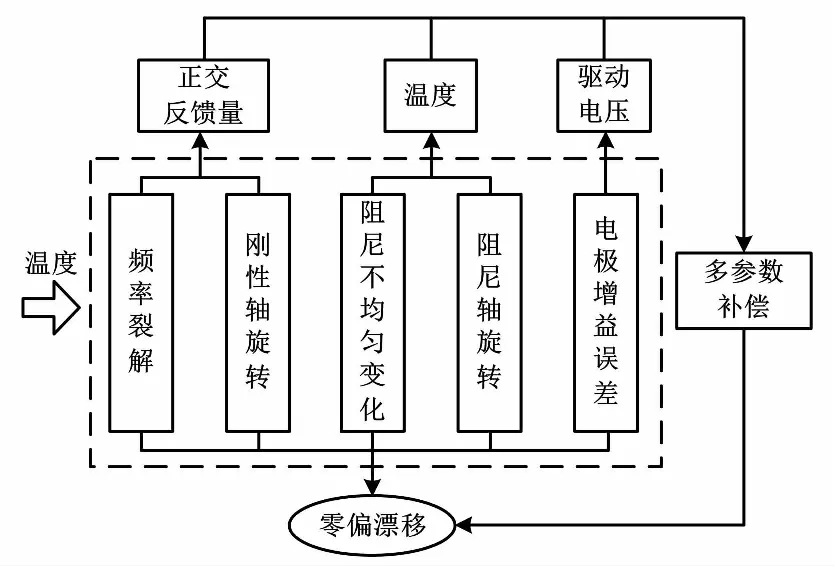
图4 温度补偿参数的选择
利用正交反馈量对频率裂解和刚性轴旋转引起的温度漂移进行补偿;利用温度对阻尼不均匀变化和阻尼轴旋转引起的温度漂移进行补偿;利用驱动模态的驱动电压幅值对压电电极增益误差引起的温度漂移进行补偿。与仅用温度参数进行补偿的方法相比,多参数补偿方法从机理上可以消除大部分温度滞回效应引起的残余漂移。
3 零偏漂移的多参数温度补偿与测试
金属壳体振动陀螺的温度补偿电路主要实现以下功能:补偿参数的采集、补偿量的计算及补偿电压的输出。因此,补偿系统需要包括测量温度的传感器、采集数据的A/D转换模块、计算补偿量的微控制器模块,以及将数字补偿量转化为电压输出的模块。
温度补偿的过程如下:首先,对金属壳体振动陀螺进行温度测试。此时单片机不计算补偿量,而是直接将采集到的数据发送至上位机。然后,在上位机上利用优化算法得到陀螺零偏漂移的多参数模型。最后,上位机通过编程接口将模型烧写至单片机。
3.1 金属壳体振动陀螺的全温区测试
将金属壳体振动陀螺放入温控箱中,温控箱内的温度变化过程如图5所示。
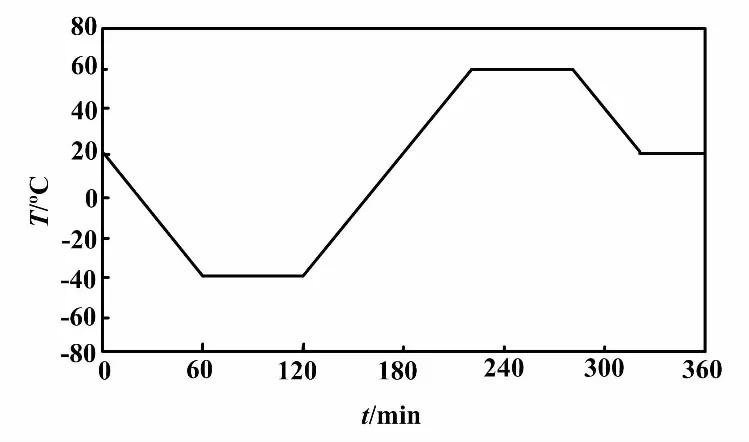
图5 温度变化过程
图5中,温度变化速率为1 ℃/min。
对金属壳体振动陀螺进行全温区测试的目的是得到建立温度模型所需要的数据。金属壳体振动陀螺的工作温度范围为-40~+60 ℃。
在温度试验过程中,金属壳体振动陀螺的温度补偿单片机将采集到的温度、驱动电压、正交电压以及陀螺零偏输出等数据通过串口发送至上位机采集软件。金属壳体振动陀螺的全温区测试数据如图6所示。

图6 金属壳体振动陀螺的全温区测试数据
3.2 补偿模型的建立
建立高精度的温度补偿模型是对金属壳体振动陀螺进行温度补偿的关键环节。模型的好坏直接决定了温度补偿的效果。本文采用多参数模型进行补偿。建模的过程本质上是一个多参数优化的过程。多参数模型具有多种形式。考虑到模型的可行性和实用性,本文采用多项式模型进行多参数温度补偿。多项式模型的具体形式为:
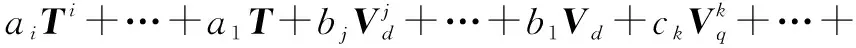
c1Vq+β0
(12)
式中:B为陀螺的零偏输出;T为陀螺温度;Vd为驱动电压;Vq为正交电压;i、j、k分别为三者的阶数;a、b、c为模型系数;β0为常数项。
模型的阶次越高,即i、j、k的值越大,模型的精度就越高,但在实际应用中还要考虑数字芯片的处理能力。若模型的阶次过高,运算的速度会减慢,影响补偿的实时性。系数a、b、c可以通过最小二乘法来进行拟合,得到其具体数值。
令:
则式(12)可写为:
B=Xβ+ε
(13)
式中:ε为随机误差。
(14)
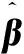
模型的性能评价函数为模型残差的平方和,即:
(15)
式中:n为待估计参数的个数,即向量β的维数;N为采集样本的容量,一般情况下N≫n。
将式(13)代入式(15),得:
J=εTε=(B-Xβ)T(B-Xβ)=
BTB-βTXTB-BTXβ+βTXTXβ
(16)
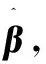
(17)
因此,最小二乘估计的一般形式为:
(18)
取N个温度点的采样数据作为建模数据,得到如下矩阵:
(19)
将式(19)代入式(18),即可求解各系数的最小二乘估计值,进而得到陀螺的零偏模型。
式(12)只是金属壳体振动陀螺多参数多项式模型的基本形式,具体各个变量的阶次和系数需要根据试验测试结果来确定最优形式。
3.3 金属壳体振动陀螺的补偿测试
根据求得的金属壳体振动陀螺零偏多参数模型编写温度补偿程序,然后对补偿后的陀螺进行全温区测试,得到其全温区的零偏输出。由此可知,经过多参数温度补偿后,金属壳体振动陀螺的全温区零偏稳定性得到了显著提升。
多参数温度补偿后的陀螺全温区输出如图7所示。

图7 多参数温度补偿后的陀螺全温区输出
测试用的金属壳体振动陀螺的标度因数为60 mV·s/(°),多参数温度补偿与传统温度补偿的对比如图8所示。在全温区的升降温过程中,金属壳体振动陀螺补偿前的最大漂移量为300(°)/h,多参数温度补偿后的最大漂移量在10(°)/h以内,减小至补偿前的3.3%。若只采用温度数据对金属壳体振动陀螺进行补偿,补偿后陀螺在全温区的最大漂移量为35(°)/h。由此可见,多参数温度补偿方法的补偿效果优于传统温度补偿方法。

图8 多参数温度补偿与传统温度补偿的对比
4 结论
本文主要针对金属壳体振动陀螺的全温区零偏稳定性进行了温度补偿。首先,对金属壳体振动陀螺零偏漂移机理进行分析,提出了基于正交反馈量、温度、驱动电压的多参数温度补偿方法。这三个补偿参数分别对应频率裂解和刚性轴旋转、阻尼不均匀变化和阻尼轴旋转、压电电极增益误差引起的温度漂移。利用试验测试数据,建立了多参数模型,设计了温度补偿电路。最后,对金属壳体振动陀螺的常温和全温区零偏稳定性进行了测试。补偿后的全温区最大漂移量在10(°)/h以内,减小至补偿前的3.3%。
