基于模型分析的健康监测振动测点布置分析

许亮，邹云华，冯俊

（1.湖北省交通运输厅公路管理局，武汉430030；2.湖北交投智能检测股份有限公司，武汉430050）

1 引言

长江大桥由于其修长且具有柔性的结构形式，导致结构主要振型模态频率值较低，极易与风、地震、车辆等外部荷载作用产生耦合振动效应，从而给桥梁结构带来损伤，并且影响桥梁的安全正常运营。作为大桥运营期间主要的检测手段，健康监测系统对于桥梁正常或异常状态的判断分析起到了至关重要的作用。本文采用模态置信准则（MAC）评价石首长江公路大桥振动传感器的配置和优化。

2 振动传感器优化布置原则

基于有限元分析结果，桥梁结构各固有振型在测点位置的振型值便形成了多组相互正交的向量，其与质量矩阵和刚度矩阵正交。但由于振动测点布置数量远小于结构实际自由度，且传感器测试存在精度及噪声影响，实测模态向量不一定正交，极有可能出现由于模态向量空间夹角偏小而丢失或错误分析重要模态的情况[1]。因此，振动测点布置应使各阶模态向量保持较大的空间角，即保证各模态向量最大可能不相似。

目前，桥梁振动传感多以均匀布置为主，并不能保证各主振型向量间拥有较大空间角，国外一些学者认为模态置信准则（MAC）是评价振型模态向量空间角较好的工具，可用于传感器的优化布置。模态置信准则（MAC）表达式为：

式中，MACij为αi、αj2个模态向量的模态置信准则的值；αi、αj分别表示桥梁第i阶、第j阶振型模态在相同测点处的振型模态向量；αiT为αi的转置向量。MACij取值范围为0≤MACij≤1。当MACij=0时，表明向量αi、αj的空间交角为90°，即2个振型向量线性无关，容易分辨；MACij=1（i=j）时，表明向量αi、αj的空间交角为0°，2个振型向量线性相关，不能分辨；0＜MACij＜1时，2个振型向量相关性介于二者之间。所以，振动测点的布置应该使MAC矩阵非对角元素最小化。

根据规范要求，桥梁结构整体响应测点布置选择应根据结构动力计算结果、振型特点及所需的监测振型阶数综合确定，振动传感器宜布设在结构主要振型最大振幅或较大部位。对感兴趣的m阶振型选出n个测试自由度布置测点，每个测试自由度对应有限元模型中的相应节点位置，以φnm表示n个测点自由度形成的m阶模态向量矩阵。则m阶振型向量的MAC矩阵可表示为：

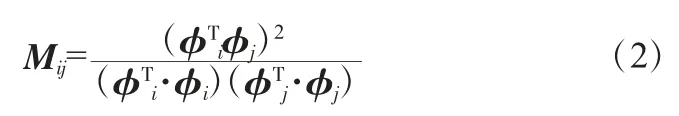
式中，φi、φj分别表示第i阶、j阶模态振型在n个测点处的振型向量（1≤i≤m，1≤j≤m）。Mij的取值范围为0≤Mij≤1。假设Hmm=φTmm×φmm，hij为矩阵Hmm的第i行、j列元素值,则式（2）可变换为：

进行振动测点优化的过程就是添加或删减测试自由度的过程。根据优化方式不同，存在3种优化形式：

1）增加测试自由度数量；

2）在特定测试自由度数量下优化测点布置；

3）基于有限元模型重新优化。

为了使MAC矩阵非对角元素均值或最大值趋于最小化，每次增加（减少）1个振动测点，相当于每次在矩阵φ中增加（减少）1个测试自由度Ψk=[φk1，φk2，…，φkm][Ψk为由于增加或减少1个振动测点，φnm向量矩阵对应增加或减少的1个行向量；φkm为增加或减少的1个行向量的最后1个元素值。增加时，k为结构当前剩余可选的测试自由度（例如，向量矩阵增加一个测点时，而剩余可布置测点的节点数为p，则n＜k≤n+p）；减少时，k为结构当前已选择的测试自由度（例如，向量矩阵减少一个测点时，1≤k≤n），即在原矩阵φ中增加（减少）1行元素值]。当增加（减少）1个自由度时,可得新的MAC矩阵元素[2，3]为[式（4）表示增加，式（5）表示减少]：

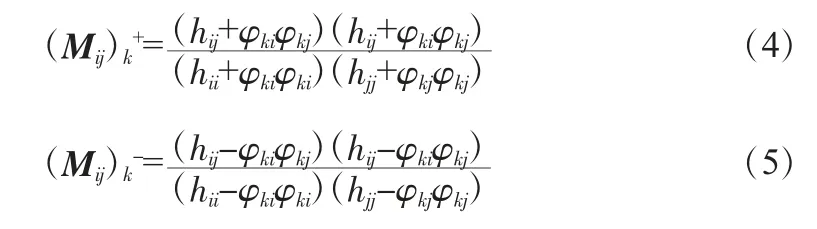
式中，φki、φkj分别为Φnm增加（减少）一个自由度后变成的矩阵Φ（n+1）m[Φ（n-1）m]的第n+1（n-1）行第i列和第j列元素值。

测点优化计算时，将其他可选的测点自由度逐一代入式（4）或（5）进行迭代计算，可得到对应个数的新MAC矩阵，比较各新矩阵非对角元素最大值与原矩阵的大小，取最大值最小的MAC矩阵作为此轮迭代计算成果。重复此步骤，直到所得新的MAC矩阵非对角元素值小于预期值为止。通过VBA编程分别计算增加测试自由度数量、保持测试自由度数量不变以及基于有限元模型选择初始测试自由度3种优化布置方案。

3 石首长江公路大桥有限元模型

石首长江公路大桥桥跨布置为（75 m+75 m+75 m）+820 m+（300 m+100 m），钢混结合面位于北塔附近，并伸入主跨距北塔中心线26.5 m；北边跨采用混凝土主梁，长251.5 m；主跨和南边跨采用钢主梁，全长1 193.5 m。主桥采用MIDAS Civil软件模拟计算，全桥离散为1 174个节点，957个单元，其中，主梁节点编号为1#～565#。边界条件：过渡墩、辅助墩位置均为纵向活动，竖向约束，过渡墩的球型支座具有横向限位功能，索塔位置设置横向抗风支座；索塔塔底和基础采用固结；斜拉索与主梁采用刚臂连接；索塔位置纵向阻尼器未安装。大桥有限元分析模型如图1所示。

图1 大桥有限元分析模型

大桥健康监测系统[4]关注的主梁主振型为前10阶，包括1阶纵飘振型、6阶竖弯振型以及3阶侧弯振型。本文主要研究竖弯振型测点布置，辅以侧弯振型进行验证。

为方便布置及统一管理，大桥健康监测系统振动测点均匀布置在各跨等分点及主跨最大挠度处，振动测试自由度布置在节点298#、360#、404#、498#和518#处，测试自由度所在节点布置如图2所示，方案对应的MAC矩阵非对角元素最大值为0.646 5，第7、8阶与第10阶振型向量相似度较高，实测时难以分辨。

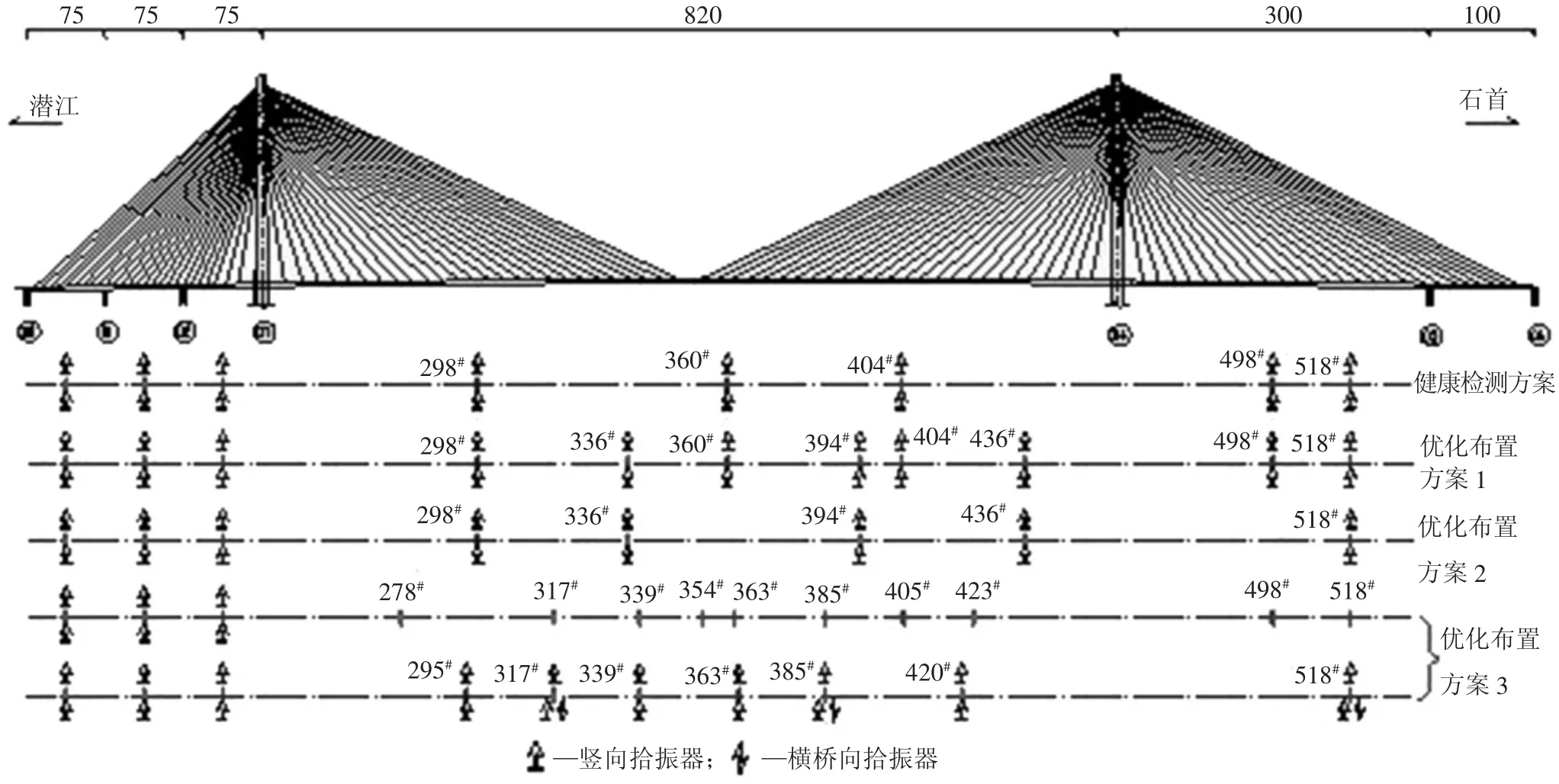
图2 大桥振动测点优化布置汇总图

4 振动测点布置优化分析

如前文所述，模态置信准则（MAC）没有正交性检查严格，其不需要考虑结构质量或刚度矩阵，适用于质量或刚度分布较均匀的桥梁或桥跨。石首长江公路大桥北边跨混凝土梁段的质量及刚度均大于钢箱梁桥跨，振幅较大值集中在跨中部位，在各跨跨中布置竖向传感器即可。针对大桥主跨及南边跨，振动传感器布置可以采用如下4种方式优化。

4.1 增加测试自由度数量的测点优化布置

选取主梁剩余可布置传感器的节点进行迭代计算，迭代计算的MAC矩阵最大值变化曲线如图3所示。当选取8个测试自由度，曲线变化趋于平缓时，矩阵非对角元素最大值减小为0.083 4，达到预期效果。

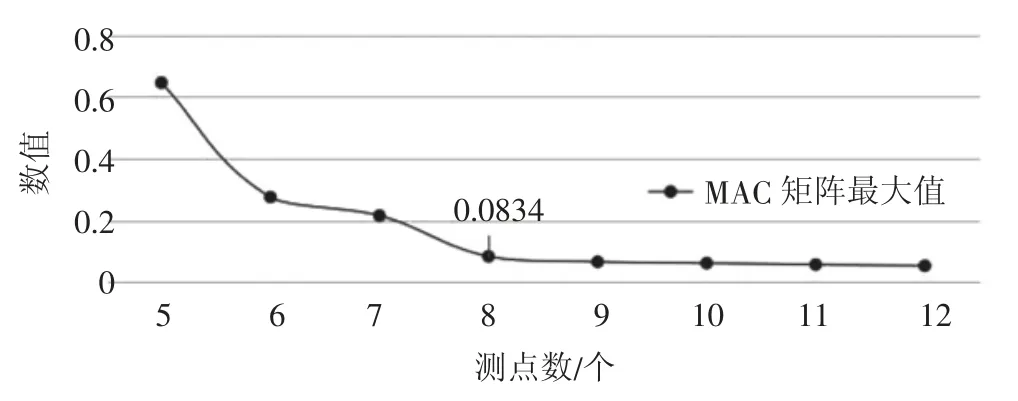
图3 增加测试自由时MAC矩阵非对角元素最大值变化规律图

4.2 特定测试自由度数量下的测点优化布置

考虑加入相比健康监测方案更为优化的测试自由度，将原有测试自由度增加到12个，在此基础上进行删减迭代优化，迭代计算的MAC矩阵最大值变化趋势如图4所示。程序最后优化至5个测试自由度，分别在节点298#、336#、394#、436#及518#节点处，此时，矩阵非对角元素最大值为0.199 0，相比原有方案替换了3个测试自由度，说明原均匀布置方案尚可进一步优化。

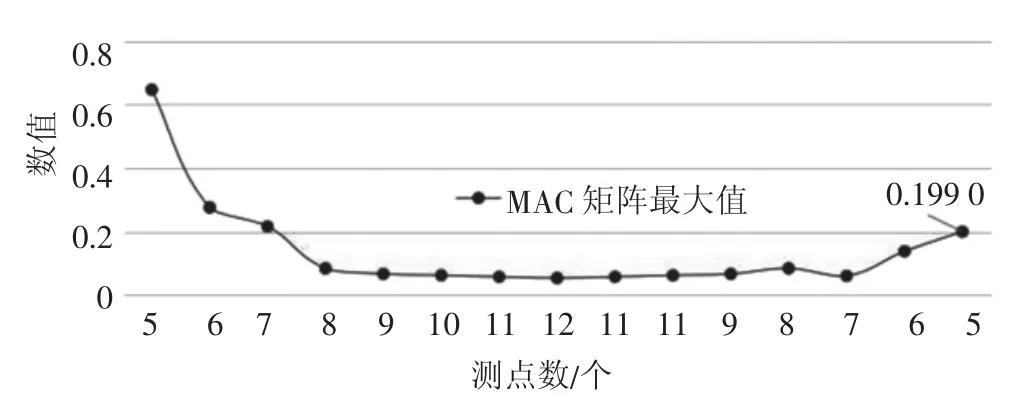
图4 优化测点布置位置时MAC矩阵非对角元素最大值变化规律图

4.3 基于模型初始测试自由度选择的测点优化布置

以有限元分析模型为基础，在竖向主振型振幅最大或较大位置设置测试自由度，本文初始选择10个测试自由度，分别 位 于278#、317#、339#、354#、363#、385#、405#、423#、498#、518#节点处，同时，避免遗漏更为优化的节点位置，利用计算程序将初始测试自由度迭代增加至14个。在初始14个测试自由度基础上，进行多次删减迭代计算，迭代计算的MAC矩阵最大值变化曲线如图5所示。当测试自由度为7个时，曲线到达上升拐点处，此时矩阵非对角元素最大值减小为0.058 4，达到预期效果，各测试自由度所在节点位置如前述图2所示。

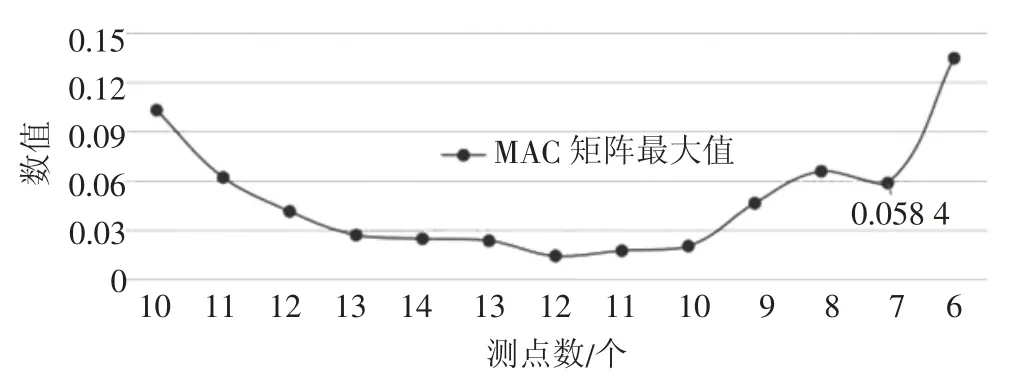
图5 基于模型计算选择和优化测试自由度时MAC矩阵非对角元素最大值变化趋势图

对比以上优化方案，选择基于模型初始测点选择的优化方案在测试自由度数量及MAC矩阵上都较为合理，适用于测点的重新布置。

4.4 侧弯振型测点优化布置

以基于模型初始测试自由度选择的优化方案为基础，进行横桥向振型实测自由度删减迭代计算，经程序计算最终优化至3个测试自由度，分别在317#、385#及518#节点处，此时的MAC矩阵非对角元素最大值为0.002 3。

利用模态置信准则（MAC）进行振型测点优化过程中的结论如下：（1）不同节点对MAC矩阵非对角元素的削弱能力不同，削弱能力大的节点，增加节点时程序会优先考虑，削弱能力小的节点，减少节点时程序会优先考虑。（2）迭代计算时，振幅较小的节点对MAC矩阵非对角元素影响较小，迭代计算时程序增加的节点集中分布于主跨跨中振幅较大的部位，这刚好与初始节点选择的初衷一致。（3）采用基于有限元模型等方法选择的初始节点，建议利用计算程序扩充到足够数量后再进行删减优化，避免初始节点选择产生遗漏。

5 结语

本文基于模态置信准则（MAC）对石首长江公路大桥健康监测振动测点进行了分析和优化布置，指出了原有均匀布置方式的不足，同时提出了3种测点优化布置方案，相比在特定测试自由度数量下进行测点优化，增加为数不多的测试自由度能带来显而易见的效果。对于本桥已建成的健康监测系统，增加3个测试断面，从经济性和实用性考虑是个较好的优化方案。