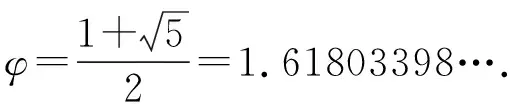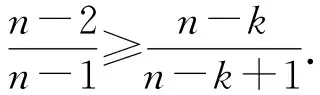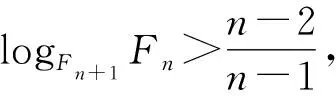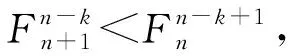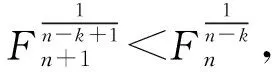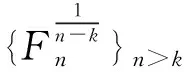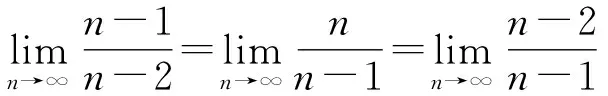对数的比较与斐波那契数列
——从2020年全国Ⅲ卷理科第12题谈起
2021-10-08肖志军
肖志军 张 浩
(1. 北京工业大学附属中学 100022; 2. 北京市朝阳区教育研究中心 100021)
1 一道“致命问题”
2020年全国Ⅲ卷理科第12题是一道比较对数大小的题目:已知55<84,134<85.设a=log53,b=log85,c=log138,则( ).
(A)a (C)b 解析因为34<53,所以4log53<3, 这样的问题曾被选为“致命问题”.美国麻省理工学院的数学家Tanya Khovanova及其Alexey Radul在2012年《美国数学月刊》第十期上合作发表文章《致命问题》(Killer Problems)[1],其中介绍的第11个问题是一个与上述题目类似的问题:log23与log35谁更大? 这篇文章的第一作者Khovanova曾于1976年代表苏联参加国际数学奥林匹克竞赛(IMO)获得金牌,并且是IMO有史以来第二位获得金牌的女选手.这篇文章包含了14道“致命问题”,王淑红和蒋迅[2]在《数学文化》上也介绍过这些问题,它们的特点是“构思新颖、设计巧妙,很难使人想到答案,但是一旦看到答案,又使人恍然大悟 :“原来这么简单!”这些问题一般都能够用初等数学知识来解答,但令学生们抓狂. 设{Fn}是斐波那契数列(Fibonacci):1,1,2,3,5,8,13,21,34,55,…,即F1=F2=1,当n>2时,Fn=Fn-1+Fn-2(这个递推关系由Girard在1634年发现).我们观察到上述不等式链中对数的底和真数组成的数列2,3,5,8,13恰好是斐波那契数列的一个子列,于是我们提出如下猜想: 通过计算机数值验证可以得到当n≤103时,不等式均成立.因此这也让我们更加相信这一猜想的正确性. nFnn-2n-1logFn+1Fnn-1n320.50.630930.666667430.6666670.6826060.75550.750.7739760.8680.80.8107140.8333337130.8333330.842480.8571438210.8571430.8633610.8759340.8750.8799770.88888910550.8888890.8927730.91000.9898990.9899320.9910000.9989989990.9989993270.999 引理1(Bernoulli不等式):设x≥-2,n∈N,则(1+x)n≥1+nx. 证明当n=1时,显然成立. 以下考虑n>1的情况. 设f(x)=(1+x)n-(1+nx), 则f′(x)=n[(1+x)n-1-1]. 当x≥0时,f′(x)≥0, 所以f(x)单调递增,f(x)≥f(0)=0. 当-2≤x≤0时,因为(1+x)n-1-1≤ |1+x|n-1-1≤0,所以f′(x)≤0, 所以f(x)单调递减,f(x)≥f(0)=0. 所以当x≥-2时,f(x)≥0,即(1+x)n≥1+nx. 注常见的Bernoulli不等式中要求x≥-1,这个引理说明x≥-1的条件可以放大至x≥-2. 则0 (1)首先证明猜想的左半部分. 我们有 因为1+φ-2n-2>1, 又因为φ-2n-2+φ-2n<φ0+φ0=2, 所以-(φ-2n-2+φ-2n)>-2. 由Bernoulli不等式得 因为n≥4,所以 (2)下面证明猜想的右半部分. 我们有 >φ·[1-(φ-2n+φ-2n-2)]. 又因为-(φ-2n-2+φ-2n)>-2, 由Bernoulli不等式得 >φn[1-n(φ-2n-2+φ-2n)]. 证明当n=3时,φ 设n≤k时命题成立,则当n=k+1时, φk-2+φk-3 因为 φk-1+φk-2=φk-2(1+φ)=φk-2·φ2=φk, φk-2+φk-3=φk-3(1+φ)=φk-3·φ2=φk-1, 所以φk-1 证明(1)当k≥2且n>k时, (2)当k≤1时, 证明(1)当n≥3时, (2)因为



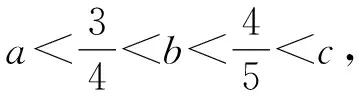



2 猜想的证明











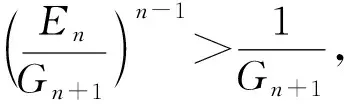

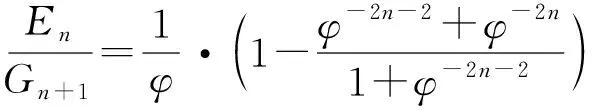



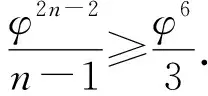

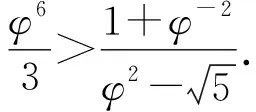



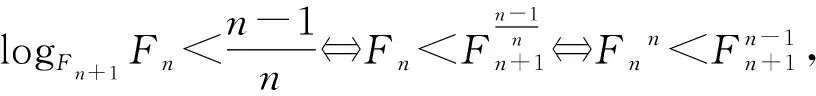
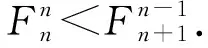




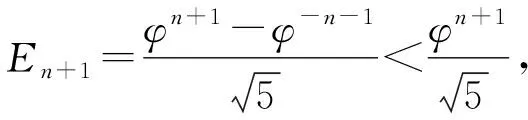
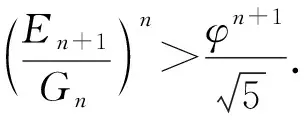
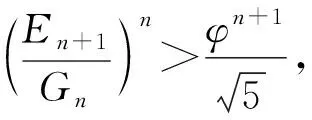

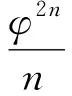






3 推论与探索