高品质课堂：重在优化数学任务的设计 ①——“二倍角三角函数(2)”同课异构的设计、实录与评析

华志远

(无锡市第一中学 214031)

新一轮课程改革，学生关键能力和核心素养的培养倍加关注，但要把新课程理念转化为教师的高水平教学行为，则需要有效的教研抓手，“同课异构”是重要的途径之一. 在一次名师工作室活动中，甲、乙两位教师分别执教“二倍角三角函数(2)”. 从课堂教学的目标、进程和效果来看，两位教师的教学目标合理，所选例题和练习难度与教材相当，但教学的出发点、内容的组织和师生互动的形式有明显的区别. 教师甲的课堂：从复习公式、学生练习开始，到例题讲解、变式训练，最后作归纳总结，课堂条理清晰，训练扎实，但课堂气氛略显沉闷，学生思维的活跃度不够；教师乙的教学从探索规律、解决问题出发，探索数学问题的本源和联系，体现了数学任务驱动的课堂特点，在组织例题教学时，打破教师讲解与学生练习的界限，突出了学生的积极尝试、思考交流和归纳总结，加上他活泼开朗的性格、风趣时尚的语言以及与学生亲密无间的交流，让人感受到高品质课堂的韵味和气息. 限于篇幅，下面提供两位老师的教学设计，并作简要分析，供同行研讨.

1 教师甲的教学设计与实施流程

1.复习倍角公式及其变形，组织学生练习(板演)，教师巡视，并作适当引导.

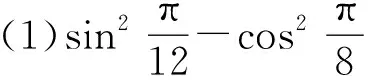
则cos 2α=________.

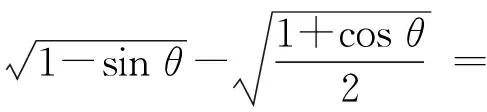
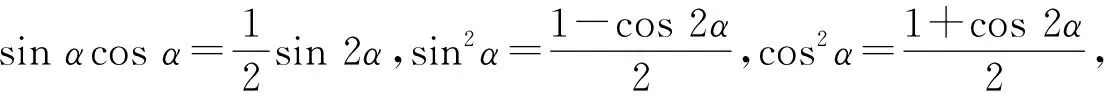
2.呈现例题，分析讲解.

例1化简sin2(α-30°)+ sin2(α+30°)+cos2α.

分析：方法1用正弦的和差角公式直接展开、化简；方法2先降幂、再展开、化简.(解完后作对比分析，并加以归纳总结)

变式练习：求证：cos2(A+B)-sin2(A-B)=cos 2Acos 2B.

例3在半圆形钢板上截取一块矩形材料，怎样截取能使这个矩形的面积最大？

分析：本题既可设边长为自变量，也可设角度为自变量，但旋转类及直角三角形等问题，设角为自变量解题较为简洁.

变式练习：求函数y=sinx(sinx+cosx)的最大值和最小值.

3.总结题型，提炼方法.

求解三角题时：

(1)注意角度变换，如未知角与已知角的关系，相关角与特殊角的关系等；

(2)注重函数名的变换，如化同名函数，正切与正余弦函数共存时化切为弦等；

(3)注意运算结构的变换，如二次根式的升次，和差算式中的降次，合理的通分、约简、消去等.

2 教师乙的教学设计与实录分析

例1计算下列各式：

(1)cos230°+ cos290°+ cos2150°=

.

(2)cos215°+ cos275°+ cos2135°=

.

(3)cos245°+ cos2105°+ cos2165°=

.

根据上述计算结果，写出一般性的结论，并加以证明.

教师追问1：这两个一般性结论本质上是否相同？哪一个等式更优美？为什么？

教师追问2：直接展开证明与降幂后展开，哪种方法更有数学价值？为什么？

教师：前两天，我们班一位同学问了我一道平面几何题，我苦思冥想了半节课，不得其解，请教同事也是一筹莫展，后来突发奇想，能否采用解直角三角形及三角变换来证明呢？结果不到两分钟就证明出来了，那时真的很有成就感.大家也来想一想，怎样证明？

例2如图，在Rt△ABC中，AB⊥BC，∠BAC=30°，E为AC的中点，在CB的延长线上取一点D，使∠BAD=10°，在AD上取一点F，使EF⊥AC.求证：AF=CD.

教师：有些代数题，如,例3已知x2+y2=1，求3x2+2xy+y2的最大值和最小值，看似常规，直接用消元法求解，却因为出现根式而不易把握，怎么办？

学生普遍认为，采用三角代换，可以起到降次、降元，并把问题转化为三角函数的最值，再化归为y=Asin (ωx+φ)的最值求解，最后引导学生总结出三角代换的若干原则.

教师：三角变换不仅能解决平面几何、代数中的困难问题，还能解决一些实际问题.我手里拿的是半径为30 cm的半圆形金箔纸，现要剪出一张矩形纸片，怎样裁剪才能使这个矩形面积最大？为了不进行破坏性试验，我复制了两张同样大小的废报纸，供大家设计、尝试时使用，裁剪方案怎样设计呢？(图与上节例3相同)

变式练习：半径为30 cm的圆形金箔纸，现要剪出一张矩形纸片，怎样裁剪才能使这个矩形面积最大？(呼应半圆与圆形的区别与联系，并从“完形”的角度揭示其联系)

教师：如果要测试本节课的学习效果，能否编制一份三个题目的测试卷？前后四人一组，可以分工协作，五分钟后作评比.

实录分析：从视频展示台上展出的测试题来看，虽然大部分题目只是例题的变形，但从学习者的角度选择这种变式，需要一定的归纳、总结、反思和评价能力，而这正是布鲁姆学习评价中倡导的最高层级.在教师引导下，课堂小结在“为什么要编制这样的测试题”的主题中完成.这里列举其中的若干题目：

(1)求值：cos210°+ cos250°+ cos270°.

(2)求证：cos2α+cos2(α+30°) -

(4)已知x2+y2=4，求x2+2xy-y2的最大值和最小值.

(5)分别求斜边长为2的直角三角形的面积和周长的最大值.

3 执教者的专业背景分析及评价

从两位教师的自我介绍来看，教师甲长期从事毕业班教学，因此对常规题、套路题的训练极为重视，而对培养学生的兴趣、能力、素养等方面关注甚少，因此课堂教学呈现出一定的单一性和封闭性.具体表现在题目的分析切入过早，且过于直接，求解的推进过程较快，归纳小结时学生参与较少，而模仿性、巩固性练习较多，虽然短期效果较好，但从长期来看，学生难以形成高认知水平.

教师乙只完成了高中一轮的循环教学，现在是某一课题组成员.在听课交流中，他对本节课的教学定位，除了知识、技能和方法目标外，对如何使学生亲身经历数学化的过程，体现“做中学”的数学教学理念；如何设计数学任务可以促进学生对数学的理解、提高学习的兴趣；如何创设问题情境，才能发展学生的思维能力，提升学生的数学素养，分别提出了自己的教学主张.如例1的问题提出，他借鉴了选修教材中关于“归纳推理”的要点，提高学生的观察、分析和概括能力；从审美的眼光来判断，等式中角度的对称性更能吸引人们的关注；证明等式两种方法的比较时，学生觉得直接展开更省心，但从数学和物理的角度来分析，降幂后得到的等式“cos (2α-120°)+cos 2α+cos (2α+120°)=0”更具有科学价值.一方面，它以单位圆上内接正三角形“四心合一”为背景，又与以原点O为起点、两两夹角相等的三个单位向量之和为零向量作呼应，沟通了不同数学模型之间的内在联系；另一方面，它与物理中共点力的平衡和三相交流电等领域相关联，体现了不同学科模型之间的融通，从而展示了经典例题的教学价值、美学价值和创新价值，因此在师生作出解题方法价值判断时，教师的示范和引领使教学对话更具有渗透力和感染力，从而体现出高认知水平数学任务的特征.由此可见，成功的教学案例背后，一定有先进的教学理论和科研团队作支撑，同时也体现了教师个人的教学追求和深入的教学思考.

4 同课异构活动的教学评议与反思

4.1 教学评议

在评课活动中，多数教师认为：两节课的教学要求都符合学生的学情，选择的例题主要来源于教材.甲的教学与平时的常态课更接近，只是在练习题、变式训练和课堂小结上，做得更精细和规范，课堂上教师的示范和学生的练习较多，语言和情感交流较少.例如，出示例2后，教师直接利用提示语，找到解题的路径，课堂看似顺畅，教学用时较少，其实对初学者而言，“三大变换”思想还没有真正纳入到学生的认知结构中，因此运用时显得较为迷茫，若能让学生独立尝试探索，哪怕是走些弯路，再与教师、同伴作交流，并作反思和总结，都更加能促进学生理解.乙的教学设计则突出了典型例题故事化、情景化的特点，从而使枯燥乏味的内容变得饶有兴趣.如例1的抢答训练与猜测结论、等式的审美鉴赏和融通价值的讨论，例2平面几何背景的故事化和三角工具作用的渗透，例3的数学实验以及圆与半圆辩证统一的揭示，课堂小结则与编制测试题有机结合，整节课给人的感觉是：立意新颖，手段丰富，衔接自然，灵动活泼，一气呵成.课堂上师生对话流畅，互动自然，学生思考的时间较多，探索的空间较大，反思总结较具体，对发展学生的思维和素养大有裨益.

从两个班学生的认知基础和水平来看，学生对公式和方法的掌握都较为熟练，表现在课堂开始的诊断性练习和课中的变式训练，学生的解题速度和正确率都较高，但学生学习数学的习惯却具有明显的差异.教师甲因为是借班上课，加上原来上课形成的习惯，学生都是以听讲、笔记和模仿练习为主，主动参与思考、讨论和交流的意识较为薄弱，多数同学在解题获得结果后就出现了懈怠情绪；而教师乙所教的学生，由于受其教学的长期熏陶，因而面对数学问题，思考积极，敢于探索，发言踊跃，在解题完成后善于归纳、总结和反思，这在编制测试题中表现尤为突出.俗话说名师出高徒，学生的高认知水平来自于教师的不断影响.高品质课堂重在优化数学任务的设计，而高水平的任务设计又必须依赖于高素质的教师队伍，从而引领学生不断提高认知水平.

4.2 教学反思

处理好应答练习与尝试体验的关系.从学习过程来看，数学学习依托于学生对知识的理解和建构，依托于对数学问题本质的把握，依托于积极的深度思考，因此，经验和体验在数学学习中起着及其重要的作用.在学习中如何唤醒学生的经验，最科学的教学方法就是创设问题情境，激发学生的好奇心，让他们主动参与探索，从而经历问题的发生和发展过程.应答练习固然能起到巩固知识的作用，但不利于学生明辨知识产生的因果链，学习者难以真正体验蛰伏于知识深层处的数学思想方法．

处理好局部与整体的关系.传统的课时教学将学习内容单一化、碎片化，学生往往难以体验数学知识之间、不同单元之间以及与社会现实、其他学科之间的联系，大单元教学法则以发展学生的能力和素养为目标，从整体上综合协调数学知识、方法、思想、能力及素养等各要素之间的关系，即将单元学习的各步骤和各环节，都放置到教学活动的大系统中加以统筹，而不是片面凸显或强调某一知识点.这样在单元整体性设计的学习框架下，新旧知识的关联性、数学各分支的内在联系以及数学思想方法之间的连贯性，通过一个单元的学习，不断得到巩固、完善和发展，从而彰显了其系统化和过程性的特征，从而使学生的数学学习在整体中感受局部的作用，在局部中领悟整体的意义，以保证整个单元的学习环环相扣，有序推进.这就要求教师必须有宏观把握教材的能力，并依据学生的学情，从探索规律、解决问题出发，探索数学问题的本质和联系，体现数学任务驱动的课堂特点，在组织例题教学时，打破教与学的界限，突出学生的积极尝试、思考交流和归纳总结，从而使学生成为知识的发现者、建构者、对话者和反思者，以构建起良好的认知结构，提升学生的能力和素养.