旋流器内两种非牛顿流体的流动行为分析
2021-10-08邓鑫谢超马强张进
邓鑫,谢超,马强,张进
(中国石油天然气管道工程有限公司,河北 廊坊 065000)
水力旋流器是钻井液固控系统的重要组成部分,根据离心沉降原理实现两相或多相分离[1-3]。含固相颗粒的料液在一定压力或速度下切向引入旋流器,产生强烈的旋转运动,在离心力作用下,颗粒相产生沿固体壁面的外旋流运动,但是由于径向流体曳力的阻碍,不同性质的颗粒沿旋流器径向方向重新分布,密度小或粒度细的颗粒随流体迁移至内旋流器经溢流口排出;而密度大、粒度粗的颗粒借助较大的离心力由底流口收集,达到分离或分级目的[4-5]。
CHU[6]采用CFD-DEM(离散元分析方法)分析了旋流器内颗粒在水中的运动轨迹以及受力。MOGNON[7]以水为流体介质,通过添加黏性添加剂来代替钻井液,分析了随黏度变化旋流器中细微颗粒的分离过程。MARTHINUSSEN[8]实验研究了水力旋流器中高黏度液体颗粒的分离性能,用于指导水力旋流器几何形状的改进,使其更适合黏性流体。艾志久[9]用幂律流体与水描述钻井液,通过CFD 数值模拟方法分析了两种流体在旋流器内旋流特性的差异。结果显示幂律流的静压、轴向速度及径向速度均大于水,并且零轴速包络面(The locus of the zero axial velocity vectors,简称LZVV)更靠近壁面,但切向速度显示幂律流体要小于水。
钻井液是属于宾汉模式与幂律模式间的一种非牛顿流体,在模拟水力旋流器两相分离时,使用传统流变参数模式描述钻井液,在全剪切速率下并不能保证准确性[10]。樊洪海[11-12]提出一种新型四参数钻井液模式,能满足各种剪切速率下对钻井液流变行为的描述。刘洪斌[13]分别使用四参数流体、幂律流体、水作为流体介质,通过CFD数值模拟方法对比分析了流体的旋流特性,得出非牛顿流体的静压力与轴向速度要大于牛顿流体,切向速度要小于牛顿流体;四参数流体静压与切向速度均小于幂律流体。
本文采用同种钻井液的两种表达方式——四参数模式和幂律模式,结合雷诺应力模型(Reynolds Stress Model, 简称RSM),对比分析两种非牛顿流体钻井液在水力旋流器内的旋流动行为以及差异的分布情况。
1 数值模拟方法
1.1 物理模型以及网格划分
在HSIEH[14]模型基础上改进模型,按比例尺为1∶1 建立双进料口模型[15],入口截面形状为矩形,如图1 所示。两个进料口保持进料速度相同。建模坐标原点位于旋流器顶盖圆心处,水力旋流器截面尺寸视图如图2 所示,尺寸信息如表1 所示。使用ICEM 划分结构网格,共计23.5 万网格单元,如图3 所示。通过多次计算,发现进一步增加网格单元数时,并不能提高计算结果的准确性。根据HSIEH实验条件,采用相同边界条件验证物理模型以及计算模型。HSIEH 质量流量为66.99 kg·min-1,换算为速度入口,可得本模型入口速度为2.23 m·s-1。与HSIEH 切向速度实验数据对比,发现除了在极大值位置偏低外,其他各个位置速度吻合良好,如图4所示,与唐波[16]验证所得结果类似。
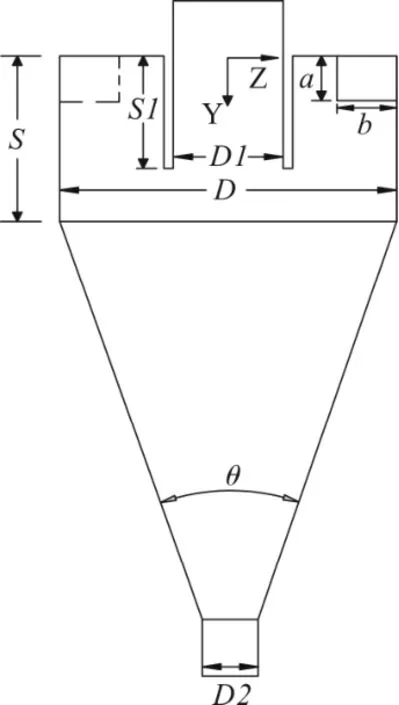
图1 水力旋流器ZY 截面

表1 水力旋流器截面尺寸
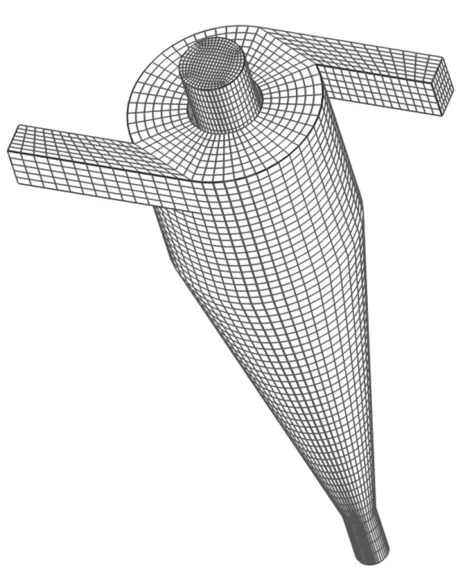
图2 模型网格
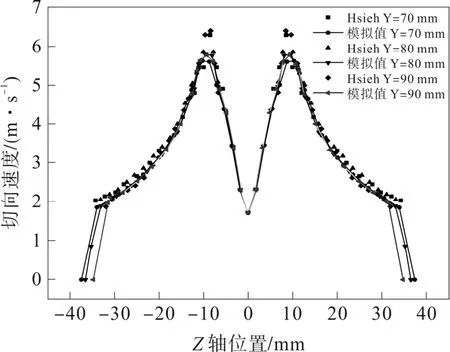
图3 切向速度计算值与测量值对比
1.2 四参数模式钻井液

式中:τ—切应力,Pa;
τo—屈服应力,Pa;
a—黏度系数,Pa·s;
γ—剪切速率,s-1;
b—稠度系数,Pa·sn;
n—流性指数,无因次。
选用1 组水泥浆的黏度计读数,通过回归算法,分别得到幂律模式与四参数模式的流变参数[17],如表2 所示。模拟钻井液在水力旋流器内旋流作业时,分别采用四参数模式和幂律模式作为流体介质,其中四参数模式钻井液流变参数采用用户自定义功能编译。
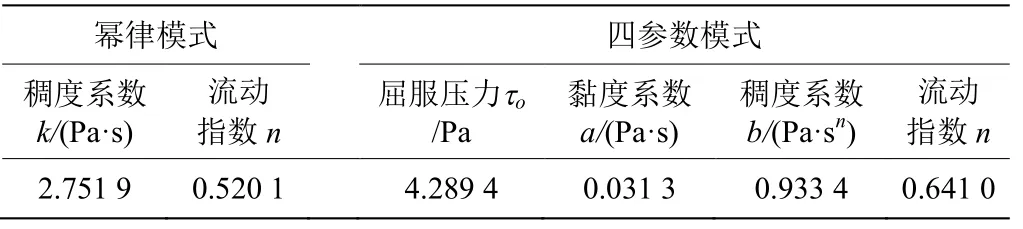
表2 流变参数计算结果
1.3 计算模型及边界条件
RSM 模型在对雷诺应力的计算过程中,尽可能全面地考虑了可能引起雷诺应力变化的各种因素。其中的压力场和流体旋转引起的应力产生项和系统旋转产生项尤为重要,水力旋流器工作过程中,流体进入旋流器后,在很小的空间内做高速旋转运动,其压力梯度、切向速度梯度都很大,所以压力梯度和流体旋转对雷诺应力的影响不能忽略。相比于k-ε模型、RNGk-ε模型更适合模拟水力旋流器内的流场运动。
设置入口速度为10 m·s-1,从入口方向垂直进料。根据旋流器实际工作情况,出口边界条件均设大气压,空气回流指数设为1。壁面边界条件为无滑移壁面,近壁面为壁面函数法。压力速度耦合采用SIMPLEC 算法,压力离散采用PRESTO 方法,其余变量采用二阶迎风格式,各项收敛残差精度设为10-5,当溢流口与底流口流量变化小于5%时,视为计算达到收敛状态。
连续相控制方程:

动量守恒方程:

雷诺应力输运方程:
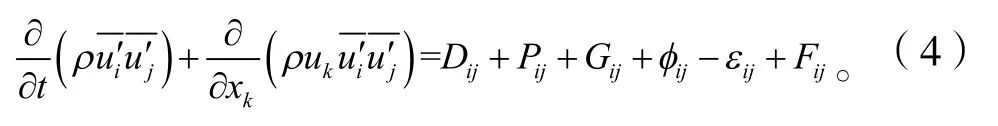
式中:Dij—湍流扩散项;
Pij—应力产生项;
Gij—浮力产生项;
ij—应力应变再分配项;
ɛij—离散相;
Fij—系统旋转产生项。
2 计算结果与探讨
分别采用幂律模式与四参数模式描述钻井液参与计算。观察旋流场ZY平面上计算云图,并绘制ZY平面上Y=45 mm、Y=75 mm、Y=115 mm、Y=150 mm、Y=200 mm 上的数据图,对比分析两种模式钻井液的切向速度场、压力场及湍流强度差异。
2.1 速度场分析
2.1.1 切向速度对比
全计算域下,幂律模式最大值为20.96 m·s-1,四参数模式为20.47 m·s-1。在ZY平面上,幂律模式最大切向速度为20.49 m·s-1,四参数模式最大为19.95 m·s-1,最大值均出现在中心空气柱两旁,如图4 所示。四参数模式切向速度小于幂律模式,这对二者的固相分离效率影响较大[18]。
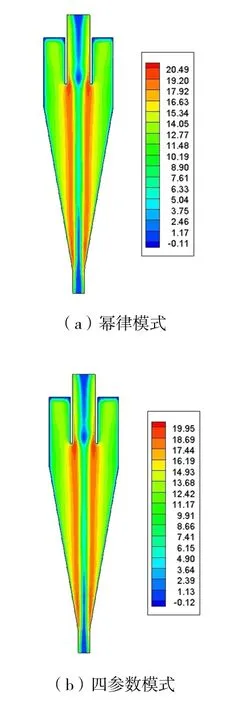
图4 ZY 平面切向速度图
两种模式计算下剪切速度分布相似,均表现为在轴心附近变化剧烈,从Y=45 mm 到Y=200 mm,轴心切向速度变化先由小到大,再由大到小;两种模式下各个横截面切向速度极值出现位置相同,极小值出现在Z=0 mm处,极大值出现在Z=±9 mm处。四参数模式各位置切向速度计算结果均低于幂律模式,如图5 所示。
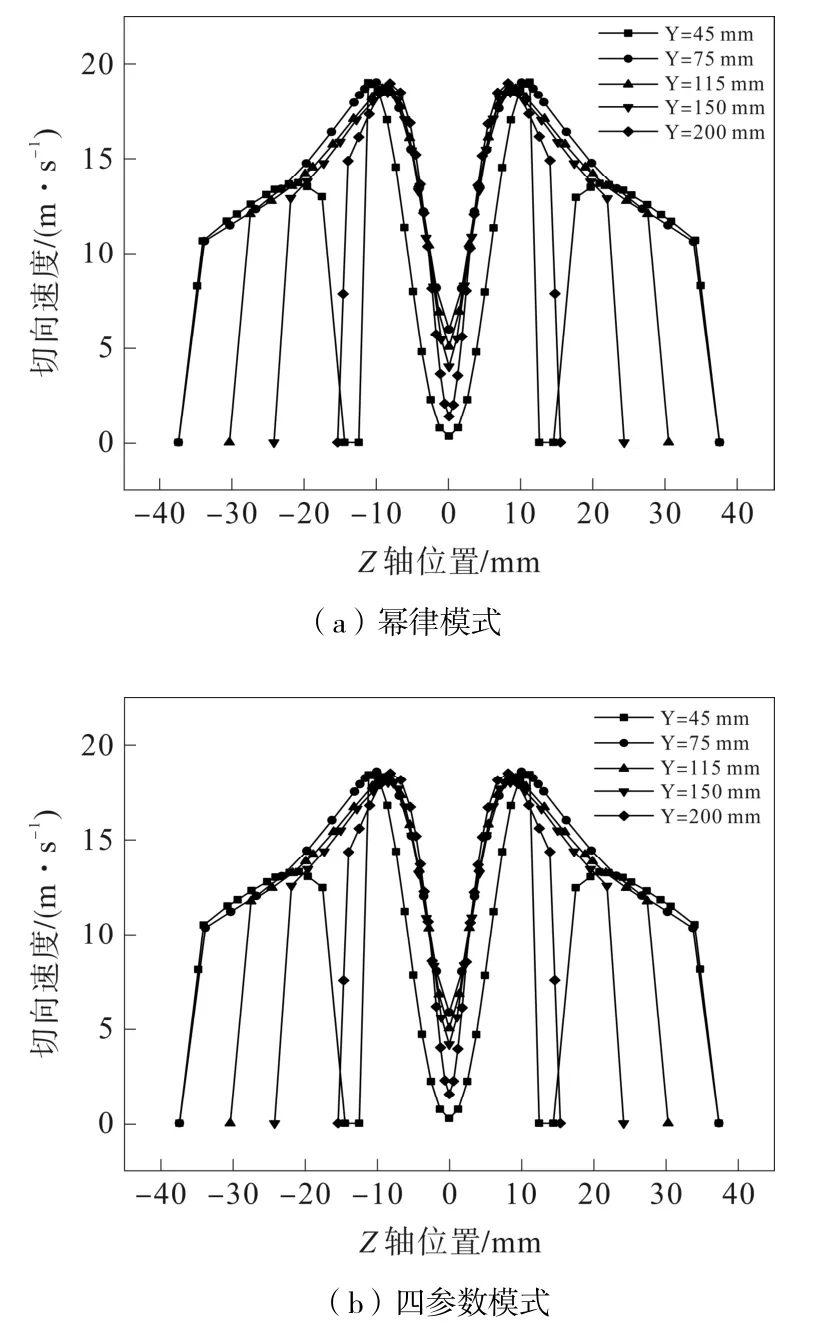
图5 Z 轴方向切向速度曲线图
2.1.2 轴向速度对比
在全计算域中,幂律模式最大轴向速度为 48.38 m·s-1,最小轴向速度为-37.49 m·s-1;四参数模式最大轴向速度为48.85 m·s-1,最小为-35.53 m·s-1,四参数模式的上行流速度明显低于幂律模式。图6为幂律模式与四参数模式的ZY截面轴向速度云图,二者轴向速度最大值出现在靠近底流口位置,最小值出现在溢流口附近,与实际工作情况相符。图7为两种模式计算条件下,旋流器内的LZVV 轮廓图,幂律模式与四参数模式LZVV 形状相似。在溢流管壁面与旋流器外壁面之间,由LZVV 所包围的气包状区域为循环流区域,四参数模式计算下的循环流区域比幂律模式更大。循环流区域越大,颗粒在此区域停留时间越长[19]。
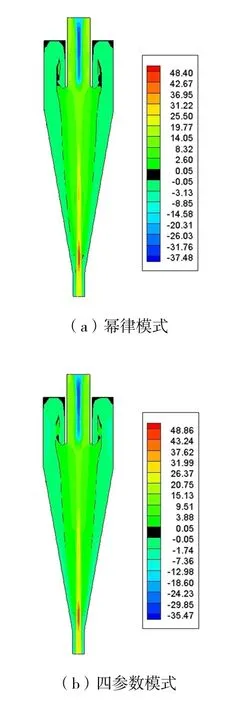
图6 ZY 平面轴向速度云图

图7 LZVV 轮廓图
图8 为Z轴方向轴向速度曲线图。由于空气回流的影响,靠近底流口与溢流口处的轴向速度波动明显,且两种模式计算值在此位置差异较大。旋流器中间段轴向速度波动较小,两种模式轴向速度在此差异小。
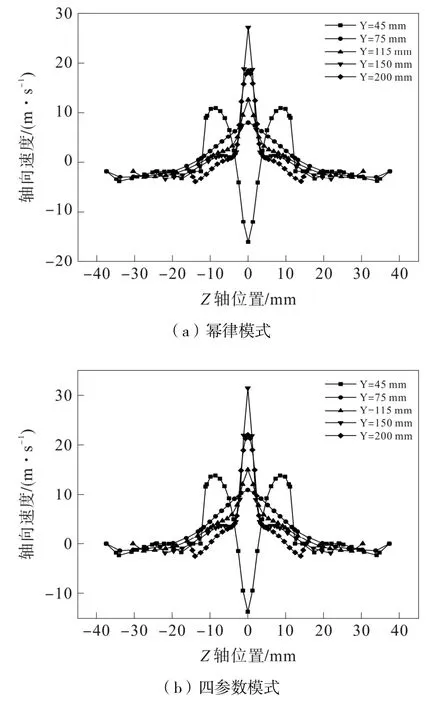
图8 Z 轴方向轴向速度曲线图
2.1.3 径向速度对比
在全计算域中,幂律模式最大径向速度为3.45 m·s-1,四参数模式最大径向速度为3.19 m·s-1。图9 为两种模式计算下的ZY平面径向速度云图,二者径向速度最大值均出现在溢流管入口处[20],整体速度分布类似,四参数模式在各个位置径向速度略低于幂律模式。
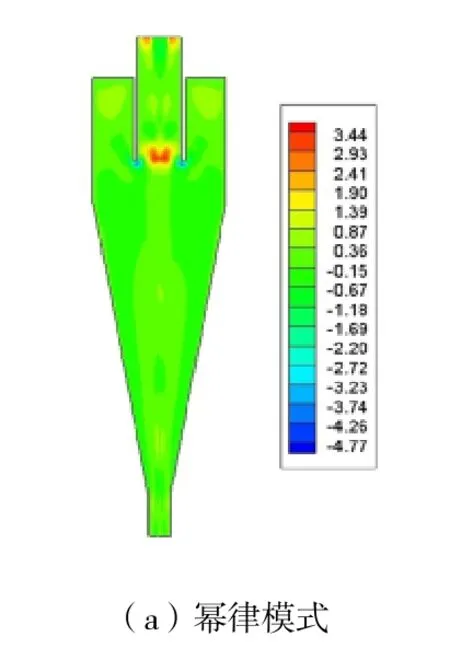
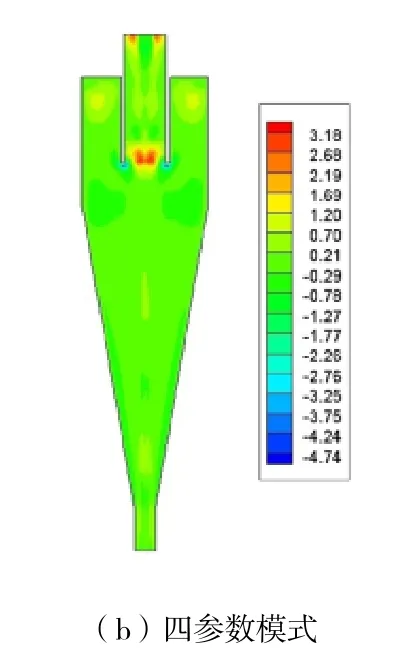
图9 ZY 平面径向速度云图
四参数模式与幂律模式径向速度差异主要出现在溢流管内,其他各个位置的径向速度相差较小,如图10 所示。

图10 Z 轴方向径向速度曲线图
2.2 压力分析
2.2.1 静态压力对比
在旋流器分离过程中,压力降是表征旋流器分离性能和能量损耗的主要参数,对分离粒度和分离效率也有重要影响[21]。全计算域中,幂律模式最大静压为0.868 MPa,入口与底流口的平均压降为0.867 MPa。四参数模式下的最大静压为0.837 MPa,入口与底流口的平均压降为0.836 MPa。固相颗粒所受压力梯度力指向轴心方向,四参数模式内压力梯度力小于幂律模式。四参数模式入口与底流口平均压降小于幂律模式,说明四参数模式压力损耗较幂律模式更小。图11 为两种模式下ZX平面静压云图,可以看出最大静压均出现在壁面位置,最小静压均出现在旋流器中心处。
旋流器Z 轴方向的静态压力分布如图12 所示。
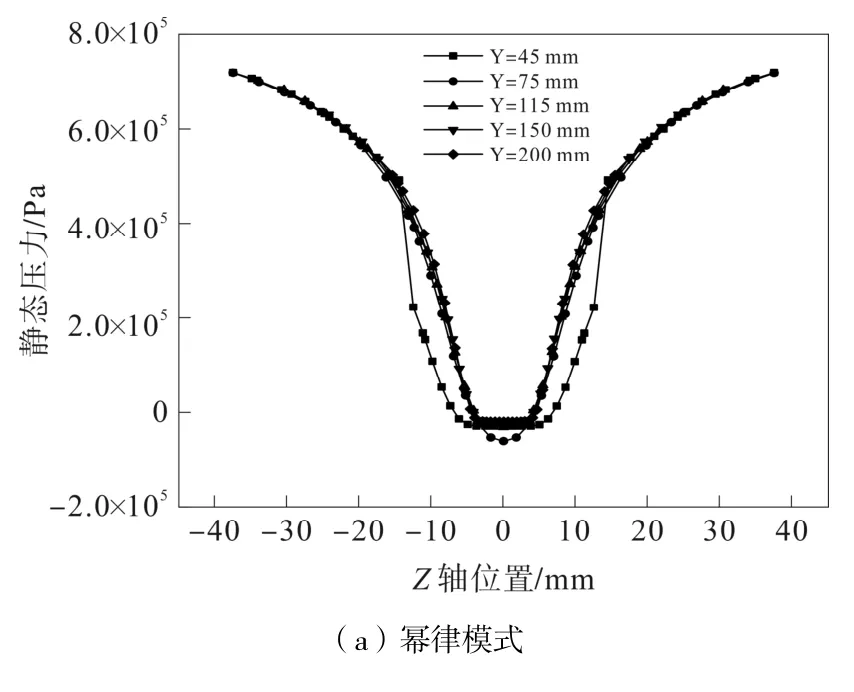
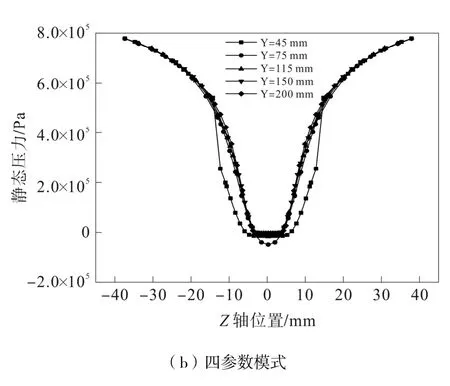
图12 Z 轴方向静态压力曲线图
两种模式在轴心附近的压力分布差异很小,随着Z的增大,两种模式的压力值逐渐增大,在轴心位置出现零静压是由于存在空气柱的原因,符合组合涡流场的压力分布规律。四参数模压力增长速率比幂律模式小,在壁面区域时,二者压力差值达到最大。这说明四参数模式与幂律模式由于本构方程以及流变参数的不同,在旋流器内运动时,对壁面区域压力的影响最大。
2.2.2 动态压力对比
在全计算域中,幂律模式计算下最大动态压力为0.466 MPa,四参数模式计算下最大动态压力为0.444 MPa。图13 为ZY平面动态压力分布云图,最大值均出现在溢流管壁面,最小值出现在轴心。四参数模式计算值在各个位置均低于幂律模式,溢流管壁面表现最明显,如图14 所示。
2.3 湍流强度对比
观察湍流强度发现,两种模式计算结果均显示在溢流口与底流口附近湍流强度最激烈。幂律模式计算下最大湍流强度为7.99,四参数模式最大为7.90,图15 为ZY平面湍流强度云图。
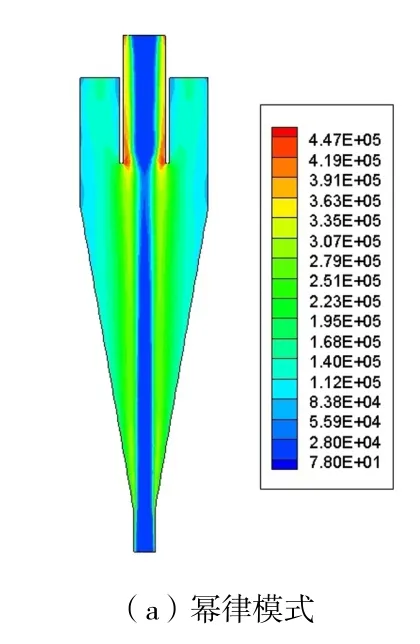
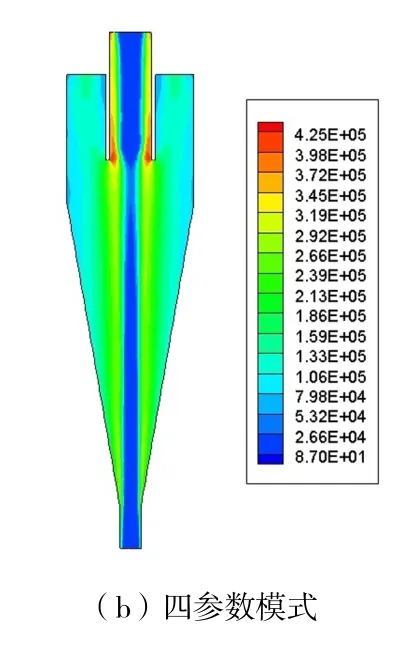
图13 ZY 平面动态压力云图
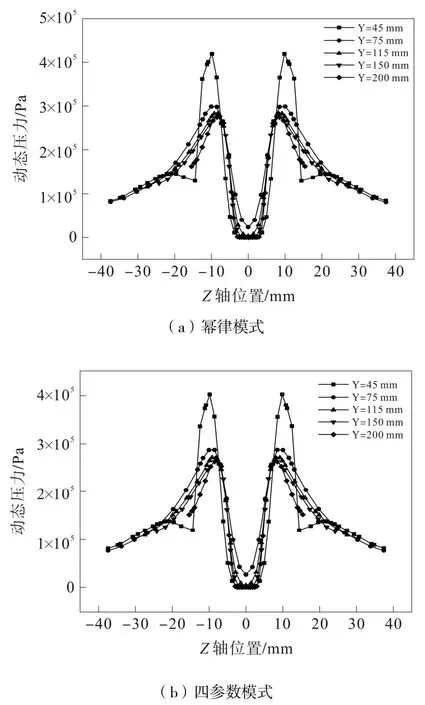
图14 Z 轴方向动态压力曲线图
四参数模式计算下各个位置湍流强度均低于幂律模式,其中在溢流管内表现最明显,如图16 所示。
3 结 论
通过四参数模式与幂律模式钻井液在水力旋流器内速度场、压力场及湍流强度的对比分析,得出以下结论:
1)四参数模式计算下的切向速度低于幂律模式,这使得在四参数模式中,对固相颗粒的分离效率更低。四参数模式轴向速度整体大小低于幂律模式,上行流速度明显低于幂律模式;LZVV 形状相似,四参数模式计算下的循环流区域比幂律模式大,固相颗粒在此模式中停留时间更长。径向速度差异主要出现在溢流管内。
2)四参数模式钻井液的静态压力低于幂律模式,旋流器入口与底流口的平均压降低于幂律模式,说明四参数压力损耗更低;四参数模式中,颗粒所受压力梯度力将小于幂律模式。四参数模式计算下的动态压力略低于幂律模式,在溢流管壁面表现最明显。
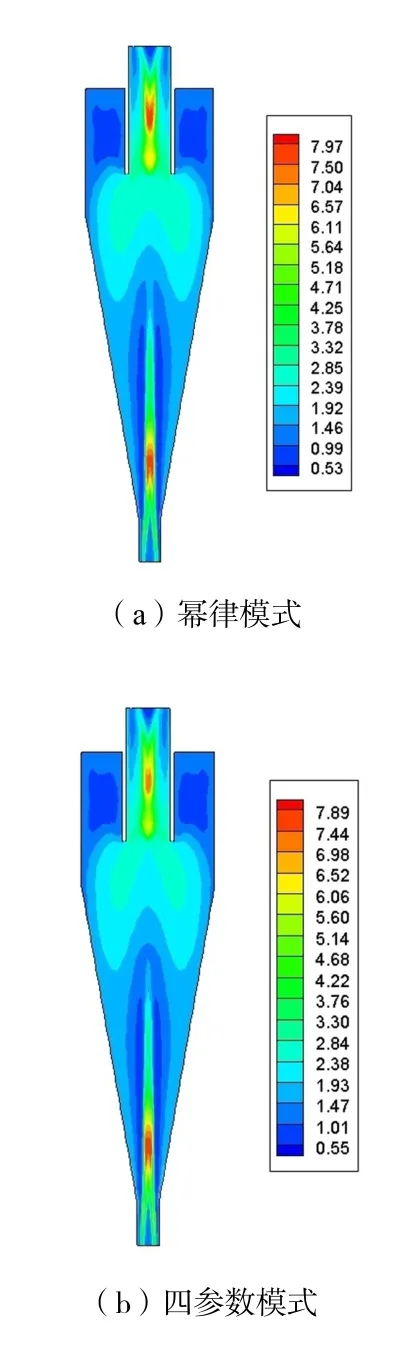
图15 ZY 平面湍流强度云图

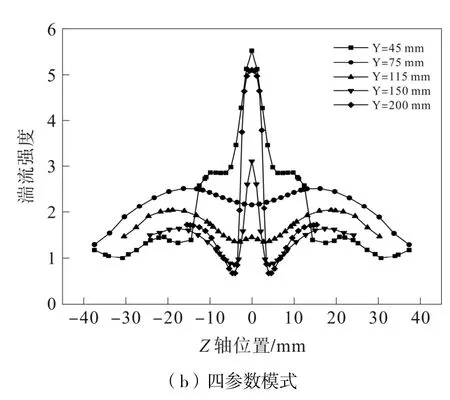
图16 Z 轴方向湍流强度曲线图
3)通过对湍流强度的分析,四参数模式计算下湍流强度略低于幂律模式,在溢流管内差异最大。
4)通过四参数模式分析钻井液的流动行为结果可靠性高于幂律模式。
