基于混合粒子群优化算法的火箭弹内弹道优化设计

曹 林,孟吉红,范 匆,张 翱,杨赵兵,邓 聃

(四川航天系统工程研究所,四川 成都 610100)

无控火箭弹是一种以固体火箭发动机为主要动力装置的弹药,火箭弹武器系统具备火力压制和面打击能力。由于具有较高的效费比,无控火箭弹在现代常规战争中仍然发挥着不可替代的作用。

固体火箭发动机设计是无控火箭弹总体设计的重要组成部分,发动机的性能直接决定了火箭弹能否满足总体设计指标的要求。近年来,国内外学者针对固体火箭发动机的优化设计问题开展了大量的研究工作,并取得了众多有价值的成果。何景轩等[1]通过建立固体火箭发动机优化模型,采用遗传算法,以发动机冲质比为目标函数,得到了优化的发动机工作压强、喷管扩张比和喉径等参数。王鹏等[2]采用遗传算法,获得最优体积比重下的发动机各项参数。在固体火箭优化设计领域,有较多学者采用物理规划方法、设计空间确定法、单学科可行方法等进行火箭发动机结构、装药、尾喷管等方面的研究[3-7]。从飞行器总体设计的角度,范健等[8]采用火箭发动机内外弹道联合仿真的方法,对火箭发动机内弹道参数进行了优化设计,获得了优化的推力曲线,该方法有助于减少总体和动力系统之间的迭代次数,对整个飞行器的动力优化具有指导意义。李晓斌等[9]从总体设计的角度,考虑各项约束,采用不同的优化方法对助推器进行了优化设计。

综上所述,针对固体火箭发动机优化设计的大部分研究工作均是从动力分系统的角度进行发动机结构或内弹道参数的优化设计,鲜有学者从飞行器总体的角度出发进行内外弹道联合优化。因此,本文从总体设计的角度出发,重点关注固体火箭发动机内弹道特性与火箭弹有效射程之间的联系,对固体火箭发动机的内弹道曲线进行优化,研究结果对无控火箭弹的总体设计具有一定的理论和工程指导意义。

1 优化问题描述

从数学理论的角度来看,本文所研究的发动机内弹道优化设计可简化为带有约束条件的一般优化问题,其数学模型为

(1)

式中:X=(x1x2…xn)T∈Rn为优化变量,Ω为优化变量X的可行域。f(X)为目标函数,g(X)为等式约束条件,h(X)≠0为不等式约束条件。其中,目标函数f(X)和优化变量X之间存在一一对应的隐式关系,不便于采用传统优化方法进行求解,需进行有针对性的优化策略设计。

2 固体火箭发动机内弹道优化设计

以某型122 mm无控旋转式火箭弹为背景,进行固体火箭发动机的内弹道优化设计。根据求解一般优化问题的方法,构建固体火箭发动机内弹道优化策略,其结构框图见图1。如图1所示,该优化策略主要由4个模块组成,即内弹道参数化建模、总体设计指标描述、适应度函数构造和优化算法设计。

图1 固体火箭发动机内弹道优化策略框图

2.1 内弹道参数化建模

参照固体火箭发动机的典型推力曲线类型,对工程上应用较为广泛的单推模式和双推模式的推力曲线进行参数化建模。

①单推模式。

单推模式的推力曲线示意图如图2所示。单推模式的发动机推力特性可表示为

图2 单推模式推力曲线示意图

(2)

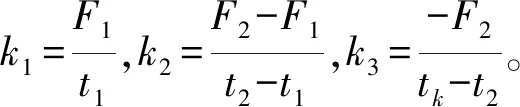
(3)

②双推模式。

双推模式的推力曲线示意图见图3。如图3所示,双推模式的发动机推力特性可表示为

图3 双推模式推力曲线示意图

(4)

(5)

综上可知,发动机的推力特性可由设计参数X=(t1t2tkF1F2)T进行完全描述。

2.2 总体设计指标

总体设计指标表征了无控火箭弹的总体性能。除火箭弹的结构参数外,工程上重点关注的总体设计指标主要有射程、密集度、毁伤半径等,其中射程与固体火箭发动机的内弹道特性密切相关。鉴于本文所研究的问题,假定影响射程的其他因素(如弹形系数、空气动力系数等)均为定值,则射程L与发动机参数化模型的设计参数X之间存在一一对应的关系:

L=f(X)

(6)

一般来说,发动机的总冲越大,火箭弹的射程越远。然而,增大发动机的总冲将消耗更多的推进剂质量,降低火箭弹的效费比。因此,假定在发动机总冲恒定的约束条件下,对火箭发动机的内弹道进行优化。

2.3 适应度函数

对于求解由式(1)所描述的一般优化问题,目前并无通用的适应度函数构造方法。针对本文所研究的固体火箭发动机内弹道优化设计,采用罚函数方法构造适应度函数ff(X)为

(7)

(8)

(9)

式中:Lref为参考射程。

2.4 混合粒子群优化算法

由于目标函数f(X)和优化变量X之间是隐式关系,无法采用传统优化方法进行求解。因此,针对本文所研究的固体火箭发动机内弹道优化问题,设计了一种新型的混合粒子群优化算法。

2.4.1 算法概述

遗传算法(genetic algorithm,GA)是一类借鉴自然界进化规律演化而来的随机搜索算法,采用简单的编码技术表示各种复杂的数据结构,并通过对一组编码进行简单的遗传操作来实现寻优。与一般随机算法不同,遗传算法将定向搜索和随机搜索有机地结合起来,具有潜在并行性[10]。由于算法不涉及种群的反馈信息,故算法的搜索速度较慢,要得到精确解需要较长时间的训练。另外,如果初始种群、交叉概率、变异概率等选择不当,遗传算法极易过早收敛于局部最优。

粒子群优化(particle swarm optimization,PSO)算法是由KENNEDY和EBERHART于1995年提出的一种仿生类算法,通过个体间的协作与竞争实现多维空间中最优解的搜索,其基本思想是模拟鸟类的捕食过程,粒子在解空间中移动,记录下各自曾经搜索到的最优点和整个种群搜索到的全局最优点,根据自身最优点和全局最优点来更新自己的速度和位置,并通过不断地对极值点的更新来实现快速寻优的目的[11]。经过改进后的粒子群优化算法具有较好的全局搜索能力,但是当算法迭代至接近全局最优解时,整个粒子群搜索全局最优解的速度将变得缓慢。

利用遗传算法在局部区域内快速收敛的特点,当粒子群算法迭代至接近全局最优时,利用遗传算法弥补粒子群优化算法在局部区域内搜索缓慢的缺点,从而尽可能快速准确地找到最接近全局最优的解,其算法示意图如图4所示。在解空间Ω内,从初始位置X0处出发,首先利用改进的粒子群算法进行全局最优解的初步搜索,当粒子群优化算法迭代至指定代数并接近全局最优解时,此时整个种群进入最优解邻域U内,然后利用改进的遗传算法实现局部快速收敛,最终达到全局最优Xopt。

图4 混合粒子群优化算法结构示意图

该算法同时依赖于PSO的全局搜索能力和GA的局部收敛速度。因此,为了加强算法的全局搜索能力,对PSO进行相应改进,如初始种群均匀化处理、惯性权值按照Sigmoid函数自适应调整[12]、学习因子异步变化[13]和引入适应权值的时间飞行因子等。同时,为了加快GA的全局收敛速度,避免对基因编码进行变异操作,使得迭代过程局限在封闭的局部区域内,以实现较快的局部收敛速度。

2.4.2 算法流程

基于GA的混合粒子群优化算法流程图如图5所示。

图5 混合粒子群优化算法流程图

具体算法流程如下:

①优化问题描述,即利用数学方法把实际问题描述成一般优化问题的标准形式;

②利用PSO算法对优化问题进行初步全局寻优;

③当PSO算法迭代至指定代数并接近全局最优解邻域时,结合此时获得的全局次优解和全局最优解邻域,生成新种群;

④从新种群出发,在全局最优解邻域内,利用GA进行快速局部寻优,最终获得最接近全局最优的次优解。

2.4.3 算法测试与分析

本节以3个典型的非线性基准函数作为测试函数对混合粒子群优化算法进行性能测试。测试函数如下。

①Alphine函数。

(10)

②Rastrigrin函数。

(11)

③Schaffer函数。

(12)

应用传统的GA和PSO算法及本文所提出的混合粒子群优化算法对上述3种测试函数进行寻优计算,每种算法均重复测试2 000次,其算法参数设置和测试结果见表1。

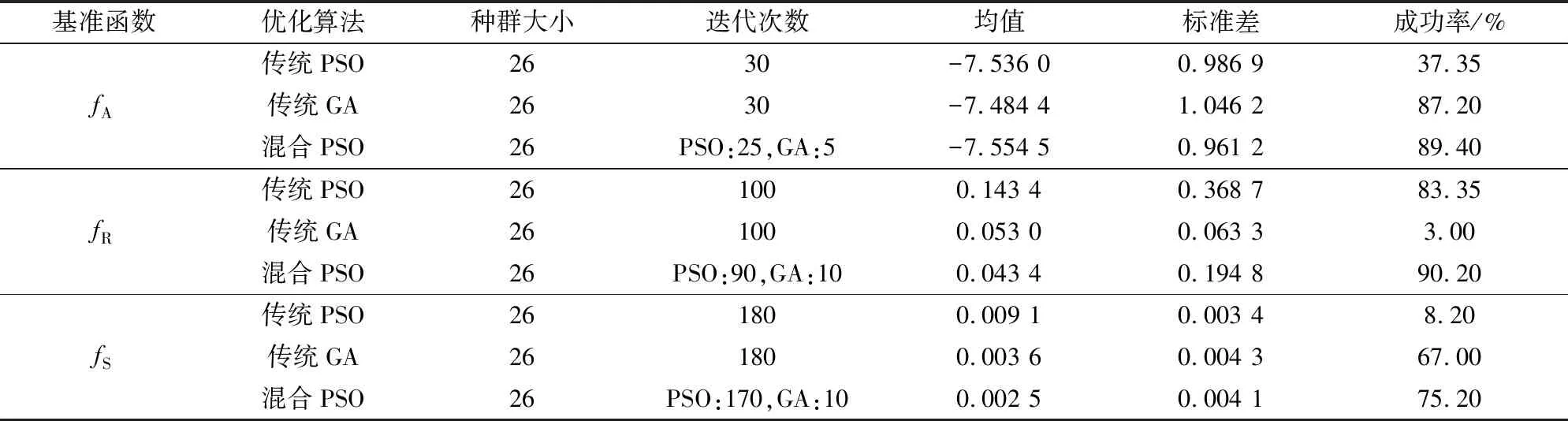
表1 参数设置与测试结果

如表1所示,与传统的GA和PSO优化算法相比,经过改进的混合粒子群优化算法寻优结果具有更接近准确值的均值和较小的统计方差。同时,混合粒子群优化算法找到全局最优解的概率(表示为成功率)分别为89.40%,90.20%和75.20%,在3种函数的寻优测试中均为最高。因此,测试结果表明本文所提出的混合粒子群具有较好的搜索能力和鲁棒性。

2.5 仿真结果分析

平均推力Fave为发动机总冲Isz与参考工作时间tk,ref的比值,即Fave=Isz/tk,ref;

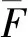
增程率ρΔL为射程增量ΔL与参考射程Lref的比值,即ρΔL=ΔL/Lref=(L-Lref)/Lref。

以典型122 mm无控旋转式火箭弹为算例,针对固体火箭发动机的内弹道优化问题,采用本文设计的混合粒子群优化算法进行迭代寻优计算。优化变量X的可行域X=(x1x2…xn)T∈Rn设置如下。

Xmin=(0 0 0.47 0.523 9 0.523 9)T

Xmax=
(1.566 8 1.566 8 1.566 8 1.467 0 1.467 0)T

采用混合粒子群优化算法对优化问题进行求解,算法迭代15次,得到固体火箭发动机单推模式和双推模式的最优推力特性,如图6所示。优化后的内弹道设计参数如表2所示,表中,N为迭代次数。由表2可知,单推模式和双推模式分别将火箭弹的射程提高了3.75%和4.45%。图7为火箭弹的增程率变化曲线。从图中可看出,双推模式的火箭发动机优化后的增程率略高于单推模式。总的来说,发动机推力随工作时间减小的内弹道特性有利于提高火箭弹的射程。

图6 推力曲线

表2 优化结果

图7 增程率

3 结束语

本文从总体设计的角度出发,对无控火箭弹的内弹道特性进行优化设计。首先,建立了固体火箭发动机单推模式和双推模式的内弹道参数化模型。其次,设计了一种实用的混合粒子群优化算法。通过对典型测试函数的寻优分析可知,该混合粒子群算法具有较强的搜索能力和较快的收敛速度。最后,将该算法应用于典型122 mm无控旋转式火箭弹的固体火箭发动机优化设计,并编写了系统仿真及优化程序。通过仿真结果与分析,得到如下结论:所设计的混合离子群优化算法可以作为解决发动机内弹道优化问题的有效工具;发动机单推模式和双推模式优化后的推力特性,分别将火箭弹的射程提高了3.75%和4.45%。其中,双推模式的增程率略高于单推模式,且发动机推力随工作时间减小的内弹道特性更有利于火箭弹射程的提高。