考虑攻击角约束和输入饱和的制导控制一体化设计
2021-10-08张宽桥刘连照王小臻
张宽桥,刘连照,马 晖,徐 宙,王小臻
(电子信息系统复杂电磁环境效应国家重点实验室,河南 洛阳 471003)
传统的导弹制导控制系统是将制导回路和控制回路分开设计,未考虑两回路间的耦合关系。若目标的速度较快且机动性较强,该设计方法容易导致系统不稳定和较大的脱靶量[1]。制导控制一体化设计[2]是将制导系统和控制系统一起设计,考虑二者间的耦合关系,并充分利用视线角、姿态、过载等综合信息,能有效提高导弹制导控制性能。
针对制导控制一体化设计问题,国内外学者进行了深入研究,采用不同的理论完成了制导控制一体化设计,如小增益理论[3]、θ-D方法[4]、滑模控制[5]、自适应控制[6]等。由于制导控制一体化模型具有严格反馈形式,反演设计方法被广泛用于制导控制一体化设计中[7-8]。反演设计方法需要对虚拟控制量多次求导,存在“指数膨胀”的问题。动态面控制通过引入一阶滤波器来解决对虚拟控制量多次求导的问题,被用于制导控制一体化设计中[9-10]。
为增加战斗部的毁伤效能,诸如反坦克导弹、反舰导弹、防空导弹等,需要以一定的攻击角度命中目标[11]。因此,在制导控制一体化设计中也需要考虑攻击角度约束的问题。文献[12]基于滑模控制和动态逆控制,完成了带攻击角度约束的三维制导控制一体化设计,采用连续近似函数替代符号函数抑制滑模控制的抖振问题。传统的基于动态面控制的制导控制一体化设计,只能保证系统状态渐进收敛至期望值,且引入一阶滤波器导致其快速性降低。
若存在目标大机动、系统内部扰动及外界干扰等因素,控制量幅值会增大,可能会达到执行机构物理约束上限,从而导致控制量饱和。饱和问题的出现可能会导致控制性能下降甚至出现一些不可预测的结果[13]。因此,在制导控制一体化设计中,有必要考虑输入饱和的问题。文献[14]采用改进的饱和函数和一个辅助系统来处理饱和问题,将辅助系统状态用于一体化控制律的设计和稳定性分析。
制导控制一体化设计相关研究很多,但同时考虑攻击角度约束、输入饱和问题的制导控制一体化设计的研究较少,同时由于目标机动、气动系数的摄动以及通道之间耦合的影响,制导控制系统存在建模不确定性,在进行一体化设计时需要加以考虑。本文针对攻击角度约束、输入饱和和模型不确定性等问题,提出了一种有限时间收敛制导控制一体化设计方法。通过导弹六自由度仿真验证了算法的有效性。
1 问题描述
1.1 制导控制一体化设计模型
构建制导控制一体化设计模型前,做如下假设:
①导弹在末制导段无动力飞行,且速度vm变化不大。
②导弹的速度倾斜角γv在末制导段为小角度,且sinγv≈0,cosγv≈1。
建立如图1所示的三维惯性坐标系下导弹与目标的相对运动模型。图中,Oxyz为惯性坐标系,Ox4y4z4为弹目视线坐标系,M和T分别表示导弹和目标的位置,ε和η分别为弹目视线倾角和偏角,R为弹目相对距离,r为R在惯性坐标系水平面上的投影,即r=Rcosε。
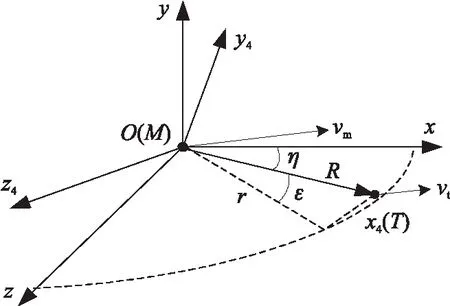
图1 弹目三维运动关系
导弹和目标的相对运动方程可以描述为[15]
(1)
式中:at,y4,am,y4和at,z4,am,z4分别为目标和导弹的加速度在视线坐标系Oy4轴和Oz4轴上的分量。
根据假设①和假设②以及导弹质心运动的动力学方程,可得导弹加速度在速度坐标系下的分量:
(2)
式中:m为导弹质量,g为重力加速度,θm为导弹弹道倾角,Fy和Fz分别为升力和侧向力。
(3)
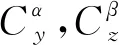
导弹在飞行中舵偏角对升力和侧向力的贡献相比攻角和侧滑角较小,因此可将其视为小量[16]。
结合式(1)和式(2),建立弹目相对运动方程:
(4)
式中:
(5)

根据导弹动力学方程,考虑主要因素,将次要因素视为不确定性的原则,构建导弹动力学模型为
(6)
(7)

以纵向平面为例,制导末端导弹和目标速度矢量间的夹角为导弹攻击角度θd,θd与终端视线角ε(tf)成一一对应关系,即
(8)
式中:θt为目标航迹倾角。
因此,攻击角度约束问题可以转化为终端视线角约束问题。
(9)
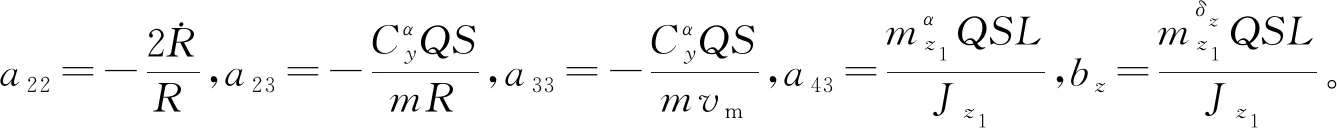
导弹在飞行过程中,目标大幅机动、导弹自身的不确定性以及外界干扰等因素可能导致控制幅值变大,达到执行机构约束上限,出现控制量饱和的现象,饱和问题会使系统的动态品质变差,导致控制性能下降甚至破坏系统稳定性,进而导致系统崩溃,因此在制导控制一体化设计中有必要考虑执行机构饱和的问题。考虑输入饱和问题,制导控制一体化俯仰通道设计模型(9)可重写为
(10)
式中:sat(δz)为俯仰舵实际舵偏角,其定义为
(11)
式中:δz,max为δz的已知上界,即最大舵偏角。
实际控制律sat(δz)与控制指令δz存在突变的尖角|δz|=δz,max,为使反演设计方法能够应用于制导控制指令的设计,对饱和函数光滑处理[17]:
(12)
令dz=sat(δz)-g(δz),则:
sat(δz)=dz+g(δz)
(13)
|dz|≤δz,max[1-tanh(δz/δz,max)]=0.238δz,max
(14)
因此dz是有界的。结合式(10)、式(13),可得考虑输入饱和的制导控制一体化俯仰通道设计模型:
(15)

参考俯仰通道设计模型,结合式(4)和式(6),建立制导控制一体化偏航通道设计模型:
(16)
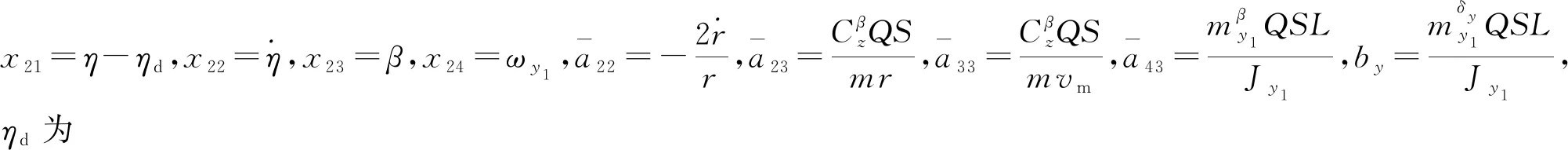
根据式(6)建立制导控制一体化滚转通道模型:
(17)
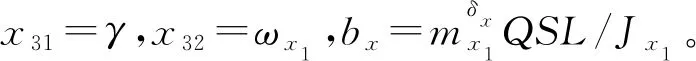
1.2 相关定义与引理
为后文公式推导和分析方便,引入如下相关定义和引理。
定义1为书写简便,定义符号[x]a=|x|asgn(x),其中,sgn(*)为符号函数,且sgn(0)=0,a为实数。

(18)
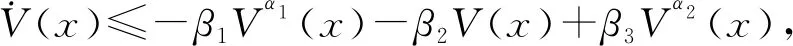
(19)
式中:θ1∈(0,β1),θ2∈(0,β2)。收敛域满足:
Ω={x|θ1Vα1-α2(x)+θ2V1-α1(x)<β3}
(20)
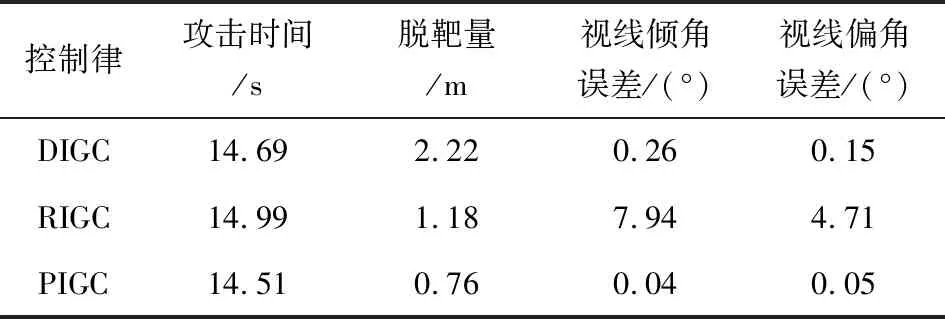
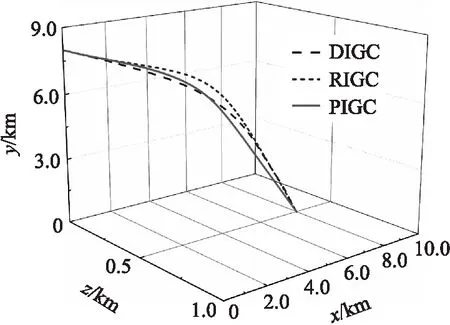
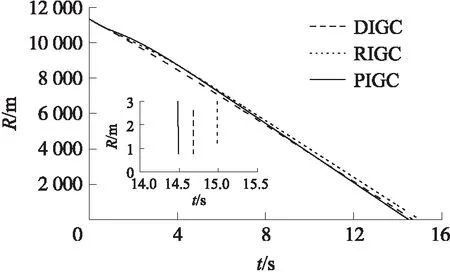
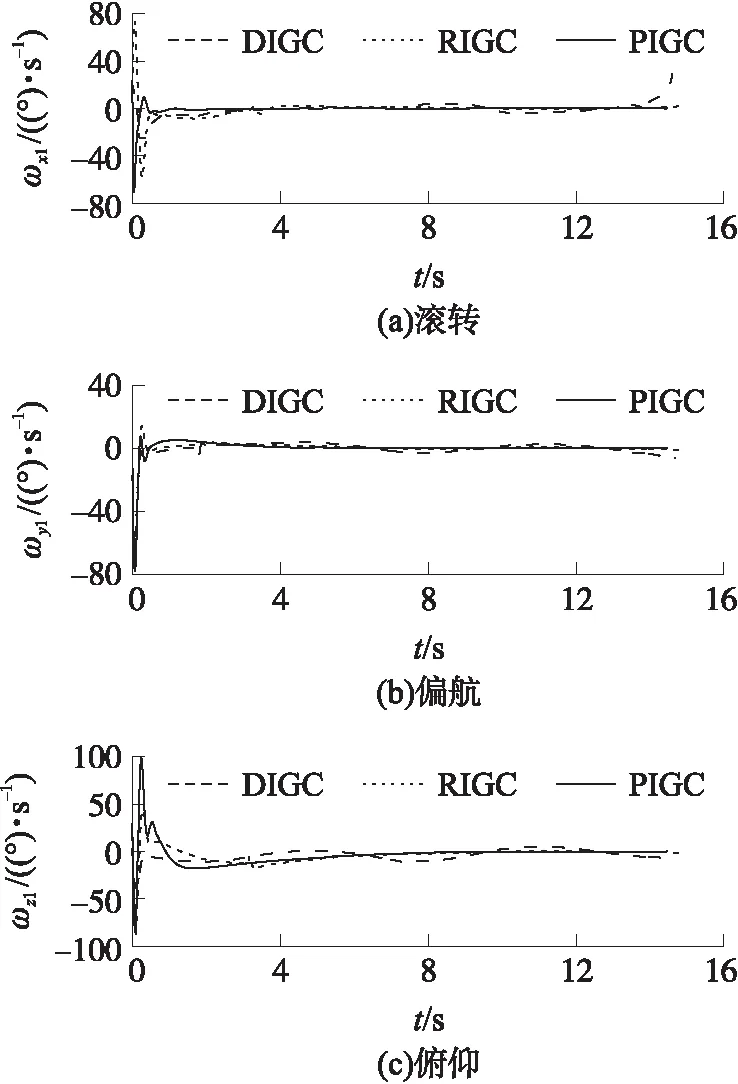
引理3[20]对任意实数xi,i=1,2,…,n,存在实数a(0 (21) 成立。 引理4[21]假定V(*)和χ(*)为定义在[0,tf)的光滑函数,且V(t)≥0,N(χ)是一个Nussbaum增益函数,若满足不等式: 式中:K>0,P>0,M>0,ψ(t)>0,则V(*)和χ(*)在[0,tf)是有界的。 制导控制一体化俯仰通道设计模型(15)中含有建模误差和不确定性。现有文献一般采用滑模控制的鲁棒性来应对模型的不确定性,或设计自适应律来估计模型的不确定性,但这些方法会引起控制量的抖振现象,且参数选取需已知不确定性上界。针对该问题,采用文献[22]提出的有限时间收敛干扰观测器对模型中的不确定项进行估计: (22) 针对非线性饱和问题,引入辅助系统: (23) 式中:δz,c为俯仰通道舵偏角控制指令,μ1>0。则俯仰通道一体化设计模型可写为 (24) 制导控制一体化设计模型(24)具有严格的反馈结构,因此,可以采用反演控制结合终端滑模控制进行设计。具体设计过程如下。 ①定义带攻击角度约束项的非奇异终端滑模面: s11=x12+ρ1x11+ρ2φ(x11) (25) 式中:ρ1>0,ρ2>0。 (26) 对式(25)微分得: (27) 式中: 结合式(24)和式(27),可得: (28) 设计虚拟控制律: (29) 式中:0 为避免对控制律求导产生微分膨胀问题,同时保证系统有限时间快速收敛性,设计如下一阶非线性滤波器: (30) 式中:y11=x13,d-x13,c,x13,d(0)=x13,c(0),τ为滤波器时间常数。 ②定义滑模面: s12=x13-x13,d (31) 设计虚拟控制律: (32) 设计一阶非线性滤波器: (33) 式中:y12=x14,d-x14,c,x14,d(0)=x14,c(0)。 ③定义滑模面: s13=x14-x14,d (34) 设计虚拟控制律: (35) 设计一阶非线性滤波器: (36) 式中:y13=x15,d-x15,c,x15,d(0)=x15,c(0)。 ④定义滑模面: s14=g(δz)-x15,d (37) 对s14求时间导数,得: (38) 式中: (39) 设计控制律δz,c: (40) 定理1对于系统(24),设计如式(40)所示的一体化制导控制律,使俯仰通道闭环系统状态x11和x12在有限时间内收敛至原点的一个较小邻域内。 证明由式(25)~式(40)可得: (41) (42) (43) (44) (45) (46) (47) 构造Lyapunov函数: (48) 微分得: (49) 基于Young不等式可得: (50) 式中: (51) 式(50)可写为 (52) 结合引理3可得: (53) 式中:ζ=ζ1+ζ2。 由于V1≥0,因此式(53)可写为 (54) 对式(54)两边同时积分可得: (55) 由引理4可知,V1和χ1是有界的,更进一步s1,s2,s3,s4,y1,y2,y3均有界。由式(53)可以得到如下2种形式: (56) (57) 对于式(56),若k-(ζ/V1)>0,则根据引理1可知,V1是有限时间收敛的,收敛域为 (58) 对于式(57),与式(56)分析类似,V1可有限时间收敛至区域: (59) ①|x1|≥δ,式(25)可写为 (60) 定义Lyapunov函数: (61) 对式(61)求导并将式(60)代入,得: (62) 合理选取参数k1,k2,使ϑ1≤δ,则x1的收敛域为 |x11|≤max{ϑ1,σ}=δ (63) 结合式(25)可得x12的收敛域: |x12|≤ρ1|x11|+ρ2|x11|b+|φ1|≤k1δ+k2δb+φ (64) ②|x11|≤δ,式(25)可写为 (65) 综上所述,x11和x12可有限时间收敛至原点的一个较小邻域: (66) 证毕。 偏航通道一体化制导控制律设计为 (67) 设计滚转通道一体化制导控制律: (68) 本节对所提制导控制一体化设计方法(PIGC)的有效性进行仿真验证。在惯性坐标系下,导弹和目标的初始位置分别设定为(0,5 000,0)和(8 000,1 000,500),导弹速度vm=800 m/s,导弹的初始弹道倾角、弹道偏角、攻角、侧滑角、滚转角、俯仰角速率、偏航角速率和滚转角速率分别为:θm0=-10°,ψv,m0=-5°,α0=10°,β0=5°,ωx,10=0.349 rad/s,ωy,10=-0.349 rad/s,ωz,10=0.524 rad/s。参考文献[24],导弹动力学参数如表1所示。 表1 导弹动力学参数 控制器参数选取为:ρ1=0.6,ρ2=1,b=3/5,c=0.5,δ=0.01,l11=l12=3,l21=l22=8,l31=l32=20,l41=l42=15,m11=m12=33,m21=m22=12,m31=m32=10,m41=m42=10,μ1=μ2=μ3=5,n21=n22=12,n31=n32=10,n41=n42=10,γχ1=γχ2=γχ3=0.001,τ1=τ2=τ3=0.1。 仿真中引入基于传统动态面控制的制导控制一体化设计方法(DIGC)和文献[24]提出的制导控制一体化鲁棒设计方法(RIGC)。设定Δα=Δβ=Δγ=0.2sint,Δωx1=Δωy1=Δωz1=sint,舵偏角的变化范围为[-10°,10°],期望视线倾角和偏角分别为-60°和0°。假设导弹的转动惯量存在0.1sin(0.2πt)的不确定性,气动力矩和力矩系数存在0.2sin(0.2πt)的不确定性。 仿真结果如表2和图2~图8所示。 图8 舵偏角曲线 表2 不同一体化制导控制律的仿真结果 图2 弹道轨迹 由图2可以看出,在3种一体化制导控制律的作用下,导弹都能平稳向目标飞行,弹道均较为光滑。由图3和图4可以看出,3种一体化制导控制律都能使弹目视线角ε和η逐渐收敛至期望值εd和ηd附近。其中,PIGC的收敛速度最快,体现了其有限时间快速收敛特性。DIGC和RIGC的弹目视线角在制导末段有一定的发散趋势,尤其是DIGC发散较为明显。这主要是由于PIGC采用扩张状态观测器对系统扰动和不确定进行了补偿,增强了系统的鲁棒性。而在制导末段DIGC和RIGC自身的鲁棒性不能有效对抗干扰,因此产生发散现象。由图5可以看出,3种一体化制导控制律的脱靶量,PIGC最小,RIGC次之,说明PIGC具有较高的制导精度。 图3 弹目视线倾角曲线 图4 弹目视线偏角曲线 图5 弹目相对距离曲线 由图6和图7可以看出,在PIGC和RIGC的作用下,导弹攻角、侧滑角、滚转角以及姿态角速度能够有限时间收敛至0附近,且PIGC收敛速度更快,收敛精度更高,而DIGC有一定的发散现象。由图8可以看出,PIGC的3个通道的舵偏角均没有超过最大限幅,且在后期均逐渐收敛至0附近。这是由于PIGC对输入饱和问题进行了考虑和处理。DIGC和RIGC的俯仰和偏航通道舵偏角在制导初段都达到了幅值上限。 图6 攻角、侧滑角和滚转角曲线 图7 角速度曲线 表2给出了采用3种不同的一体化制导控制律下,攻击时间、视线角偏差和脱靶量的仿真结果,可以看出,与DIGC和RIGC相比,PIGC的攻击时间、视线角偏差和脱靶量均最小,具有较高的制导精度和角度约束精度。 综合2种仿真情形的仿真结果分析,可以得出结论:在不同攻击角度约束条件下,PIGC都能以期望的攻击角度精确命中目标,脱靶量在1 m以内。并且能使弹目视线角和攻角等状态变量有限时间快速收敛,保证舵偏角在设定的幅值范围内变化。相比DIGC和RIGC,PIGC能以更短的时间、更小的脱靶量和更高的角度约束精度命中目标,且其状态变量的收敛速度更快。仿真结果表明了PIGC的有效性和优越性。 本文针对攻击角度约束、输入饱和和模型不确定性等问题,提出了一种有限时间收敛的制导控制一体化三通道独立设计方法。通过理论分析和仿真验证,有如下结论: ①所提制导控制一体化算法能够实现系统状态的有限时间收敛。在不同的攻击角度约束条件下,都能保证导弹以期望的攻击角度精确命中目标。相比现有制导控制一体化算法具有更高的制导精度和更好的收敛性能。 ②采用有限时间干扰观测器对模型不确定性进行估计和补偿,有效提高了制导控制系统性能。 ③所提制导控制一体化算法对输入饱和问题进行了有效处理,能够保证舵偏角的变化不超过设定的范围。
2 制导控制一体化设计
2.1 俯仰通道控制器设计与稳定性分析
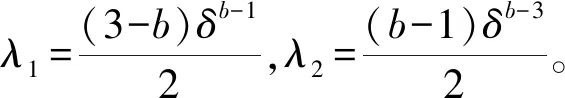


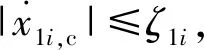
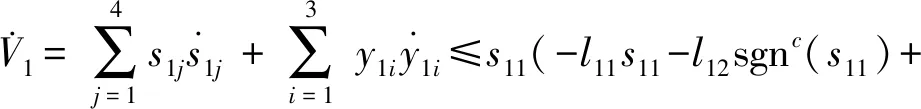




2.2 偏航和滚转通道控制器设计

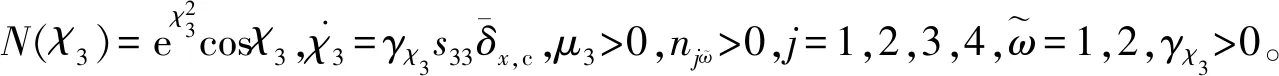
3 仿真分析





4 结论
