基于极限学习机的杀爆战斗部末弹道参数优化研究

2021-10-08王传婷

弹道学报 2021年3期

汪恒,何源,何勇,郭磊,王传婷,徐涛

(南京理工大学机械工程学院,江苏南京 210094)

杀伤面积能综合反映出破片速度、质量和空间分布以及战斗部落速、落角、炸高等终点弹道因素对威力的影响,是杀爆战斗部毁伤威力的重要指标之一[1]。所以在战斗部指标设计过程中,获得更大的杀伤面积是战斗部设计者关注的重点,因此对杀伤面积的求解以及末弹道参数的最优化处理显得尤为重要。

目前可以通过数值仿真计算战斗部杀伤面积[2],但仿真计算运算周期较长,很难通过此方法得到最优的末弹道参数。另一种求解方式是采用理论模型对杀伤面积进行计算,通过概率密度函数描述破片的空间分布,得到杀伤面积函数[3],将杀伤面积函数看做优化问题的目标函数[4],利用传统优化方法对战斗部结构进行最优化运算。但事实上破片分布密度是不确定的,利用概率密度函数描述破片空间分布会导致计算结果不准确[5],特别是对破片空间分布不满足概率密度函数的战斗部来说,这种方法并不实用[6]。有的学者利用射击迹线描述破片飞散实际轨迹[7],避免了上述方法描述破片空间分布的不准确性。

本文基于合理假设,利用破片的初始状态计算破片落点,统计地面网格中的有效破片数,对战斗部在不同末弹道参数下的杀伤面积进行了准确计算,但以上方法利用了地面微元内有效破片数这一统计量,使计算得到的地面微元内的杀伤概率为离散值,导致杀伤面积公式无法作为优化问题的目标函数。目前常采用枚举法处理上述问题,但枚举法计算量巨大,因此本文利用极限学习机(extreme learning machine,ELM)描述末弹道参数与杀伤面积之间的复杂关系,对末弹道参数进行快速枚举。

1 杀爆战斗部毁伤计算模型

1.1 动态条件下破片飞散

为便于建模分析,做如下假设:①破片在飞散过程中只受到空气阻力的作用;②破片在空间中的飞行轨迹为直线;③不考虑攻角对杀伤面积的影响。

建立杀爆战斗部随动坐标系Oxyz,如图1所示。图中,战斗部起爆点位置O为坐标系原点,d为战斗部头部到起爆点的距离,v0为破片静态初速,φv为破片静态飞散方向角,vc为战斗部落速,dA为A位置破片与战斗部头部的距离,R为A位置与战斗部轴线的距离,点Axy为点A在Oxy平面的投影,θ为OAxy与Ox轴的夹角。

利用速度矢量和得到破片动态飞散方向角φ以及破片动态飞散速度v:

(1)

(2)

考虑战斗部形状,某一破片A飞散运动方程在Oxyz坐标系中各个轴上的投影为

(3)

建立地面坐标系O′x′y′z′,其中O′为原点O在地面上的投影,O′x′y′为地面,O′x′轴为战斗部速度水平分量的方向。将图1中破片的初始状态以及炸高H和落角α引入到该坐标系中,得到如图2所示的破片飞散模型。

图1 破片飞散初始状态

图2 破片飞散模型

A位置的破片在O′x′y′z′坐标系中的初始运动方程为

(4)

确定方程(4)中角度θ、落角α、炸高H,破片位置到战斗部轴线的距离R,以及破片动态飞散方向角φ和破片动态飞散速度v就能得到破片落点。

1.2 杀伤面积模型

杀伤面积是地面上任意一点A′(x′,y′)的杀伤概率P(x′,y′)与微元面积ΔS=ΔxΔy的加权面积,其中Δx和Δy分别为地面笛卡尔网格在x′方向与y′方向上的增量,杀伤面积可表示为

S=∑P(x′,y′)ΔS

(5)

ΔS为单个目标所占平均面积,目标相同时为定值;微元面积内杀伤概率P(x′,y′)按下列公式计算:

(6)

式中:Ns为目标毁伤时最小命中破片数,人员目标为1枚;NK为微元面积ΔS内满足杀伤准则的破片数,本文采用杀伤动能准则作为模型的杀伤准则,破片在到达目标时动能超过78.4 J,则认为该枚破片能够达到对人员目标的杀伤作用[5],破片速度衰减规律可由以下公式得到[8]:

(7)

式中:vp为破片存速,rf为破片飞行距离,mp为破片质量,Hx是与破片形状有关的系数。ST为目标的暴露面积,通过以下公式计算[9]:

(8)

2 基于极限学习机的模型

ELM是一种单层隐含前馈神经网络(SLFN)的学习算法,这种算法可以自适应地设置隐层节点数,并随机分配输入权值与隐层阈值,隐含层和输出层之间的连接权值通过求解方程组一次完成。由于ELM不需要调整网络输入权值和隐藏偏差,使其具有学习速度快、泛化性能好等优点[10]。与通过理论模型计算杀伤面积不同,ELM通过隐藏节点直接描述末弹道参数与杀伤面积数值之间的关系,对杀伤面积进行求解。

现将随机选取的N组训练集引入到具有L个隐藏节点的SLFN中,训练集中末弹道参量输入矩阵X和对应的杀伤面积输出矩阵Y为

(9)

式中:n为末弹道参数组号。将权值和偏差考虑到末弹道参量输入矩阵中,根据任意的概率分布函数,随机生成输入矩阵相对于隐含层节点的权值wi和偏差bi,表示为

(10)

式中:win1,win2和win3分别为第n组末弹道参数对第i层隐含层的权重;bin为第n组末弹道参数对第i层隐含层的偏差。当以wiX+bi为自变量,ELM中激活函数采用sigmoid函数时,可以得到ELM第i个隐含层节点输出hi为

(11)

此时,可以得到ELM的输出为

(12)

(13)

(14)

式中:βi为第i个隐含层对输出层的权重,权重值可以通过隐含层输出矩阵M(X)和杀伤面积结果得到:

βi=(MT)+·YT

(15)

文献[11]表示只要隐藏节点的数目足够,且当激活函数在任何时间间隔无限可微时,ELM的其余参数不需要调整。本文采用决定系数Ω2对学习结果进行评价:

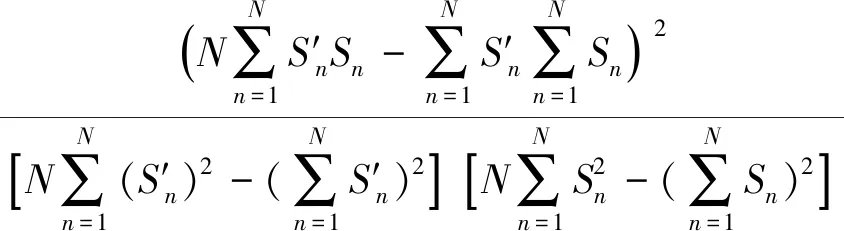
(16)

式中:S′n为第n个样本的预测值;Sn为第n个样本的真实值。决定系数区间在[0,1]内,且越接近1,表明模型的性能越好,反之越差。利用ELM求解杀伤面积的计算流程,如图3。图中,X1为训练集输入,Y1为训练集输出,X2为测试集输入,Y2为测试集输出,Xg1,Yg1和Xg2分别为X1、Y1和X2归一化后的结果,Y′g1为测试集输入X2在ELM计算后的结果,Y′2为Y′g2反归一化后的结果。

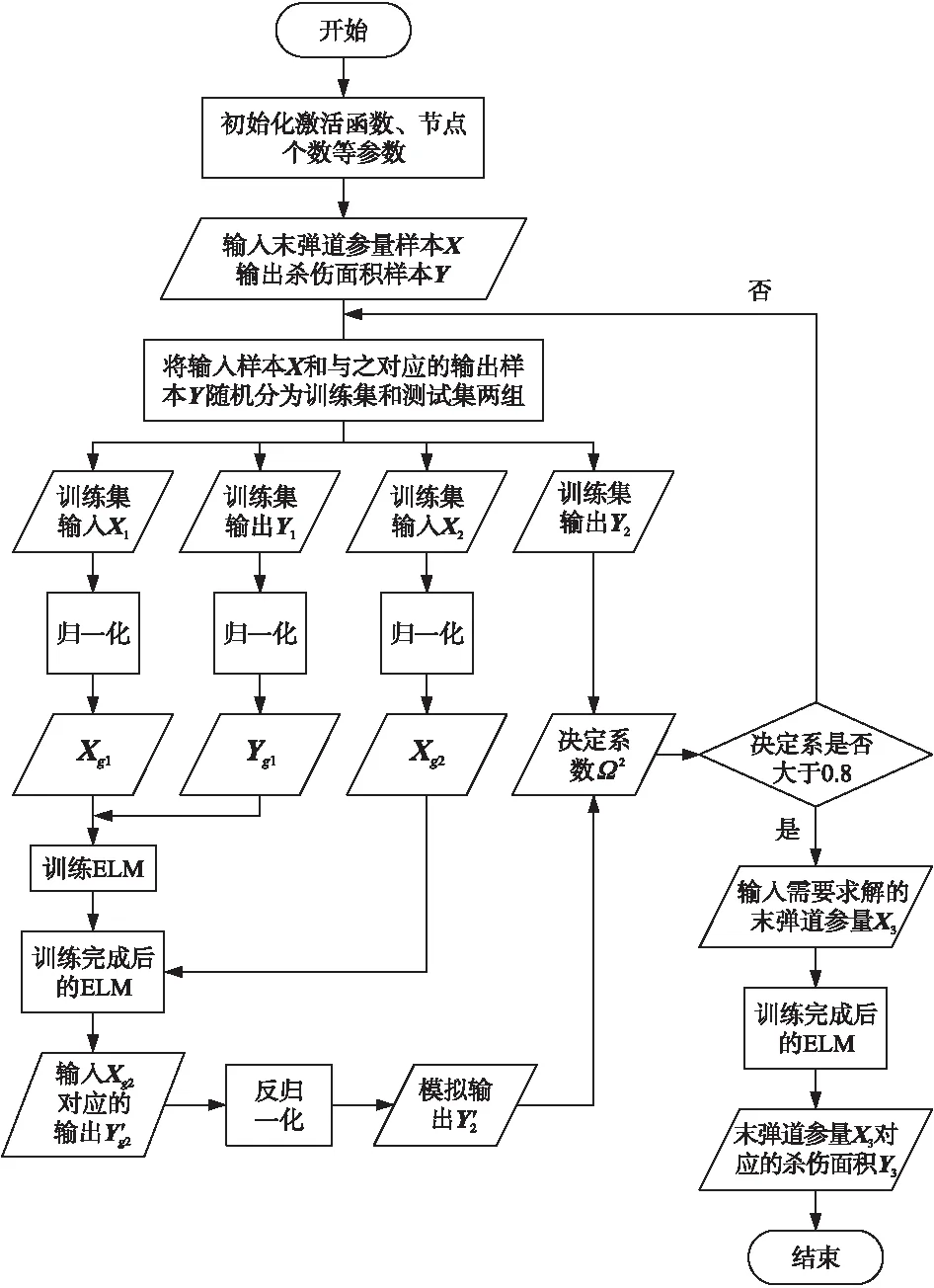
图3 ELM计算流程图

3 结果与分析

3.1 破片飞散参数

文献[12]采用文献[13]中求解杀伤面积的方法得到了与试验结果符合较好的结果。说明文献[13]中计算结果可靠,本文模型求解的杀伤面积与文献[13]中数据的对比结果如表1。

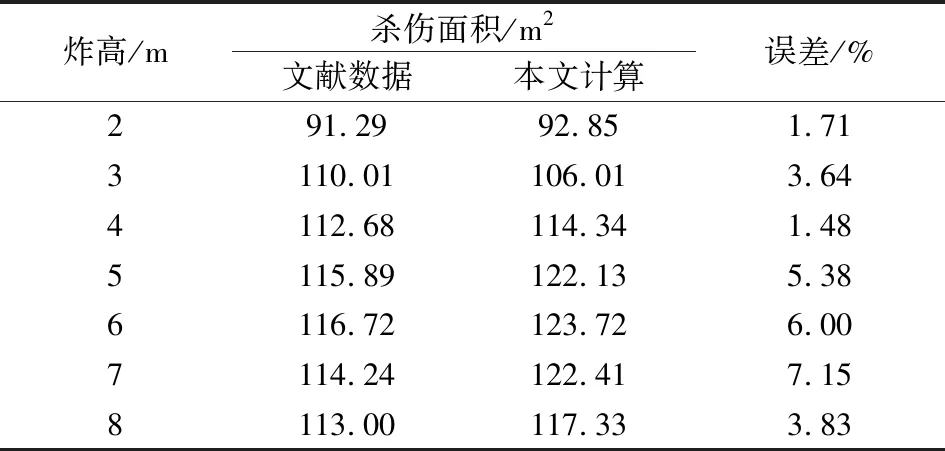
表1 计算结果与文献结果比较

由表1可知,本文模型求解结果相对于文献中数据的误差较小,说明本文ELM方法用于计算杀伤面积合理可靠。利用文献[14]中战斗部静止端点起爆,钨球预制破片初速和飞散方向角的数值仿真结果作为本文的破片飞散参数,破片飞散参数如图4。

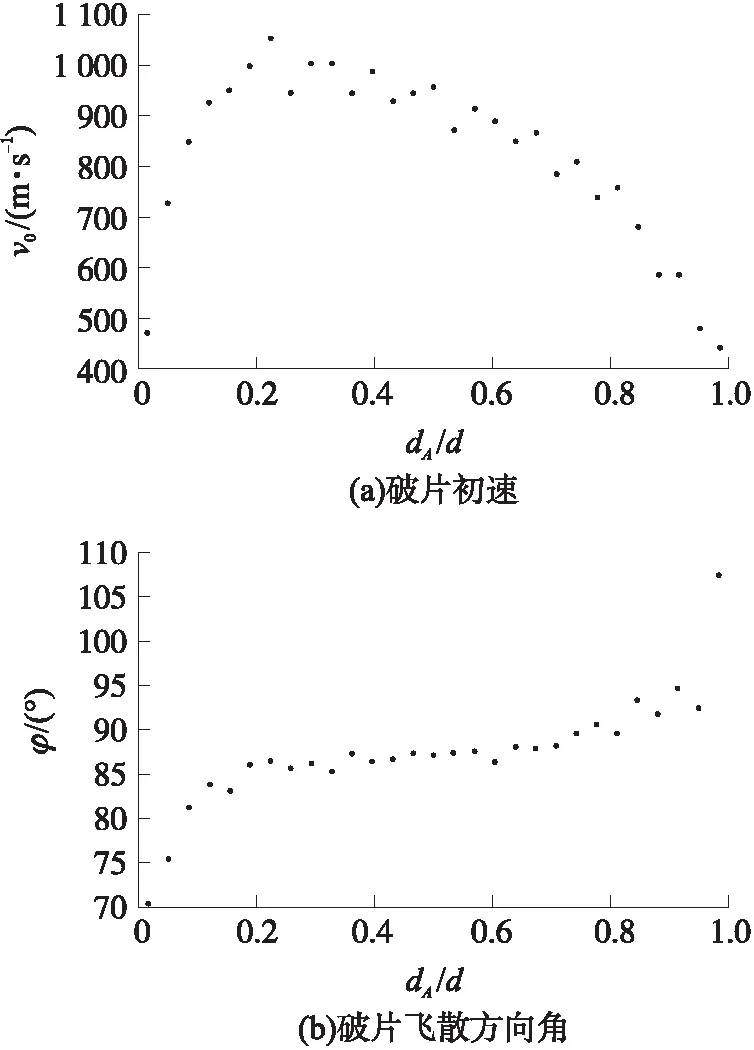
图4 破片飞散参数

战斗部尾部端点起爆时,战斗部头部到起爆点的距离d表示的就是战斗部总长度。此外,下文中通过本文建立的杀伤面积模型得到的结果,针对的都是文献[14]中提到的飞散参数,如图4所示的钨球预制破片战斗部。

将初始参数以及不同的末弹道参量代入到上文中的杀伤面积模型中,得到战斗部落速每隔10 m/s,从10 m/s变化到250 m/s,落角每隔5°,从60°变化到90°,炸高每隔1 m,从3 m变化到9 m时的杀伤面积,为ELM提供1 225个源数据。

3.2 影响ELM求解结果的因素

在用ELM求解杀伤面积之前,需要讨论ELM模型中激活函数类型和隐藏节点个数对求解精度的影响,使计算选取的激活函数和隐藏节点个数符合精度要求。除了上文提到的sigmoid激活函数,常用的激活函数还有正弦函数和hardlim函数,当输入为负,hardlim函数值为0,否则函数值为1。改变ELM中隐藏节点个数,利用3种激活函数得到结果的决定系数如图5所示。

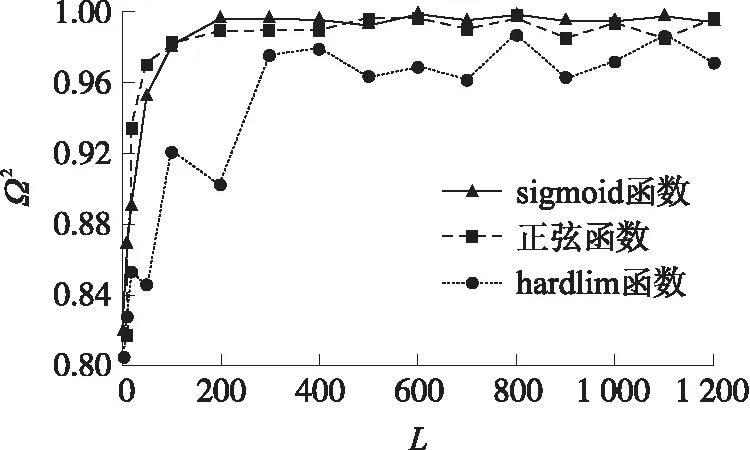
图5 决定系数与节点个数的关系

从图5中可以发现,当ELM隐藏节点个数到达200个后,sigmoid函数和正弦函数得到结果的决定系数已达到0.98以上,且sigmoid函数得到的决定系数较正弦函数高,而hardlim函数得到结果的决定系数较前两种函数低。不仅如此,在改变决定系数个数时,hardlim函数得到的决定系数值波动较大,而sigmoid函数结果稳定性较好。因此,本文利用sigmoid激活函数求解杀伤面积,为在保证精度的前提下加快求解速度,隐藏节点个数选择300个,此时ELM训练结果误差为

(17)

得到预测值S′n与真实值Sn的误差如图6。图中,f为ELM训练结果误差的出现频次。

图6 ELM误差

图6结果表示,激活函数为sigmoid函数,隐藏节点个数为300个时,真实值与ELM学习结果之间的误差绝大部分在10%以内,极少出现大于10%的误差,ELM学习结果有效且可信。

3.3 通过ELM优化末弹道参数

随机将部分数据作为学习集输入ELM,对ELM进行训练,再通过训练完成后的ELM对落速每隔0.1 m/s从10 m/s变化到250 m/s,落角每隔2.5°从60°变化到90°,炸高每隔0.1 m从3 m变化到9 m时的杀伤面积进行计算,ELM可在极短时间之内计算出上述1 903 993种参数组合的结果,图7展示了落角分别为60°,70°,80°和90°时ELM的计算结果。

图7 ELM计算结果

从图7中看到,落角为60°和70°时,炸高和落速的变化引起的杀伤面积变化很小,杀伤面积图像几乎为一个平面;但当落角较大,特别是落角为90°时,从图中颜色的变化可以发现,随着落速增大,杀伤面积在达到最大值前迅速变化,之后变化缓慢,随着炸高增大,杀伤面积在达到最大值之前缓慢变化,而后变化迅速。

这是因为落角较小时,战斗部远离地面的一侧的破片大多飞向空中,由于此时能造成毁伤的破片较少,不论如何改变落速或炸高,有效破片仅在靠近地面一侧的破片中增多;而落角较大时,原先远离地面一侧的破片也会形成有效杀伤,此时再改变落速或者炸高,有效破片不论是远离地面的一侧,还是在靠近地面的一侧都会增加,增量更大,因此此时落速和炸高对杀伤面积的影响越大。

上述现象表明:为减小引信起爆高度误差对杀伤面积的影响,引信起爆时,战斗部的落速应较最佳落速更大,炸高应较最佳炸高更小。

从图7结果还可以发现,当战斗部落角为60°,炸高在7～9 m,落速在10～50 m/s区域内时对应的杀伤面积更大;但是当落角变为70°,炸高在3～5 m、落速在10～50 m/s区域内以及炸高在7～9 m、落速在150～250 m/s区域内时,都会出现较大的杀伤面积区域;落角为80°时,杀伤面积较大区域出现在炸高为3～5 m,落速在150～250 m/s区域内;但落角为90°,杀伤面积较大区域却出现在了炸高在3～5 m,落速在10～50 m/s的区域内。利用ELM得到各个落角状态下杀伤面积以及对应的落速和炸高,如表2所示。

表2 落角为定值时ELM得到的最优末弹道参数

由表2结果可以看到,通过合理优化落速和炸高,随着落角增大,战斗部最大杀伤面积增加,最大杀伤面积对应的落速和炸高可以直接通过ELM得到。但从落角、落速和炸高三个方面同时评估杀伤面积时,通过ELM得到杀伤面积如表3所示。

表3 ELM得到的最优末弹道参数

通过比较ELM解得的最优末弹道参数与源数据杀伤面积所对应的末弹道参数发现,虽然两者得到的炸高相同,落角相差2.5°,仅落速相差较大,但通过ELM得到的最大杀伤面积明显优于源数据结果,说明ELM结果能够有效改善战斗部杀伤面积。

ELM方法不仅结果优于源数据结果,其计算速度也比直接利用杀伤面积模型计算源数据更快,两者计算耗时如表4所示。

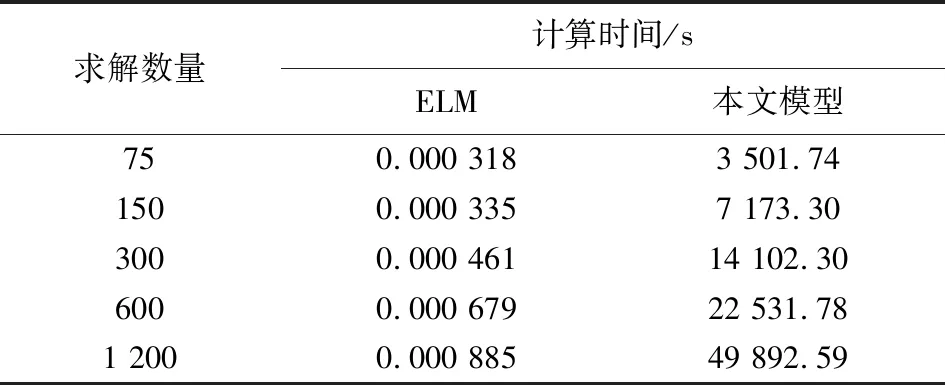
表4 ELM和本文建立的杀伤面积模型计算时间

由表4可知,虽然ELM求解时间随着求解数增加而增加,但其所耗时间都远远小于1 s,直接利用杀伤面积模型进行求解1 200个结果需要花费近14 h。可见,随着求解数量的增加,ELM求解速度优势越明显。

3.4 ELM对大落速战斗部的优化方案

文献[14]采用的是火箭弹战斗部,落速较低,而很多战斗部的落速要高很多,现研究某战斗部在较大落速时的最优化方案。某高落速战斗部的破片初速和飞散方向角沿轴向分布如图8所示。

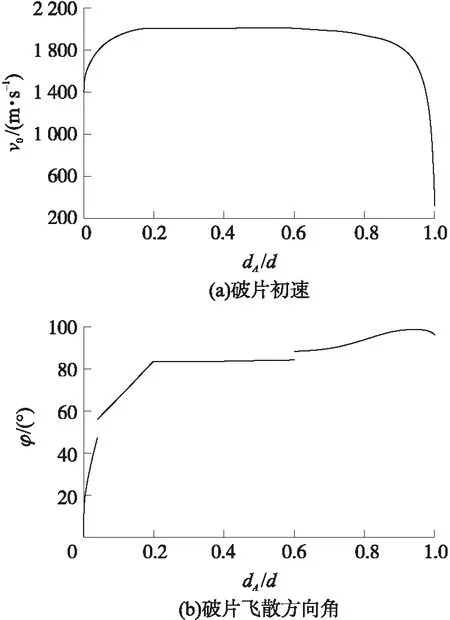
图8 破片初速和飞散方向角沿轴向分布

该战斗部外轮廓不光滑,有2个断点,因此破片飞散方向角存在2个突变的位置。

落角为90°,炸高每隔1 m从25 m变化到40 m,落速每隔10 m/s从400 m/s变化到600 m/s,利用计算杀伤面积模型求解杀伤面积的336个结果;炸高每隔0.05 m从25 m变化到40 m,落速每隔0.05 m/s从400 m/s变化到600 m/s,利用学习完成的ELM计算杀伤面积的1 204 301个结果,如图9所示。