跨越数形

吴安

摘要：数学是研究数量关系（数）与空间形式（形）的学科，聚焦于数和形有效的统一。以数论形，形有数时更入微，让数的量化研究形的直观;以形表数，数有形时析本质，让形的表象具化数的精确;数形结合，实现数的可视化和形的数量化，形数互联提思维。

关键词：以数论形 以形表数 数形互联 持续发展

引言

虽然数形结合思想是小学阶段学习中最常用的数学思想之一，但是实际教学中，教师更偏重以形解数，即基于几何直观，利用图示等直观的特性，探究已知条件和问题之间的数量关系，辅助解决实际问题。而图形现象算法化，数形结合相印证的课堂实践相对甚少，《分数乘分数》一课是一个很好的载体，本文试图从数形结合角度出发，从以数论形、以形表数和数形结合三方面对《分数乘分数》一课进行解析和架构，探索数形结合思想在课堂教学中的实践与应用。

一、以数论形，形有数时更入微

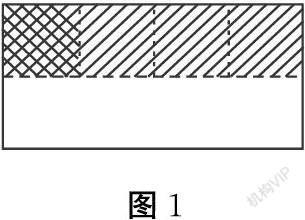
数学抽象于现实世界，对数学的学习能不断完善学生已有认知的知识结构体系，因此我们的数学教学和学习具有抽象性、关联性及延展性。开展《分数乘分数》教学的基础是学生已经掌握分数与涂色表示的一一对应关系以及求一个数的几分之几是多少可以用乘法计算等，为实现从静态观察到动态生成，突出分数乘分数产生的过程，展示思维思考层次。教学从一张纸的二分之一展开，“你想到哪个分数，为什么？”接着再出示涂色二分之一的四分之一（图1）。

让学生想想这时候又该用哪个分数表示，有的学生说是四分之一，有的学生说是八分之一。此时产生认知冲突，引发思考：同一个涂色部分为什么会用两个分数表示，这两个分数之间有什么联系？学生不难发现单位“1”不同，长方形二分之一的四分之一就是这个长方形的八分之一，继而记录二分之一的四分之一是八分之一;带领学生经历图形产生的过程之后，出示第二幅图（图2）。

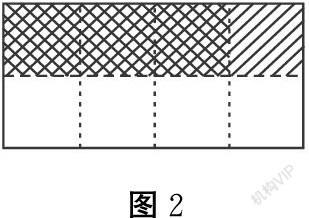
这时候的涂色部分可以用哪些分数表示，它们之间有什么联系？得出二分之一的四分之三是八分之三;接着让学生通过图形分析的含义列出算式，认识到从简单的涂色开始研究出新的分数乘分数的内容，也让学生感受到以数论形可以让图形呈现的信息更细致，促进学生感知知识产生过程，架构分数乘分数的概念本质，接着出示（图3）。

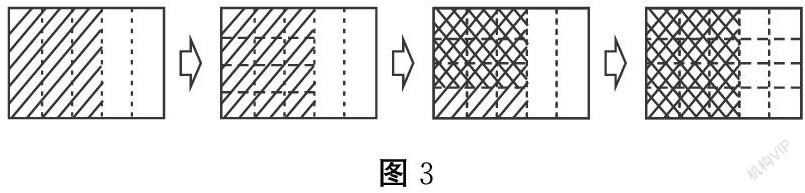
让学生再来说说这幅图表示什么意思。算式呢？交流明白五分之三的四分之三是二十分之九，即五分之三乘四分之三等于二十分之九。相较于前面的分法，这个稍有难度，只为进一步提高学生以数论图的能力。

当回顾前面看图、识图的过程，提问今天学习分数及涂色表示和以前学习的分数有什么不同时，学生经历由扶到放，能够明白这其中还蕴含着分数乘分数的计算，也能切实感受到分数乘分数的本质其实就是“先分——先取——再分——再取”的过程。从图形的表象描述到数据的深入刻画，相信能够导向学生看形思数的思考方式，引导学生养成基于图形视觉感知的过程领悟数量关系的能力。

二、以形表数，数有形时析本质

数学的课堂教学不仅仅是知识的传授，还有数学学习方法的获取，从现象的感知到本质的探究是学习和认知向更高层次发展的过程，也是学生规律探究、结论生成、模型建构的渐进过程。通过前面以数论形的先见，根据已有经验或观察、或思考，学生不难发现分数乘分数的算法是分子相乘的积作分子，分母相乘的积作分母。但这只是表象的猜想，事实是否如此，我们需要进一步的验证，出示书本例子（图4）。

三分之二分别乘五分之一和五分之四表示什么意思？它们的结果是多少？你能通过画图验证吗？在开放的情境中自主探究数的运算与图示表征之间的关系，在“发现问题——提出猜想——举例验证——得出结论”的过程中，学生不仅能习得基础知识，还能获取数学学习的基本技能;此时追问：分数的分子相乘和分母相乘的积的结果表示什么？你能在图中指一指吗？（图5）

以形表数，从数据的运算到图形的表征，学生不仅能在探究的过程中明晰分数乘分数的算法，也能明白这样算的道理，即“先分——先取——再分——再取”的认知现象到“一分再分的积就是分母，一取再取的积即分子”算理的概念本质;也知道遇到问题如何思考，如何利用不完全归纳方法从表象抵达结论的实践。在教学中不断积累探究数学规律的基本活动经验，也不断促使学生挖掘结论背后的数学本质。

三、数形结合，形数互联提思维

数形结合，实际上是以数论形、以形表数、形数互联的紧密融合。这要求教师在教学过程中不断引导与渗透，启发学生由形的直观关联数的抽象，由数的抽象联想形的直观，使学生在探究中实现数形互化、相互映衬的数学学习思考能力的提升。

当探究分数乘分数的算法和算理之后，继而进行相应的练习，出示练一练（图6），看图说说算式的意思，并说说可以怎样计算。而后追问：在图中，分子相乘和分母相乘表示什么？你能在图中指一指吗？

聚焦于第2个算式，首先关注计算，比较一下，这个计算和前面遇到的分数乘分数有什么不一样的地方？我们计算时需要注意什么呢？建构和分数乘整数知识计算法则的联系，发现实际上我们可以先约分再计算，这样更简便;再次关注图形，这里的得数是十分之三，你还能在图中找出十分之三吗？约分计算和图示之间有什么变化？前面学生已经很好地掌握数的运算和图示表征算理之间的关联，但又遇含有约分的新情境，在辨析、对比中进一步感悟分数乘分数的运算、约分及算理之间的联系。至此，学生已经完全掌握分数乘分数的算法和算理;接着再出示试一试第1题，你能先约分再计算吗？试着算一算。汇报交流之后，追问：想一想，若是画图又该是怎样的？约分的过程呢？学生或画图尝试、或想象建构、或自由讨论，最后出示图示过程，尤其是第二个计算中进行两次约分过程（图7），约分的3乘4，即是12。再次进一步巩固算法、约分和算理之间的连接，让学生在不断深入中深度思考。

出示试一试第2题，前面学习的是分数乘整数，我们知道整数是特殊的分母为1的分数，你能用分数乘分数的方法计算下面各题吗？在计算之后交流分数与分数相乘与分数与整数相乘之间的联系，适时追问十一分之二乘三用画图表示是怎样的？和分数乘分数之间有什么不一样？（图8）

让学生在对比中发现分数乘分数和分数乘整数之间的区别与联系，构建从特殊的分数乘整数到一般的分数相乘相关联的知识结构体系。

以上教学设计虽主要针对分数乘分数的计算，但是关注的重点不仅仅是计算，更关注通过算法和算理之间的互通有无，有涉及约分的深入思考，有牵涉与整数相乘的区别的辨析。通过数形互化、形数结合，在教学实践中不断尝试和渗透，相信能够切实提升学生的高阶思维水平。

如何让学生积累基本活动经验，感受数学基本思想，如何发展学生的數学核心素养……不管还有哪些，一定是在一节节课堂中落地，这必将是一个长期的循序渐进的过程，本节课就是朝着这样的方向思考与践行的。课程标准中关于运算能力提出能正确运算、能理解算理并能简洁解决问题等三方面要求。可见会算只是基础，我们需要在教学实践中充分挖掘知识背后的方法与思想，而经历探究知识产生的过程，获得探究问题的思考方式就是这节课需要积累的数学经验的学习路径，数形结合的互通互联就是我们需要关注的数学思想。相信只有在一节节多角度、多维度、多深度的课的思索中，才能让学生形成持续发展的数学核心素养。