自重荷载下非均匀支撑板式无砟轨道静态响应

蒋红光，刘舜，李宜欣，李昕亮，薛志超，姚占勇†

（1.山东大学 齐鲁交通学院，山东 济南 250002；2.山东高速集团有限公司，山东 济南 250098）

经过10 多年的快速发展，我国已成为世界上高速铁路规模最大、运营速度最高的国家.列车的高速运行对轨道的平顺性提出了非常严格的要求，而路基作为轨道的重要支撑结构，需要为轨道提供平顺的几何形状.但是在实际工程中，路基往往会产生不均匀沉降[1-2]，考虑到扣件系统高度的调节极限，我国高铁设计规范要求普通路基段20 m 内的不均匀沉降不得超过15 mm.在自重荷载作用下，非均匀路基支撑将导致轨道结构附加应力增大，影响交通基础设施的耐久性.由于板式无砟轨道的整体刚度非常大，其轨面变形并非与路基不均匀沉降完全一致，轨下结构损伤往往具有很强的隐蔽性，一旦发展到轨道结构应力损坏，维修和更换难度非常大，因此需要充分评估非均匀支撑下的板式无砟轨道几何形态和力学响应.

对于路基不均匀沉降对上部结构和列车运行的影响，大多以理论研究为主.邹春华等[3]采用余弦函数表示路基不均匀沉降，基于连续弹性支承梁理论，得到了有砟轨道轨面沉降分布计算公式.吴仲伦[4]在研究路基冻胀引起的轨面不平顺时，基于有限元模型建立了具有一定初始隆起形状的路基，进而获得了轨道结构和钢轨对应的几何不平顺.Paixao 等[5]基于有限元模型，较为系统地研究了路基不均匀沉降波长和幅值对轮轨动力响应的影响，并基于安全性和舒适性要求提出了相应的控制指标.针对整体刚度更好的板式无砟轨道，陈仁朋等[6]研究了路基中长波不平顺下轨道板的受力，并基于抗弯疲劳强度允许值，提出了路基不均匀沉降的控制准则.由于路基沉降主要来自地基下沉，罗强等[7]研究了地基差异沉降模式、路堤高度等因素对路基面不均匀变形的影响，并建立了两者的映射关系.陈兆玮等[8-9]对不同类型板式无砟轨道系统的钢轨变形和桥墩沉降映射关系进行了理论推导，并获得了钢轨的变形区域与幅值.蒋丽忠等[10]建立了数值解析模型和有限元模型，研究了不均匀沉降发生在不同路桥位置处的钢轨变形形态与映射关系.何春燕等[11]进一步研究了路桥过渡段不均匀沉降与钢轨变形的映射关系，并应用于列车的动力学分析.肖威[12]、裴国史[13]等分别针对高速铁路和有轨电车线路建立了板式无砟轨道数值模型，分析了轨面变形、轨道结构应力与路基不均匀沉降波长和幅值的相关规律.徐庆元等[14]综合考虑了轨道不平顺、路基不均匀沉降、温度梯度和列车荷载的影响，基于混凝土底座疲劳破坏限值，提出高速铁路CRTSⅠ型板式无砟轨道的不均匀沉降限值为7 mm/20 m，但未研究其他沉降波长的影响.张克平等[15]建立了考虑轨道自重荷载的车辆-轨道动力学模型，分析了行车速度、路基不均匀沉降波长和幅值对车辆动力学性能的影响.

综上可见，当路基发生不均匀沉降后，轨道结构力学响应不仅受列车动载的影响，也与其自重荷载作用密切相关.而且，不同路基支撑条件下的轨道结构抗弯刚度也在很大程度上决定了变形和应力的传递.实际上，轨面的形态映射和力学响应是轨道结构参数与路基不均匀沉降型式共同作用的结果，Auersch[16]基于Winkler 地基上的单层弹性支承梁模型，指出轨道存在一个与轨道抗弯刚度有关的截止波数，决定了轨面的映射特征.现有研究大多集中在路基不均匀沉降对轨道结构应力状态的定性讨论，未能建立路基不均匀沉降与轨面变形和轨道结构受力状态的定量关系.本文通过建立高速铁路CRTSII 型板式无砟轨道-路基三维有限元模型，研究了典型路基不均匀沉降组合下的轨面映射特征，提出了考虑不均匀沉降波长的混凝土底座柔度，建立了基于柔度表征的轨面-路基几何形态映射、附加应力以及路基接触应力的相关关系，以定量评估非均匀支撑板式无砟轨道静力响应，提出敏感的不均匀沉降型式，并讨论了改变混凝土底座模量和厚度对提高轨面几何平顺性的效果.

1 数值模型

1.1 板式无砟轨道三维有限元模型

根据中国高速铁路广泛使用的CRTSII 型板式无砟轨道，建立了三维有限元模型如图1 所示.其中，模型总长60 m；钢轨采用UIC60 型，以连续的欧拉梁单元模拟；轨道板2.6 m（宽）×0.2 m（厚），CA 砂浆层（CAM）2.6 m（宽）×0.05 m（厚），混凝土底座3.25 m（宽）×0.3 m（厚），基层表层0.4 m 厚，采用六面体实体单元模拟.钢轨采用WJ-7 型扣件系统固定到轨道板上，以刚度为28.5 kN/mm 的垂直弹簧单元模拟.考虑到不均匀沉降的存在，当垂直接触压力降为零时，路基、混凝土底座、CAM 层和轨道板之间的界面允许分离.法向采用硬接触，切向接触由库仑摩擦模型模拟，接触面在开始相对滑动之前可承受临界切应力.模型底部为固定边界，四周采用对称约束并允许产生竖向位移U2.数值模拟的计算参数根据浙江大学物理模型试验取值[17]，见表1.

图1 CRTSII 板式无砟轨道断面图（单位：m）Fig.1 Section of the CRTSII ballastless track（unit：m）

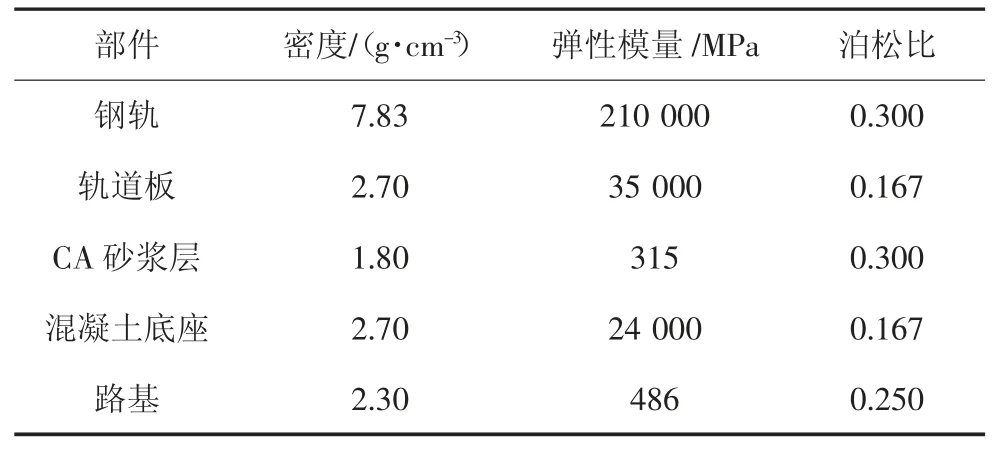
表1 数值模拟计算参数Tab.1 Calculation parameters of the numerical simulation

1.2 数值模型可靠性验证

浙江大学建立了全比尺的板式无砟轨道物理模型试验装置，并开展了列车轮轴作用下的扣件荷载分担比试验[18-19].作动器通过分配梁将荷载传递至两侧钢轨上，例如当分配梁分别置于5#扣件和4#与5#扣件之间时（见图2），模拟了列车轮轴分别移动至扣件上方和相邻两个扣件之间.作动器分级施加荷载50～200 kN，增量为50 kN.千分表固定在轨道板表面，以记录各级荷载下扣件系统的压缩变形，通过扣件刚度可换算得到分担到的荷载值.图2 给出了各个扣件在分级载荷下的实测变形.当轴向载荷直接施加在扣件上方时，约5 对扣件分配轴载.轴向载荷从50 kN 增加到200 kN 时，扣件的最大变形从0.3 mm 增加到1.2 mm.当轴载作用在两个相邻扣件之间时，大约6 对扣件分配轴载，钢轨最大变形量也从0.3 mm 增加到1.2 mm.数值模拟结果如图2 中实线所示，在两个不同的位置施加轴载时，均与物理模型试验结果吻合较好.因此，后文将采用该三维有限元模型进一步研究路基不均匀沉降作用下板式无砟轨道结构的形态映射和附加应力特征.

图2 扣件变形的试验和数值模拟结果Fig.2 Comparisons of fastener deformation between experimental and numerical results

1.3 不均匀沉降模型

有限元模型中，路基不均匀沉降的波长和幅值特征采用余弦函数表示，见式（1）.

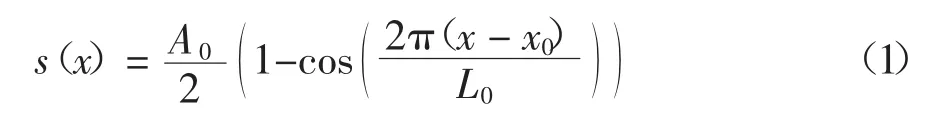
式中：s（x）是路基沉降；A0和L0分别是沉降幅值和波长；x0是路基沉降发生的初始位置.数值模拟中选取不均匀沉降的波长为5～40 m，间隔5 m；沉降幅值为5～40 mm，间隔5 mm，共计64 种组合.在对路基施加不均匀沉降之前，首先对模型进行地应力平衡，使其初始变形为零.随后，路基顶部节点向下移动以生成不均匀沉降边界，如图1 所示.

2 轨道结构几何映射特征

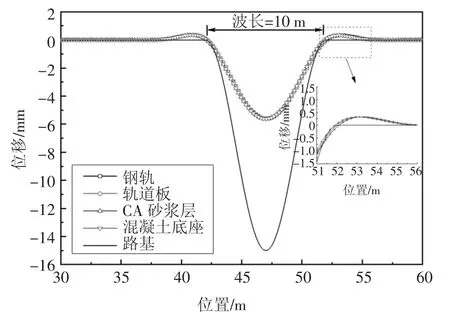
图3 15 mm/10 m 沉降下轨道结构的位移Fig.3 Displacement of track structure under uneven settlement of 15 mm/10 m

由于路基不均匀沉降的波长特征完全映射至钢轨表面，现仅给出64 种路基不均匀沉降组合下钢轨的位移幅值，如图4 所示，可分为3 个典型的波长范围.当沉降波长小于10 m 时，沉降幅值对轨道结构的位移映射几乎没有影响.换言之，尽管在轨道表面测得的沉降相对较小，但并不表示路基沉降也很小.该阶段的轨道脱空若能及时发现并得到注浆修复，并不会影响轨道结构的几何形态.当沉降波长发展至超过20 m 时，路基沉降量无论多大，轨道结构的位移与路基沉降一致，轨道结构与路基始终保持接触，此时恢复轨道的几何形态将非常困难.当沉降波长为16 m 且沉降波幅小于15 mm 时，轨道结构随着路基一同沉降，之后随着沉降幅值的增加，轨道结构与路基发生脱离，其位移幅值要低于真实的路基沉降幅值.

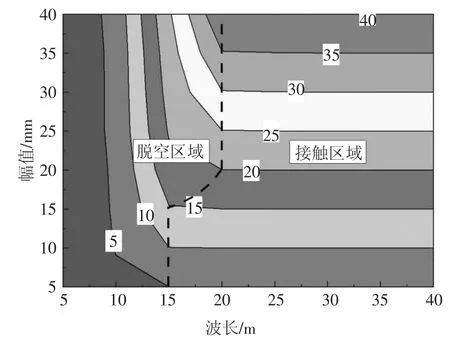
图4 路基不均匀沉降下的钢轨位移幅值Fig.4 Displacement amplitude of rail under uneven subgrade settlement

一旦路基发生不均匀沉降且混凝土底座与路基之间产生脱空后，脱空区将丧失支撑作用.从图3看，整个轨道结构作为一个整体同步产生弯曲，跨距近似等于沉降波长，则板中心最大变形可表示为：

式中：q 为施加在板表面的均布荷载；L0是跨距，即沉降波长；Dc是板的截面弯曲刚度；α 是系数；E 和h分别是弹性模量和板厚度；μ 是泊松比.对于同样的不均匀沉降跨距，轨道各层结构的变形主要由其弯曲刚度决定，根据表1 可得到钢轨、轨道板、CA 砂浆层和混凝土底座的弯曲刚度分别为：6.42×106N·m、2.40×107N·m、7.99×102N·m 和5.55×107N·m.可见，混凝土底座的弯曲刚度最大，相应的变形量最小.由于路基不均匀沉降首先映射至混凝土底座，混凝土底座的变形将决定整个轨道结构其他部分的几何形态.这也与上文描述一致，即轨道各层结构的位移保持一致.因此，可根据式（2）（3）计算得到混凝土底座变形量，即为轨道结构的整体位移量.对于给定自重荷载下的轨道结构，变形量Δmax由和Dc决定.将混凝土底座的柔度δ 定义为：

其中，q0=1 kPa，沉降波长越长，相应的柔度和变形量将越大.图5 给出了混凝土底座不同厚度和模量变化下柔度与不均匀沉降波长的关系，混凝土底座厚度和模量分别取值20～40 cm 和24～35 GPa.其中，现行高速铁路设计规范建议采用的混凝土底座厚度和模量为40 cm 和24 GPa.结果表明，混凝土底座柔度随波长呈指数式增长.当波长小于15 m 时，柔度几乎不受沉降波长甚至是厚度和模量的影响；当波长超过20 m 时，柔度快速增长，并处于较高水平；波长15～20 m 是柔度变化的过渡区.柔度随沉降波长的发展规律与图4 中的轨道位移映射规律一致，这也证实了轨道结构和路基之间的映射特性主要由混凝土底座柔度决定.若能控制路基不均匀沉降波长不超过15 m，将很大程度上降低混凝土底座柔度和轨面变形.

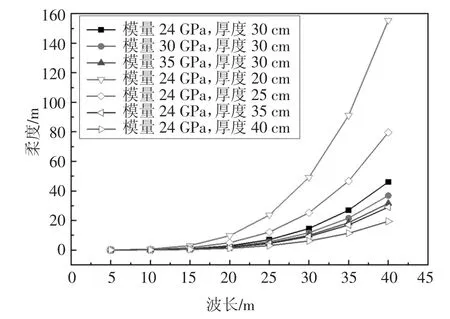
图5 混凝土底座柔度与沉降波长的关系Fig.5 Relationship between flexibility of concrete base and settlement wavelength

图6 给出了不同沉降组合下的无量纲映射关系，其中纵坐标为轨道位移映射比，定义为轨道位移幅值St与路基沉降幅值A0的比值，St/A0=1.0 表示路基沉降完全映射至轨道表面；St/A0＜1.0 表示轨道结构与路基出现脱空.横坐标是沉降幅值A0与柔度δ的比值，综合考虑沉降幅值、波长和轨道参数的影响，可以发现，轨道位移映射比与归一化的沉降幅值A0/δ 具有很好的相关关系，可通过分段函数表示：

从图6 可发现，存在临界值A0/δ=0.015，用来判断轨道结构是否与路基分离.对于A0/δ ≤0.015 的情况，位移映射比始终为1.0，对应于沉降波长大于20 m 或是波长为15 m 且幅值小于15 mm 的情况，此时路基的沉降完全映射到轨道结构，在轨道表面测得的沉降量即为路基的沉降.当归一化沉降幅度A0/δ ＞0.015 时，对应沉降波长小于15 m，此时的柔度很小，如图5 所示，位移映射比随着归一化沉降幅度的增加而迅速减小.对于沉降波长为15 m、10 m和5 m 的情况，随着沉降幅值从5 mm 增加到40 mm，轨道位移映射比分别为1.0～0.61、0.52～0.17 和0.09～0.02，这意味着此时从轨道检测获得的沉降将低于实际路基沉降量，在波长小于10 m 时尤其明显.

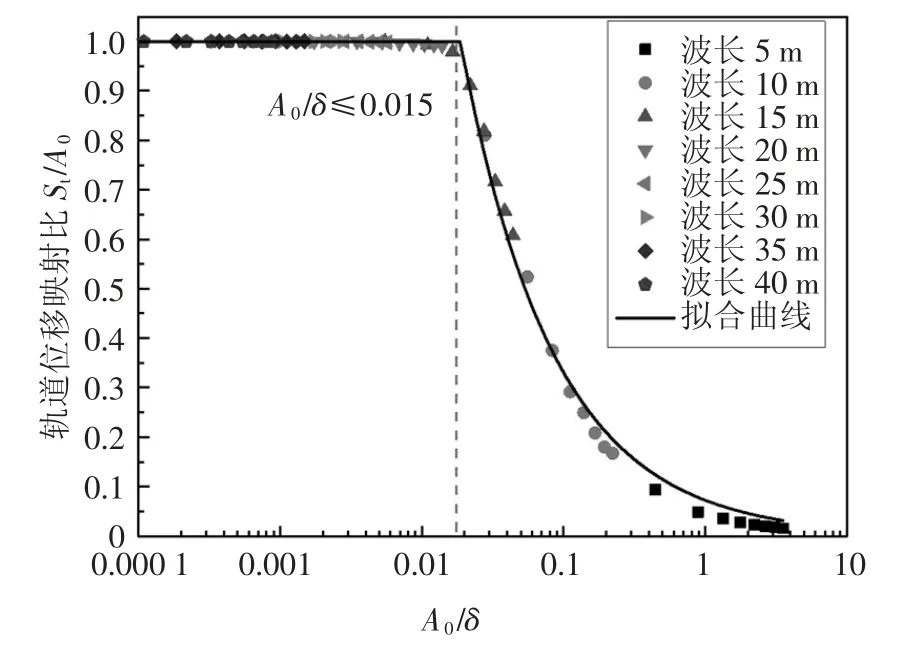
图6 无量纲位移映射特征Fig.6 Dimensionless mapping features of displacement

3 附加应力

运营初期的高速铁路路基不均匀沉降量较小，在列车行驶的间隔期，轨道结构和路基仅承受其自重荷载，轨道结构几乎不存在附加的纵向应力（温度应力除外）.一旦路基产生不均匀沉降，随着轨道变形量的增加，相应的附加应力也逐步增大，尤其是轨道结构和路基脱空后.以15 mm（波幅）/10 m（波长）为例，路基不均匀沉降引起的轨道板和混凝土底座纵向附加应力、路基接触应力分布如图7 所示.可见，轨道板和混凝土底座的底面和顶面均存在较大的拉应力区域，其中，板底的最大拉应力出现在不均匀沉降的中心区域，而板顶的最大拉应力出现在不均匀沉降引起的拱起区域.因此，在轨道结构强度设计时，轨道板和混凝土底座表面的抗弯拉能力同样值得重视.另外，路基不均匀沉降发生后，脱空区域的接触应力降为零，由于接触面积的减小，沉降区域的边缘将产生应力集中，例如沉降发生前路基表面的初始静应力为0.014 MPa，沉降发生后增大至0.5 MPa，这将加速路基土体的性能弱化.

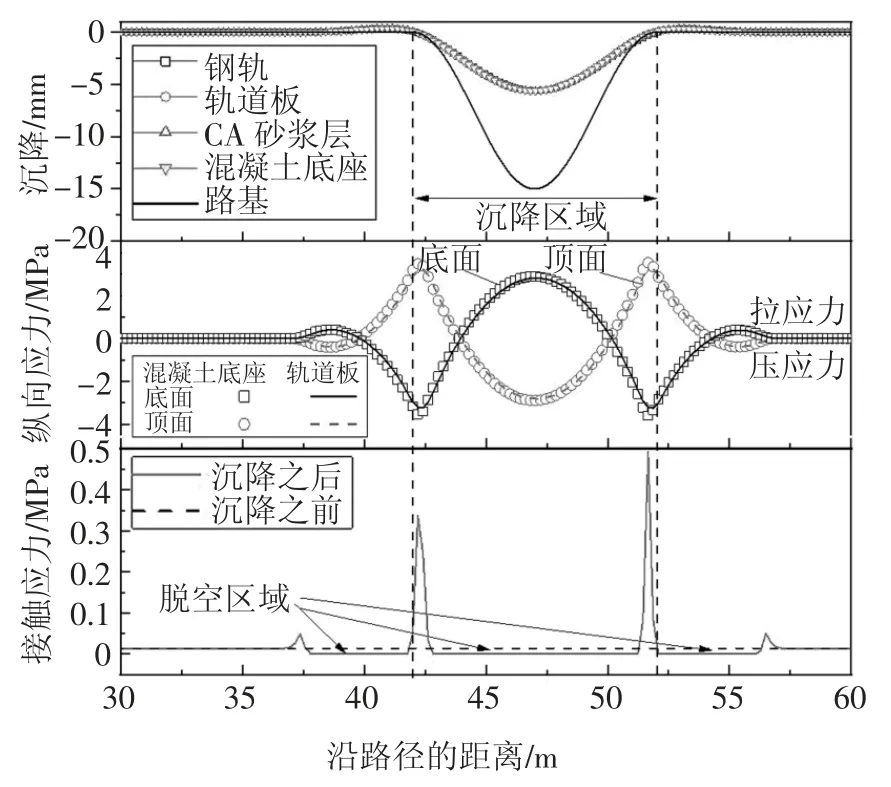
图7 15 mm/10 m 的路基不均匀沉降下附加应力Fig.7 Additional stress under uneven settlement of 15 mm/10 m

不同沉降幅值和波长组合下的混凝土底座纵向应力如图8 所示.当不均匀沉降波长低于15 m 时，混凝土底座的纵向拉应力随着波长的增加而增大.其中，沉降波长为5～10 m 时，混凝土底座的纵向拉应力基本不随沉降幅值的增加而增大，分别为0.9 MPa 和3.1 MPa；沉降波长为15 m 时，混凝土底座的纵向拉应力随沉降幅值的增加由1.6 MPa 逐渐增大至6.0 MPa；当沉降波长为20～40 m 时，混凝土底座的纵向拉应力同样随沉降幅值的增加而线性增大，随波长的增大而逐渐减小，最大值由6.9 MPa（波长20 m）减小至1.8 MPa（波长40 m）.若以C40 混凝土弯拉强度设计值5.5 MPa 为控制标准，在天窗期间仅考虑轨道结构自重作用下，不均匀沉降幅值和在对应的波长下应不超过27.5 mm（波长15 m）和31.5 mm（波长20 m）.

（2）转换层设计斜柱，安装质量控制要求高：由于建筑布置要求，周边型钢混凝土柱 2 F 楼面标高开始逐层向外倾斜，到 4 F 楼面标高恢复直立状态，外围型钢柱呈向内折线形，吊运安装质量控制要求高。

图8 不均匀沉降下的混凝土底座纵向应力Fig.8 Longitudinal stress of concrete base under uneven settlement

图9 给出了混凝土纵向应力与归一化沉降幅值A0/δ 的相关关系，其中纵坐标是纵向应力σwc与沉降波长L0的比值.对于波长大于15 m 的情况，混凝土底座与路基保持良好接触，纵向应力σwc近似表示为：

图9 纵向应力与归一化沉降幅值A0/δ 的关系Fig.9 Relationship between longitudinal stress and normalized settlement amplitude A0/δ

实际上，若考虑列车荷载的疲劳效应，不均匀沉降控制标准将更为严苛.根据混凝土疲劳强度史密斯设计理论，混凝土疲劳强度不仅取决于循环中的最大应力，而且取决于最小应力，如图10（a）所示.其中βBZ为混凝土的弯曲抗拉强度，对于C40 混凝土底座，βBZ=5.5 MPa；σwc为最小拉应力值，即自重荷载作用下的附加应力；n 为列车荷载循环次数，对于板式无砟轨道，一般考虑200 万次荷载循环，即n=2×106；σQ为疲劳强度允许值，即列车荷载引起的混凝土底座拉应力σD应低于σQ.混凝土的弯曲疲劳强度允许值σQ与附加应力σwc关系为：

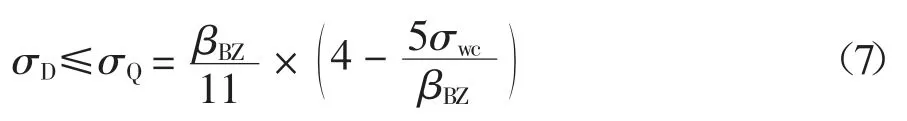
混凝土底座疲劳强度允许值与不均匀沉降幅值和波长的关系如图10（b）所示.可见，随着混凝土底座附加应力的增加，疲劳强度允许值逐渐减小.其中，当不均匀沉降波长为15 m 和20 m、相应的沉降幅值分别超过15 mm 和20 mm 时，由不均匀沉降导致的混凝土底座附加应力已达到弯曲疲劳强度允许值σQ.对于其他沉降工况，需要进一步结合列车动荷载导致的混凝土拉应力，以判断混凝土底座的疲劳开裂情况.

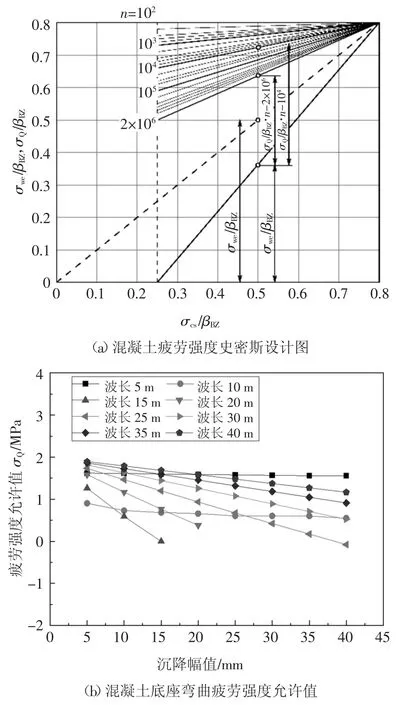
图10 混凝土底座疲劳强度Fig.10 Fatigue strength of concrete base

不同沉降组合下的路基表面接触应力峰值如图11 所示.波长为5 m 和10 m 时，接触应力稳定在0.25 MPa 和0.53 MPa.而波长为15 m 时，接触应力在沉降幅值较小时处于低应力水平，此时并未发生脱空；而后随着沉降幅值快速增加至0.65 MPa，超过了路基允许压应力0.15 MPa 的参考值[12].当沉降波长达到20 m 及以上时，路基接触应力快速减小，处于较低的应力水平.可见，路基接触应力的不利波长范围为10～15 m，且随沉降范围和幅值的增加而增大，主要集中在脱空情况下发生.列车荷载作用下，路基通常先产生波长和幅值较小的局部沉降，此时将导致接触应力重分布，使得沉降区域边缘的应力水平增加，导致土体逐渐进入屈服阶段，进而产生更大的沉降变形和更广的沉降区域.应该注意的是，在沉降波长处于10～15 m 范围内，沉降幅值和沉降范围的增长存在着恶性循环关系.因此，应及时对波长小于10 m 的局部沉降进行修复，以避免沉降区域的进一步发展和对轨道结构的潜在威胁.图12 进一步给出了路基接触应力σcs与归一化沉降幅值A0/δ 相关关系，并近似表示为：

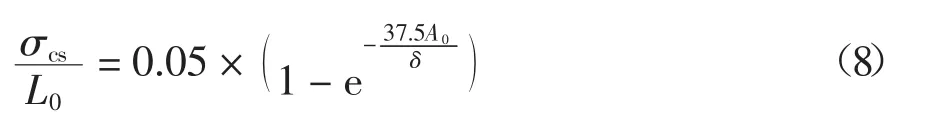
图11 不同沉降下的路基接触应力峰值Fig.11 Peak values of subgrade contact stress under different settlements

图12 接触应力与归一化沉降幅值A0/δ 的关系Fig.12 Relationship between contact stress and normalized settlement amplitude A0/δ

4 轨道结构模量与厚度的影响分析

轨道结构几何形态映射和附加应力主要与混凝土底座的柔度有关，依次选取混凝土底座模量24 GPa、30 GPa 和35 GPa，厚度20 cm、25 cm、30 cm、35 cm 和40 cm，分析其对板式无砟轨道静力学性能的影响.计算时选取路基不均匀沉降波长为20 m、幅值为15 mm.

图13 给出了混凝土底座模量对各结构层变形和受力特性的影响.轨道结构最大变形和附加应力最大值所对应的位置均处于最大沉降处上方.从图中可以看出，当模量从24 GPa 增加到35 GPa 时，路基不均匀沉降导致的轨道结构各层最大变形和混凝土底座拉应变略微减小，分别降低了约0.2%和1.9%；轨道板、CA 砂浆与混凝土底座的层间接触应力分别降低了5.3%、4.8%，而路基表面的接触应力发生了较为明显的增长，由0.17 MPa 增加至0.22 MPa，增幅24.1%，表明路基接触应力对轨道刚度的变化更为敏感.增大混凝土模量对于提高轨道结构抵抗变形能力的作用并不显著，反而增加了路基接触应力.

图13 混凝土底座模量对轨道变形和受力的影响Fig.13 Influences of concrete base modulus on track deformation and additional stress

图14 进一步给出了路基不均匀沉降作用下混凝土底座厚度变化对各结构层变形和应力的影响.从图14 可看出，当混凝土底座厚度从20 cm 增加到40 cm 时，路基不均匀沉降导致的轨道结构各层最大变形略微减小，轨道板与CA 砂浆、CA 砂浆与混凝土底座的接触应力分别降低了27.9%、29.0%；而混凝土底座拉应变和路基表面的接触应力发生了较为明显的增长，分别提高了2.9 倍和1.9 倍.可见，增大混凝土底座的厚度虽然提高了轨道的抗变形能力，但由于其自重的增加，反而导致混凝土底座拉应变和路基接触应力增幅显著.因此，在通过增大轨道结构抗弯刚度提高轨面几何平顺性时，也要考虑到其对结构自身拉应变和路基接触应力的不利影响.

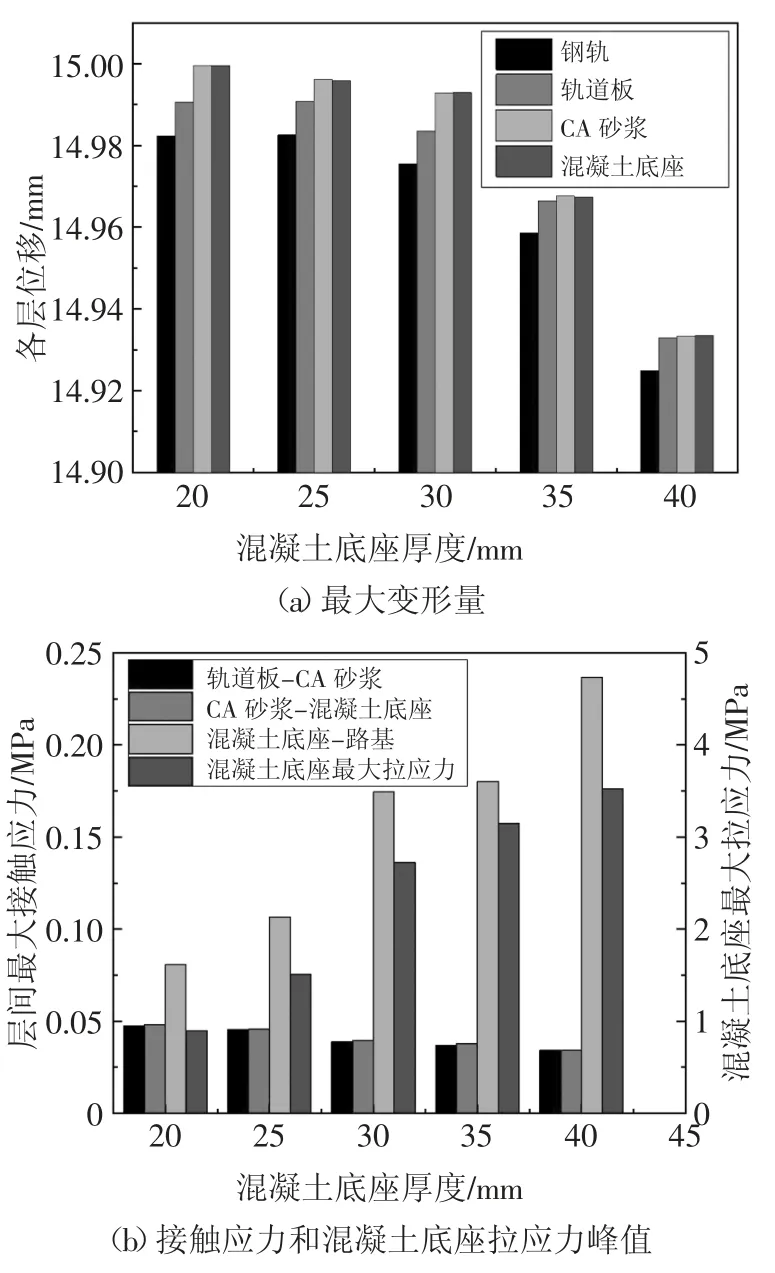
图14 混凝土底座厚度对轨道变形和受力的影响Fig.14 Influences of concrete base thickness on track deformation and additional stress

5 结论

1）轨道各层结构始终保持接触，其变形波长特征与路基不均匀沉降几乎一致，但在沉降区域的两侧出现略微的拱起；轨道结构与路基的接触状态受不均匀沉降波长和幅值的共同影响，在沉降波长小于15 m，或者波长在15～20 m 之间且沉降幅值大于15 mm 时，轨道结构与路基出现脱空，此时通过轨道结构测试得到的沉降会低估路基的实际沉降量.

2）轨道结构变形量的增加会导致混凝土结构附加拉应力和路基接触应力的增大，尤其是轨道结构和路基脱空后，附加应力也会随着沉降范围的扩大而增大.其中，混凝土底座的附加应力最接近于其疲劳强度，易发生开裂破坏；路基接触应力过大也容易导致土体产生塑性屈服，扩大不均匀沉降的幅值和范围.

3）轨道结构的映射特性主要由混凝土底座柔度决定.波长小于15 m 时，柔度很小，几乎不受沉降波长甚至是厚度和模量的影响，此时的轨道几何形态映射量很小但附加应力较高；当波长超过20 m 时，柔度快速发展，轨道变形量较大但附加应力较低；同时，轨道结构形态特征和附加应力与沉降幅值和柔度的比值A0/δ 有很好的相关关系，并分别建立了轨道结构变形量、混凝土结构附加应力以及路基接触应力与A0/δ 的经验计算公式.

4）在现有的设计参数范围内，增加混凝土底座的模量和厚度对提高轨面几何平顺性并不显著，反而会增大结构自身的拉应力和路基接触应力.

下一步将考虑引入车辆荷载，研究轨道几何形态映射对列车高速运行的影响.