考虑剪应力水平和土体干密度影响的锚-土界面剪切蠕变模型

陈昌富，温永凯，朱世民

（1.建筑安全与节能教育部重点实验室（湖南大学），湖南 长沙 410082；2.湖南大学 土木工程学院,湖南 长沙 410082）

在实际工程中，预应力锚杆都会产生不同程度的应力松弛和蠕变，其中锚固体与岩土体界面的剪切蠕变是产生这种现象的主要原因.为此，国内外部分学者通过室内外试验对锚固体-岩土体界面的剪切蠕变特性开展了研究.Kim[1]通过开展土层灌浆锚杆的拉拔蠕变试验和应力松弛试验，分析了锚杆的蠕变速率和应力损失；伍国军等[2]基于混凝土-花岗岩界面剪切蠕变试验结果，提出了一种基于经验的非线性剪切蠕变模型；陈昌富等[3-4]根据锚固单元体蠕变试验曲线，建立了具有良好拟合及预测效果的锚-土界面经验蠕变模型和分数阶导数Burgers模型.

相对于界面蠕变研究而言，国内外很多学者开展了岩土体的三轴[5-8]、直剪[9]等蠕变试验，建立了各种蠕变模型.比如，经验蠕变模型有Singh-Mitchell模型[10]、Mesri 模型[11]、卢萍珍等[6]提出的改进模型；而元件模型则有各类元件的串并联模型[12].

目前关于蠕变特性的研究，多数只利用单组蠕变试验曲线建立模型，模型中仅考虑了单个因素(即剪应力水平)对蠕变的影响.实际工程中，无论是岩土体，还是锚-土界面都是在多因素（应力水平、岩土体性质、环境条件或者注浆压力等）影响下产生剪切蠕变，而目前除考虑应力水平外还考虑其他因素影响的蠕变模型的研究相对较少.对于岩土体，有学者开展了除应力水平外还考虑含水率[13]、温度[14]及冻融循环[15]等因素影响下的蠕变模型研究.对于锚-土界面，虽然陈昌富等[16]开展了不同注浆压力下锚固体-红黏土界面剪切蠕变试验，并基于Kriging 模型建立了可同时考虑剪应力水平和注浆压力影响的锚-土界面剪切蠕变模型，但目前尚未见有同时考虑剪应力水平和土体干密度影响的锚-土界面剪切蠕变模型的研究.

此外，现有的岩土体蠕变模型或界面剪切蠕变模型基本都是根据分别加载蠕变曲线建立的，而基于蠕变等时曲线来建立蠕变模型的研究尚未见文献报道.

为探究土体干密度对锚固体-红土界面剪切蠕变特性的影响，本文开展了不同土体干密度的锚-土界面分级加载蠕变试验，利用陈宗基等[17]提出的蠕变曲线处理方法得到了分别加载蠕变曲线，并通过“等时曲线法”获得不同土体干密度的锚-土界面长期抗剪强度.利用双曲线模型对部分被选应力水平下的蠕变等时曲线进行回归分析，然后建立出双曲线模型参数与土体干密度和时间的经验关系，据此进一步建立出可同时考虑剪应力水平和干密度影响的锚-土界面剪切蠕变模型.最后，利用本文模型对参与及未参与确定建模参数的蠕变曲线进行预测，以验证模型预测精度.

1 不同干密度下锚-土界面蠕变试验

1.1 试验用料

试验所用土料为衡阳盆地红层风化残积土，取自湖南省祁东县某边坡开挖现场，其主要物理力学参数为：天然含水率w=30.7%，天然干密度ρd=1.23 g/cm3，液限wL=54.3%，塑限wp=35.3%，塑性指数Ip=19，比重ds=2.680，最大干密度ρmax=1.55 g/cm3，最优含水率wop=26.5%.试验土料不均匀系数Cu=16.67，曲率系数Cc=1.13，属于级配良好.

1.2 试验方案及装置

试样含水率w 均为26%，土体干密度ρd设置4个水平，分别为1.1 g/cm3、1.2 g/cm3、1.3 g/cm3和1.4 g/cm3，对应的饱和密度ρsat（饱和度Sr）分别为：1.69 g/cm3（0.485）、1.75 g/cm3（0.565）、1.81 g/cm3（0.656）和1.88 g/cm3（0.762）.需说明的是，每组试验均制作2个平行试样，分别用来开展瞬时拉拔试验和蠕变试验.

试样直径D 为30 cm，高度H 为10 cm，锚孔直径d为4.8 cm.试样直径与锚孔直径之比D/d=6.25>5，因此，边界效应对试验结果的影响可忽略不计[18].

实际锚固工程通常以钻孔方式形成锚孔，为模拟实际成孔方式，本文对文献[19]的制样方法进行了改进，设计制作了一套螺旋干钻法成孔的锚固单元体试样制备装置，如图1 所示.

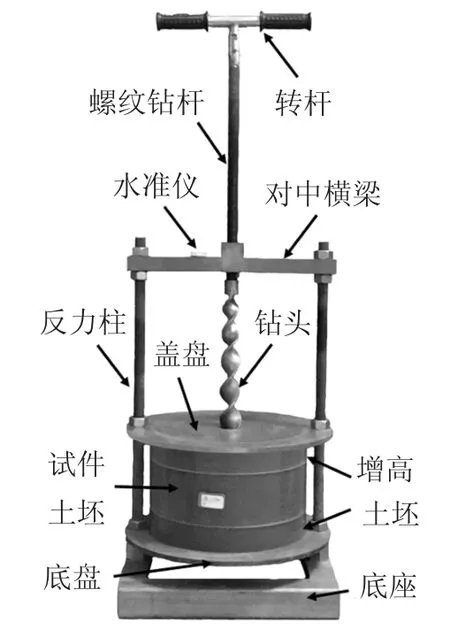
图1 钻孔装置Fig.1 Drilling device

基于滑轮组增力原理设计制作了蠕变拉拔试验装置，其增力效率为2 倍，即试样承受的拉拔力是加载砝码质量的2 倍.该装置由蠕变加载系统和数据采集系统两部分组成，具体结构如图2 所示.

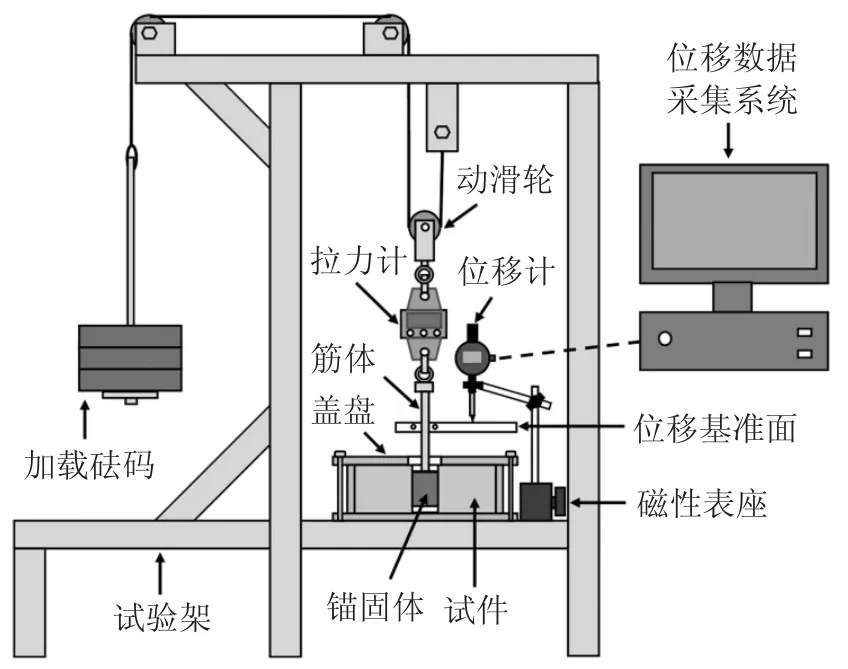
图2 锚-土界面剪切蠕变试验系统Fig.2 Device for testing anchor-soil interface creep behavior

1.3 试验方法

试验流程包括土坯制作、钻孔成孔、灌浆及试样养护以及蠕变加载等，具体如下：

1）土坯制作.利用自行研制的制样装置[19]，对含水率为26%的重塑红土料按控制干密度的方式进行分层击实，以此制备土坯.

2）钻孔成孔.首先，将土坯放置到钻孔装置的底盘中间，并利用一内径略大于锚孔直径的盖盘固定土坯；然后，转动钻杆使直径为48 mm 的钻头以10 r/min 的速率向下钻土；钻穿土坯后，回转钻杆，提出钻头，即获得以钻孔方式成孔的试样.需注意的是，为确保钻孔所成锚孔的均匀性，钻孔前，在土坯的上下面各设置高度为5 cm 的增高土坯.观察锚孔可知，孔壁呈细螺纹状，粗糙度较大.

3）灌浆及试样养护.首先，将Φ16 mm 螺纹钢筋竖直放置在锚孔中心；然后，将水泥砂浆（m水∶m灰∶m砂=0.45 ∶1 ∶1）灌入锚孔并振捣密实；水泥砂浆初凝后，将试样移至密封袋中养护28 d.

4）试样蠕变加载.蠕变试验的加载方式为分级加载.具体地，预先制作平行试样，并测定其瞬时剪切强度，再基于荷载比例（蠕变荷载与瞬时剪切强度之比）的分级方法设定蠕变加载等级为7～8 级.由于筋体-注浆体界面强度远大于锚固体-土体界面强度，因此筋体-注浆体界面不会发生剪切位移.这样，本文测定的筋体位移便为锚-土界面剪切位移，如图2 所示.此外，本试验选用的蠕变稳定标准为连续24 h 内剪切位移增量小于0.01 mm[20].

2 试验结果及分析

对试样进行蠕变加载，获得分级加载全过程曲线.利用陈宗基等[17]提出的蠕变曲线处理方法获得了分别加载蠕变曲线，得到分别加载条件下剪切位移u 与时间t 的关系曲线，如图3 所示.

图3 分别加载蠕变曲线Fig.3 Shear creep curves in different stress levels

由图3 可知，土体干密度对锚-土界面剪切蠕变特性影响显著.拉拔荷载相近时，随着干密度的增大，锚-土界面剪切蠕变位移减小，蠕变稳定时间变短.例如，剪应力近似为35 kPa 时，土体干密度从1.1 g/cm3增加至1.4 g/cm3，锚-土最终界面剪切蠕变位移u 由3.0 mm 减小至0.25 mm，蠕变稳定时间由160 h 缩减至70 h.

绘制各组试样在t 为0 h、0.5 h、1 h、2 h、5 h、10 h、20 h、40 h、60 h、80 h、100 h 和120 h 时的蠕变等时曲线，如图4 所示.将各组试样等时曲线转折点（该转折点对应的应力即为锚-土界面屈服应力，当荷载大于屈服应力后，剪切位移会显著增加，此时锚-土界面由黏弹性状态转向黏塑性状态）连线的水平渐进线在纵轴（剪应力τ 轴）上的截距作为锚-土界面长期抗剪强度τ∞.绘制土体干密度ρd与锚-土界面长期抗剪强度τ∞及瞬时抗剪强度τf关系曲线，如图5 所示.

图5 锚-土界面长期强度τ∞、瞬时强度τf 与干密度关系Fig.5 Relationship curves of anchor-soil interface long term strength and instantaneous strength versus dry density

由图4 可知：①各组试样的等时曲线均呈非线性，曲线形状类似于双曲线；②土体干密度ρd越小、时间t 越大，等时曲线非线性特征越明显.

图4 剪应力τ-剪切位移u 等时曲线Fig.4 Isochronal curves of shear stress（τ）-displacement（u）

由图5 可知，锚-土界面长期抗剪强度τ∞和瞬时抗剪强度τf均随土体干密度ρd的增加而增加，两者大致呈线性关系.因此，为简化起见，本文以线性拟合的方式建立锚-土界面剪切强度随土体干密度变化经验公式.可以看出，锚-土界面长期抗剪强度τ∞约为其瞬时抗剪强度τf的60%～80%.

3 锚-土界面双曲线剪切蠕变模型

锚-土界面剪切蠕变等时曲线实际上就是某一时刻下的剪应力-剪切位移曲线.本文试验结果表明，蠕变等时曲线的曲线形状类似于双曲线，且不同土体干密度和不同时间对应的等时曲线的曲线形态不同.因此，如果利用双曲线模型对等时曲线进行回归分析，然后建立双曲线模型参数与土体干密度和时间的经验关系，就可以进一步建立出考虑剪应力水平和干密度影响的锚-土界面剪切蠕变模型.基于该建模思路，下面以干密度ρd=1.3 g/cm3试样的衰减蠕变试验曲线为例来探讨锚-土界面衰减蠕变模型的建模方法及其合理性.

3.1 锚-土界面剪切双曲线蠕变模型

双曲线模型具有参数少、物理意义明确等优点，其方程为：

式中：τ 为锚-土界面剪应力；u 为界面剪切位移；a、b为模型参数.

定义初始剪切模量G0为锚-土界面剪应力-剪切位移等时曲线在剪应力为0 处的斜率，界面极限抗剪强度τult为等时曲线渐近线对应的极限值.由式（1）可知，模型参数a 和b 分别代表G0和τult的倒数.对于同一试样不同时刻下的等时曲线，对应有不同的G0和τult.因此，参数a 和b 与时间t 相关，假定符合一定的函数关系：

将式（2）代至式（1），可得到考虑时间效应的锚-土界面剪切双曲线模型，再对其进行变换，即可建立出锚-土界面剪切双曲线蠕变模型：

3.2 锚-土界面蠕变模型参数辨识方法

下面就采用土体干密度为1.3 g/cm3的锚-土界面衰减蠕变试验结果（图3（c）），来阐述如何确定本文提出的双曲线蠕变模型参数.

首先，利用式（1）分别对应力水平为τ1、τ3、τ4、τ6和τ7的蠕变等时曲线进行回归分析，拟合结果见图6，模型参数a 和b 如表1 所示.

图6 等时曲线拟合结果（干密度为1.3 g/cm3）Fig.6 Fitting results of isochronal curves（ρd=1.3 g/cm3）

由表1 可知，土体干密度ρd=1.3 g/cm3的试样的等时曲线拟合相关指数R2均大于0.99，这表明双曲线模型对本文蠕变等时曲线具有较好的拟合效果.此外，还可以看出，模型参数1/a 随时间t 的增加而减小，两者大致呈双曲线函数形式；模型参数b 随时间t 的变化不显著.

表1 各组干密度下等时曲线拟合结果Tab.1 Fitting results of isochronous curves for all specimens in different dry density

鉴于此，采用式（4）所示双曲线函数描述模型参数a 随时间的变化关系，而模型参数b 取均值bu.

式中：A、B、C、D 为待定参数.

采用式（4）对参数a 随时间t 变化曲线进行拟合，得到：

将式（5）代入式（3），即可得到土体干密度ρd为1.3 g/cm3的锚-土界面剪切蠕变模型：

为验证所建模型的蠕变预测效果，利用式（6）对参与建模（应力水平为τ1、τ3、τ4、τ6和τ7）及未参与建模（应力水平为τ2和τ5）的蠕变试验曲线进行预测，结果如图7 所示.

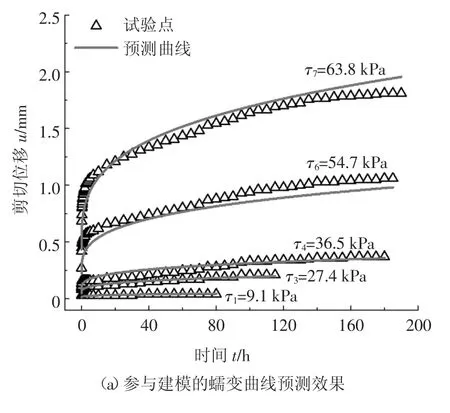
图7 蠕变曲线预测效果（干密度为1.3 g/cm3）Fig.7 Prediction results of creep curves（ρd=1.3 g/cm3）

由图7 可知，低应力水平下的蠕变曲线预测效果稍好于高应力水平下蠕变曲线预测效果.但整体而言，无论是参与还是未参与建模的蠕变曲线，本文提出的双曲线蠕变模型的预测效果均较好.

3.3 不同干密度下锚-土界面蠕变模型

采用上述建模方法，对其余3 组试样（干密度分别为1.1 g/cm3、1.2 g/cm3和1.4 g/cm3）的蠕变试验结果进行分析，并建立出相应的蠕变模型.而且，这3组试样也均选用应力水平为τ1、τ3、τ4、τ6和τ7的蠕变试验数据进行建模，其余试验数据用以模型预测.

这3 组试样的蠕变等时曲线拟合结果如表1 所示.双曲线模型参数a 随时间t 变化关系的拟合结果及模型参数b 的均值bu如表2 所示.最后，将表中参数回代至式（4）和式（3），即可得到各组干密度下锚-土界面剪切双曲线蠕变模型.

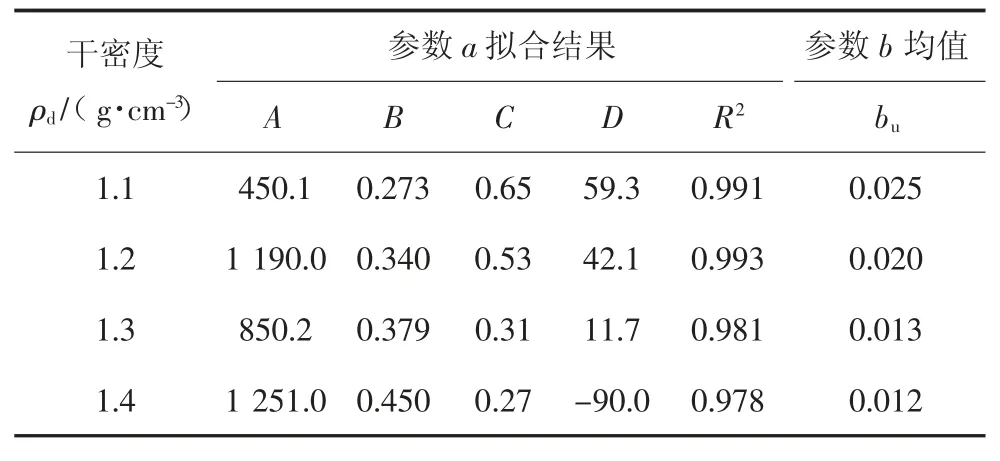
表2 模型参数拟合结果Tab.2 Fitting results of model parameters

获得其他3 组试样的锚-土界面剪切双曲线蠕变模型如下：

4 考虑剪应力水平和土体干密度影响的锚-土界面剪切蠕变方程

第3 节针对4 组不同土体干密度的试样，分别建立了仅考虑剪应力水平影响的锚-土界面剪切双曲线蠕变模型.由表2 可知，蠕变模型参数A、B、C、D 和bu均与土体干密度相关，于是通过回归分析可得到模型参数A、B、C、D 和bu与土体干密度的函数关系式，将其代入式（4）和式（3），便可得到同时考虑剪应力水平和土体干密度影响的锚-土界面剪切蠕变模型如下：

利用本文所建立的同时考虑剪应力水平和干密度影响的锚-土界面剪切蠕变模型，分别对土体干密度为1.1 g/cm3、1.2 g/cm3和1.4 g/cm3的蠕变试验曲线进行预测，获得参与建模的蠕变曲线预测效果如图8 所示，未参与建模的蠕变曲线预测效果如图9所示.

图8 参与建模的蠕变曲线预测结果Fig.8 Prediction results of creep curves which participated in modeling

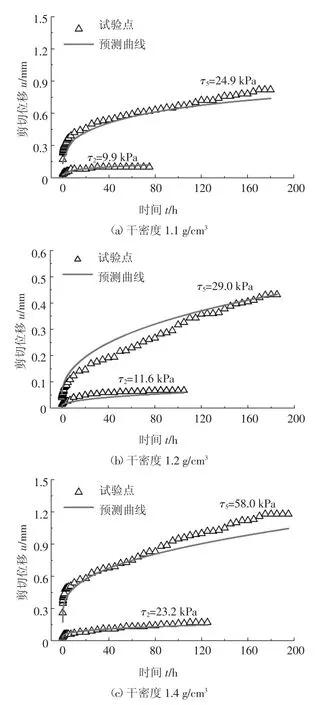
图9 未参与建模的蠕变曲线预测结果Fig.9 Prediction results of creep curves which not participated in modeling

由图8 和图9 可知，随着剪应力水平的提高，本文建立的同时考虑剪应力水平和干密度影响蠕变模型，无论是对已参与建模还是未参与建模的蠕变曲线，其预测效果均较好，这表明本文模型能够综合考虑土体干密度和剪应力水平对锚-土界面剪切蠕变特性的影响，具有较强的适用性和较高的预测精度.

5 结论

1）为探究土体干密度对锚固体-红土界面剪切蠕变特性的影响，研制了螺旋干钻成孔的锚固单元体试样制样装置以及基于滑轮组增力原理的试样蠕变加载装置，以此开展了4 组不同土体干密度的锚固单元体试样界面剪切蠕变试验，获得分级加载蠕变全过程曲线.

2）土体干密度对锚-土界面剪切蠕变特性影响显著.应力相近时，干密度越大，锚-土界面剪切蠕变位移越小，蠕变稳定的时间越短.此外，随着土体干密度的增加，锚-土界面长期抗剪强度呈线性增长，锚-土界面长期抗剪强度约为其瞬时抗剪强度的

60%～80%.

3）利用双曲线模型对部分应力水平下的蠕变等时曲线进行回归分析，然后建立双曲线模型参数与土体干密度和时间的经验关系，以此进一步建立出了同时考虑剪应力水平和干密度影响的锚-土界面剪切蠕变模型.结果表明，本文模型对参与建模还有未参与建模的蠕变曲线的预测效果均较好.