土-上盖一体化地铁车站结构耦合作用下振动台试验研究

韩学川，陶连金，张宇，史明

（城市与工程安全减灾教育部重点实验室（北京工业大学），北京 100124）

随着我国经济的快速发展，城市土地资源严重紧缺，综合利用土地和提高土地的利用效率，日益成为地铁建设重点关注的问题.地铁上盖结构加强了地铁车站与周边用地一体化规划及场站用地综合利用，提高了地铁车站的综合开发利用水平，使城市资源得到了合理利用[1].目前，我国鼓励轨道交通主体发挥自身优势，实现将地下轨道交通结构与地面结构进行联合开发的新型模式，优化城市轨道交通场站单一的建设模式，增加车站与附属地面结构的配套功能，推动土地复合利用，提高土地利用效益.据不完全统计，北京、杭州、广州等一线城市已开发轨道交通综合项目16 个，在建项目10 个，已批准建设项目50 个，在实践探索和政策创新中积累了较为丰富的经验.鉴于地铁上盖结构加强了地下地铁车站与周边用地一体化规划及场站用地的综合利用，提高了轨道交通枢纽的综合开发利用水平，使城市资源得到了合理利用，地铁上盖结构可能会成为未来轨道交通结构设计的主要趋势之一.

近年来，国内外学者针对地铁地下结构开展了多个振动台试验[2]，并取得了很多有价值的研究成果，但鉴于当时地铁地下结构的发展水平和结构形式，其研究内容多集中于单体、密贴和交叉等地铁车站结构或区间隧道的抗震性能.由于地上-地下结构体系是一个非常复杂的相互作用体系，研究内容相对较少且多限于数值模拟方面，如张天宇等[3]基于ABAQUS 软件研究了地铁车站及其上盖结构体系的地震反应特征，探讨了竖向地震动效应和转换梁刚度的影响.李延涛等[4]以地表建筑结构和地下上下平行隧道体系为背景，进行了软土场地中隧道-土-相邻上部结构体系振动台试验.刘聪等[5]通过交叉隧道振动台试验对立体交叉隧道结构地震动力响应特性及相互影响规律等问题进行了研究.王淮峰等[6]利用ANSYS 有限元程序建立了一系列典型高层框架结构及地下车站的二维平面应变模型，研究了地上结构对地下结构地震动力响应的影响参数.Pitilakis 等[7]针对地下圆形隧道地震响应规律进行了研究，分别考虑了单个和多个相邻地表结构的影响.郭靖[8]分别从场地类型和埋深等方面，研究了地表建筑对地下结构的影响范围.Robb 等[9]以动强度为主要相似参数进行了模型土的设计，研究了地震作用下地铁-结构相互作用，试验结果达到预期强度范围.Choi[10]、Huo[11]、郭靖[12]等通过地下结构与地面结构地震响应的对比总结了经验规律.

由于地铁上盖一体化结构也是近几年才大量出现且常见于地铁车辆段，地铁车站运营段上盖案例相对较少，已有的如北京地铁10 号线草桥站、北京地铁17 号线未来科技城北区公交换乘中心、通州6号线新华大街站和天津地铁6 号线北运河站等，地铁上盖结构的地震响应特性及破坏机理尚不明确，同时，建筑行业对城市轨道交通结构、地上建筑混凝土结构等均有相关规程，但缺少针对地铁上盖结构的抗震设计指导规范，这与我国地铁上盖一体化结构建设规模及前景是不相匹配的.为了深入研究地铁上盖结构的地震响应特性和破坏机理，本文以天津地铁6 号线北运河站为工程背景，开展了地铁上盖一体化结构振动台试验（YT 工况）和不考虑上盖结构的单体地铁车站结构振动台试验（DT 工况），分别从加速度和应变两方面对地铁车站结构部分进行研究，并将两种试验结果进行对比.

1 振动台试验

为研究单体地铁车站结构和上盖一体化地铁车站结构的地震响应规律，分别设计了土-单体地铁车站结构振动台试验和土-上盖一体化地铁车站结构振动台试验.本节给出了土-上盖一体化地铁车站结构振动台试验设计方案，土-单体地铁车站结构振动台试验与其相同，限于篇幅，不再赘述.

1.1 振动台测试系统与模型箱

随着振动台试验技术的提高，振动台模型试验成为研究地下结构抗震性能和破坏规律的主要手段.本试验依托北京工业大学城市与工程安全减灾教育部重点实验室模拟地震振动台系统开展.振动台的各项技术参数见表1.

表1 振动台技术参数Tab.1 The parameters of shaking table

振动台试验采用的模型箱是由课题组自主研发设计并经过优化改进后的模拟阻尼边界层状剪切模型箱，如图1 所示.层状剪切模型箱长×宽×高=2.5 m×1.4 m×1.38 m，采用矩形钢管框架竖向叠加连接，钢管架之间采用4 组直线辊针排，使模型箱更易于发生自由剪切变形运动，通过铺设特制橡胶垫有效模拟黏弹性边界吸收地震波，模型箱的有效性验证试验详见文献[13-14].

图1 振动台系统与层状剪切模型箱Fig.1 Shaking table system and layered shearing model box

1.2 振动台测试系统与模型箱

基于Buckingham π 定理开展相似关系设计[15]，从动力量纲分析入手，选择长度、弹性模量、加速度为模型结构的基本物理量，选择密度、加速度、剪切波速为模型地基的基本物理量，依次推导出其他物理量满足的相似关系，见表2.

表2 上盖地铁车站结构-模型地基体系相似关系Tab.2 Similarity relationship of model

1.3 模型结构制作

根据原型地铁车站结构尺寸和结构特点以及设计试验相似比的要求，对原型结构进行简化处理，最终确定结构模型采用抗压强度为7.1 MPa、弹性模量为6.9 GPa、泊松比为0.16 的微粒混凝土制作.根据强度相似比，试件的配筋率应保持不变.镀锌钢丝具有良好的弹性和韧性，用来模拟钢筋是合适的，模型构件中主要采用直径为Φ0.7 mm～Φ1.2 mm 的镀锌钢丝，模型结构尺寸及断面形状，如图2 所示.

图2 模型结构尺寸及断面形状（单位：mm）Fig.2 The size and cross section of structure model（unit：mm）

由于地铁上盖一体化结构模型尺寸较小，无法实现一次性浇筑完成，因此，模型结构采用分段浇筑完成.地铁上盖一体化结构模型的浇筑顺序按照地铁车站底板、车站侧墙、车站中板、车站顶板和中柱、地下室侧墙、地下室中板、地下室顶板和中柱以及上盖框架结构依次分层浇筑，模型制作流程如图3 所示.

图3 模型制作及试验Fig.3 Modeling and testing process

1.4 模型土制作

模型地基采用均一土制备，取自北京轨道交通新机场线草桥站施工的基坑中，采用分层压实法制备模型土，通过吊装漏斗将晒干、筛选后的粉细砂均匀地铺洒在模型箱内，主要控制模型土的密实度，并对模型土取样进行室内试验.模型土材料参数见表3.

表3 模型土参数Tab.3 Parameters of soil

1.5 传感器布置

上盖地铁车站振动台试验的主要监测内容包括上盖地铁车站结构模型和地基土的加速度响应规律、土-上盖地铁车站结构的动力相互作用、上盖地铁车站结构的应变响应规律以及模型地基土的侧向变形规律等.试验中采用的传感器有加速度传感器A、光纤应变片S、土压力计P、激光位移计J.鉴于结构模型尺寸较小，传感器布置数量较多，为了能够满足试验需要分别选取主观测面、辅助观测面和次观测面.振动台试验中模型地基和结构中传感器布置，如图4、图5 所示.

图4 上盖地铁车站工况模型地基传感器布置图Fig.4 The layout of soil sensors in upper subway station model

图5 上盖地铁车站传感器布置Fig.5 The layout of sensors in upper subway station model

1.6 地震波选择及加载工况

考虑近远场地震动对上盖地铁车站结构的影响，选取八角什邡波、名山波和凤翔波3 种具有不同震中距的地震波进行研究.其中八角什邡波属于近场地震动，名山波属于中场地震动，凤翔波属于远场地震动.3 条地震波加速度时程曲线及其相应的傅里叶谱如图6 所示.

图6 输入地震波时程曲线及傅氏谱Fig.6 Time history curve and Fourier spectrum of input seismic wave

振动台试验时，截取地震波较为强烈的前80 s作为输入地震波，每次峰值加速度改变时均进行一次白噪声扫描，以确定模型体系的自振特性的变化.采取阶梯逐级加载的方式加载，将输入地震波峰值加速度分别调整为0.1g、0.3g、0.5g、0.7g 和1.0g，地震波激振前后输入0.1g 的白噪声，量测模型自振频率等动力特性的变化.根据1.2 节相似比设计，除白噪声外，输入地震波持续时间按1/2 进行压缩.振动台试验地震波加载工况见表4.

表4 上盖地铁车站结构振动台试验地震波加载工况Tab.4 The case of shaking table test

2 上盖一体化地铁车站振动台试验结果分析

限于篇幅，本节分别从加速度和应变两方面对上盖一体化地铁车站结构部分进行研究，并将试验结果与单体车站结构进行对比分析.

2.1 模型土体加速度反应分析

上盖一体化地铁车站结构振动台试验中，通过监测不同深度处的加速度变化规律，分析加速度在模型土中的传播规律.在上盖一体化地铁车站结构一侧模型土体内部沿埋深自上而下布置加速度传感器JA7、JA8、JA9、JA10 和JA11，在模型土箱底部布置加速度传感器JA16，将其监测结果作为振动台实际输入加速度结果.为了比较不同地震工况下，上盖一体化地铁车站结构工况中模型土体的加速度变化情况，图7 给出了模型土体内部监测点的加速度峰值及加速度放大系数变化曲线.定义各监测点加速度峰值与振动台面监测点JA16 加速度峰值的比值为该监测点的加速度放大系数.其中，凤翔波存在脉冲加速度，导致振动台会出现较大的瞬时位移，限于振动台最大位移，凤翔波最大加速度仅能加到0.3g.

图7 模型土各监测点加速度峰值及放大系数Fig.7 Peaking acceleration and acceleration amplification factor of points of model soil

可以看出，模型土体相同监测点的加速度峰值随输入地震强度的增加逐渐增大，而加速度放大系数则逐渐减小.不同地震工况下，受地震波自身特性的影响，模型土监测点的加速度峰值和放大系数沿埋深的减小表现出的规律有所差异，其中，当输入地震强度较小（0.1g、0.3g）时，模型土体内部监测点的加速度峰值及加速度放大系数沿埋深的减小逐渐增大，加速度放大系数基本都大于1；当输入地震强度较大（0.3g 以上）时，名山波作用下模型土体内部监测点的加速度峰值及放大系数呈先减小后增大的趋势，而什邡波则呈“S”型变化趋势，即表现为先增大再减小然后增大的趋势，加速度放大系数小于1 的监测点逐渐增多.这表明，当输入地震强度较小时，模型土体处于弹性工作状态，地震波由底部向上传播过程中具有显著的放大作用；而随着输入地震强度的逐级增加，模型土体由弹性工作状态进入弹塑性工作状态，模型土体更加密实，土-结构动力相互作用明显，模型结构出现损伤，导致刚度弱化，而靠近模型结构监测点A8 和A9 的非线性现象愈加凸出.

图8 给出了0.7g 八角什邡波作用下，监测点JA7～JA11 以及JA16 的加速度时程曲线和傅里叶谱图.YT-SF-7-JAX 表示输入0.7g 的八角什邡波时上盖一体化地铁车站振动台试验测点X 的加速度.

图8 输入0.7g 什邡波工况下测点加速度时程及傅里叶频谱图Fig.8 Acceleration time histories and Fourier spectrums of measured points under 0.7g Shifang wave input

由图8 可见，加速度方面：0.7g 什邡波工况下模型土监测点JA7、JA8、JA9、JA10 和JA11 加速度峰值出现时刻分别为10.41 s、10.82 s、10.82 s、10.81 s 和10.80 s，加速度峰值分别为0.91g、0.72g、0.59g、0.62g和0.60g.频谱方面：模型土监测点JA7、JA8、JA9、JA10 和JA11 的主频率分别为7.43 Hz、7.41 Hz、7.47 Hz、7.41 Hz 和7.38 Hz，模型土监测点的主频率呈向7～12 Hz 范围转移的趋势.模型土体监测点JA7、JA8、JA9、JA10、JA11 和JA16 的傅里叶频谱图明显不同，说明地震波由模型土体底部输入到达顶部的传播过程中，输入地震波的频率特性发生了显著改变.模型土体底部监测点JA10、JA11 的频谱组成与JA16 基本相同，频谱分布相对均匀，而上部监测点JA7、JA8、JA9 的频谱组成则表现为高频向低频转移，高频成分逐渐滤波的趋势.同时，随着输入地震强度的逐级增加，模型土体的自振频率逐渐减小，与模型土体自身频率接近的频率段放大效应显著.

图9 给出了2 种试验工况下模型土体监测点JA1、JA2、JA3 的加速度时程曲线和傅里叶谱图，DTSF-3-JAX 表示输入0.3g 的八角什邡波时单体地铁车站振动台试验中测点X 的加速度时程.其中，JA1位于模型结构正上方接近地表位置，JA2 和JA3 分别位于模型结构正下方，与监测点JA1 处于同一竖向位置，通过对比DT 工况和YT 工况下监测点JA1、JA2、JA3 的加速度时程曲线和傅里叶谱分布规律，可以更好地说明不同试验工况下模型结构对地震波传播过程影响的差异.

从图9 中可看出，不同地震强度时，DT 工况与YT 工况车站结构相同监测点的加速度时程曲线和傅氏谱曲线基本相同，加速度峰值均出现在同一时刻；相同监测点的卓越频率基本一致，主频范围均表现为高频向低频转移的趋势.DT 工况与YT 工况监测点加速度峰值均表现为随输入地震强度的增加逐渐增大，YT 工况加速度峰值小于DT 工况.监测点JA1、JA2、JA3 在DT 工况下的加速度峰值和放大系数 分别为0.33g、0.20g、0.21g 和1.67、1.01、1.04；在YT 工况下的加速度峰值和放大系数分别为0.31g、0.17g、0.19g 和1.38、0.76、0.87.可看出，YT 工况小于DT 工况，随埋深的增加，加速度放大效应差异逐渐增大，这是因为2 种工况下模型土主频率虽然相同但DT 工况下地震波位于主频范围内的能量分布相对集中，导致加速度放大效应更加明显，这一点可从JA1 加速度频谱图中看出.

图9 模型土体各测点加速度峰值及傅里叶谱幅值Fig.9 Peak acceleration and Fourier spectrum of model soil

2.2 模型结构加速度反应分析

图10 给出了不同地震工况不同地震强度作用下，模型地铁车站中柱各监测点的加速度峰值及加速度放大系数变化曲线.定义监测点加速度峰值与振动台面监测点JA16 加速度的比值为该监测点的加速度放大系数.

图10 结构中柱各测点加速度峰值及放大系数Fig.10 Peaking acceleration and acceleration amplification factor of middle column

可以看出，模型车站中柱监测点的加速度峰值随输入地震强度的增加逐渐增大，中柱顶部监测点JA20 的加速度峰值最大，底部测点JA22 的加速度峰值最小.各地震波工况下中柱的加速度放大系数则表现为随输入地震强度的增加呈逐渐减小的趋势，这主要是因为地震强度逐渐增大时，模型结构由弹性工作阶段逐渐进入弹塑性阶段，中柱的损伤更加严重，伴随着刚度退化的现象.当输入地震波强度较小时，中柱监测点的加速度峰值和加速度放大系数相差较大，反之较小.

图11 给出了不同强度名山波工况下2 种车站结构中柱顶部监测点JA20 的加速度时程曲线和傅里叶谱图，参数对比见图12.可以看出，不同地震强度时，DT 工况与YT 工况车站结构相同监测点的加速度时程曲线形式基本相同，加速度峰值均出现在同一时刻.地震波加速度峰值相比，DT 工况与YT 工况均表现为随输入地震强度的增加逐渐增大，YT 工况加速度峰值小于DT 工况，其中，0.3g、0.5g、0.7g 地震强度下的加速度峰值幅值变化率分别为5.12%、2.32%、2.11%，说明随着地震强度的增加，2 种工况加速度峰值的差异呈逐渐减小的趋势；频率相比，DT工况与YT 工况的卓越频率基本相同，表现为随输入地震强度的增加逐渐减小，主频范围呈高频向低频转移的趋势；傅氏谱幅值相比，DT 工况与YT 工况的傅氏谱幅值均表现为随输入地震强度的增加逐渐增大，YT 工况卓越频率对应的幅值小于DT 工况，说明DT 工况下卓越频率附近的地震能量相对集中.

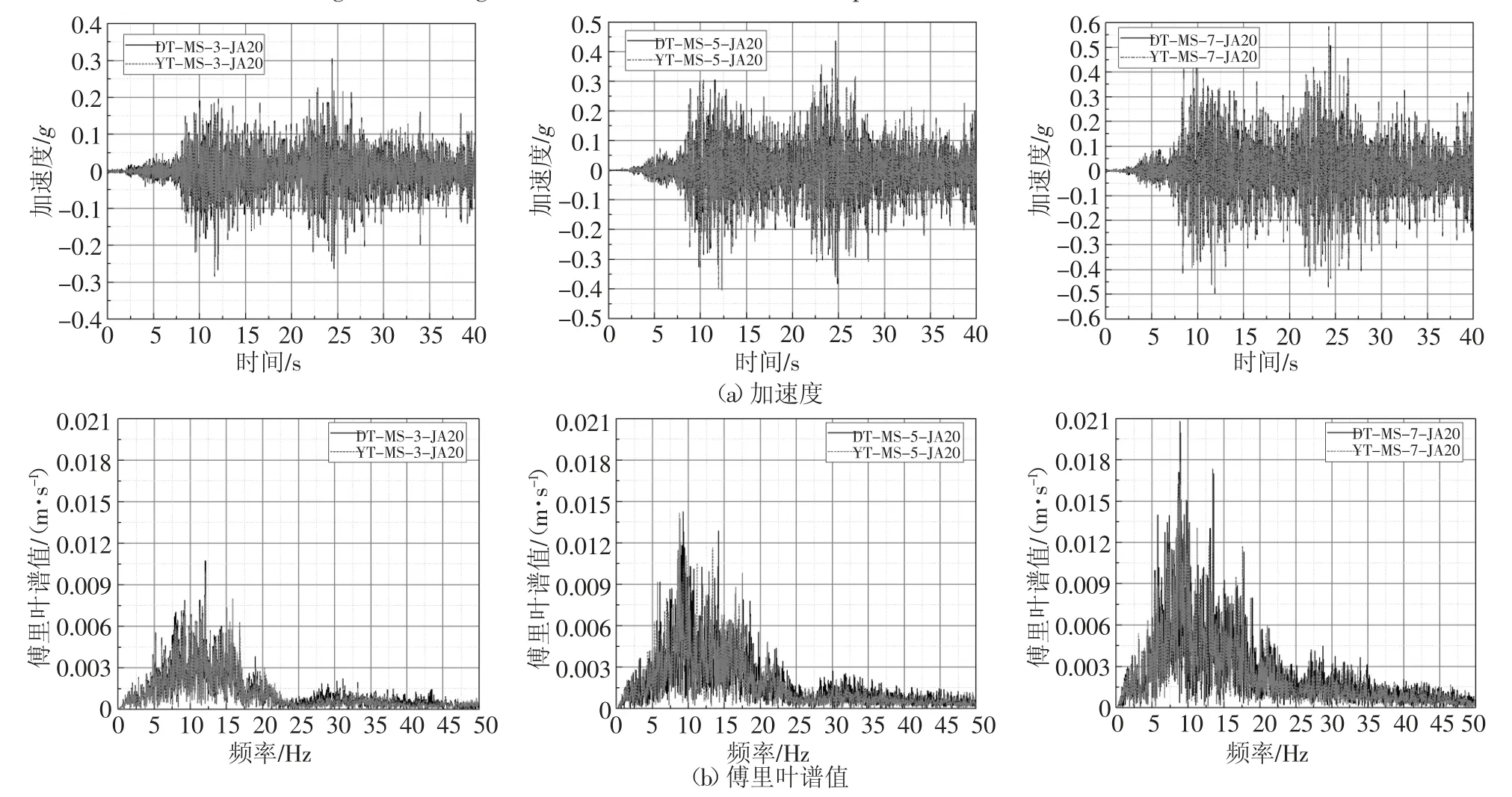
图11 结构中柱各测点加速度时程曲线及傅里叶谱值Fig.11 Time histories and Fourier spectra of middle column

图12 不同试验工况参数对比图Fig.12 Comparison of parameters of different test conditions

2.3 模型结构应变反应分析

考虑到量测设备数据采集通道数量有限和最大限度地满足试验需要，近似认为模型结构呈左右对称的地震响应规律，选取地铁车站左半区域为研究对象，开展结构应变反应规律研究.以往研究成果表明，混凝土结构主要发生受拉损伤，受压损伤程度较小，因此，本节主要针对模型结构的拉应变地震反应进行分析.图13 给出了不同地震动作用下模型结构主观测面的拉应变幅值分布图.

图13 不同地震动作用下主观测面拉应变幅值（单位：με）Fig.13 Stretching strain amplitude of subway structure under different ground motions（unit：με）

可以看出，模型结构各测点的应变峰值表现为八角什邡波（近场波）＞名山波（中场波）＞凤翔波（远场波）.其中，相同地震波作用下，随着地震强度的增加，模型结构的拉应变幅值呈逐渐增大的趋势，模型中柱端部的拉应变幅值最大，侧墙次之，楼板最小，这是因为中柱横截面积较小且没有周围土体提供抗力，导致承载力相对不足，水平地震作用下更容易发生破坏，说明中柱仍然是上盖一体化地铁车站结构抗震设计的薄弱部位.侧墙和中柱顶底部监测点应变幅值明显大于中部位置，这是因为地震作用下模型结构和土体同步运动，导致结构发生剪切变形，中部位置邻近反弯点且随地震强度的增加反弯点逐渐向上偏移.

DT 试验工况和YT 试验工况中，不同地震强度下地铁车站侧墙和中柱各监测点的拉应变幅值，见表5.与DT 试验工况相比，YT 试验工况下模型结构监测点的应变相对较小，什邡波作用下的应变幅值差异大于名山波，应变幅值均表现为随着输入地震强度的增加逐渐增大.YT 工况与DT 工况相比，输入0.1g 地震波时，应变率为1.5%～3.7%；输入0.3g 地震波时，应变率为4.1%～6.0%；输入0.5g 地震波时，应变率为6.1%～7.7%，说明随着地震强度的增加，应变变化率逐渐增大，但变化率增幅逐渐减小.

表5 不同工况下结构各测点应变幅值Tab.5 Strain amplitude of points in different conditions

图14 和图15 分别给出了名山波作用下，YT 工况和DT 工况中柱监测点S5 的应变时程曲线.表6给出了2 种试验工况车站中柱监测点S5 的残余应变幅值.可以看出：不同地震强度作用下，监测点的应变时程曲线与输入地震波波形有所差异.当输入地震强度较小（0.1g 和0.3g）时，监测点具有很小的残余变形，输出应变时程曲线与输入地震波时程曲线变化规律相似；当输入地震强度较大（0.5g 和0.7g）时，监测点具有明显的残余变形，残余应变幅值随着地震强度的增加逐渐增大，输出的应变时程曲线与输入地震波时程曲线变化规律出现明显差异.由表6 可看出：与DT 工况相比，YT 工况地铁车站结构的残余应变幅值相对较小，残余应变变化率随着地震强度的增加逐渐增大，说明地震强度越大，2 种地铁车站结构的残余应变差异越大.

图14 YT 工况下中柱顶底部应变时程曲线Fig.14 Strain time histories curve of top and bottom of structure column under YT condition

图15 DT 工况下中柱顶底部应变时程曲线Fig.15 Strain time histories curve of top and bottom of structure column under DT condition

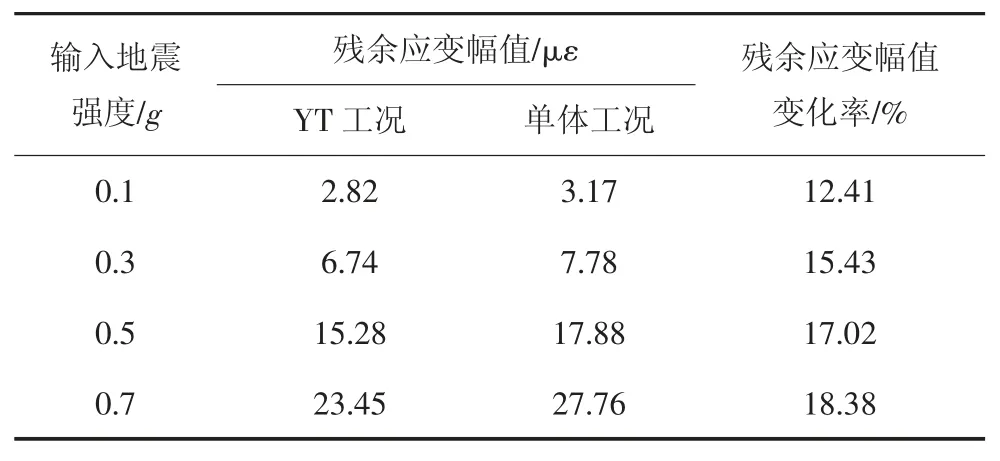
表6 结构监测点S5 残余应变幅值Tab.6 Residual strain amplitude of structural measuring point S5

3 结论

本文以上盖一体化地铁车站结构为研究对象，开展了粉细砂场地上盖地铁车站结构和单体地铁车站结构动力反应规律分析，分别从加速度和应变两方面对地铁车站结构部分进行研究，并将两2 种试验结果进行对比，基于本文分析可得出如下结论：

1）相同地震波作用下，上盖地铁车站模型土和车站结构的加速度峰值及加速度放大系数小于单体地铁车站，近场地震动下加速度放大系数差异较大，远场地震动下加速度放大系数差异较小，埋深越深差异越明显，但加速度峰值及加速度放大系数变化规律基本一致，说明结构形式的不同对场地加速度的变化规律影响较小.

2）上盖一体化地铁车站相同监测点加速度峰值大致表现为八角什邡波（近场）＞名山波（中场）＞凤翔波（远场），不同地震波之间加速度峰值差异较大，但加速度峰值差异随地震强度增加逐渐减小.

3）上盖一体化地铁车站各测点的应变峰值表现为八角什邡波（近场）＞名山波（中场）＞凤翔波（远场），应变峰值变化规律与DT 工况大致相同，均表现为随着输入地震强度的增加逐渐增大.与DT 试验工况相比，YT 试验工况下模型结构监测点的应变峰值相对较小，近场地震动作用下的应变峰值变化率大于远场地震动，随着地震强度的增加，应变峰值变化率逐渐增大，而变化率增幅呈逐渐减小的趋势.