利用关联性资源促进学生深度学习

吴鹏飞

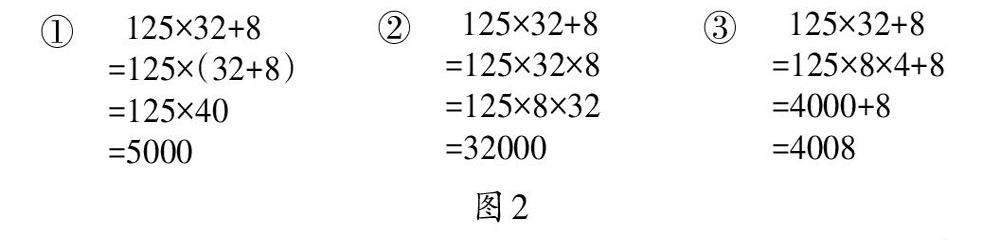
[摘 要]关联性资源是个体利用已有认知结构与新知进行关联时的思维路径和方法，它是促进学生深度学习的有效途径之一。通过比较相似资源，凸显核心算理;利用错误资源，引发认知冲突;挖掘内隐资源，引发深度思考三个方面入手，能促进学生深度学习真正发生。

[关键词]关联性资源;深度学习

学生学习新知前，头脑里并非是一张白纸，而是已经存在着相关的旧知。由于不同学生的已有认知结构和思维方式存在着差异，导致他们进行新旧知关联的方式、方法不同，合理利用这些差异是实现“人人都能获得良好的数学教育，不同的人在数学上得到不同的发展”目标的有效路径之一。为了便于表述，笔者把个体利用已有认知结构与新知进行关联时外显的思维路径和方法称为关联性资源。学生在建构新认知结构时，关联性资源起着连接和支撑的作用，而深度学习强调学生积极主动地将新旧知进行关联，因此，合理利用不同的关联性资源不仅是落实以学生发展为本的实践途径，还是实现深度学习的有效途径。下面，笔者以人教版四年级计算教学为例谈几点探索性的思考。

一、比较相似资源，凸显核心算理

单凭个人的经验去探索新的认知结构，其过程极其不稳定，这种单线关联的效果极其低下甚至无效，只有在比较和借鉴其他个体的关联性资源中，才能形成纵横交错、稳定结实的网状认知结构。

“三位数乘两位数”是“两位数乘两位数”的延续和拓展，学生对“两位数乘两位数”算理的理解程度及遗忘程度直接决定着“三位数乘两位数”的教学策略。

在教学“三位数乘两位数”时，为了让学生对新旧知进行充分关联，笔者先让学生试着用两位数乘两位数的方法算一算，并把详细的思考过程写下来。之后，笔者收集并分析各种资源产生的原因，进而读懂学生的认知起点和思维的差异。表1是笔者所教班级学生的关联性资源统计表。

从统计表上可得出，81%的学生都能根据已有经验算出正确答案;60%的学生能利用转化思想和乘法分配律用横式计算;35%的学生能用竖式计算，但说不出算理，只会机械模仿;5%的学生能依据转化思想、乘法分配律和十进制计数法列竖式计算。结合以上关联性资源的分析不难发现，掌握竖式计算并理解十进制计数法在竖式中的应用是本节课的重点。

有不同才能触发比较，有比较才能引发深度思考。笔者展示方法1～方法5，让学生试着读懂这些算式，并找出它们的相同点与不同点。

生1：相同点有三个，分别是1.结果相同;2.都是横式;3.都把其中的一个乘数分解成几个数相加的形式。

生2：不同点是其中的一个乘数分解的方法不同。

师（追问）：从这五种方法中选择你喜欢的一种，并试着用一个竖式表示145×12的计算过程。

选择方法1、2、5的学生在列竖式时遇到障碍，究其原因，是这些方法不满足十进制计数法。方法3、4满足十进制计数法，所以选择这两种方法的学生佷容易就列出竖式（如图1）。

在比较上面四个竖式后，学生发现1450的个位上的0省略不写是正确且简洁的。竖式④虽然从本质上讲也是正确的，但是比较繁杂。

总之，在比较关联性资源的过程中，学生在原有认知的基础上明晰了十进制计数法是笔算乘法的核心算理，明白了竖式只是核心算理外显的表现形式。这一过程中，学生的运算能力和推理能力均得到了提升，深度学习得以实现。

二、利用错误资源，引发认知冲突

当学生对新知的理解片面、不深刻时，用新知解决问题的过程中就会产生思维混乱。教师要善于利用这种资源制造矛盾冲突，让学生产生纠正错误的内驱力，让学生在疑惑、探索、释疑中真正明白自己所困惑的问题。

乘法结合律和乘法分配律形式相似但本质不同，在学习初期，很多学生对这两个定律没有一个完整且清晰的认识，就容易在具体运用时混淆，导致运算错误。根据这种情况，笔者设计了一道简便计算题：125×32+8。学生独立完成后，笔者收集到以下资源（如图2）。

分析算式，笔者发现学生只是根据数的特点随意凑整进行運算，根本没有真正理解这两条定律的本质。为了加深学生对这两条定律的理解，详细分析出错原因是关键，于是笔者展示图2的三种算法，并提问：“这三个算式的结果都不同，你认为哪个对，哪个不对？并说出理由。”学生经过观察比较、倾听交流、分辨异同、明理辨析后，发现共同利用乘法分配律和乘法结合律是解决简便计算题的有效途径。

引发认知冲突，激发学生探究知识和挖掘本源的欲望，引导学生往数学本质的纵深处探索，可使学生的认知结构不断扩充和发展。

三、挖掘内隐资源，引发深度思考

隐性资源只有受到特定的刺激才能被激活，并经过反思、顿悟才能使资源显现。这一特定的刺激要求教师不仅营造民主、平等、和谐的课堂学习氛围，还应利用核心问题激发内隐资源，引发学生深度思考。

在教学“小数的加法和减法”之前，学生已经学习了小数的意义、小数的读写和小数的性质等知识。本单元中的例2比例1更能凸显个体已有认知结构和新知的冲突，更有利于学生理解算理。鉴于此，笔者把例1（6.45+4.29和6.45-4.29）作为学习例2的前测题，并选择数学成绩在我校处于中等水平的班级进行前测，全班正确率达100%，检测结果在预设范围内。

上课时，笔者直接出示例2（6.45+8.3），让学生独立计算。笔者课前预测了7种关联资源（如图3）。

从课堂上收集的资源看，全班有60位学生列的是竖式⑦，有1位学生列的是[6 .  4  58 .  3  0] [+][14 . 7  5] 。这种情况完全颠覆了课前预设，学生并没有出现上述的其他关联资源，于是笔者立即放弃通过比较不同算式激化思维冲突的做法，试着从学生对算理的理解上突破。通过询问，学生有的认为是小数点对齐，有的认为是相同数位对齐。史宁中教授指出：“为了理解小数，其核心在于重新理解十进制。”显然，十进制计数法是小学阶段小数的核心知识，要想检测学生是否真正理解十进制，笔者只能从学生对这两句话的深刻理解上再次寻找突破口：“在小数点对齐和相同数位对齐这两句话中，你只能选一句作为你计算的理由，你选那一句？”这个问题把对十进制理解处于模糊状态的学生暴露出来。有学生选择小数点对齐，理由是如果小数点对齐了，相同数位就一定会对齐，如：[8 .  3  54 .  5] [+]  。就这样，内隐资源挖出来了，思辨的对象也明确了，学生就很容易理解小数点对齐的本质是相同数位对齐。

正如美国教育家杜威所说：“真正的思维必然是以认识到新的价值而告终。”教师只有把学生思维中含糊的、可疑的、失调的内隐资源挖掘出来，引发深度思考，思辨交锋，才能促使学生对知识有新的认识，实现深度学习。

总之，关联性资源取之于学生，用之于学生。聚焦关联性资源，满足不同学生以熟悉的、关联的方式去学习，促进深度学习真正发生。

（责编 李琪琦）