基于广义欧拉商二元序列线性复杂度研究
2021-09-30姚晓艳李富林
姚晓艳, 李富林
(合肥工业大学 数学学院,安徽 合肥 230601)
序列密码也称流密码,具有实现简单、便于硬件实施、加解密处理速度快、没有或只有有限的错误传播等特点;在保密通信中,是一类非常重要的密码体制。序列密码系统的稳定性对系统的安全有很大的影响,虽然如何设计稳定性好的流密码系统没有一个明确的标准,它取决于流密码模型,但是在任何情况下都应该保证密钥流序列的稳定性。密钥流序列的稳定性很大程度上反应了密钥流序列的安全性。线性复杂度和错误复杂度是度量密钥流序列稳定的重要指标,具有足够高的线性复杂度必须作为安全密钥流序列的必要条件[1]。由B-M算法知,连续2L(L为序列的线性复杂度)个连续比特就可以恢复整个序列,因此,密钥流序列的的线性复杂度必须足够大且至少大于周期的1/2,才能抵抗敌方的截获和破译。
费马商是一个古老的数论问题,它在密码学研究领域有着重要的应用,文献[2]讨论了费马商序列的线性复杂度等密码学性质;文献[3-4]应用费马商的乘法特征,进一步讨论了伪随机序列和布尔函数的相关特征。这些研究结果充分表明,费马商在设计密码本原中有着积极的意义。欧拉商实际上是费马商的进一步推广,文献[5-8]进一步研究了来自欧拉商二元序列的线性复杂度性质。
本文推广了欧拉商的一些性质,并应用这些性质构造的二元序列具有良好的线性复杂度性质,在p(奇素数)模4的情形下,序列的线性复杂度大于周期的1/2,尤其是在p(奇素数)模4余3的情形下,线性复杂度仅仅比周期少1。
1 基础知识
根据欧拉定理,若p为奇素数,r为整数,对所有整数u有gcd(u,p)=1,则uφ(pr)≡1(modpr)。
定义欧拉商为:
0≤Qr(u) 若整数uφ(pr)=1+a1pr+a2P2r+…∈Z,0≤ai 当gcd(u,p)>1时,假设Qr(u)=0。 若u、v为整数且gcd(u,v)=1,则 Qr(uv)≡Qr(u)+Qr(v)(modpr), Qr(u+kpr)≡Qr(u)-kpr-1u-1(modpr)。 欧拉商在数论和密码领域中有着重要的应用,利用欧拉商构造的伪随机序列在序列密码和扩频通信等领域中有着极为广泛的应用。线性复杂度是衡量序列密码安全性重要指标之一,从密码学角度研究欧拉商及其扩展函数的应用是新兴的研究热点。本文首先定义广义欧拉商,并讨论广义欧拉商的性质,在此基础上,构造了一类线性复杂度大的二元序列。 在欧拉商定义中,应用到uφ(pr)≡1(modpr),其中,gcd(u,p)=1。 事实上,总存在最小的正整数χ,使得uχ≡1(modpr)且χ|φ(pr)。 定义χ为u(modpr)的乘法阶, 其中,gcd(u,p)=1。 当gcd(u,p)>1时,设Hr(u)=0。称Hr(u)为广义欧拉商。若整数uχ=1+a1pr+a2p2r+…, 0≤aj 性质1 当gcd(u,p)=1时,有 Hr(u+kpr)≡Hr(u)+kχu-1(modpr)。 证明设u(modpr)的阶为χ,则u+kpr(modp)的阶也是χ,因此 Hr(u)+kχu-1(modpr)。 性质2 欧拉商和广义欧拉商有如下关系: 证明显然,当gcd(u,p)>1时,Qr(u)和Hr(u)均为0。当gcd(u,p)=1时,设整数 uχ=1+a1pr+a2p2r+…, 0≤aj 即Hr(u)=a1,则 uφ(pr)=(uχ)φ(pr)/χ= (1+a1pr+a2p2r+…)φ(pr)/χ= 于是 证明显然,当gcd(u,p)>1时,Hr(u)和Hr(uk)均为0。 下证当gcd(u,p)=1时的情形。设整数 uχ=1+a1pr+a2p2r+…, 0≤aj 若gcd(χ,k)=d,则uk(modpr)的乘法阶为χ/d。于是 性质4 任意与p互素的整数u、v,若它们的乘法阶分别为χu、χv且满足gcd(u,v)=1,则有Hr(uv)≡χvHr(u)+χuHr(v)(modpr)。 证明uv的乘法阶为χuv=χuχv,即(uv)χuv=(uv)χuχv≡1(modpr),则 Hr(uv)≡ Hr(uχv)+Hr(vχu)(modpr)。 再由性质3、性质4得证。 定义序列(e(u))u≥0∶设u≥0, (1) 由性质1知,Hr(u)在(modpr)条件下是一个最小周期为p2r的序列,因此(eu)u≥0的周期也为p2r的序列。下面考虑(eu)u≥0的线性复杂度。 设F为一个域。对于F上周期为T的序列(s(u))u≥0,(s(u))u≥0的线性复杂度记作: s(u+L)=cL-1s(u+L-1)+…+ c1s(u+1)+c0s(u),u≥0, 其中:c0≠0;c1,…,cL-1∈F。设 S(X)=s(0)+s(1)X+s(2)X2+…+ s(T-1)XT-1∈F[X] 为(s(u))u≥0的生成多项式,则F上(s(u))u≥0的线性复杂度为: LCF(s(u))u≥0=T-deg(gcd(XT-1,S(X)))。 另外,设2是模p2的本原元,即2关于模p2的乘法阶为φ(p2)。 定理1设(eu)是F2上周期为p2r、形如(1)式的序列。若2是模p2的本原元,则(eu)的线性复杂度满足: 对应的极小多项式满足: 证明因为2是模p2的本原元,所以在F2上多项式xp2r-1可因式分解为2r+1个即可约多项式的乘积: xp2r-1=(x-1)Φ1(x)Φ2(x)…Φ2r(x), 其中 Φi(x)=xpi-1(p-1)+xpi-1(p-2)+…+ xpi-1+1, 1≤i≤2r。 而序列(eu)的极小多项式为xp2r-1的一个因子。下面通过寻找能被(eu)满足的F2上的线性递推关系式,决定这个极小多项式。 由性质1知,当gcd(u,p)=1时,有 Hr(u+kp2r-1)≡Hr(u)+ kλuχ-1pr-1(modpr), 要计算χkuχ-1pr-1模pr的值,只需考虑χkuχ-1模p的值。因为 {χkuχ-1(modp)∶k=0,1,…,p-1}= {0,1,…,p-1}, 所以 {Hr(u+kp2r-1)∶k=0,1,…,p-1}= {Hr(u),Hr(u)+pr-1,…,Hr(u)+(p-1)pr-1}。 当k遍历集合{0,1,…,p-1}时,存在(p+1)/2个整数k,使得eu+kp2r-1=0,且有(p-1)/2个整数k,使得eu+kp2r-1=1,其中,0≤k≤p-1。当gcd(u,p)=1时,恒有: eu+eu+p2r-1+eu+(p-1)p2r-1=(p-1)/2。 当gcd(u,p)>1时,由Hr(u)的定义知: eu+eu+p2r-1+…+eu+kp2r-1=0。 于是,当且仅当p≡1(mod 4)时,对所有整数u,恒有以下线性递推关系: eu+eu+p2r-1+…+eu+(p-1)p2r-1=0。 其对应特征多项式为: Φ2r(x)=xp2r-1(p-1)+ xp2r-1(p-2)+…+xp2r-1+1。 因为它是即可约多项式,所以它就是序列(eu)的极小多项式。此时,(eu)的线性复杂度为: LC(eu)=(p-1)p2r-1。 当p≡3(mod 4)时,上述递推关系不成立。 但当p≡3(mod 4)时,对所有的整数u都有: e0+epr+…+e(pr-1)pr+ 从而序列(eu)对应的特征多项式为:xp2r-1+…+x+1,正好是即可约多项式Φ1(x)Φ2(x)…Φ2r(x)的积,即为序列(eu)的极小多项式;此时序列(eu)线性复杂度为LC(eu)=p2r-1。 本文利用广义欧拉商构造了一类伪随机二元序列,通过线性递归关系确定了序列的线性复杂度。这类序列的线性复杂度均大于周期p2r的1/2,尤其当p≡3(mod 4)时,序列的线性复杂度为p2r-1。2 广义欧拉商的定义
3 广义欧拉商的性质

4 基于广义欧拉商的二元序列
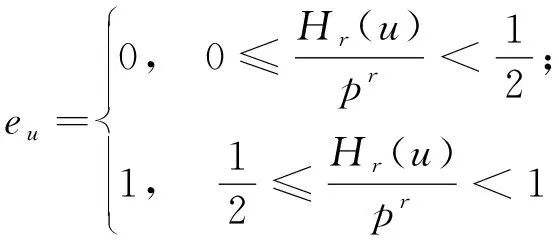
5 结 论
